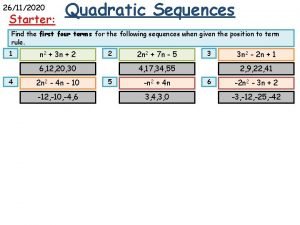
Sequences Linear Quadratic Demonstration This resource provides animated

Sequences – Linear & Quadratic – Demonstration This resource provides animated demonstrations of the mathematical method. Check animations and delete slides not needed for your class.

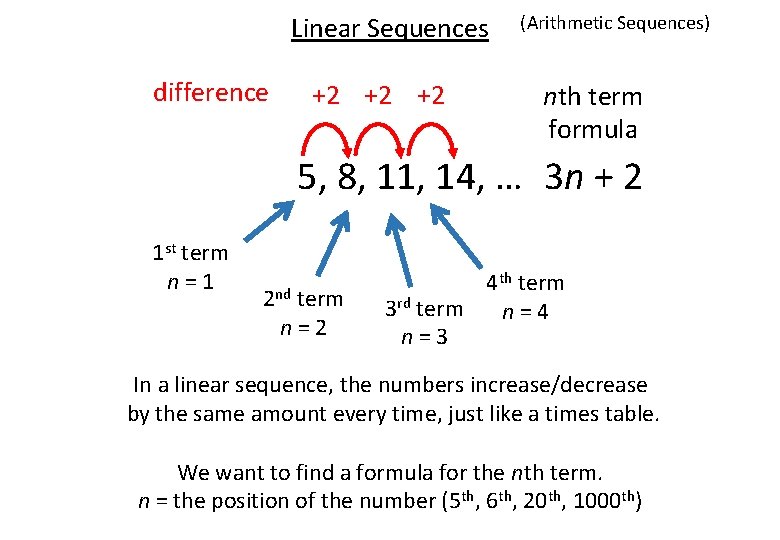
Linear Sequences difference +2 +2 +2 (Arithmetic Sequences) nth term formula 5, 8, 11, 14, … 3 n + 2 1 st term n=1 2 nd term n=2 4 th term 3 rd term n=4 n=3 In a linear sequence, the numbers increase/decrease by the same amount every time, just like a times table. We want to find a formula for the nth term. n = the position of the number (5 th, 6 th, 20 th, 1000 th)

Example 1 +2 +2 +2 +3 5, 7, 9, 11, … 2 4 6 8 1) What times table is hidden in the sequence? 2) What do we need to add/subtract to make the sequences match? nth term formula = (2 × n) + 3 = 2 n + 3 CHECK! n = 4 4 th = (2 × 4) + 3 = 11

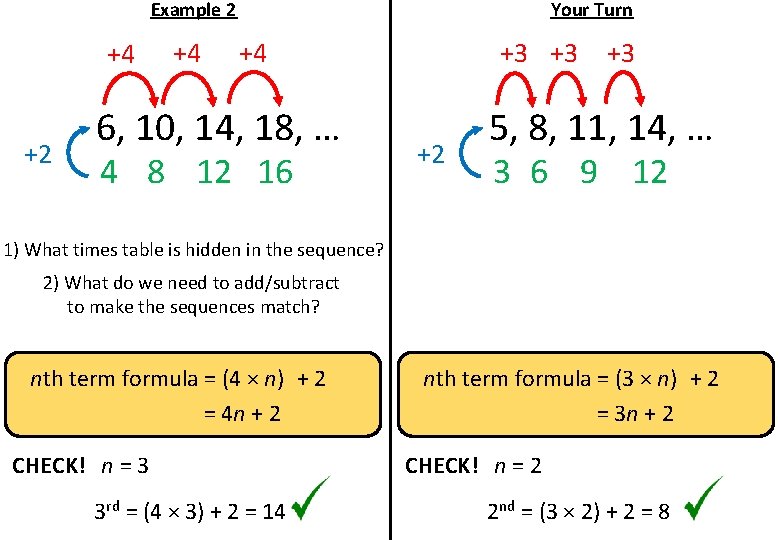
Example 2 +4 +4 6, 10, 14, 18, … 4 8 12 16 1) What times table is hidden in the sequence? 2) What do we need to add/subtract to make the sequences match? nth term formula = (4 × n) + 2 = 4 n + 2 CHECK! n = 3 3 rd = (4 × 3) + 2 = 14

Example 2 +4 +2 +4 Your Turn +4 6, 10, 14, 18, … 4 8 12 16 +3 +3 +2 +3 5, 8, 11, 14, … 3 6 9 12 1) What times table is hidden in the sequence? 2) What do we need to add/subtract to make the sequences match? nth term formula = (4 × n) + 2 = 4 n + 2 CHECK! n = 3 3 rd = (4 × 3) + 2 = 14 nth term formula = (3 × n) + 2 = 3 n + 2 CHECK! n = 2 2 nd = (3 × 2) + 2 = 8

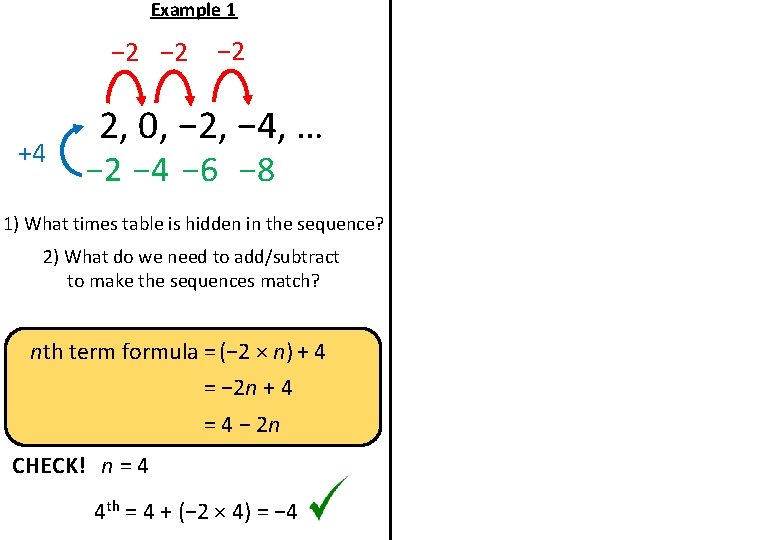
Example 1 − 2 +4 − 2 2, 0, − 2, − 4, … − 2 − 4 − 6 − 8 1) What times table is hidden in the sequence? 2) What do we need to add/subtract to make the sequences match? nth term formula = (− 2 × n) + 4 = − 2 n + 4 = 4 − 2 n CHECK! n = 4 4 th = 4 + (− 2 × 4) = − 4

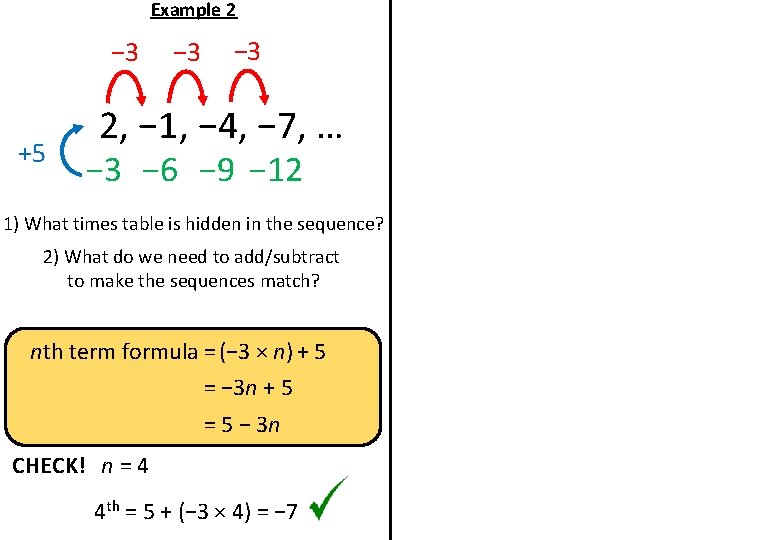
Example 2 − 3 +5 − 3 2, − 1, − 4, − 7, … − 3 − 6 − 9 − 12 1) What times table is hidden in the sequence? 2) What do we need to add/subtract to make the sequences match? nth term formula = (− 3 × n) + 5 = − 3 n + 5 = 5 − 3 n CHECK! n = 4 4 th = 5 + (− 3 × 4) = − 7

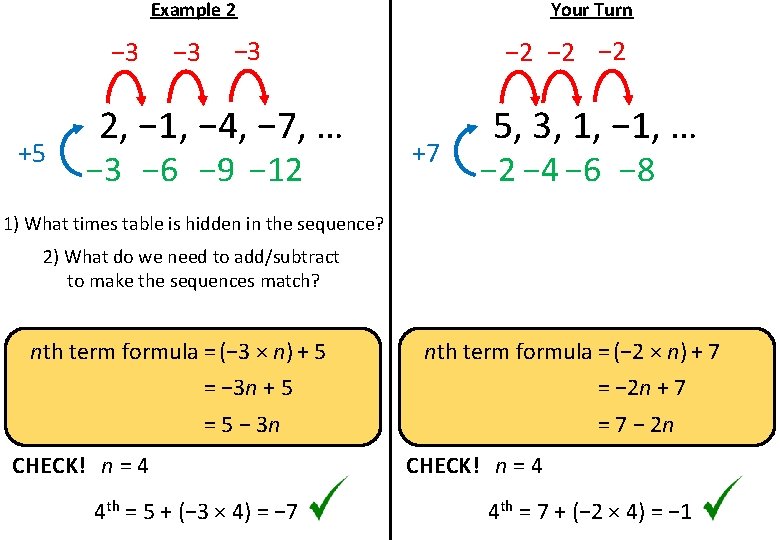
Example 2 − 3 +5 − 3 Your Turn − 3 2, − 1, − 4, − 7, … − 3 − 6 − 9 − 12 − 2 − 2 +7 5, 3, 1, − 1, … − 2 − 4 − 6 − 8 1) What times table is hidden in the sequence? 2) What do we need to add/subtract to make the sequences match? nth term formula = (− 3 × n) + 5 = − 3 n + 5 nth term formula = (− 2 × n) + 7 = − 2 n + 7 = 5 − 3 n CHECK! n = 4 4 th = 5 + (− 3 × 4) = − 7 = 7 − 2 n CHECK! n = 4 4 th = 7 + (− 2 × 4) = − 1

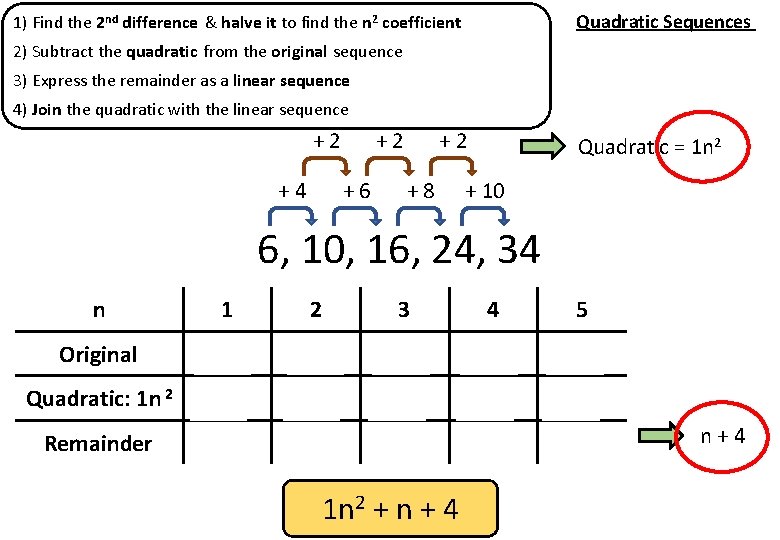
Quadratic Sequences 1) Find the 2 nd difference & halve it to find the n 2 coefficient 2) Subtract the quadratic from the original sequence 3) Express the remainder as a linear sequence 4) Join the quadratic with the linear sequence +2 +4 +2 +6 +2 +8 Quadratic = 1 n 2 + 10 96, 10, 16, 24, 34 n 1 2 3 4 5 Original 6 10 16 24 34 Quadratic: 1 n 2 1 4 9 16 25 Remainder 5 6 7 8 9 1 n 2 + n + 4 n+4

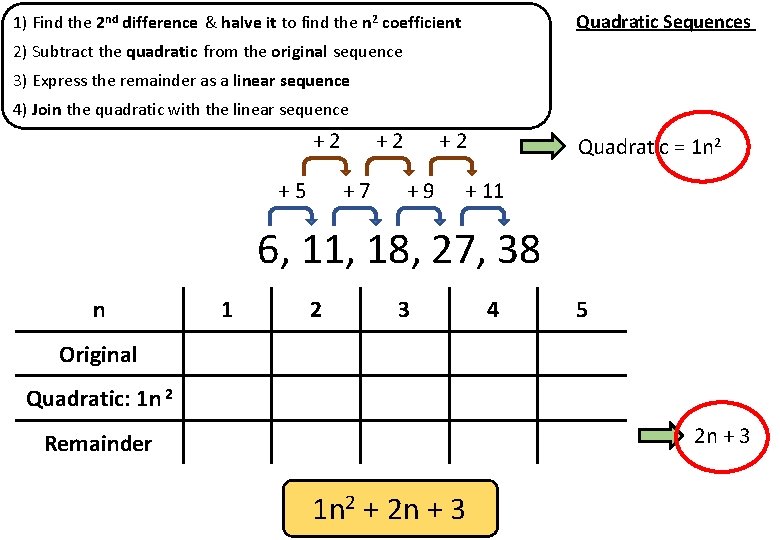
Quadratic Sequences 1) Find the 2 nd difference & halve it to find the n 2 coefficient 2) Subtract the quadratic from the original sequence 3) Express the remainder as a linear sequence 4) Join the quadratic with the linear sequence +2 +5 +2 +7 +2 +9 Quadratic = 1 n 2 + 11 96, 11, 18, 27, 38 n 1 2 3 4 5 Original 6 11 18 27 38 Quadratic: 1 n 2 1 4 9 16 25 Remainder 5 7 9 11 13 1 n 2 + 2 n + 3

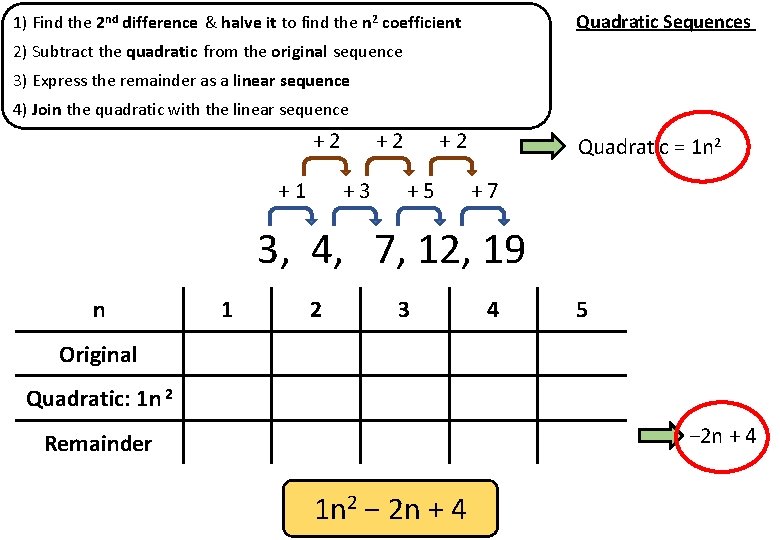
Quadratic Sequences 1) Find the 2 nd difference & halve it to find the n 2 coefficient 2) Subtract the quadratic from the original sequence 3) Express the remainder as a linear sequence 4) Join the quadratic with the linear sequence +2 +1 +2 +3 +2 +5 Quadratic = 1 n 2 +7 93, 4, 7, 12, 19 n 1 2 3 4 5 Original 3 4 7 12 19 Quadratic: 1 n 2 1 4 9 16 25 Remainder 2 0 − 2 − 4 − 6 1 n 2 − 2 n + 4

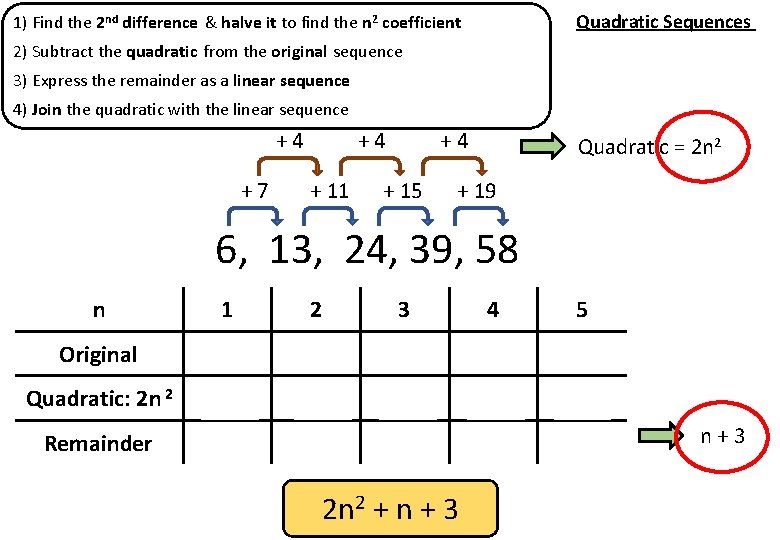
Quadratic Sequences 1) Find the 2 nd difference & halve it to find the n 2 coefficient 2) Subtract the quadratic from the original sequence 3) Express the remainder as a linear sequence 4) Join the quadratic with the linear sequence +4 +7 +4 + 11 +4 + 15 Quadratic = 2 n 2 + 19 96, 13, 24, 39, 58 n 1 2 3 4 5 Original 6 13 24 39 58 Quadratic: 2 n 2 2 8 18 32 50 Remainder 4 5 6 7 8 2 n 2 + n + 3 n+3

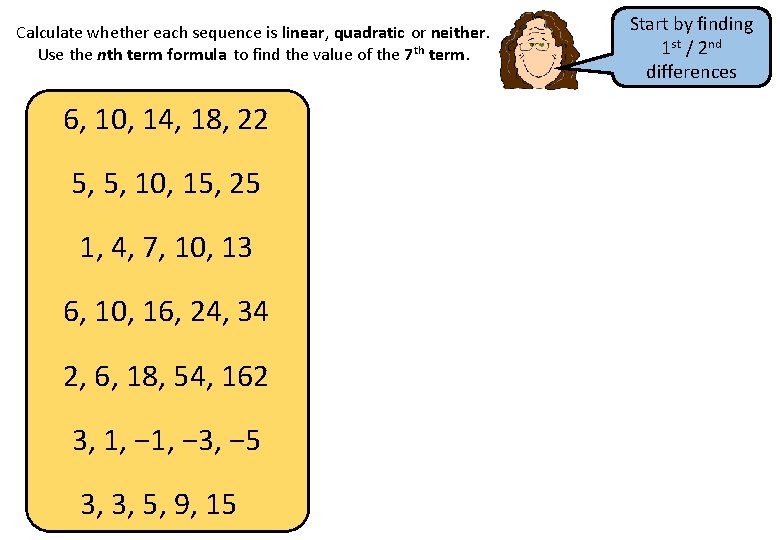
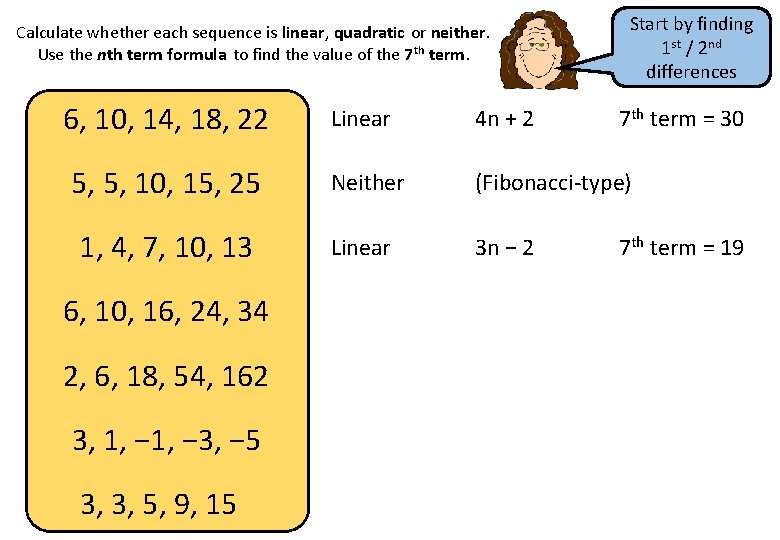
Calculate whether each sequence is linear, quadratic or neither. Use the nth term formula to find the value of the 7 th term. 6, 10, 14, 18, 22 5, 5, 10, 15, 25 1, 4, 7, 10, 13 6, 10, 16, 24, 34 2, 6, 18, 54, 162 3, 1, − 3, − 5 3, 3, 5, 9, 15 Start by finding 1 st / 2 nd differences

Calculate whether each sequence is linear, quadratic or neither. Use the nth term formula to find the value of the 7 th term. Start by finding 1 st / 2 nd differences 6, 10, 14, 18, 22 Linear 4 n + 2 5, 5, 10, 15, 25 Neither (Fibonacci-type) 1, 4, 7, 10, 13 Linear 3 n − 2 6, 10, 16, 24, 34 2, 6, 18, 54, 162 3, 1, − 3, − 5 3, 3, 5, 9, 15 7 th term = 30 7 th term = 19

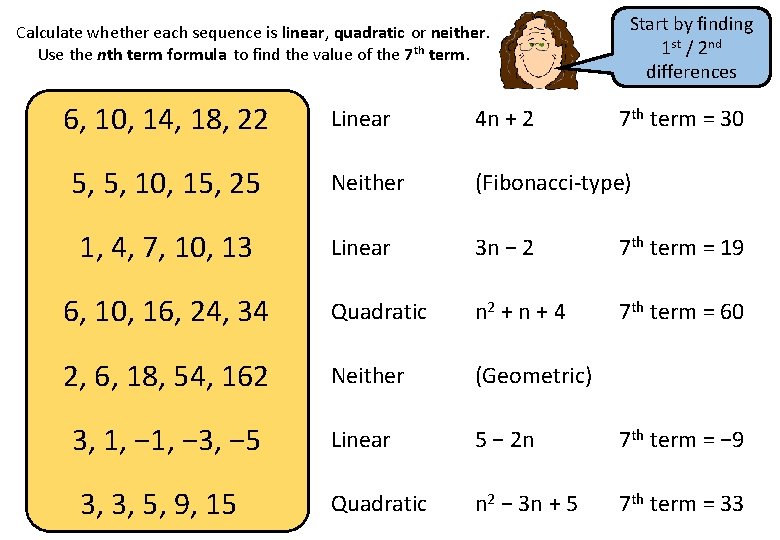
Calculate whether each sequence is linear, quadratic or neither. Use the nth term formula to find the value of the 7 th term. Start by finding 1 st / 2 nd differences 6, 10, 14, 18, 22 Linear 4 n + 2 5, 5, 10, 15, 25 Neither (Fibonacci-type) 1, 4, 7, 10, 13 Linear 3 n − 2 7 th term = 19 6, 10, 16, 24, 34 Quadratic n 2 + n + 4 7 th term = 60 2, 6, 18, 54, 162 Neither (Geometric) 3, 1, − 3, − 5 Linear 5 − 2 n 7 th term = − 9 Quadratic n 2 − 3 n + 5 7 th term = 33 3, 3, 5, 9, 15 7 th term = 30

Questions? Comments? Suggestions? …or have you found a mistake!? Any feedback would be appreciated . Please feel free to email: tom@goteachmaths. co. uk