KS 4 Mathematics A 7 Sequences 1 of

KS 4 Mathematics A 7 Sequences 1 of 68 © Boardworks Ltd 2005

Contents A 7 Sequences A A 7. 1 Generating sequences from rules A A 7. 2 Linear sequences A A 7. 3 Quadratic sequences A A 7. 4 Geometric sequences A A 7. 5 Other types of sequence 2 of 68 © Boardworks Ltd 2005

Sequences In mathematics, a sequence is a succession of numbers that follow a given rule. Each number in a sequence is called a term. For example, 2, 5, 1 st term 8, 11, 14, 17, 20, 23, . . . 6 th term If terms are next to each other they are referred to as consecutive terms. 3 of 68 © Boardworks Ltd 2005

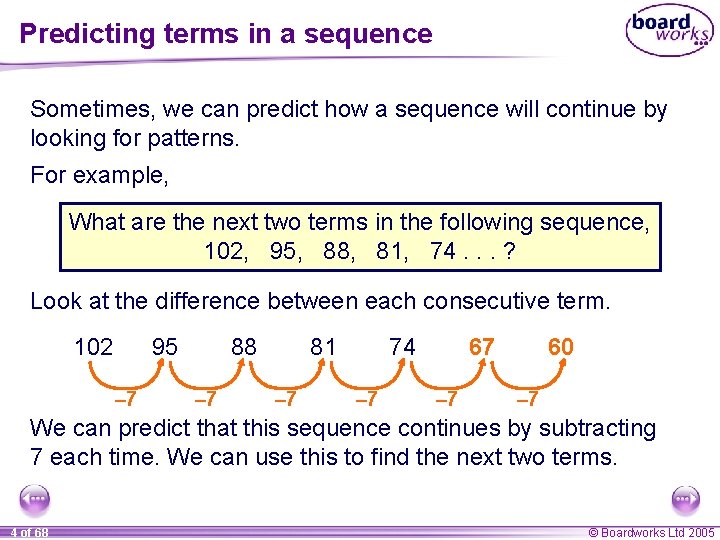
Predicting terms in a sequence Sometimes, we can predict how a sequence will continue by looking for patterns. For example, What are the next two terms in the following sequence, 102, 95, 88, 81, 74. . . ? Look at the difference between each consecutive term. 102 95 – 7 88 – 7 81 – 7 74 – 7 67 – 7 60 – 7 We can predict that this sequence continues by subtracting 7 each time. We can use this to find the next two terms. 4 of 68 © Boardworks Ltd 2005

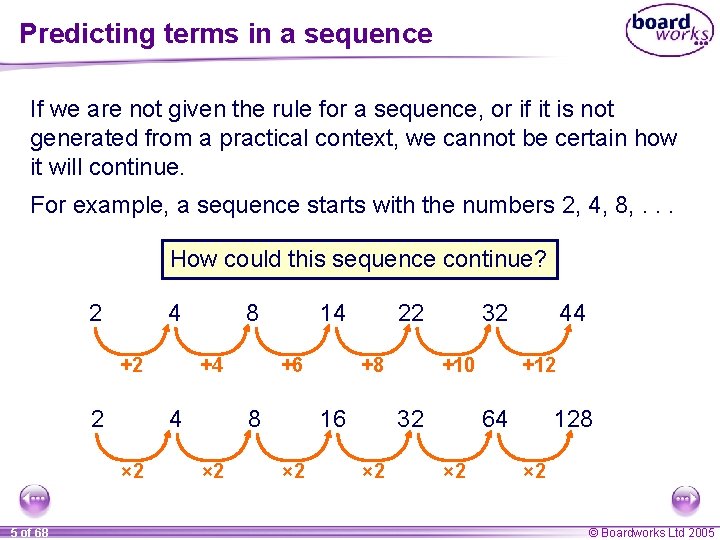
Predicting terms in a sequence If we are not given the rule for a sequence, or if it is not generated from a practical context, we cannot be certain how it will continue. For example, a sequence starts with the numbers 2, 4, 8, . . . How could this sequence continue? 2 4 +2 2 +4 4 × 2 5 of 68 8 14 +6 +8 16 8 × 2 22 × 2 32 +10 32 × 2 44 +12 64 × 2 128 × 2 © Boardworks Ltd 2005

Defining sequences There are two ways to define a sequence. The first is to use a term-to-term rule. To define a sequence using a term-to-term rule we need to know the first term in the sequence and what must be done to each term to give the value of the next term. The second is to use a position-to-term rule. To define a sequence using a position-to-term rule we use a formula for the nth term of the sequence. Term-to-term rules are usually easier to find for a given sequence. Position-to-term rules are harder to find for a given sequence but are more useful for finding any term in a sequence. 6 of 68 © Boardworks Ltd 2005

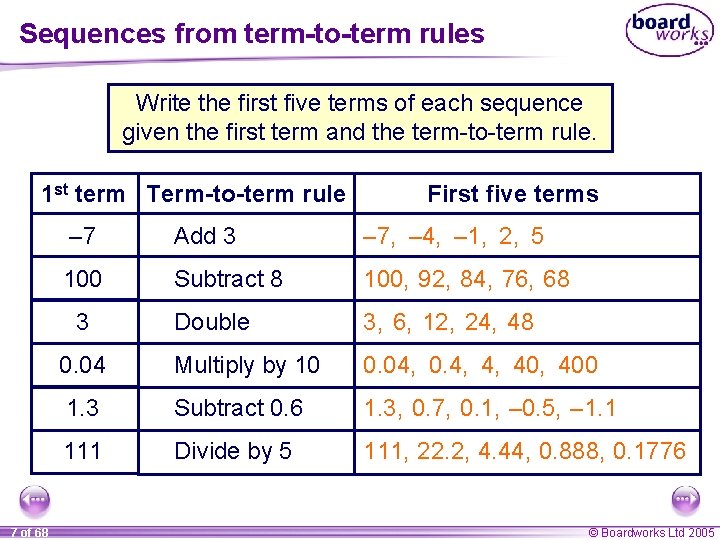
Sequences from term-to-term rules Write the first five terms of each sequence given the first term and the term-to-term rule. 1 st term Term-to-term rule – 7 Add 3 – 7, – 4, – 1, 2, 5 100 Subtract 8 100, 92, 84, 76, 68 Double 3, 6, 12, 24, 48 0. 04 Multiply by 10 0. 04, 0. 4, 4, 400 1. 3 Subtract 0. 6 1. 3, 0. 7, 0. 1, – 0. 5, – 1. 1 111 Divide by 5 111, 22. 2, 4. 44, 0. 888, 0. 1776 3 7 of 68 First five terms © Boardworks Ltd 2005

Sequences from position-to-term rules When a sequence is defined by a position-to-term rule it can sometimes help to put the terms in a table. For example, The nth term in a sequence is n 2, where n is the term’s position in the sequence. Position 1 st 2 nd 3 rd 4 th 5 th … nth Term 1 4 9 16 25 … n 2 Each term can be found by squaring its position in the sequence. What is the 20 th term in this sequence? 202 = 400 8 of 68 © Boardworks Ltd 2005

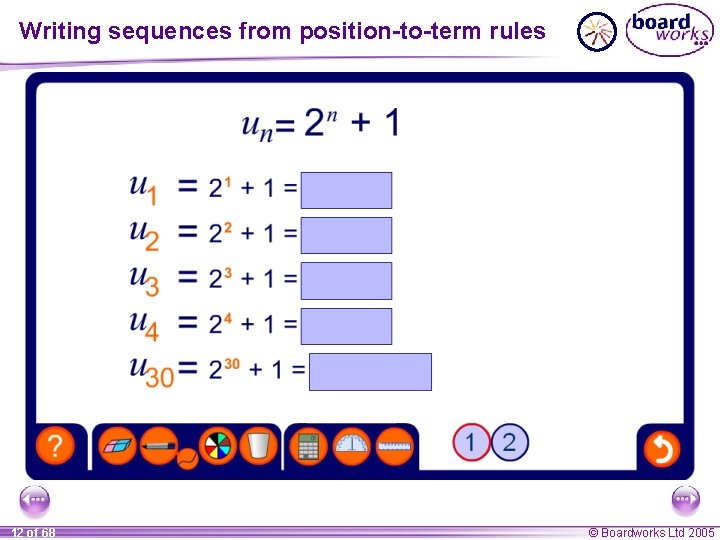
Writing sequences from position-to-term rules The nth term, or the general term, of a sequence is often called un. The 1 st term is then called u 1, the 2 nd term u 2, the 3 rd term u 3, the 4 th term u 4, the 5 th term u 5 and so on. Any term in the sequence can then be found by substituting its position number into the formula for un. 9 of 68 © Boardworks Ltd 2005

Writing sequences from position-to-term rules For example, suppose the nth term of a sequence is 4 n – 5. We can write this rule as: un = 4 n – 5 Find the first five terms in the sequence. u 1 = 4 × 1 – 5 = – 1 u 2 = 4 × 2 – 5 = 3 u 3 = 4 × 3 – 5 = 7 u 4 = 4 × 4 – 5 = 11 u 5 = 4 × 5 – 5 = 15 The first five terms in the sequence are: – 1, 3, 7, 11 and 15. 10 of 68 © Boardworks Ltd 2005

Writing sequences from position-to-term rules The nth term of a sequence is 2 n 2 + 3. We can write this rule as: un = 2 n 2 + 3 Find the first 4 terms in the sequence. u 1 = 2 × 12 + 3 = 5 u 2 = 2 × 22 + 3 = 11 u 3 = 2 × 32 + 3 = 21 u 4 = 2 × 42 + 3 = 35 The first 4 terms in the sequence are: 5, 11, 21, and 35. This sequence is a quadratic sequence. 11 of 68 © Boardworks Ltd 2005

Writing sequences from position-to-term rules 12 of 68 © Boardworks Ltd 2005

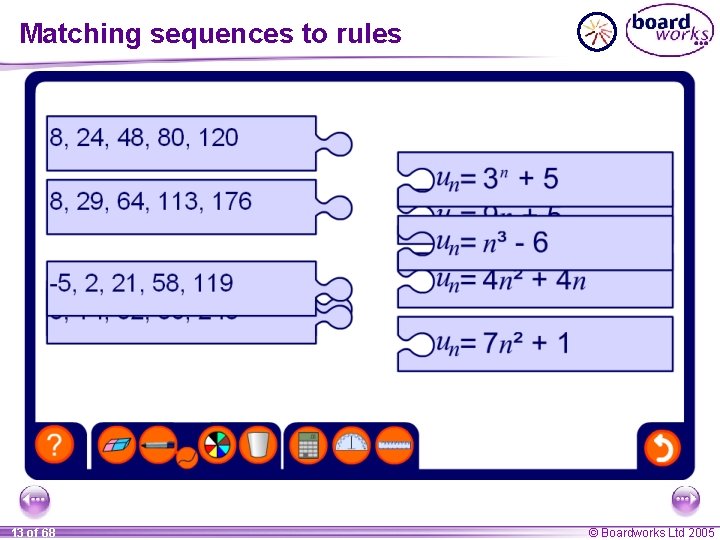
Matching sequences to rules 13 of 68 © Boardworks Ltd 2005

Contents A 7 Sequences A A 7. 1 Generating sequences from rules A A 7. 2 Linear sequences A A 7. 3 Quadratic sequences A A 7. 4 Geometric sequences A A 7. 5 Other types of sequence 14 of 68 © Boardworks Ltd 2005

Sequences that increase in equal steps To work out a rule for a sequence it is often helpful to find the difference between consecutive terms. For example, look at the difference between each term in this sequence: 2, 8, +6 14, +6 20, +6 26, +6 32, +6 38, +6 44, . . . +6 This sequence starts with 2 and increases by adding 6 each time. Every term in this sequence is 4 less than a multiple of 6. 15 of 68 © Boardworks Ltd 2005

Sequences that decrease in equal steps Can you work out the next three terms in this sequence? 10, – 3 7, 4, – 3 1, – 3 – 2, – 3 – 5, – 3 – 8, – 11, . . . – 3 How did you work these out? This sequence starts with 10 and decreases by subtracting 3 from each term to give the next term. When the difference between each term in a sequence is always the same we have a linear or arithmetic sequence. 16 of 68 © Boardworks Ltd 2005

Generating linear sequences When we describe linear sequences we call the constant difference between consecutive terms the common difference, d. We call the first term in a linear sequence a. If we are given the values of a and d in a linear sequence then we can use them to generate the sequence. For example, if a linear sequence has a = 5 and d = – 3, we have the sequence: 5, 2, – 1, – 4, – 7, – 10, . . . Linear sequences can also be generated given the rule for the nth term in the sequence. 17 of 68 © Boardworks Ltd 2005

The nth term of a linear sequence Suppose we are given a linear sequence and asked to find the nth term, un, of the sequence. For example, Find the nth term of the sequence 4, 7, 10, 13, 16, … This sequence continues by adding 3 each time and so the common difference d is 3. We compare the terms in the sequence to the multiples of 3. n 2 3 4 5 Position 1 … × 3 Multiples of 3 3 Term 4 × 3 6 +1 9 +1 7 × 3 12 +1 10 +1 13 × 3 15 +1 16 × 3 3 n +1 … 3 n + 1 un = 3 n + 1. 18 of 68 © Boardworks Ltd 2005

The nth term of a linear sequence Find the nth term of the sequence 5, 3, 1, – 3, … This sequence continues by subtracting 2 each time and so the common difference d is – 2. We compare the terms in the sequence to the multiples of – 2. Position 1 2 × – 2 Multiples of – 2 Term 5 3 × – 2 – 4 +7 × – 2 – 6 +7 3 4 +7 1 5 × – 2 – 8 +7 – 1 … × – 2 – 2 n – 10 +7 – 3 n +7 … 7 – 2 n un = 7 – 2 n. 19 of 68 © Boardworks Ltd 2005

The nth term of a linear sequence If a is the first term of a linear sequence and d is the common difference, we can find the general form of the nth term as follows: u 1 = a, u 2 = a + d, u 3 = a + 2 d, u 4 = a + 3 d, un = a + (n – 1)d, Multiplying out the bracket we have un = a + dn – d. The nth term of a linear sequence with first term a and common difference d is: un = dn + (a – d) 20 of 68 (a – d) is the value of the 0 th term. © Boardworks Ltd 2005

Plotting terms We can also find the nth term of a linear sequence by plotting the value of each given term in the sequence against its position number. For example, The sequence 3, 5, 7, 9, 11 … can be shown graphically: Value of term (un) The points lie on a straight line. Position number (n) 21 of 68 The equation of the line can be written in the form y = mx + c. The value of the gradient m corresponds to the difference between the terms. The value of the y-intercept c corresponds to the 0 th term, to give un = 2 n + 1 © Boardworks Ltd 2005

Finding the nth term of a linear sequence 22 of 68 © Boardworks Ltd 2005

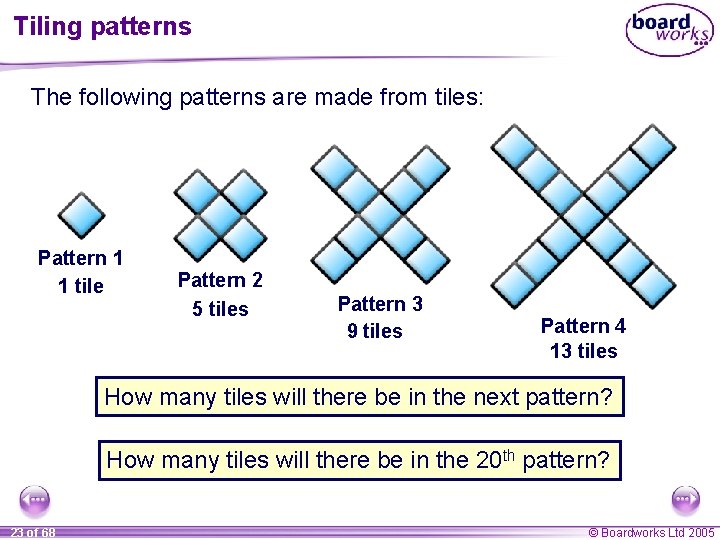
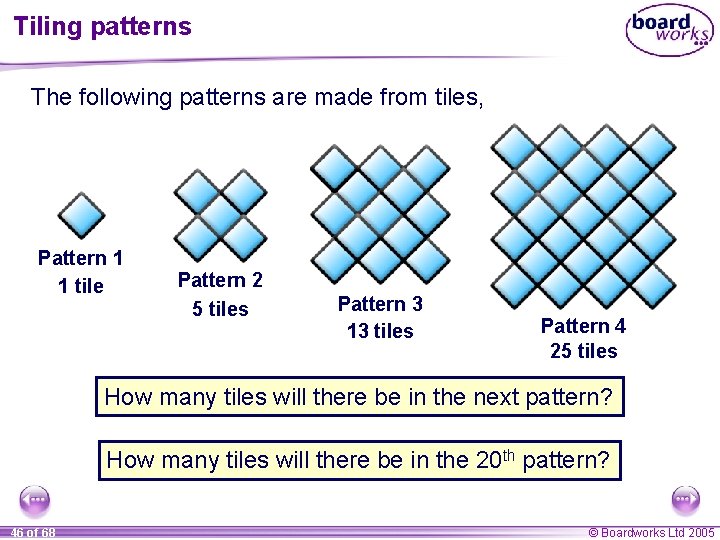
Tiling patterns The following patterns are made from tiles: Pattern 1 1 tile Pattern 2 5 tiles Pattern 3 9 tiles Pattern 4 13 tiles How many tiles will there be in the next pattern? How many tiles will there be in the 20 th pattern? 23 of 68 © Boardworks Ltd 2005

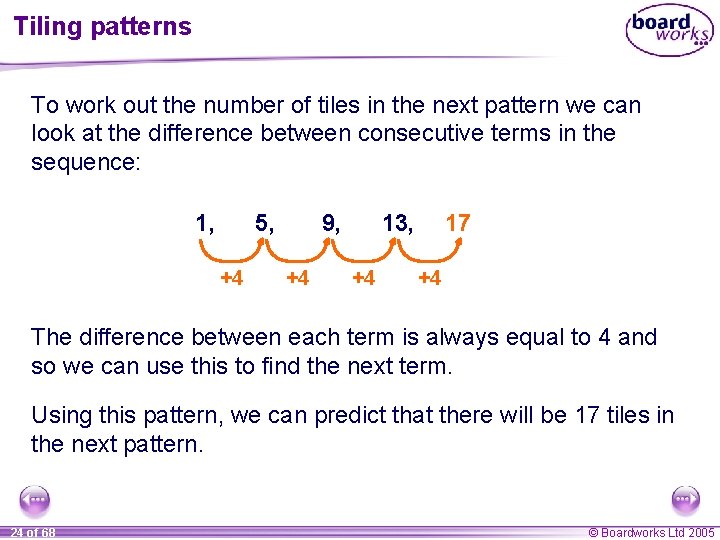
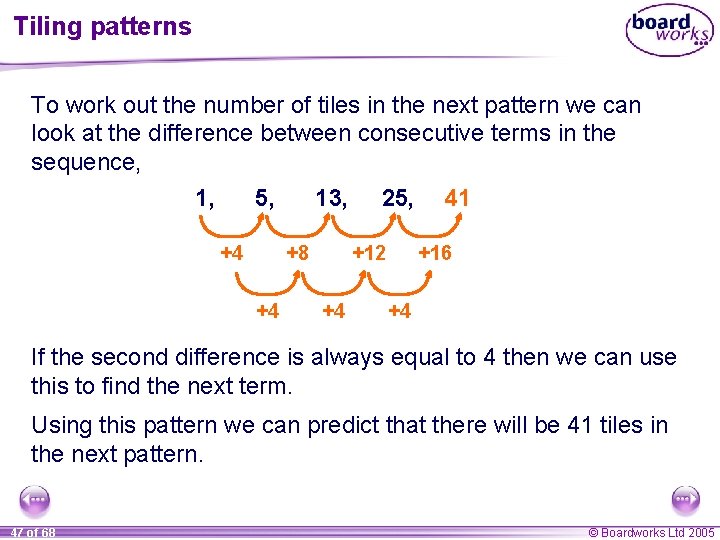
Tiling patterns To work out the number of tiles in the next pattern we can look at the difference between consecutive terms in the sequence: 1, 5, +4 9, +4 13, +4 17 +4 The difference between each term is always equal to 4 and so we can use this to find the next term. Using this pattern, we can predict that there will be 17 tiles in the next pattern. 24 of 68 © Boardworks Ltd 2005

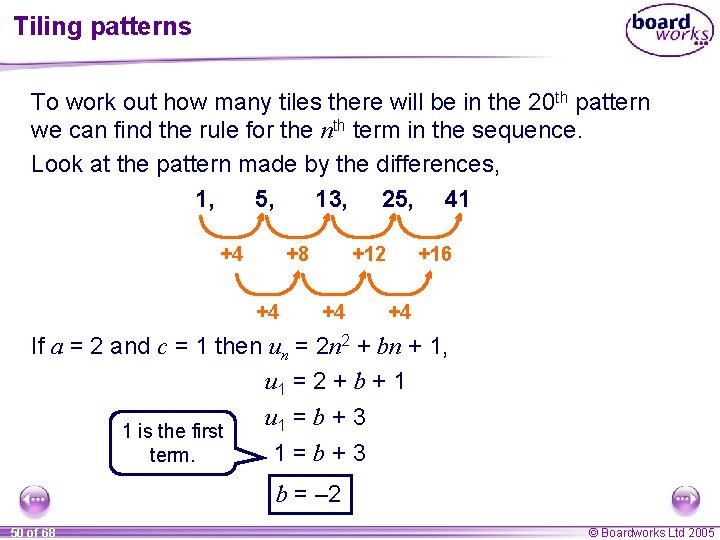
Tiling patterns To work out how many tiles there will be in the 20 th pattern we can find the rule for the nth term in the sequence. Look at the pattern made by the differences: 1, 5, +4 9, +4 13, +4 17 +4 This is a linear sequence and so the nth term will be of the form un = dn + c, where d is the constant difference between the terms. For this sequence the constant difference d = 4. How can we find the value of c? 25 of 68 © Boardworks Ltd 2005

Tiling patterns We can find the rule for the nth term by comparing the sequence to multiples of 4. Position 1 2 × 4 Multiples of 4 4 Term 1 3 × 4 8 – 3 × 4 12 – 3 5 4 – 3 9 5 × 4 16 – 3 13 × 4 20 – 3 17 … n × 4 4 n – 3 … 4 n – 3 un = 4 n – 3. We can use this formula to predict the number of tiles in the 20 th pattern: u 20 = 4 × 20 – 3 = 77 26 of 68 © Boardworks Ltd 2005

Contents A 7 Sequences A A 7. 1 Generating sequences from rules A A 7. 2 Linear sequences A A 7. 3 Quadratic sequences A A 7. 4 Geometric sequences A A 7. 5 Other types of sequence 27 of 68 © Boardworks Ltd 2005

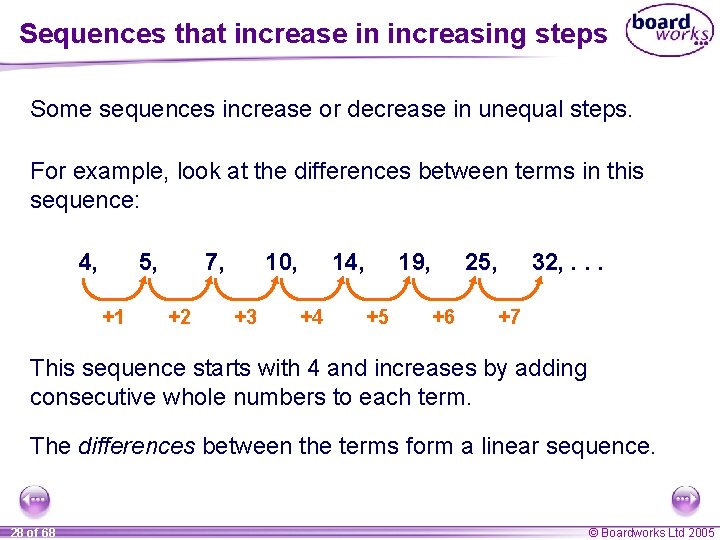
Sequences that increase in increasing steps Some sequences increase or decrease in unequal steps. For example, look at the differences between terms in this sequence: 4, 5, +1 7, +2 10, +3 14, +4 19, +5 25, +6 32, . . . +7 This sequence starts with 4 and increases by adding consecutive whole numbers to each term. The differences between the terms form a linear sequence. 28 of 68 © Boardworks Ltd 2005

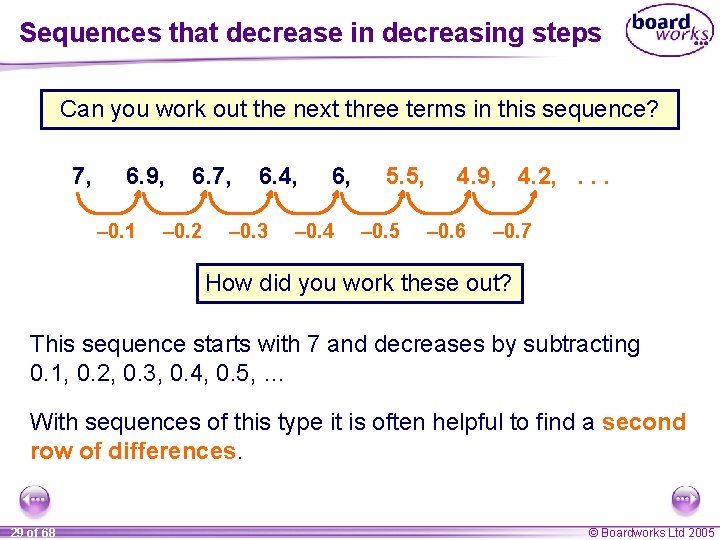
Sequences that decrease in decreasing steps Can you work out the next three terms in this sequence? 7, 6. 9, – 0. 1 6. 7, – 0. 2 6. 4, – 0. 3 6, – 0. 4 5. 5, – 0. 5 4. 9, 4. 2, . . . – 0. 6 – 0. 7 How did you work these out? This sequence starts with 7 and decreases by subtracting 0. 1, 0. 2, 0. 3, 0. 4, 0. 5, … With sequences of this type it is often helpful to find a second row of differences. 29 of 68 © Boardworks Ltd 2005

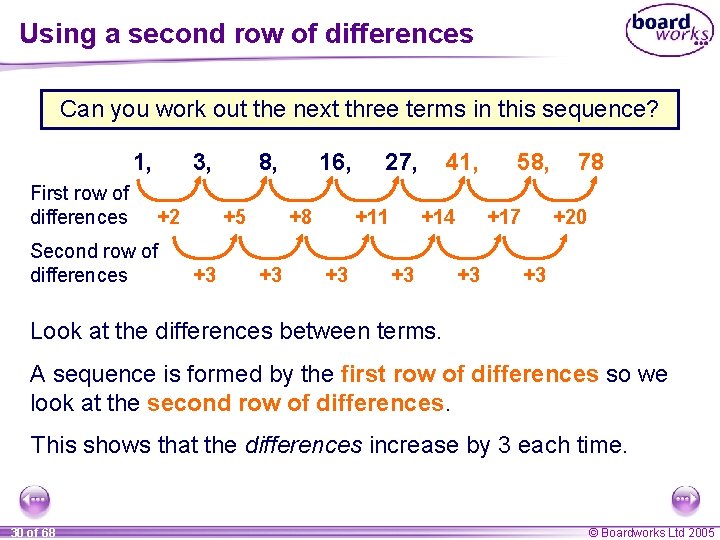
Using a second row of differences Can you work out the next three terms in this sequence? 1, First row of differences 3, +2 Second row of differences 8, +5 +3 16, +8 +3 27, +11 +3 41, +14 +3 58, +17 +3 78 +20 +3 Look at the differences between terms. A sequence is formed by the first row of differences so we look at the second row of differences. This shows that the differences increase by 3 each time. 30 of 68 © Boardworks Ltd 2005

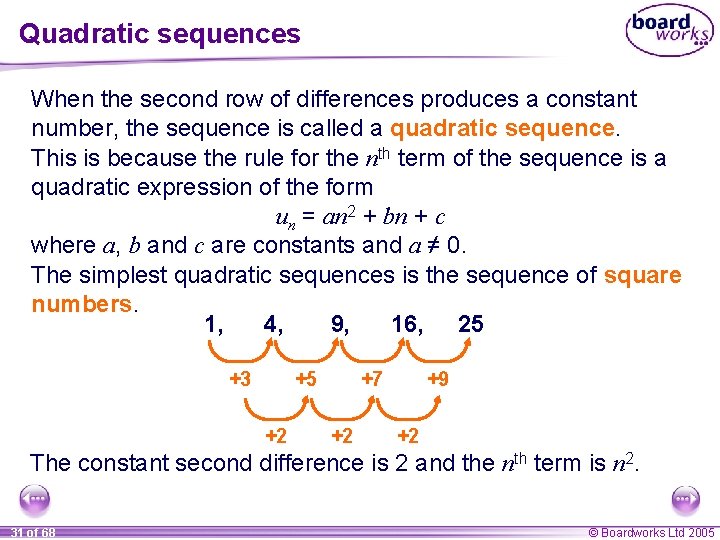
Quadratic sequences When the second row of differences produces a constant number, the sequence is called a quadratic sequence. This is because the rule for the nth term of the sequence is a quadratic expression of the form un = an 2 + bn + c where a, b and c are constants and a ≠ 0. The simplest quadratic sequences is the sequence of square numbers. 1, 4, 9, 16, 25 +3 +5 +2 +7 +2 +9 +2 The constant second difference is 2 and the nth term is n 2. 31 of 68 © Boardworks Ltd 2005

Investigating quadratic sequences 32 of 68 © Boardworks Ltd 2005

The nth term of a quadratic sequence When un = an 2 + bn + c the value of a can be found by halving the value of the second difference, which is always equal to 2 a. We can prove this as follows, un = an 2 + bn + c u 1 = a × 12 + b × 1 + c = a + b + c u 2 = a × 22 + b × 2 + c = 4 a + 2 b + c u 3 = a × 32 + b × 3 + c = 9 a + 3 b + c u 4 = a × 42 + b × 4 + c = 16 a + 4 b + c u 5 = a × 52 + b × 5 + c = 25 a + 5 b + c This gives us the first five terms of a general quadratic sequence. 33 of 68 © Boardworks Ltd 2005

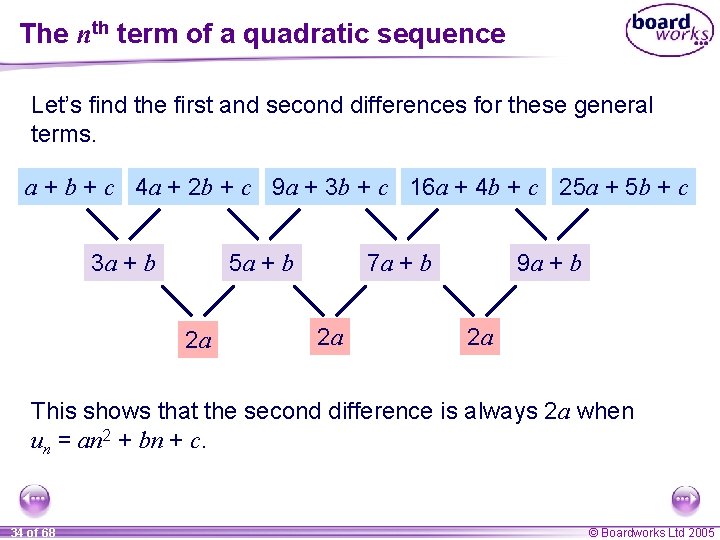
The nth term of a quadratic sequence Let’s find the first and second differences for these general terms. a + b + c 4 a + 2 b + c 9 a + 3 b + c 16 a + 4 b + c 25 a + 5 b + c 3 a + b 5 a + b 2 a 7 a + b 2 a 9 a + b 2 a This shows that the second difference is always 2 a when un = an 2 + bn + c. 34 of 68 © Boardworks Ltd 2005

The nth term of a quadratic sequence When un = an 2 + bn + c the value of c can be found by calculating the value of the 0 th term, u 0. We can prove this as follows, un = an 2 + bn + c u 0 = a × 02 + b × 0 + c u 0 = c Of course, the 0 th term is not really part of the sequence. We can easily work it out though by looking at the sequence formed by the first row of differences and counting back from the first term. 35 of 68 © Boardworks Ltd 2005

The nth term of a quadratic sequence When un = an 2 + bn + c the value of b can be found by subtracting (a + c) from the value of the first term. We can prove this as follows, un = an 2 + bn + c u 1 = a × 12 + b × 1 + c u 1 = a + b + c Rearranging this formula to make b the subject gives, b = u 1 – (a + c) If we find the value of a and c first, we can then use them and the value of the first term, to find b. 36 of 68 © Boardworks Ltd 2005

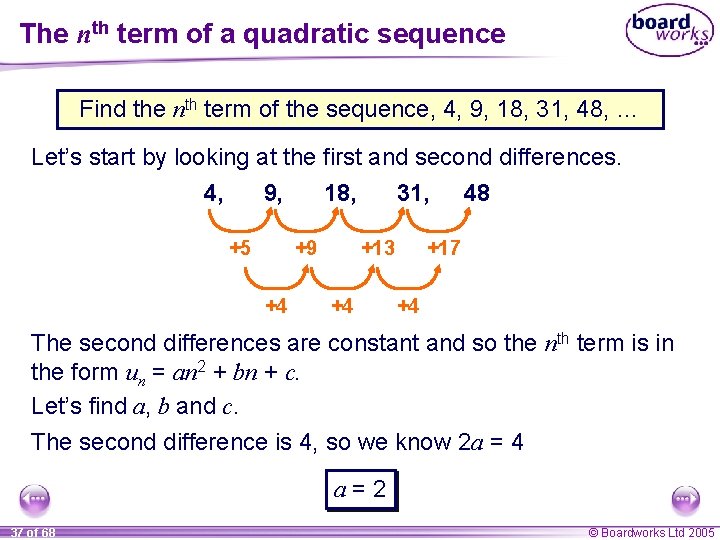
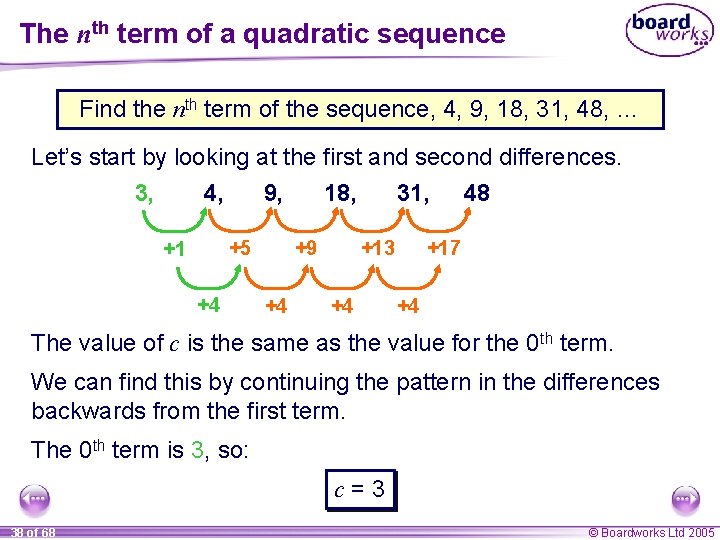
The nth term of a quadratic sequence Find the nth term of the sequence, 4, 9, 18, 31, 48, … Let’s start by looking at the first and second differences. 4, 9, 18, 31, 48 +5 +9 +4 +13 +4 +17 +4 The second differences are constant and so the nth term is in the form un = an 2 + bn + c. Let’s find a, b and c. The second difference is 4, so we know 2 a = 4 a=2 37 of 68 © Boardworks Ltd 2005

The nth term of a quadratic sequence Find the nth term of the sequence, 4, 9, 18, 31, 48, … Let’s start by looking at the first and second differences. 3, 4, 9, 18, 31, 48 +5 +1 +4 +9 +4 +13 +4 +17 +4 The value of c is the same as the value for the 0 th term. We can find this by continuing the pattern in the differences backwards from the first term. The 0 th term is 3, so: c=3 38 of 68 © Boardworks Ltd 2005

The nth term of a quadratic sequence Find the nth term of the sequence, 4, 9, 18, 31, 48, … Putting a = 2 and c = 3 into un =an 2 + bn + c gives us un = 2 n 2 + bn + 3. We can use this to write an expression for the first term: un = 2 n 2 + bn + 3 u 1 = 2 × 12 + b × 1 + 3 u 1 = 2 + b + 3 u 1 = b + 5 The first term in the sequence is 4, so: 4=b+5 b = – 1 39 of 68 © Boardworks Ltd 2005

The nth term of a quadratic sequence Once we have found the values of a, b, and c we can use them in un = an 2 + bn + c to give the nth term. We have found that for the sequence 4, 9, 18, 31, 48, … a = 2, b = – 1 and c = 3, un = 2 n 2 – n + 3 We can check this rule by substituting a chosen value for n into the formula and making sure that it corresponds to the required term in the sequence. For example, when n = 5 we have, u 5 = 2 × 52 – 5 + 3 = 48 Check the rule for other terms in the sequence. 40 of 68 © Boardworks Ltd 2005

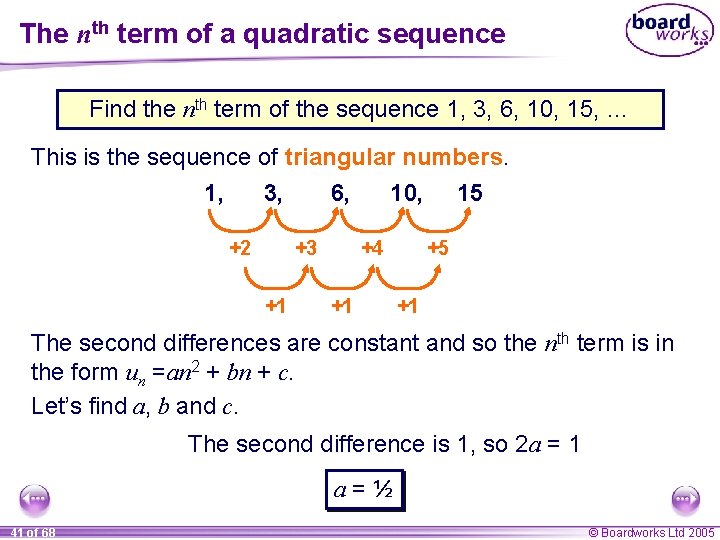
The nth term of a quadratic sequence Find the nth term of the sequence 1, 3, 6, 10, 15, … This is the sequence of triangular numbers. 1, 3, 6, 10, 15 +2 +3 +1 +4 +1 +5 +1 The second differences are constant and so the nth term is in the form un =an 2 + bn + c. Let’s find a, b and c. The second difference is 1, so 2 a = 1 a=½ 41 of 68 © Boardworks Ltd 2005

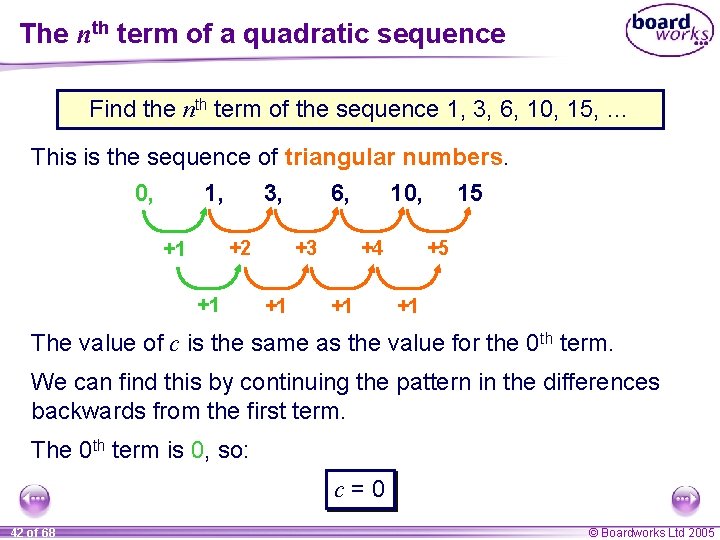
The nth term of a quadratic sequence Find the nth term of the sequence 1, 3, 6, 10, 15, … This is the sequence of triangular numbers. 0, 1, 3, 6, 10, 15 +2 +1 +1 +3 +1 +4 +1 +5 +1 The value of c is the same as the value for the 0 th term. We can find this by continuing the pattern in the differences backwards from the first term. The 0 th term is 0, so: c=0 42 of 68 © Boardworks Ltd 2005

The nth term of a quadratic sequence Find the nth term of the sequence 1, 3, 6, 10, 15, … Putting a = ½ and c = 0 into un =an 2 + bn + c gives us un = ½n 2 + bn. We can use this to write an expression for the first term: un = ½n 2 + bn u 1 = ½ × 12 + b × 1 u 1 = ½ + b The first term in the sequence is 1, so 1=½+b b=½ 43 of 68 © Boardworks Ltd 2005

The nth term of a quadratic sequence Once we have found the values of a, b, and c we can use them in an 2 + bn + c to give the nth term. We have found that for the sequence 1, 3, 6, 10, 15, … a = ½, b = ½ and c = 0; n 2 n un = + 2 2 or n 2 + n un = 2 Checking, when n = 5, we have u 5 = ½(52 + 5) = 15 Check the rule for other terms in the sequence. 44 of 68 © Boardworks Ltd 2005

Finding the nth term of a quadratic sequence 45 of 68 © Boardworks Ltd 2005

Tiling patterns The following patterns are made from tiles, Pattern 1 1 tile Pattern 2 5 tiles Pattern 3 13 tiles Pattern 4 25 tiles How many tiles will there be in the next pattern? How many tiles will there be in the 20 th pattern? 46 of 68 © Boardworks Ltd 2005

Tiling patterns To work out the number of tiles in the next pattern we can look at the difference between consecutive terms in the sequence, 1, 5, 13, 25, 41 +4 +8 +4 +12 +4 +16 +4 If the second difference is always equal to 4 then we can use this to find the next term. Using this pattern we can predict that there will be 41 tiles in the next pattern. 47 of 68 © Boardworks Ltd 2005

Tiling patterns To work out how many tiles there will be in the 20 th pattern we can find the rule for the nth term in the sequence. Look at the pattern made by the differences, 1, 5, 13, 25, 41 +4 +8 +4 +12 +4 +16 +4 The second difference is constant and so the nth term will be a quadratic of the form un = an 2 + bn + c. The second difference is always equal to 2 a: 2 a = 4 a=2 48 of 68 © Boardworks Ltd 2005

Tiling patterns To work out how many tiles there will be in the 20 th pattern we can find the rule for the nth term in the sequence. Look at the pattern made by the differences, 1, 1, 5, 13, 25, 41 +0 +4 +4 +8 +4 +12 +4 +16 +4 The value of c is equal to the 0 th term. The 0 th term is equal to 1, so: c=1 49 of 68 © Boardworks Ltd 2005

Tiling patterns To work out how many tiles there will be in the 20 th pattern we can find the rule for the nth term in the sequence. Look at the pattern made by the differences, 1, 5, 13, 25, 41 +4 +8 +4 +12 +4 +16 +4 If a = 2 and c = 1 then un = 2 n 2 + bn + 1, u 1 = 2 + b + 1 u 1 = b + 3 1 is the first 1=b+3 term. b = – 2 50 of 68 © Boardworks Ltd 2005

Tiling patterns We can now substitute a=2 b = – 2 c=1 into the general form for the nth term of the quadratic sequence, an 2 + bn + c, to give us the following rule for the nth term: un = 2 n 2 – 2 n + 1 We can now use this formula to find the value of the 20 th term. u 20 = 2 × 202 – 2 × 20 + 1 = 800 – 40 + 1 = 761 We can predict that there will be 761 tiles in the 20 th pattern. 51 of 68 © Boardworks Ltd 2005

Contents A 7 Sequences A A 7. 1 Generating sequences from rules A A 7. 2 Linear sequences A A 7. 3 Quadratic sequences A A 7. 4 Geometric sequences A A 7. 5 Other types of sequence 52 of 68 © Boardworks Ltd 2005

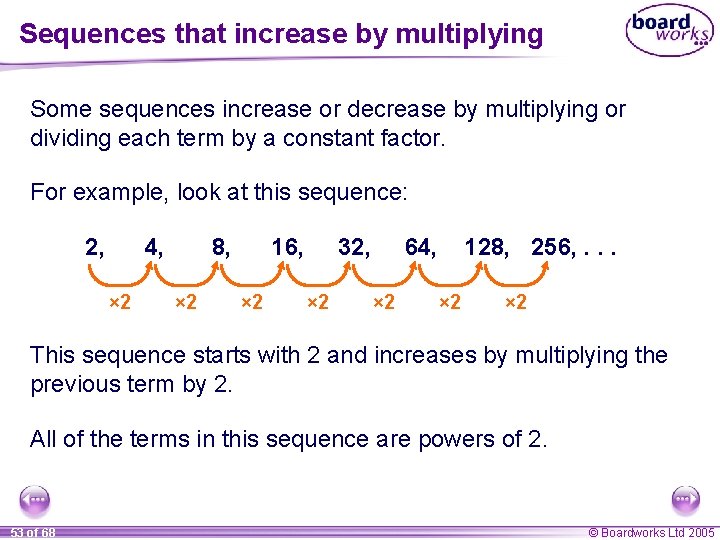
Sequences that increase by multiplying Some sequences increase or decrease by multiplying or dividing each term by a constant factor. For example, look at this sequence: 2, 4, × 2 8, × 2 16, × 2 32, × 2 64, × 2 128, 256, . . . × 2 This sequence starts with 2 and increases by multiplying the previous term by 2. All of the terms in this sequence are powers of 2. 53 of 68 © Boardworks Ltd 2005

Sequences that decrease by dividing Can you work out the next three terms in this sequence? 1024, 256, ÷ 4 64, 16, ÷ 4 4, ÷ 4 1, ÷ 4 , 1 , 16 . . . ÷ 4 How did you work these out? This sequence starts with 1024 and decreases by dividing by 4 each time. We could also continue this sequence by multiplying each term by 14 to give the next term. 54 of 68 © Boardworks Ltd 2005

Geometric sequences Sequences that go from one term to the next by multiplying by a constant amount are called geometric sequences. The amount that each term is multiplied by to get the next term is called the common ratio of the sequence. The common ratio r of a geometric sequence can be found by dividing any term in the sequence by the one before it. For example, Find the common ratio for the following geometric sequence: 8, 12, 18, 27, 40. 5, … r = 12 ÷ 8 = 1. 5 The sequence continues by multiplying the previous term by 1. 5. 55 of 68 © Boardworks Ltd 2005

Continuing geometric sequences 56 of 68 © Boardworks Ltd 2005

The nth term of a geometric sequence Suppose we are given a geometric sequence and asked to find the nth term un of the sequence. For example: Find the nth term of the sequence, 3, 6, 12, 24, 48, … The first term of this sequence is 3 and it continues by multiplying the previous term by 2 each time. We can write this sequence as follows: u 1 = 3 u 2 = 6 = 3 × 2 u 3 = 12 = 3 × 22 u 4 = 24 = 3 × 2 × 2 = 3 × 23 u 5 = 24 = 3 × 2 × 2 = 3 × 24 un = 3 × 2(n – 1) 57 of 68 © Boardworks Ltd 2005

The nth term of a geometric sequence In general, if the first term of a geometric sequence is a and the common ratio is r, then we can find the general form of the nth term as follows: u 1 = a, u 2 = a × r, u 3 = a × r 2, u 4 = a × r 3, u 5 = a × r 4, un = a × rn – 1, The nth term of a geometric sequence with first term a and common ratio r is un = arn – 1 58 of 68 © Boardworks Ltd 2005

Geometric sequences in real-life Geometric sequences often occur in real-life situations where there is a repeated percentage change. For example, £ 800 is invested in an account with an annual interest rate of 5%. Write a formula for the value of the investment at the beginning of the nth year. Every year the amount in the account is multiplied by 1. 05. The amount in the account at the beginning of each year forms a geometric sequence with £ 800 as the first term and 1. 05 as the common ratio. £ 800, £ 840, £ 882, £ 926. 10, … × 1. 05 59 of 68 × 1. 05 © Boardworks Ltd 2005

Geometric sequences in real-life Geometric sequences often occur in real-life situations where there is a repeated percentage change. For example, £ 800 is invested in an account with an annual interest rate of 5%. Write a formula for the value of the investment at the beginning of the nth year. We can write the sequence as, u 1 = £ 800 u 2 = £ 800 × 1. 05 u 3 = £ 800 × 1. 052 u 4 = £ 800 × 1. 053 un = £ 800 × 1. 05 n – 1 60 of 68 © Boardworks Ltd 2005

Contents A 7 Sequences A A 7. 1 Generating sequences from rules A A 7. 2 Linear sequences A A 7. 3 Quadratic sequences A A 7. 4 Geometric sequences A A 7. 5 Other types of sequence 61 of 68 © Boardworks Ltd 2005

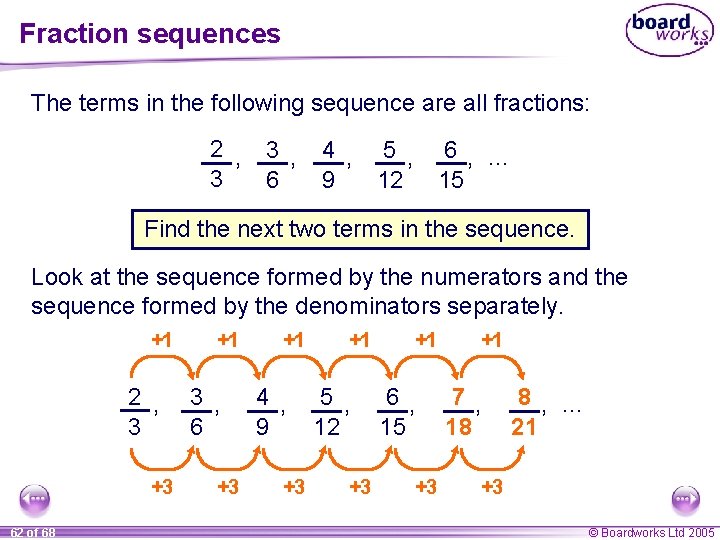
Fraction sequences The terms in the following sequence are all fractions: 2 , 3 3 , 6 4 , 5 , 6, … 9 12 15 Find the next two terms in the sequence. Look at the sequence formed by the numerators and the sequence formed by the denominators separately. +1 2 , 3 +3 62 of 68 +1 3 , 6 +3 +1 4 , 9 +3 +1 5 , 12 +3 +1 6, 15 +3 +1 7, 18 8, … 21 +3 © Boardworks Ltd 2005

Fraction sequences The terms in the following sequence are all fractions, 2 , 3 3 , 6 4 , 5 , 6, … 9 12 15 Find the formula for the nth term of the sequence. The sequence formed by the numerators is: 63 of 68 The sequence formed by the numerators is: u 1 = 2 u 1 = 3 u 2 = 6 u 3 = 4 u 3 = 9 un = n + 1 un = 3 n © Boardworks Ltd 2005

Fraction sequences The terms in the following sequence are all fractions: 2 , 3 3 , 6 4 , 5 , 6, … 9 12 15 Find the formula for the nth term of the sequence. Given that the nth term for the numerators is n + 1 and the nth term for the denominators is 3 n, we can write the formula for the nth term of the above sequence as: n+1 un = 3 n 64 of 68 © Boardworks Ltd 2005

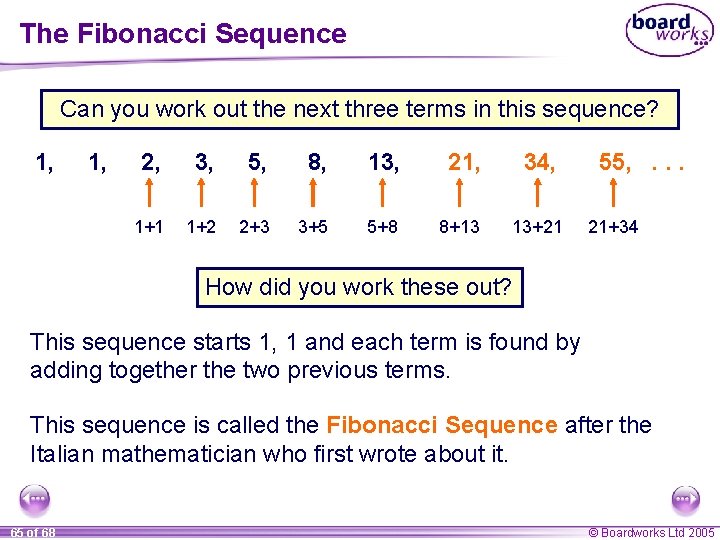
The Fibonacci Sequence Can you work out the next three terms in this sequence? 1, 2, 3, 5, 8, 13, 21, 1+1 1+2 2+3 3+5 5+8 8+13 34, 13+21 55, . . . 21+34 How did you work these out? This sequence starts 1, 1 and each term is found by adding together the two previous terms. This sequence is called the Fibonacci Sequence after the Italian mathematician who first wrote about it. 65 of 68 © Boardworks Ltd 2005

The nth term of the Fibonacci Sequence The Fibonacci Sequence is an example of a sequence for which the general term cannot be written in terms of its position in the sequence. To find any given term we have to know the value of the previous two terms. u 1 = 1 We can write: u 2 = 1 u 3 = u 2 + u 1 u 4 = u 3 + u 2 u 5 = u 4 + u 3 The nth term can then be written as: un = un – 1 + un – 2 66 of 68 © Boardworks Ltd 2005

The nth term of the Fibonacci sequence The formula un = un – 1 + un – 2 is called an iterative formula. The sequence cannot be defined by this formula alone. We have to be given the value of the first two terms. Can you use this formula to find the 100 th term in the sequence? Using this formula would give us, u 100 = u 99 + u 98 All this tells us is that the 100 th term is equal to the sum of the 99 th term and the 98 th term. The only way to find the 100 th term is to use a computer or spend some time doing a lot of arithmetic! 67 of 68 © Boardworks Ltd 2005

Using iterative formulae to generate sequences Write down the first five terms of the sequence generated by the iterative formula un = 2 un – 1 + 1 when u 1 = 3 u 2 = 6 + 1 = 7 u 3 = 14 + 1 = 15 u 4 = 30 + 1 = 31 u 5 = 62 + 1 = 63 The first five terms of the sequence are 3, 7, 15, 31, 63, … Can you find the formula for the nth term of this sequence? 68 of 68 © Boardworks Ltd 2005