Nonlinear Systems Warm Up Solve each quadratic equation


















- Slides: 20

Nonlinear Systems Warm Up Solve each quadratic equation by factoring. Check your answer. 5, -2 -2 Find the number of real solutions of each equation using the discriminant. 3. 25 x 2 - 10 x + 1 = 0 one 1. x 2 - 3 x - 10 = 0 2. -3 x 2 - 12 x = 12 4. 2 x 2 + 7 x + 2 = 0 two 5. 3 x 2 + x + 2 = 0 none Holt Mc. Dougal Algebra 1

Nonlinear Systems Recall that a system of linear equations is a set of two or more linear equations. A solution of a system is an ordered pair that satisfies each equation in the system. Points where the graphs of the equations intersect represent solutions of the system. A nonlinear system of equations is a system in which at least one of the equations is nonlinear. For example, a system that contains one quadratic equation and one linear equation is a nonlinear system. Holt Mc. Dougal Algebra 1

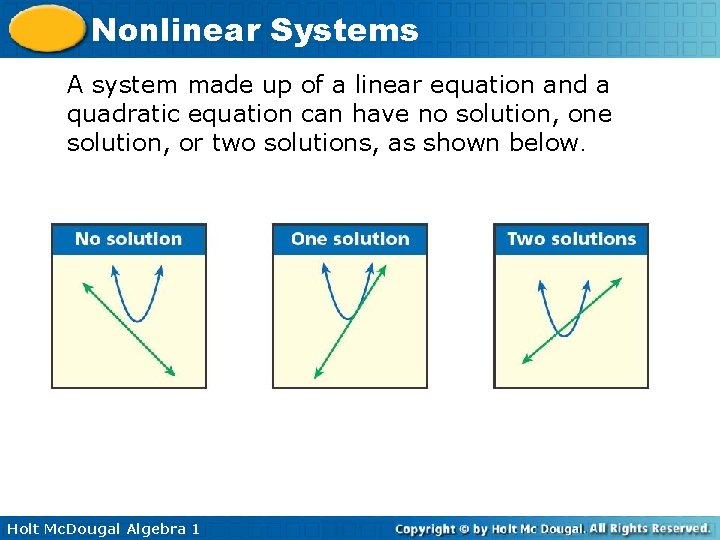
Nonlinear Systems A system made up of a linear equation and a quadratic equation can have no solution, one solution, or two solutions, as shown below. Holt Mc. Dougal Algebra 1

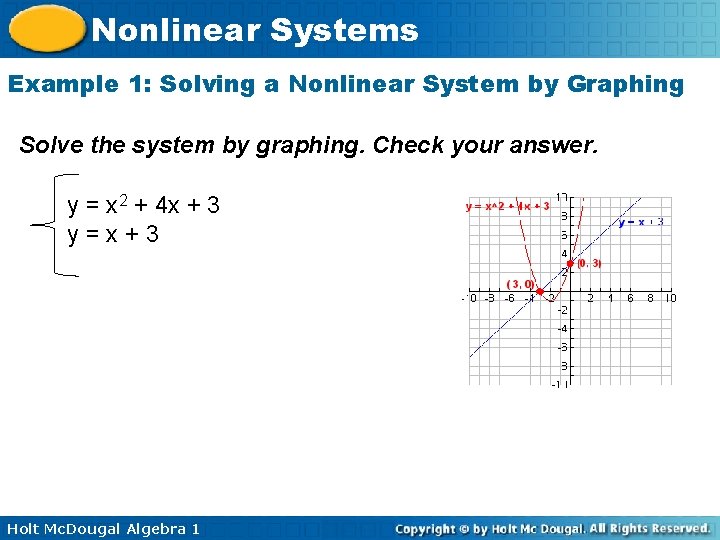
Nonlinear Systems Example 1: Solving a Nonlinear System by Graphing Solve the system by graphing. Check your answer. y = x 2 + 4 x + 3 y=x+3 Holt Mc. Dougal Algebra 1

Nonlinear Systems Check It Out! Example 1 1. Solve the system by graphing. Check your answer. y = x 2 - 4 x + 5 y=x+1 Holt Mc. Dougal Algebra 1

Nonlinear Systems Remember! The substitution method is a good choice when either equation is solved for a variable, both equations are solved for the same variable, or a variable in either equation has a coefficient of 1 or -1. Holt Mc. Dougal Algebra 1

Nonlinear Systems Example 2: Solving a Nonlinear system by substitution. Solve the system by substitution. y = x 2 - x - 5 y = -3 x + 3 Holt Mc. Dougal Algebra 1

Nonlinear Systems Example 2: Continued The solutions are (4, 15) and (2, – 3). Holt Mc. Dougal Algebra 1

Nonlinear Systems Check It Out! Example 2 1. Solve the system by substitution. Check your answer. y = 3 x 2 - 3 x + 1 y = -3 x + 4 Holt Mc. Dougal Algebra 1

Nonlinear Systems Check It Out! Example 2 Continued The solutions are ( – 1, 7) and (1, 1). Holt Mc. Dougal Algebra 1

Nonlinear Systems Remember! The elimination method is a good choice when both equations have the same variable term with the same or opposite coefficients or when a variable term in one equation is a multiple of the corresponding variable term in the other equation. Holt Mc. Dougal Algebra 1

Nonlinear Systems Example 3 : Solving a Nonlinear System by Elimination. Solve each system by elimination. A 3 x - y = 1 y = x 2 + 4 x - 7 Holt Mc. Dougal Algebra 1

Nonlinear Systems Example 3 : Continued The solution is (– 3, – 10 ) and (2, 5). Holt Mc. Dougal Algebra 1

Nonlinear Systems Example 3 : Continued B y = 2 x 2 + x - 1 x - 2 y = 6 Holt Mc. Dougal Algebra 1

Nonlinear Systems Example 3 : Continued - 1 ± √– 63 x= 8 Holt Mc. Dougal Algebra 1 Since the discriminant is negative, there are no real solutions

Nonlinear Systems Check It Out! Example 3 1. Solve each system by elimination. Check your answers. . a 2 x - y = 2 y = x 2 - 5 Holt Mc. Dougal Algebra 1

Nonlinear Systems Check It Out! Example 3 Continued The solution is (3, 4) and (– 1, – 4). Holt Mc. Dougal Algebra 1

Nonlinear Systems Remember! The elimination method is a good choice when both equations have the same variable term with the same or opposite coefficients or when a variable term in one equation is a multiple of the corresponding variable term in the other equation. Holt Mc. Dougal Algebra 1

Nonlinear Systems Lesson Quiz: Part-1 Solve each system by the indicated method. 1. Graphing: 2. Substitution: Holt Mc. Dougal Algebra 1 y = x 2 - 4 x + 3 y=x-1 y = 2 x 2 - 9 x - 5 y = -3 x + 3 (1, 0), (4, 3) (-1, 6), (4, -9)

Nonlinear Systems Lesson Quiz: Part-2 3. Elimination: y = x 2 + 2 x - 3 x-y=5 no solution 4. Elimination: y = x 2 - 7 x + 10 2 x - y = 8 (3, -2), (6, 4) Holt Mc. Dougal Algebra 1