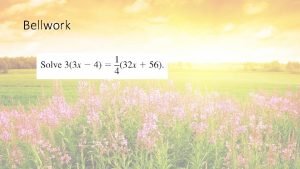4 1 QUADRATIC FUNCTIONS AND TRANSFORMATIONS Learning Goal

4. 1 QUADRATIC FUNCTIONS AND TRANSFORMATIONS Learning Goal identify and graph quadratic functions

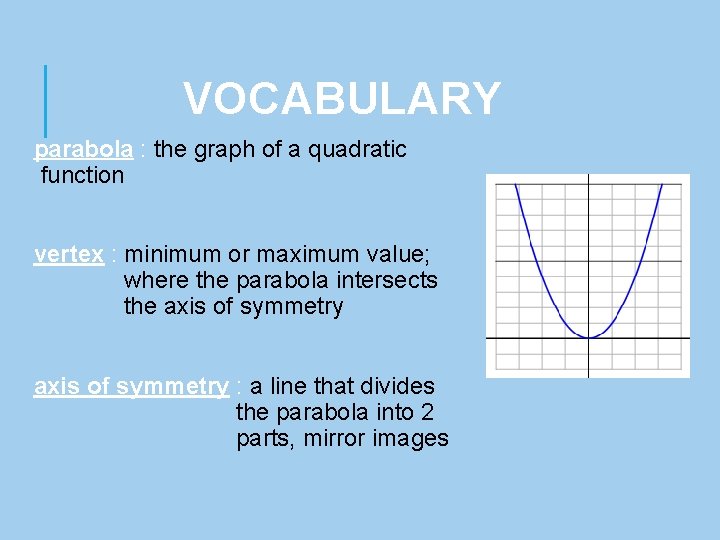
VOCABULARY parabola : the graph of a quadratic function vertex : minimum or maximum value; where the parabola intersects the axis of symmetry : a line that divides the parabola into 2 parts, mirror images

FINDING THE VERTEX OF A PARABOLA equation vertex form vertex

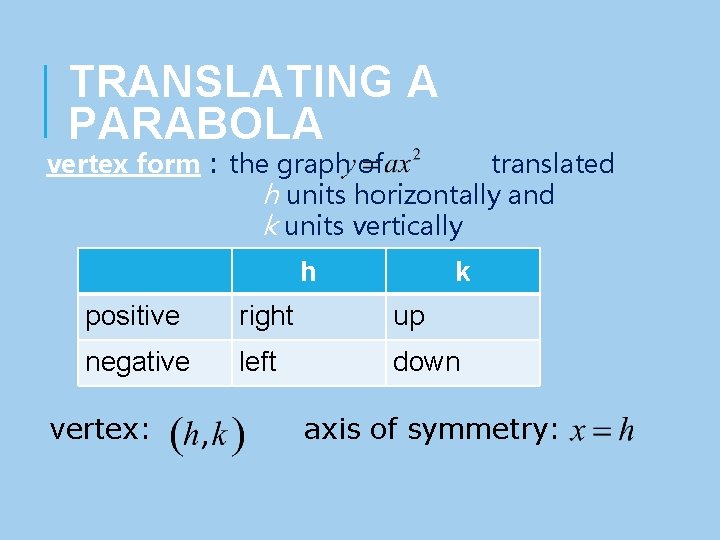
TRANSLATING A PARABOLA vertex form : the graph of translated h units horizontally and k units vertically h k positive right up negative left down vertex: axis of symmetry:

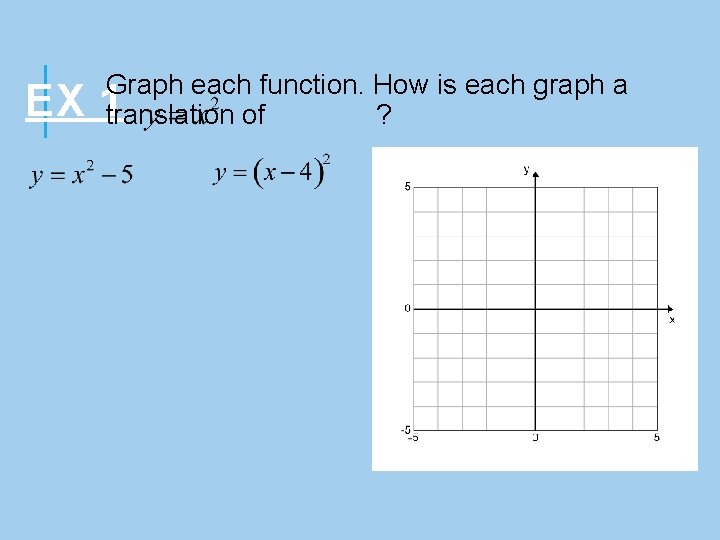
EX Graph each function. How is each graph a 1 translation of ?

REFLECTING A PARABOLA vertex form : the graph of axis value of a direction of opening min/max value positive up minimum negative down maximum reflected in the x- range graph

EX 2 Determine the direction of opening for each quadratic function. Determine if the function has a minimum or maximum and state its value.

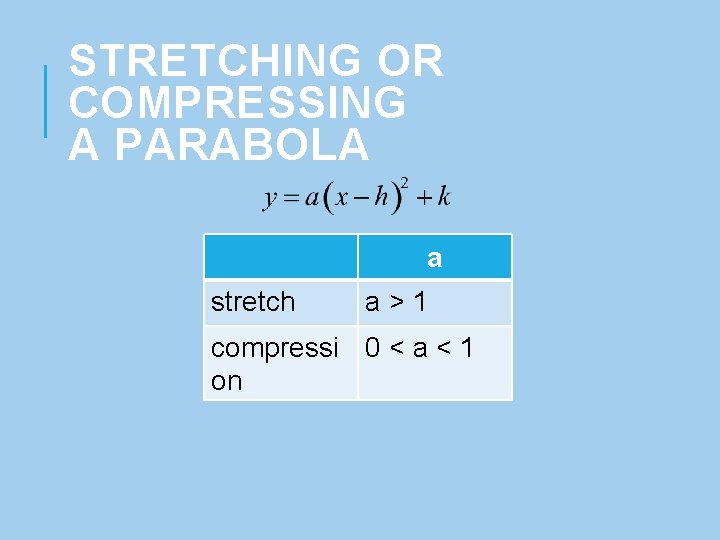
STRETCHING OR COMPRESSING A PARABOLA a stretch a>1 compressi 0 < a < 1 on

EX 3 Determine if each quadratic function is stretched or compressed.

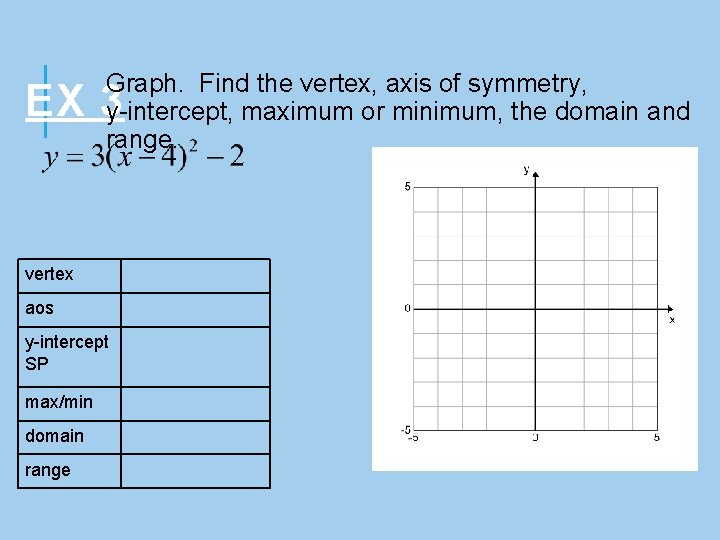
Graph. Find the vertex, axis of symmetry, y-intercept, maximum or minimum, the domain and range. EX 3 vertex aos y-intercept SP max/min domain range

Graph. Find the vertex, axis of symmetry, y-intercept, maximum or minimum, the domain and range. EX 4 vertex aos y-intercept SP max/min domain range

WRITING THE EQUATION OF A PARABOLA an equation of the quadratic EX 4 Write function in vertex form with

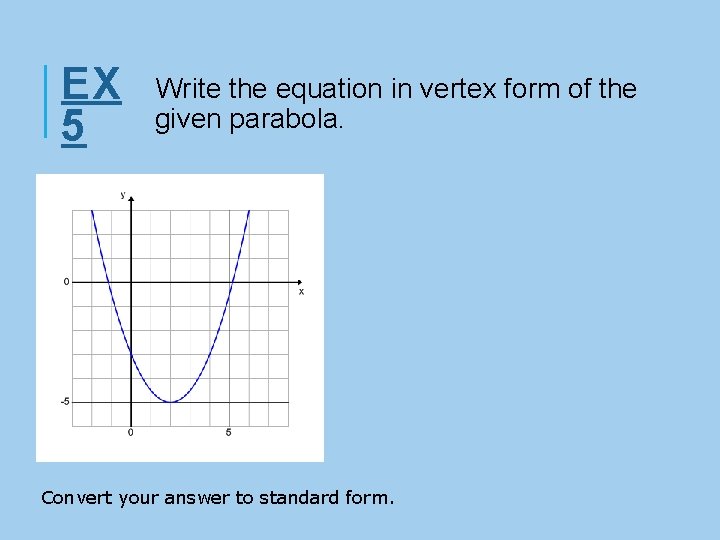
EX 5 Write the equation in vertex form of the given parabola. Convert your answer to standard form.

EX 6 Write a quadratic function in vertex form that models the path of the dolphin’s jump.