Midsegments of Triangles GEOMETRY LESSON 5 1 For

Midsegments of Triangles GEOMETRY LESSON 5 -1 (For help, go to Lesson 1 -6 and page 151. ) Find the coordinates of the midpoint of each segment. 1. AB with A(– 2, 3) and B(4, 1) 2. CD with C(0, 5) and D(3, 6) 3. EF with E(– 4, 6) and F(3, 10) 4. GH with G(7, 10) and H(– 5, – 8) Find the slope of the line containing each pair of points. 5. A(– 2, 3) and B(3, 1) 6. C(0, 5) and D(3, 6) 7. E(– 4, 6) and F(3, 10) 8. G(7, 10) and H(– 5, – 8) 5 -1

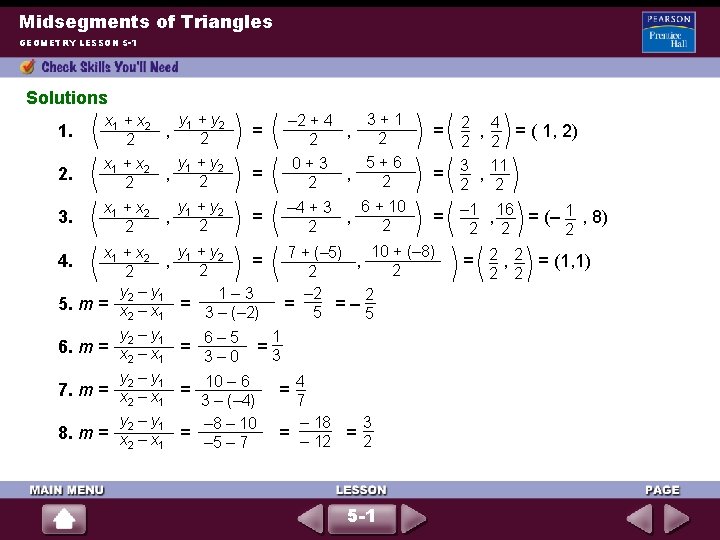
Midsegments of Triangles GEOMETRY LESSON 5 -1 Solutions 1. 2. 3. 4. 5. m 6. m 7. m 8. m y 1 + y 2 x 1 + x 2 , 2 2 y 1 + y 2 x 1 + x 2 , 2 y –y = x 2 – x 1 2 1 y 2 – y 1 = x –x 2 1 3+1 – 2 + 4 , 2 2 5+6 0+3 , 2 2 6 + 10 – 4 + 3 , 2 2 = = = y 1 + y 2 = 2 1– 3 = 3 – (– 2) = 6– 5 3– 0 10 – 6 3 – (– 4) – 8 – 10 = – 5 – 7 = = – 1 , 16 = (– 1 , 8) 10 + (– 8) 7 + (– 5) , 2 2 – 2 2 = 5 =– 5 1 =3 4 7 – 18 3 = – 12 = 5 -1 2 4 , = ( 1, 2) 2 2 3 11 , 2 2 2 = 2 , 2 = (1, 1) 2 2

Midsegments of Triangles GEOMETRY LESSON 5 -1 In XYZ, M, N, and P are midpoints. The perimeter of MNP is 60. Find NP and YZ. Because the perimeter of MNP is 60, you can find NP. NP + MN + MP = 60 Definition of perimeter NP + 24 + 22 = 60 Substitute 24 for MN and 22 for MP. NP + 46 = 60 Simplify. NP = 14 Subtract 46 from each side. Use the Triangle Midsegment Theorem to find YZ. 1 MP = 2 YZ 1 Triangle Midsegment Theorem 22 = 2 YZ Substitute 22 for MP. 44 = YZ Multiply each side by 2. 5 -1

Midsegments of Triangles GEOMETRY LESSON 5 -1 Find m AMN and m ANM. MN and BC are cut by transversal AB , so B are corresponding angles. AMN and MN || BC by the Triangle Midsegment Theorem, so AMN B because parallel lines cut by a transversal form congruent corresponding angles. m AMN = 75 because congruent angles have the same measure. In AMN, AM = AN, so m Triangle Theorem. m ANM = 75 by substituting 75 for m 5 -1 AMN by the Isosceles AMN.

Midsegments of Triangles GEOMETRY LESSON 5 -1 Explain why Dean could use the Triangle Midsegment Theorem to measure the length of the lake. Solution: To find the length of the lake, Dean starts at the end of the lake and paces straight along that end of the lake. He counts the number of strides (35). Where the lake ends, he sets a stake. He paces the same number of strides (35) in the same direction and sets another stake. The first stake marks the midpoint of one side of a triangle. Dean paces from the second stake straight to the other end of the lake. He counts the number of his strides (236). 5 -1

Midsegments of Triangles GEOMETRY LESSON 5 -1 (continued) Dean finds the midsegment of the second side by pacing exactly half the number of strides back toward the second stake. He paces 118 strides. From this midpoint of the second side of the triangle, he returns to the midpoint of the first side, counting the number of strides (128). Dean has paced a triangle. He has also formed a midsegment of a triangle whose third side is the length of the lake. By the Triangle Midsegment Theorem, the segment connecting the two midpoints is half the distance across the lake. So, Dean multiplies the length of the midsegment by 2 to find the length of the lake. 5 -1

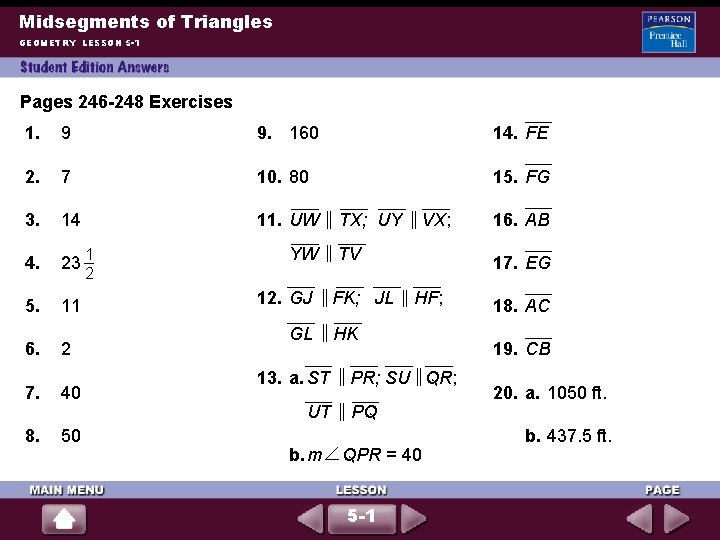
Midsegments of Triangles GEOMETRY LESSON 5 -1 Pages 246 -248 Exercises 1. 9 9. 160 14. FE 2. 7 10. 80 15. FG 3. 14 11. UW 4. 23 5. 11 6. 2 7. 40 8. 50 1 2 YW 12. GJ GL 13. a. ST UT b. m TX; UY VX; TV FK; JL 17. EG HF; HK PR; SU QR; PQ QPR = 40 5 -1 16. AB 18. AC 19. CB 20. a. 1050 ft. b. 437. 5 ft.

Midsegments of Triangles GEOMETRY LESSON 5 -1 21. a. 114 ft. 9 in. 26. (continued) b. Slope of HJ = 2 = 1; b. Answers may vary. Sample: The highlighted segment is the midsegment of the triangular face of the building. 2 Slope of EF = 4 = 1; 4 therefore HJ c. HJ = EF = 22. 60 EF. 22 + 2 2 = 42 + 4 2 = 8=2 2; 32 = 4 2 ; therefore HJ = 1 EF. 23. 45 2 24. 100 27. 18 1 25. 55 28. 37 26. a. H(2, 0); J(4, 2) 29. 60 2 5 -1

Midsegments of Triangles GEOMETRY LESSON 5 -1 30. 50 31. 10 37. (continued) so that CA = AP. Find B, the midpt. Of PD. Then, by the Midsegment Thm. , AB CD and AB = 1 2 CD. 32. x = 6; y = 6 1 2 33. 154 cm 38. G(4, 4); H(0, 2); J(8, 0) 34. 52 39. 35. x = 3; DF = 24 36. x = 9; EC = 26 37. Answers may vary. Sample: Draw CA and extend CA to P UTS; Proofs may vary; Sample: VS SY, YT TZ, and VU UZ because S, T, and U are 1 midpts. of the respective sides; ST = 2 VZ so 1 ST VU UZ; SU = 2 YZ so SU YT TZ; and TU = 1 VY so TU 2 YST TUZ 5 -1 SY SVU SV; therefore UTS by SSS.

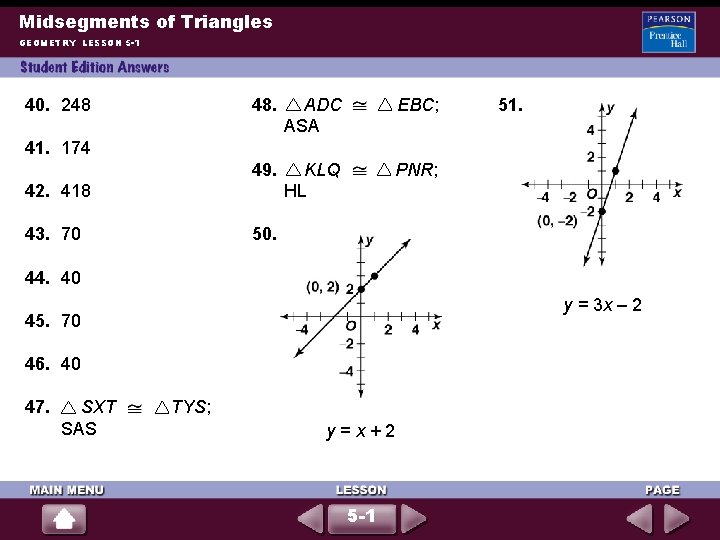
Midsegments of Triangles GEOMETRY LESSON 5 -1 40. 248 48. ADC ASA EBC; 49. KLQ HL PNR; 51. 41. 174 42. 418 43. 70 50. 44. 40 y = 3 x – 2 45. 70 46. 40 47. SXT SAS TYS; y=x+2 5 -1

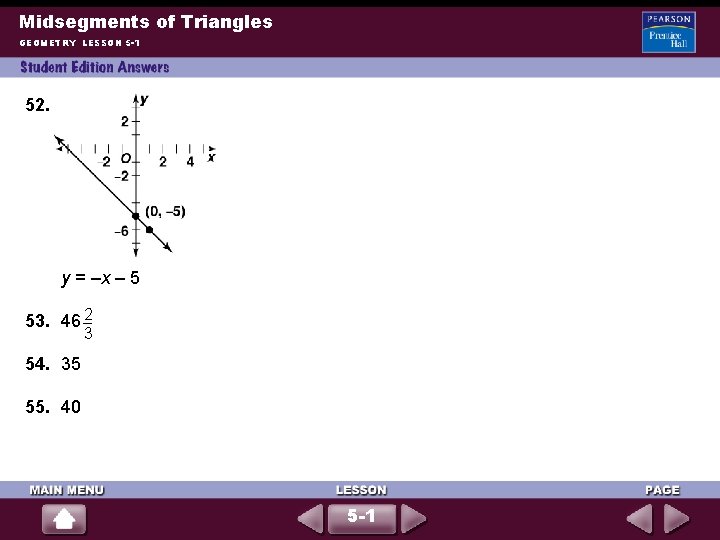
Midsegments of Triangles GEOMETRY LESSON 5 -1 52. y = –x – 5 53. 46 2 3 54. 35 55. 40 5 -1

Midsegments of Triangles GEOMETRY LESSON 5 -1 In GHI, R, S, and T are midpoints. 1. Name all the pairs of parallel segments. RT || HI, RS || GI, ST || HG 2. If GH = 20 and HI = 18, find RT. 9 3. If RH = 7 and RS = 5, find ST. 7 4. If m G = 60 and m I = 70, find m GTR. 70 5. If m H = 50 and m I = 66, find m ITS. 64 6. If m G = m H = m I and RT = 15, find the perimeter of 90 5 -1 GHI.

Bisectors in Triangles GEOMETRY LESSON 5 -2 (For help, go to Lesson 1 -5. ) Use a compass and a straightedge for the following. 1. Draw a triangle, 2. Draw acute XYZ. Construct P. Construct STV so that Q so that 3. Draw AB. Construct a line CD so that CD 4. Draw acute angle TM bisects STU so that m P. E. STM = 5 x + 4 and m STU. 5 -2 XYZ. AB and CD bisects AB. E. Construct the bisector of 5. Find the value of x. 6. Find m Q STV MTU = 6 x – 2.

Bisectors in Triangles GEOMETRY LESSON 5 -2 Solutions 1 -4. Answers may vary. Samples given: 1. 2. 3. 4. 5. Since TM bisects STU, m STM = m MTU. So, 5 x + 4 = 6 x – 2. Subtract 5 x from both sides: 4 = x – 2; add 2 to both sides: x = 6. 6. From Exercise 5, x = 6. m STU = m = 11 x + 2 = 11(6) + 2 = 68. 5 -2 STM + m MTU = 5 x + 4 + 6 x – 2

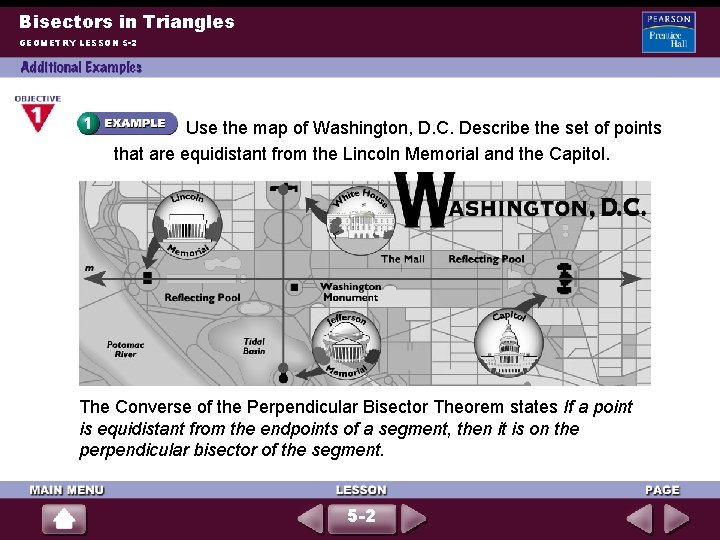
Bisectors in Triangles GEOMETRY LESSON 5 -2 Use the map of Washington, D. C. Describe the set of points that are equidistant from the Lincoln Memorial and the Capitol. The Converse of the Perpendicular Bisector Theorem states If a point is equidistant from the endpoints of a segment, then it is on the perpendicular bisector of the segment. 5 -2

Bisectors in Triangles GEOMETRY LESSON 5 -2 (continued) A point that is equidistant from the Lincoln Memorial and the Capitol must be on the perpendicular bisector of the segment whose endpoints are the Lincoln Memorial and the Capitol. Therefore, all points on the perpendicular bisector of the segment whose endpoints are the Lincoln Memorial and the Capitol are equidistant from the Lincoln Memorial and the Capitol. 5 -2

Bisectors in Triangles GEOMETRY LESSON 5 -2 Find x, FB, and FD in the diagram above. FD = FB Angle Bisector Theorem 7 x – 37 = 2 x + 5 Substitute. 7 x = 2 x + 42 Add 37 to each side. 5 x = 42 Subtract 2 x from each side. x = 8. 4 Divide each side by 5. FB = 2(8. 4) + 5 = 21. 8 Substitute. FD = 7(8. 4) – 37 = 21. 8 Substitute. 5 -2

Bisectors in Triangles GEOMETRY LESSON 5 -2 Pages 251 -254 Exercises 1. AC is the BD bis. of 7. y = 3; ST = 15; TU = 15 12. 5 13. 10 2. 3. 15 18 8. HL is the bis. of JHG because a point on HL is equidistant from J and G. 4. 8 5. The set of points equidistant from H and S is the bis. of HS. 9. y = 9; m FHL = 54; m KHL = 54 x = 12; JK = 17; JM =17 11. Point E is on the bisector of KHF. 6. 10. 27 5 -2 14. 10 15. Isosceles; it has 2 sides 16. equidistant; RT = RZ 17. A point on the bis. of a segment if and only if it is equidistant from the endpoints of the segment.

Bisectors in Triangles GEOMETRY LESSON 5 -2 18. 12 19. 4 20. 4 21. 16 26. (continued) and CT = CY by the Bis. Thm. 31. The pitcher’s plate 32. a. 27. Answers may vary. Sample: the student needs to know that QS bisects PR. 22. 5 23. 10 28. No; A is not equidistant from the sides of X. 24. 7 29. Yes; AX bis. TXR. 25. 14 26. Isosceles: CS = CT 30. Yes; A is equidistant from the sides of X. 5 -2 b. The bisectors intersect at the same point. c. Check student's work.

Bisectors in Triangles GEOMETRY LESSON 5 -2 33. a. 34 -39. Answers may vary. Samples are given. 34. C(0, 2), D(1, 2); AC = BC = 2, AD = BD = 5 35. C(3, 2), D(3, 0); AC = BC = 3, AD = BD = 13 36. C(3, 0), D(3, 0); AC = BC = 3, AD = BD = 3 b. The bisectors intersect at the same point. 37. C(0, 0), D(1, 1); AC = BC = 3, AD = BD = c. Check students’ work 38. C(2, 2), D(4, 3); AC = BC = 5, AD = BD = 5 -2 2 5 10

Bisectors in Triangles GEOMETRY LESSON 5 -2 5 5 39. C 2 , D(5, 3); 26 AC = BC = , AD = BD = 2 40. a. 43. (continued) 13 : y = – 3 x + 25 ; x = 10 4 5 b. (10, 5) c. CA = CB = 5 d. C is equidist. from OA and OB. 41. bisector; right; Reflexive; SAS; CPCTC 42. PQ; BAQ; CPCTC; bisector 43. Answers may vary. Sample: proof of the Conv. of the Bis. Thm. 5 -2

Bisectors in Triangles GEOMETRY LESSON 5 -2 44. x = 3 45. y = –(x – 2) 46. y = – 1 x + 4 47. (continued) by A, B, and C and if it goes through the point that is the intersection of the bisectors of the sides of ABC. 2 47. 48. BP AB and PC AC, thus ABP and ACP are rt. s. Since AP bisects BAC, BAP CAP. AP AP by the Reflexive Prop. of. Thus ABP ACP by AAS and PB PC by CPCTC. Therefore, PB = PC. Line is equidistant from points A, B, and C if it is to the plane determined 5 -2

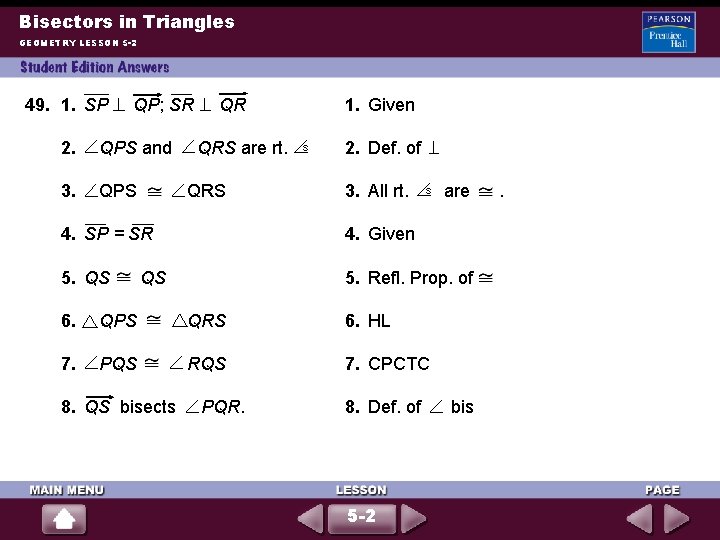
Bisectors in Triangles GEOMETRY LESSON 5 -2 49. 1. SP QP; SR 2. QPS and 3. QPS QR QRS are rt. QRS 1. Given s 2. Def. of 3. All rt. s are 4. SP = SR 4. Given 5. QS 5. Refl. Prop. of QS 6. QPS QRS 6. HL 7. PQS RQS 7. CPCTC 8. QS bisects PQR. 8. Def. of 5 -2 bis .

Bisectors in Triangles GEOMETRY LESSON 5 -2 50. D 51. H 52. D 53. [2] Since MK MR, MK KV, and MR RV, the Bisector Thm. states that MV is the bisector of KVR. 54. [4] (continued) MRV are rt. . s. By HL, MKV MRV. By CPCTC, KV RV. By the Converse of the Bisector Thm. , points M and V lie on the bisector, so MV is the bisector of KR [3]appropriate steps with one logical error OR one incorrect reason statement [1] partially correct logical argument [2]two logical errors OR two incorrect reasons statements 54. [4] MK MR. By the Reflexive Prop. of , MV MV. It is given that MKV and sbut failed to reach [1]proved desired conclusion 5 -2

Bisectors in Triangles GEOMETRY LESSON 5 -2 55. 8 63. Trans. Prop. of 56. 4 64. C 3, 57. 6 65. C 0, 7 ; AB = 97, AC = BC = 58. Reflexive Prop. of = 66. C 11 , 5 ; AB = 17, AC = CB = 17 13 ; AB = 3 2 2 2 59. Div. Prop. of = 60. Add. Prop. of = 61. Distr. Prop. 62. Subst. or Transitive Prop. of = 5 -2 5, AC = CB = 3 5 2 97 2 2

Bisectors in Triangles GEOMETRY LESSON 5 -2 Use this figure for Exercises 1– 3. Use this figure for Exercises 4– 6. 1. Find BD. 4. Find the value of x. 16 6 2. Complete the statement: 5. Find CG. C is equidistant from ? . 8 points A and B 3. Can you conclude that 6. Find the perimeter of CN = DN? Explain. quadrilateral ABCG. No; if AB were the perpendicular 48 bisector of CD, then AND BNC, but BC =/ AD. 5 -2

Concurrent Lines, Medians, and Altitudes GEOMETRY LESSON 5 -3 (For help, go to Lesson 1 -5. ) Draw a large triangle. Construct each figure. 1. an angle bisector 2. a perpendicular bisector of a side 3. Draw GH Construct CD GH at the midpoint of GH. 4. Draw AB with a point E not on AB. Construct EF 5 -3 AB.

Concurrent Lines, Medians, and Altitudes GEOMETRY LESSON 5 -3 Solutions Answers may vary. Samples given: 1– 2. 3. 4. 5 -3

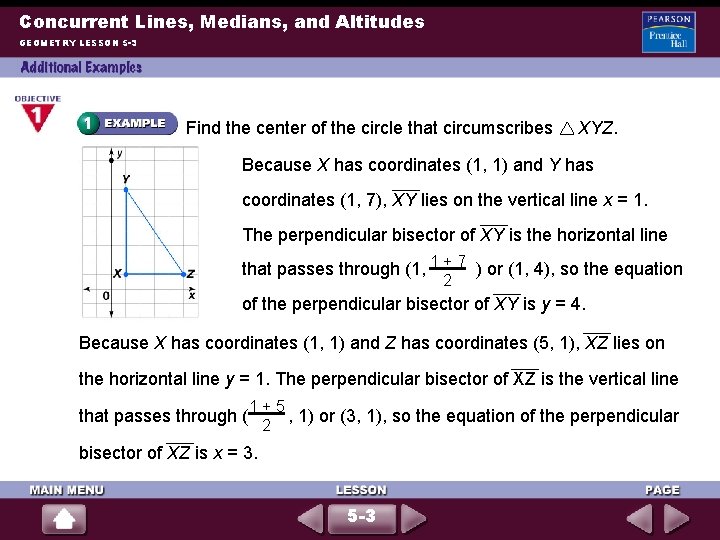
Concurrent Lines, Medians, and Altitudes GEOMETRY LESSON 5 -3 Find the center of the circle that circumscribes XYZ. Because X has coordinates (1, 1) and Y has coordinates (1, 7), XY lies on the vertical line x = 1. The perpendicular bisector of XY is the horizontal line that passes through (1, 1 + 7 ) or (1, 4), so the equation 2 of the perpendicular bisector of XY is y = 4. Because X has coordinates (1, 1) and Z has coordinates (5, 1), XZ lies on the horizontal line y = 1. The perpendicular bisector of XZ is the vertical line 1+5 that passes through ( 2 , 1) or (3, 1), so the equation of the perpendicular bisector of XZ is x = 3. 5 -3

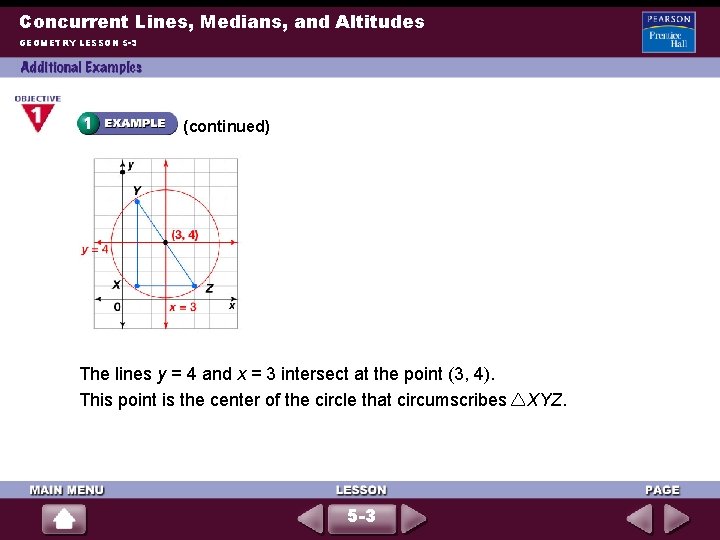
Concurrent Lines, Medians, and Altitudes GEOMETRY LESSON 5 -3 (continued) The lines y = 4 and x = 3 intersect at the point (3, 4). This point is the center of the circle that circumscribes 5 -3 XYZ.

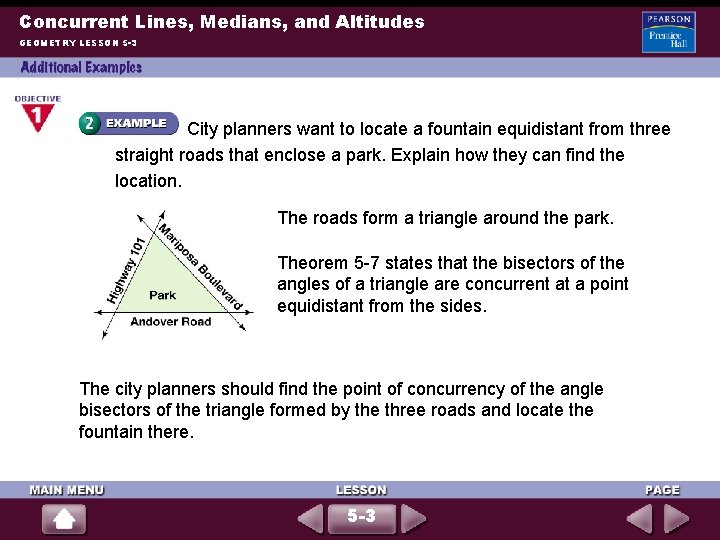
Concurrent Lines, Medians, and Altitudes GEOMETRY LESSON 5 -3 City planners want to locate a fountain equidistant from three straight roads that enclose a park. Explain how they can find the location. The roads form a triangle around the park. Theorem 5 -7 states that the bisectors of the angles of a triangle are concurrent at a point equidistant from the sides. The city planners should find the point of concurrency of the angle bisectors of the triangle formed by the three roads and locate the fountain there. 5 -3

Concurrent Lines, Medians, and Altitudes GEOMETRY LESSON 5 -3 M is the centroid of WOR, and WM = 16. Find WX. The centroid is the point of concurrency of the medians of a triangle. The medians of a triangle are concurrent at a point that is two thirds the distance from each vertex to the midpoint of the opposite side. (Theorem 5 -8) Because M is the centroid of 2 WM = 3 WX 16 = 2 WX 3 24 = WX 2 WOR, WM = 3 WX. Theorem 5 -8 Substitute 16 for WM. 3 Multiply each side by 2. 5 -3

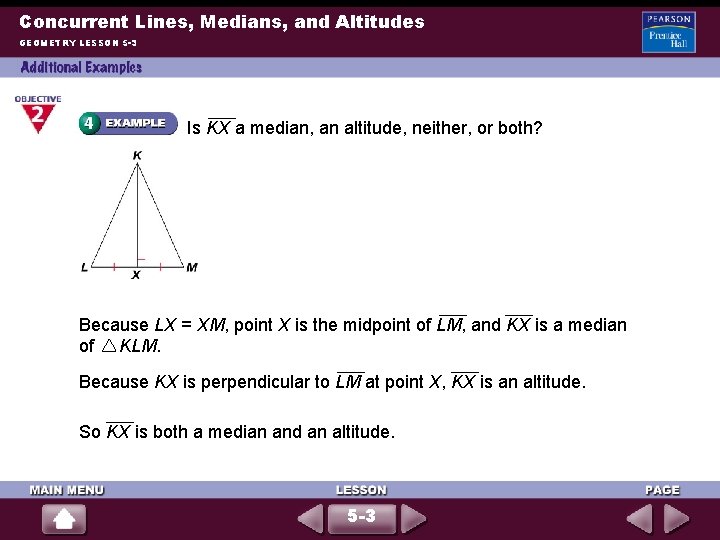
Concurrent Lines, Medians, and Altitudes GEOMETRY LESSON 5 -3 Is KX a median, an altitude, neither, or both? Because LX = XM, point X is the midpoint of LM, and KX is a median of KLM. Because KX is perpendicular to LM at point X, KX is an altitude. So KX is both a median and an altitude. 5 -3

Concurrent Lines, Medians, and Altitudes GEOMETRY LESSON 5 -3 Pages 259 -263 Exercises 1. (– 2, – 3) 8. C 12. ZY = 4 1 ; ZU = 13 1 2. (0, 0) 9. Z 13. VY = 6; YX = 3 3. 11 , 1 14. Median; A is a midpt. 4. 2, – 1 1 5. – 3, 1 1 6. – 3, – 4 1 10. Find the bisectors of the sides of the formed by the tennis court, the playground, and the volleyball court. That point will be equidistant from the vertices of the. 7. 31, 3 11. TY = 18; TW = 27 2 2 2 5 -3 2 15. Neither; it’s not a segment drawn from a vertex. 16. Altitude; AB is a segment drawn from a vertex of a perp. to the opp. side.

Concurrent Lines, Medians, and Altitudes GEOMETRY LESSON 5 -3 17. 18. 5 -3 …

Concurrent Lines, Medians, and Altitudes GEOMETRY LESSON 5 -3 19. BE 27. bisector; it bisects an. 20. FC 21. CA 22. DG 28. None of these; it is a midsegment 29. Altitude; AB is to a side from a vertex. 23. 1: 2 or 2: 1 25 -26. Check student’s work. b. Bis. Thm. c. Trans. d. Bis. b. AM: y = 3 x; b. BC 5 BN: y = – 3 x + 12; c. XC d. Bis. Thm. 32. a. L(1, 3); M(5, 3); N(4, 0) 30. a. AB 24. Find the circumcenter of the formed by the three pines. 31. a. bis. 5 -3 CL: y = – 3 + 24 7 7

Concurrent Lines, Medians, and Altitudes GEOMETRY LESSON 5 -3 32. (continued) c. 10 , 2 3 d. – 3 10 + 24 = – 10 + 24 = 14 = 2 7 3 7 7 136 = 2 9 3 34; BN = 40 = 2 BP = 160 = 4 10; CL = 3 9 232 = 58 3 9 58; e. AM = CP = 34; AP = 10; 35. Answers may vary. Sample: Let ABC be isosc. with base s B and C. If AD bisects A, then it is to BC, and therefore the altitude from A. So, AD contains the circumcenter, incenter, centroid, and orthocenter. 33. I-D; II-B; III-C; IV-A 36. 34. I-A; II-C; III-B; IV-D 37. C 5 -3 bisectors

Concurrent Lines, Medians, and Altitudes GEOMETRY LESSON 5 -3 38. H 39. D 40. [2]any acute ; or a list that contains all of the following: equiangular s , equilateral s , acute isosceles , s acute scalene s 40. [1] (continued) equilateral s , acute isosceles scalene s 41. [4] 41. [1] a list that does not contain equiangular s , 5 -3 s , or acute

Concurrent Lines, Medians, and Altitudes GEOMETRY LESSON 5 -3 41. [4] (continued) 43. No; point B is equidistant from the sides. 44. No; point B is not necessarily equidistant from the sides. 45. right [3] one diagram partially or completely incorrect 46. obtuse [2] two diagrams partially or completely incorrect [1]three diagrams partially or completely incorrect 42. Yes; TB bisects the . 5 -3

Concurrent Lines, Medians, and Altitudes GEOMETRY LESSON 5 -3 47 -51. Answers may vary. Samples are given. 47. AB 48. AD 49. ABC and ADE 50. AB and CD 51. BC 5 -3

Concurrent Lines, Medians, and Altitudes GEOMETRY LESSON 5 -3 1. Complete the sentence: To find the centroid of a triangle, you need to draw at least ? median(s). two 2. FGH has vertices F(– 1, 2), G(9, 2), and H(9, 0). Find the center of the circle that circumscribes FGH. (4, 1) Use the diagram for Exercises 3– 5. 3. Identify all medians and altitudes drawn in PSV. PX and SY are medians; VZ is an altitude. 4. If SY = 15, find SM and MY. SM = 10 and MY = 5 5. If MX = 14, find PM and PX. PM = 28 and PX = 42 5 -3

Inverses, Contrapositives, and Indirect Reasoning GEOMETRY LESSON 5 -4 (For help, go to Lesson 2 -1 and 2 -2. ) Write the converse of each statement. 1. If it snows tomorrow, then we will go skiing. 2. If two lines are parallel, then they do not intersect. 3. If x = – 1, then x 2 = 1. Write two conditional statements that make up each biconditional. 4. A point is on the bisector of an angle if and only if it is equidistant from the sides of the angle. 5. A point is on the perpendicular bisector of a segment if and only if it is equidistant from the endpoints of the segment. 6. You will pass a geometry course if and only if you are successful with your homework. 5 -4

Inverses, Contrapositives, and Indirect Reasoning GEOMETRY LESSON 5 -4 Solutions 1. Switch the hypothesis and conclusion: If we go skiing tomorrow, then it snows. 2. Switch the hypothesis and conclusion: If two lines do not intersect, then they are parallel. 3. If x 2 = 1, then x = – 1. 4. Rewrite the statement as an if-then statement; then rewrite it by writing its converse: If a point is on the bisector of an angle, then it is equidistant from the sides of the angle. If a point is equidistant from the sides of an angle, then it is on the bisector of the angle. 5. Rewrite the statement as an if-then statement; then rewrite it by writing its converse: If a point is on the perpendicular bisector of a segment, then it is equidistant from the endpoints of the segment. If a point is equidistant from the endpoints of a segment, then it is on the perpendicular bisector of the segment. 6. Rewrite the statement as an if-then statement; then rewrite it by writing its converse: If you pass a geometry course, then you are successful with your geometry homework. If you are successful with your geometry homework, then you will pass the geometry course. 5 -4

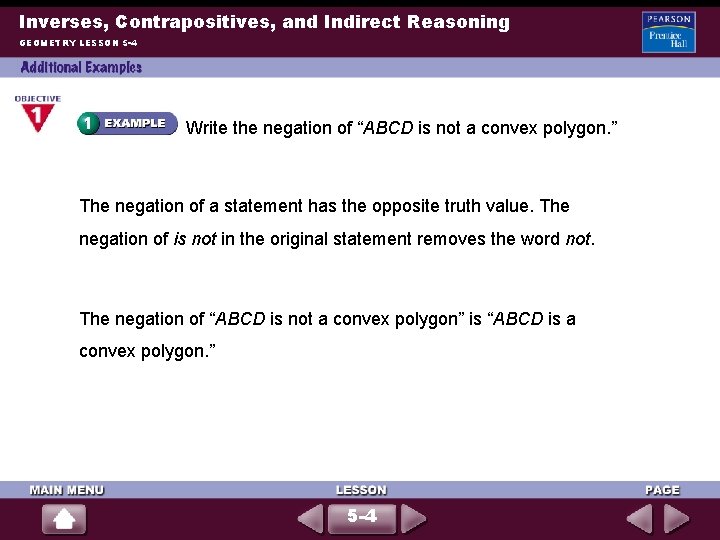
Inverses, Contrapositives, and Indirect Reasoning GEOMETRY LESSON 5 -4 Write the negation of “ABCD is not a convex polygon. ” The negation of a statement has the opposite truth value. The negation of is not in the original statement removes the word not. The negation of “ABCD is not a convex polygon” is “ABCD is a convex polygon. ” 5 -4

Inverses, Contrapositives, and Indirect Reasoning GEOMETRY LESSON 5 -4 Write the inverse and contrapositive of the conditional statement “If ABC is equilateral, then it is isosceles. ” To write the inverse of a conditional, negate both the hypothesis and the conclusion. Hypothesis Conclusion Conditional: If Inverse: If ABC is equilateral, then it is isosceles. Negate both. ABC is not equilateral, then it is not isosceles. To write the contrapositive of a conditional, switch the hypothesis and conclusion, then negate both. Conditional: If ABC is isosceles, then it is equilateral. Switch and negate both. Contrapositive: If ABC is not equilateral, 5 -4 then it is not isosceles.

Inverses, Contrapositives, and Indirect Reasoning GEOMETRY LESSON 5 -4 Write the first step of an indirect proof. Prove: A triangle cannot contain two right angles. In the first step of an indirect proof, you assume as true the negation of what you want to prove. Because you want to prove that a triangle cannot contain two right angles, you assume that a triangle can contain two right angles. The first step is “Assume that a triangle contains two right angles. ” 5 -4

Inverses, Contrapositives, and Indirect Reasoning GEOMETRY LESSON 5 -4 Identify the two statements that contradict each other. I. P, Q, and R are coplanar. Two statements contradict each other II. P, Q, and R are collinear. when they cannot both be true III. m PQR = 60 at the same time. Examine each pair of statements to see whether they contradict each other. II and III P, Q, and R are collinear, and coplanar, and m PQR = 60. collinear. m PQR==60. Three points that lie on the same line are both coplanar and collinear, so these two statements do not contradict each other. Three points that lie on an angle are coplanar, so these two statements do not contradict each other. 5 -4 If three distinct points are collinear, they form a straight angle, so m PQR cannot equal 60. Statements II and III contradict each other.

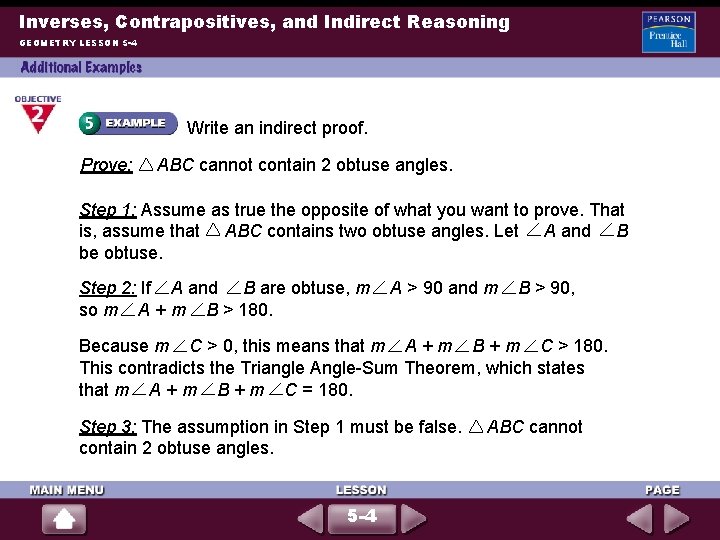
Inverses, Contrapositives, and Indirect Reasoning GEOMETRY LESSON 5 -4 Write an indirect proof. Prove: ABC cannot contain 2 obtuse angles. Step 1: Assume as true the opposite of what you want to prove. That is, assume that ABC contains two obtuse angles. Let A and B be obtuse. Step 2: If A and B are obtuse, m so m A + m B > 180. A > 90 and m B > 90, Because m C > 0, this means that m A + m B + m C > 180. This contradicts the Triangle Angle-Sum Theorem, which states that m A + m B + m C = 180. Step 3: The assumption in Step 1 must be false. contain 2 obtuse angles. 5 -4 ABC cannot

Inverses, Contrapositives, and Indirect Reasoning GEOMETRY LESSON 5 -4 Pages 267 -270 Exercises 1. Two angles are not congruent 2. You are sixteen years old 3. 4. 5. 6. The angle is obtuse The soccer game is not on Friday The figure is not a triangle m A ≥ 90 7. a. If you don’t eat all of your vegetables, then you won’t grow. b. If you won’t grow, then you don’t eat all of your vegetables. 8. a. If a figure is not a square, then at least one of its angles is not a right angle. 5 -4 8. (continued) b. If at least one of the angles is not a right angle, then the figure is not a square. 9. a. If a figure isn’t a rectangle, then it doesn’t have four sides b. If a figure doesn’t have four sides, then it isn’t a rectangle

Inverses, Contrapositives, and Indirect Reasoning GEOMETRY LESSON 5 -4 10. Assume that it is not raining outside. 15. Assume that m 2 ≤ 90. 11. Assume that a right angle. 16. I and II 20. (continued) c. the Debate Club has fewer than 10 members 17. I and II 21. a. right angle J is 12. Assume that PEN is not isosceles. 13. Assume that none of the angles is obtuse. 14. Assume that XY AB 18. I and III b. right angles 19. II and III c. 90 20. a. 20 or more d. 180 b. the Debate Club and the Chess Club have fewer than 20 members 5 -4 e. 90 f. 90

Inverses, Contrapositives, and Indirect Reasoning GEOMETRY LESSON 5 -4 21. (continued) g. 0 h. more than one right angle i. at most one right angle 22. a. If you don’t live in Sarasota, then you don’t live in Florida; false 23. a. If four points aren’t collinear, then they aren’t coplanar; false b. If four points aren’t coplanar, then they aren’t collinear; true 24 -27. Answers may vary. Samples are given. 24. If a figure is a square, then it has four right angles. 25. If today is Sunday, then tomorrow is Monday. 26. Not possible; a conditional and its contrapositive have the same truth value. 27. If two sides of a triangle are congruent, then the triangle is isosceles. b. If you don’t live in Florida, then you don’t live in Sarasota; true 5 -4

Inverses, Contrapositives, and Indirect Reasoning GEOMETRY LESSON 5 -4 28. Angie assume that the inverse of the statement was true, but a conditional and its inverse may not have the same truth value. 29. Assume that the driver did not apply the brakes. Then there would be no skid marks. This contradicts the fact that fresh skid marks appear. Thus the green car 29. (continued) applied the brakes is a true statement. 30. Assume that the temperature outside is more that 32ºF. then ice would not be forming on the sidewalk. This contradicts the fact that ice is forming. Thus the statement that the temperature must be 32ºF or less is true. 5 -4 31. Assume that an obtuse triangle can contain a right triangle. Then the sum of the measures of the obtuse angle and the right angle is more than 180. This contradicts the fact that the sum of the 3 angles of a triangle is 180. Thus the statement that an obtuse triangle cannot contain a right angle is true.

Inverses, Contrapositives, and Indirect Reasoning GEOMETRY LESSON 5 -4 32. Assume XY and XZ are two different lines to AX, with Y and Z on the same side of AX. If B is on AX opp. pt. A from X, then m AXY + m YXZ + m ZXB = 180. But m AXY = m ZXB = 90, so m YXZ = 0. Thus X, Y, and Z are collinear. 33. If the animal is a kitten, then it is a cat. If the animal isn’t a cat, then it’s not a kitten. 34. If the angle measures 120, then it is obtuse. If the angle isn’t obtuse, then it doesn’t measure 120. 35. If a number is a whole number, then it is an integer. If a number isn’t an integer, then it isn’t a whole number. 5 -4 36. Check students’ work. 37. a. Earl proves that it’s later than 5: 00. b. He starts with the assumption that it is before 5: 00. c. It is not noisy. 38. The culprit entered the room through a hole in the roof; the other possibilities were eliminated.

Inverses, Contrapositives, and Indirect Reasoning GEOMETRY LESSON 5 -4 39. Assume A B. Then BC AC since if the base s are , the sides opp. them are. But this contradicts the given BC > AC. Thus A B. 42. D. 43. G 44. D 40. Assume one base is a right. Then the other base is also a right since the base s of an isosceles are congruent. But a can have at most one right. So neither base is a right. 41. Assume XB AC. Then AXB and CXB are right s. Since m ABX = m CBX = 36, then A C because if two s of a are , the third s are. Then AB = BC since sides opp. s are , and ABC is an isosceles. But this contradicts the given statement that ABC is scalene. Thus, XB is not to AC. 5 -4 45. H

Inverses, Contrapositives, and Indirect Reasoning GEOMETRY LESSON 5 -4 46. [2]Assume that a can have more than one obtuse. Then the sum of the measures of the two obtuse s is greater than 180. But this contradicts the - -Sum Thm. So a can have at most one obtuse. [1]partially incorrect logical argument 47. XY is an altitude because of the right and a median because Y is the midpoint of the opp. side. XY is also a bis. and an bis. 48. XY is an altitude since it goes through a vertex and is to the opp. side. 49. XY is a median since it has endpoints at a vertex and the midpoint of the opp. side. 5 -4 50. corr s 51. same-side int. 52. alt. int. 53. corr. s s 54. 35 55. 45 = m ABC s

Inverses, Contrapositives, and Indirect Reasoning GEOMETRY LESSON 5 -4 1. Write the negation of the statement “ D is a straight angle. ” D is not a straight angle. 2. Identify two statements that contradict each other. I. x and y are perfect squares. II. x and y are odd. III. x and y are prime. I and III For Exercises 3– 6, use the following statement: If is parallel to m, then 1 and 2 are supplementary. 3. Write the converse. If 1 and 2 are supplementary, then is parallel to m. 4. Write the inverse. If is not parallel to m, then 1 and 2 are not supplementary. 5. Write the contrapositive. If 1 and 2 are not supplementary, then is not parallel to m. 6. Write the first step of an indirect proof. Assume that 1 and 2 are not supplementary. 5 -4

Inequalities in Triangles GEOMETRY LESSON 5 -5 (For help, go to Lesson 1 -6 and 5 -4. ) Graph the triangles with the given vertices. List the sides in order from shortest to longest. 1. A(5, 0), B(0, 8), C(0, 0) 2. P(2, 4), Q(– 5, 1), R(0, 0) 3. G(3, 0), H(4, 3), J(8, 0) 4. X(– 4, 3), Y(– 1, 1), Z(– 1, 4) Recall the steps for an indirect proof. 5. You want to prove m A > m B. Write the first step of an indirect proof. 6. In an indirect proof, you deduce that AB > AC is false. What conclusion can you make? 5 -5

Inequalities in Triangles GEOMETRY LESSON 5 -5 Solutions 1. 3. 2. 4. 5. In an indirect proof, the first step is to assume the opposite of what is to be proved: Assume that m A > m B. 6. Comparing AB and AC results in no more than two out of three possibilities: AB = AC, AB < AC, or AB > AC. Since AB > AC is false, and AB = AC are both false, then AB < AC is true. 5 -5

Inequalities in Triangles GEOMETRY LESSON 5 -5 Explain why m 4>m 5. 4 is an exterior angle of XYC. The Corollary to the Exterior Angle Theorem states that the measure of an exterior angle of a triangle is greater than the measure of each of its remote interior angles. The remote interior angles are 2 and 3, so m 4 > m 2. 2 and 5 are corresponding angles formed by AB and XY cut by transversal BC. Because AB || XY, you can conclude that 2 5 by the Corresponding Angles Postulate. Thus, m 2 = m 5. Substituting m 5 for m 2 in the inequality m 4 > m 5. 5 -5 4>m 2 produces the

Inequalities in Triangles GEOMETRY LESSON 5 -5 In RGY, RG = 14, GY = 12, and RY = 20. List the angles from largest to smallest. Theorem 5 -10 states If two sides of a triangle are not congruent, then the larger angle lies opposite the longer side. No two sides of RGY are congruent, so the larger angle lies opposite the longer side. Find the angle opposite each side. The longest side is 20. The opposite angle, G, is largest. The shortest side is 12. The opposite angle, R, is smallest. From largest to smallest, the angles are 5 -5 G, Y, R.

Inequalities in Triangles GEOMETRY LESSON 5 -5 In ABC, C is a right angle. Which is the longest side? Theorem 5 -11 states If two angles of a triangle are not congruent, then the longer side lies opposite the larger angle. Find the largest angle. m A + m B + m C = 180 by the Triangle Angle-Sum Theorem. m A + m B + 90 = 180 because the measure of a right angle is 90, so m A + m B = 90. m A < m C and m B < m so C is the largest angle. Because AB is opposite C by the Comparison Property of Inequality, C, the longest side in 5 -5 ABC is AB.

Inequalities in Triangles GEOMETRY LESSON 5 -5 Can a triangle have sides with the given lengths? Explain. a. 2 cm, 4 cm b. 8 in. , 15 in. , 12 in. According to the Triangle Inequality Theorem, the sum of the lengths of any two sides of a triangle is greater than the length of the third side. a. 2 + 2 > 4 No. The sum of 2 and 2 is not greater than 4, contradicting Theorem 5 -12. b. 8 + 15 > 12 8 + 12 > 15 15 + 12 > 8 Yes. The sum of any two lengths is greater than the third length. 5 -5

Inequalities in Triangles GEOMETRY LESSON 5 -5 In FGH, FG = 9 m and GH = 17 m. Describe the possible lengths of FH. The Triangle Inequality Theorem states the sum of the lengths of any two sides of a triangle is greater than the length of the third side. Solve three inequalities. FH + 9 > 17 FH + 17 > 9 9 + 17 > FH FH > 8 This can be written “ 8 < FH. ” FH > – 8 26 > FH This can be written “FH < 26. ” The length of FH must be longer than 8 m and shorter than 26 m. 5 -5

Inequalities in Triangles GEOMETRY LESSON 5 -5 Pages 276 -279 Exercises 1. 2. 3 2 because they are vertical s and m 1 > m 3 by Corollary to the Ext. Thm. So, m 1 > m 2 by subst. 3. (continued) lines, then alt. int. are. s 11. FH, GF, GH 12. TU, UV, TV 4. M, L, 5. D, C, E 13. AC, AB, CB An ext. of a is larger than either remote int. . 6. G, H, I 14. EF, DE, DF 7. A, B, C 15. ZY, XZ, XY m 1 > m 4 by Corollary to the Ext. Thm. and 4 2 because if 8. E, F, D 16. No; 2 + 3 > 6. 9. Z, X, Y 17. Yes; 11 + 12 > 15; 12 + 15 > 11; 11 + 15 > 12 5 -5 K 10. MN, ON, MO

Inequalities in Triangles GEOMETRY LESSON 5 -5 18. No; 8 + 10 > 19. 23. 11 < s < 21 19. Yes; 1 + 15 > 15; 15 + 15 > 11. 24. 0 < s < 12 25. 15 < s < 41 20. Yes; 2 + 9 > 10; 9 + 10 > 2; 2 + 10 > 9. 26. 3 < s < 11 27. 15 < s < 55 21. No; 4 + 5 > 9. 22. 4 < s < 20 28. Answers may vary. Sample: If Y is the distance between Wichita and Topeka, then 20 < Y < 200. 5 -5 29. Let the distance between the peaks be d and the distances from the hiker to each of the peaks be a and b. Then d + a > b and d + b > a. Thus, d > b – a and d > a –b.

Inequalities in Triangles GEOMETRY LESSON 5 -5 30. a. 33. a. m OTY b. m 3 b. the third side of the 1 st third side of the 2 nd. is longer than the c. Base isosc. d. s of an are. Add. Post. See diagram in part (a). The included the included of the first is greater than of the second. e. Comparison Prop. of Ineq. f. Subst. (step 2) 31. Answers may vary. Sample: The shortcut across the grass is shorter than the sum of the two paths. 32. AB 5 -5 g. An ext. of a is greater than either remote int. .

Inequalities in Triangles GEOMETRY LESSON 5 -5 33. (continued) h. Trans. Prop. of Ineq. 39. 5 18 40. 34. RS 35. CD CD = AC was given so ACD is isosc. By def. of isos. . This means m D = m CAD. Then m DAB > m CAD by the Comparison Prop. of Ineq. So by subst. , m DAB > m D and by Thm. 5 -11 DB > AB. Since DC + CB = DB, by subst. DC + CB > AB. Using subst. again, AC + CB > AB. 36. XY 37. 1 2 38. (2, 4), (2, 5), (2, 6), (3, 3), (3, 4), (3, 6), (3, 7), (4, 3), (4, 4), (4, 5), (4, 6), (4, 7), (4, 8) 41. T is the largest in PTA. Thus PA > PT because the longest side of a is opp. The largest. 5 -5

Inequalities in Triangles GEOMETRY LESSON 5 -5 42. D 43. A 44. B 47. [2] a. Since m A > m C > m B, the sides opp. them are related in the same way: BC > AB > AC. Of AB and AC, AB is longer than AC. Since 9 in. > 5 in. , AB = 9 in. and AC = 5 in. 45. C b. BC is the longest side, so 9 < BC < 14. The possible whole number measures for BC are 10 in. , 11 in. , 12 in. , and 13 in. 46. B [1] part (a) OR part (b) incorrect 48. m A>m B 49. m X≤m B 50. The angle is not a right angle. 5 -5

Inequalities in Triangles GEOMETRY LESSON 5 -5 51. The triangle is obtuse. 59. 314. 2 mi 2 52. 90 53. 35 54. 145 55. 55 56. 8. 0 ft 2 57. 962. 1 mm 2 58. 0. 8 m 2 5 -5

Inequalities in Triangles GEOMETRY LESSON 5 -5 Use the figure for Exercises 1– 3. 1. Explain why m 4 > m 1 by the Corollary to the Exterior Angle Theorem. 2. Explain why m 3 > m 1. By Theorem 5 -10, if two sides are not congruent, the larger angle lies opposite the longer side, so m 3 > m 1. 3. Use ABC to describe the possible lengths of AC. 13 < AC < 37 4. Can a triangle have lengths of 2 mm, 3 mm, and 6 mm? Explain. no; 2 + 3 >/ 6 5. In XYZ, XY = 5, YZ = 8, and XZ = 7. Which angle is largest? X 6. In PQT, m P = 50 and m T = 70. Which side is shortest? QT 5 -5

Relationships Within Triangles GEOMETRY CHAPTER 5 Page 284 1. 2. a. If a polygon does not have 8 sides, then it is not an octagon. 2. b. (continued) even-numbered year, then it is not a leap year. 4. (continued) Midsegment Thm. b. If a polygon is not an octagon, then it does not have 8 sides. 3. a. If it is not snowing, then it is summer. 6. II and III a. If it is not a leap year, then it is not an evennumbered year. b. If it is not an b. If it is summer, then it is not snowing. 5. I and II 7. A, C, B 8. B, C, A 9. C, B, A 4. Answers may vary. 1 Sample: DE = 2 BC and DE BC by 5 -A 10. Answers may vary. Sample: 2, 4, 8 because 2 + 4 > 8

Relationships Within Triangles GEOMETRY CHAPTER 5 11. ST, SR, RT 12. KV, VM, KM 13. 6. 5 14. 12 15. Assume that the obtuse is a base. Then by def. of an isos. , the other base must be obtuse since they are. Since each would have measure greater 15. (continue) than 90, their sum would be greater than 180. This contradicts the Sum Thm. , so the obtuse must be the vertex. 20. 1 , – 4 1 2 2 21. circumcenter 22. a. QA b. QA c. Trans. Prop. of = 16. 7; 27 17. 2 ; 8 3 18. 3 – 2 1 , – 1 1 2 2 19. (– 2, 1) 23. Y is on TW, the bis. of XZ; Y is equidistant from X and Z. 24. A is on CK; Conv. of the Bis. Thm. 5 -A