5 1 Midsegments of Triangles Midsegment connects the

  • Slides: 9
Download presentation
5. 1 Midsegments of Triangles -Midsegment: connects the midpoint of two sides -Theorem 5.

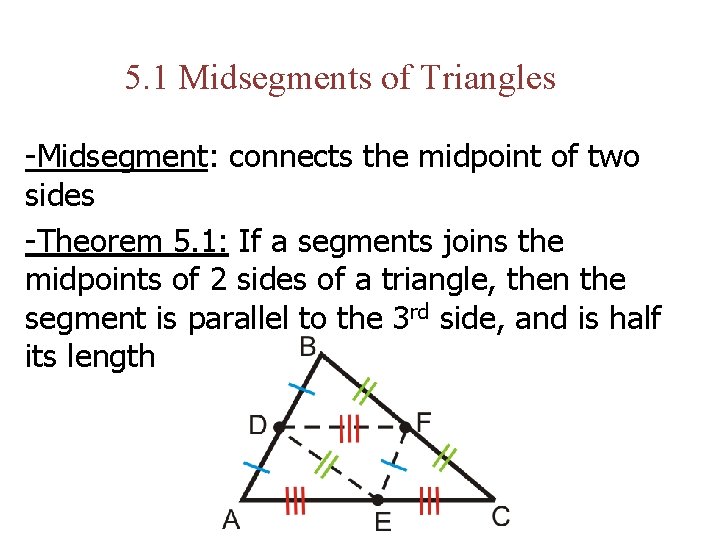
5. 1 Midsegments of Triangles -Midsegment: connects the midpoint of two sides -Theorem 5. 1: If a segments joins the midpoints of 2 sides of a triangle, then the segment is parallel to the 3 rd side, and is half its length

5. 2 Perpendicular and angle bisectors -Theorem 5. 4: If a point is on

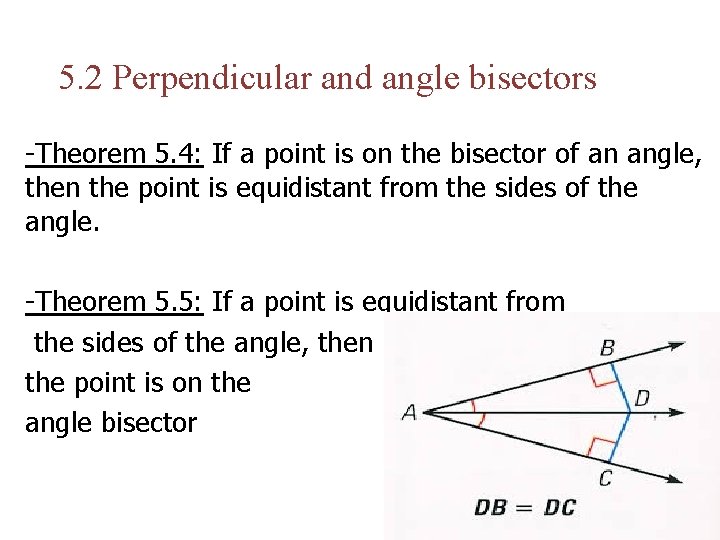
5. 2 Perpendicular and angle bisectors -Theorem 5. 4: If a point is on the bisector of an angle, then the point is equidistant from the sides of the angle. -Theorem 5. 5: If a point is equidistant from the sides of the angle, then the point is on the angle bisector

5. 3 bisectors in triangles -Theorem 5. 6: The perpendicular bisectors of the sides

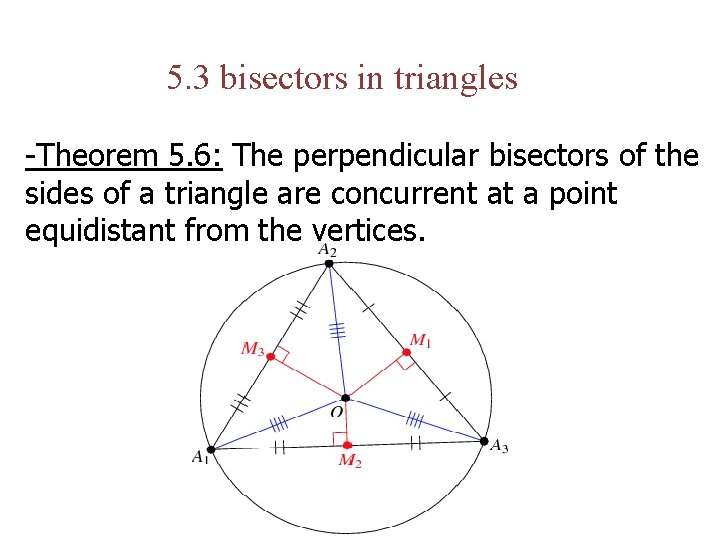
5. 3 bisectors in triangles -Theorem 5. 6: The perpendicular bisectors of the sides of a triangle are concurrent at a point equidistant from the vertices.

5. 3 bisectors in triangles -Circumcenter: Point of concurrency of perpendicular bisectors of a

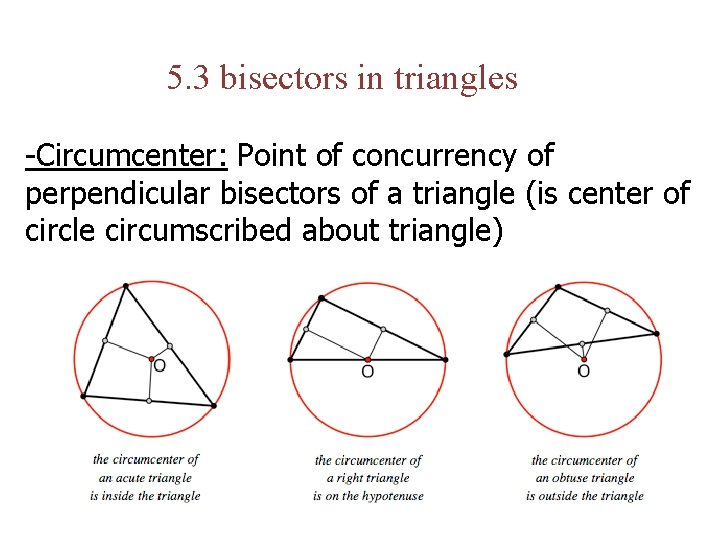
5. 3 bisectors in triangles -Circumcenter: Point of concurrency of perpendicular bisectors of a triangle (is center of circle circumscribed about triangle)

5. 3 bisectors in triangles -Theorem 5. 7: The bisectors of the angles of

5. 3 bisectors in triangles -Theorem 5. 7: The bisectors of the angles of a triangle are concurrent at a point equidistant from the Sides of the triangle. -Incenter: Point of concurrency of the angle bisectors of a triangle (is center of circle inscribed in triangle)

5. 4 Medians and altitudes -Theorem 5. 8: The medians of a triangle are

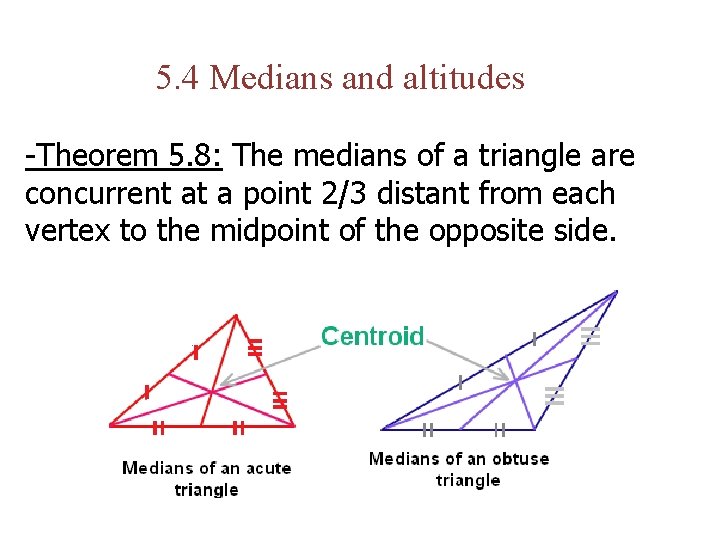
5. 4 Medians and altitudes -Theorem 5. 8: The medians of a triangle are concurrent at a point 2/3 distant from each vertex to the midpoint of the opposite side.

5. 4 Medians and altitudes -Altitude: perpendicular segment from a vertex of a triangle

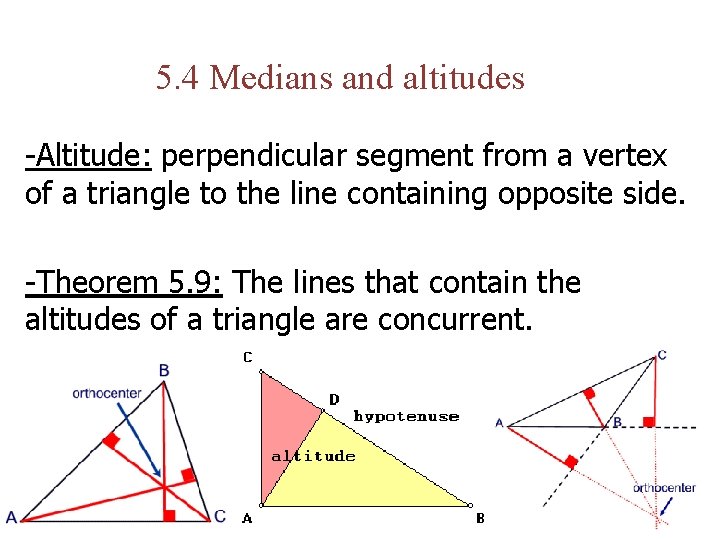
5. 4 Medians and altitudes -Altitude: perpendicular segment from a vertex of a triangle to the line containing opposite side. -Theorem 5. 9: The lines that contain the altitudes of a triangle are concurrent.

5. 5 Indirect Reasoning -Indirect Reasoning: All possibilities are considered and then all but

5. 5 Indirect Reasoning -Indirect Reasoning: All possibilities are considered and then all but one are proved false -Indirect proof: state an assumption as the opposite of what you’re trying to prove. Show the assumption leads to a contradiction, therefore proving your assumption false and what you wanted true

5. 6 Inequalities in triangles -Comparison Property of Inequality: If a = b +

5. 6 Inequalities in triangles -Comparison Property of Inequality: If a = b + c and c > 0, then a > b -Corollary to Triangle Exterior Angle Theorem: The exterior angle of a triangle is greater than either of its remote interior angles -Theorem 5. 10: If 2 sides of a triangle are not congruent, then the larger angle lies opposite the longer side -Theorem 5. 11: If 2 angles of a triangle are not congruent, then the longer side lies opposite the larger angle -Theorem 5. 12: The Triangle Inequality Theorem says the sum of 2 legs of any 2 sides of a triangle is greater than the length of the 3 rd side

Midsegments of Triangles A midsegment of a triangleMidsegments of Triangles A midsegment of a triangle
MIDSEGMENT THEOREM OBJECTIVE To use properties of midsegmentsMIDSEGMENT THEOREM OBJECTIVE To use properties of midsegments
5 4 Midsegment Theorem Using Midsegments of a5 4 Midsegment Theorem Using Midsegments of a
Lesson 5 4 Prove Midsegment Theorem Use MidsegmentLesson 5 4 Prove Midsegment Theorem Use Midsegment
Triangle Segments Triangle Midsegment A midsegment of aTriangle Segments Triangle Midsegment A midsegment of a
Midsegment of a triangle Midsegment of a triangleisMidsegment of a triangle Midsegment of a triangleis
5 4 The Triangle Midsegment Theorem Vocabulary midsegment5 4 The Triangle Midsegment Theorem Vocabulary midsegment
Triangle Midsegment Theorem 6 4 A midsegment ofTriangle Midsegment Theorem 6 4 A midsegment of