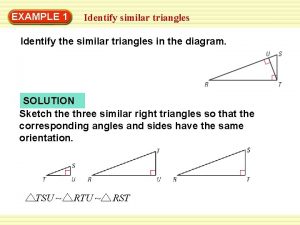
Similar Triangles Identify Similar Triangles Triangles are similar

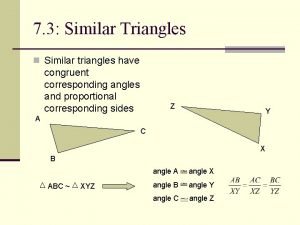
Similar Triangles

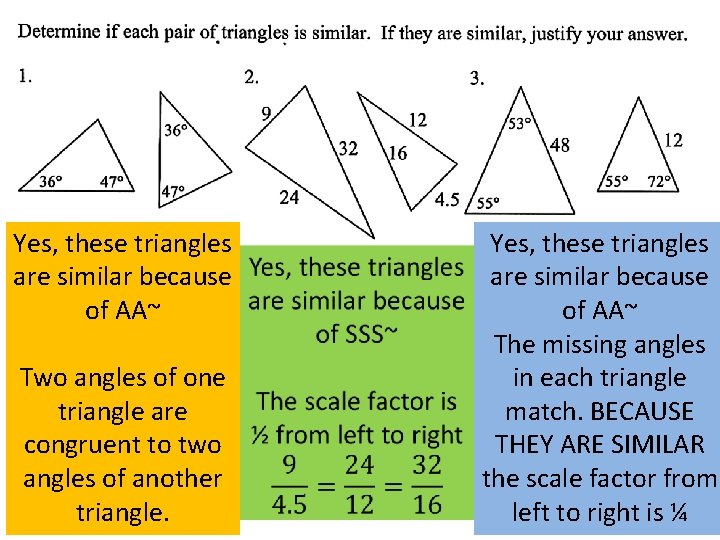
Identify Similar Triangles: Triangles are similar if they have the same shape, but have different sizes. We saw this happen with dilations! If two figures are similar, you should be able to identify the scale factor! SSS~ AA~ SAS~ The measures of the corresponding side lengths of two triangles are proportional. Two angles of one triangle are congruent to two angles of another triangle. The measures of two side lengths of one triangle are proportional to the measures of two corresponding side lengths of another triangle, and the included angles are congruent.

“How do you know if two triangles are similar? ”

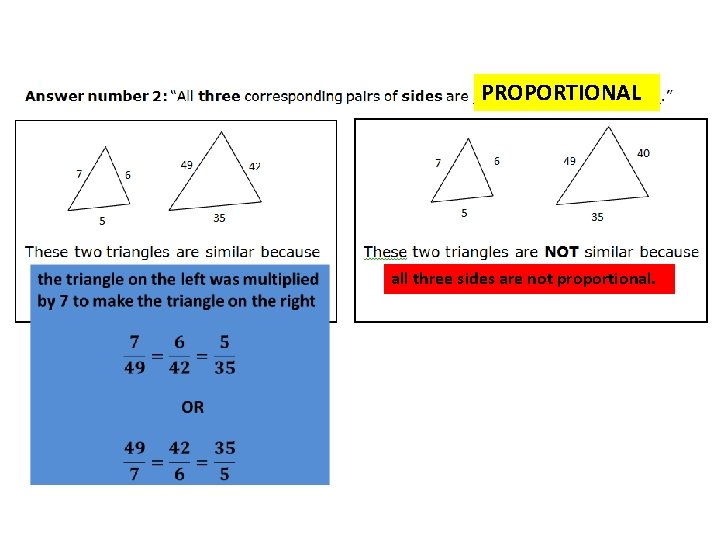
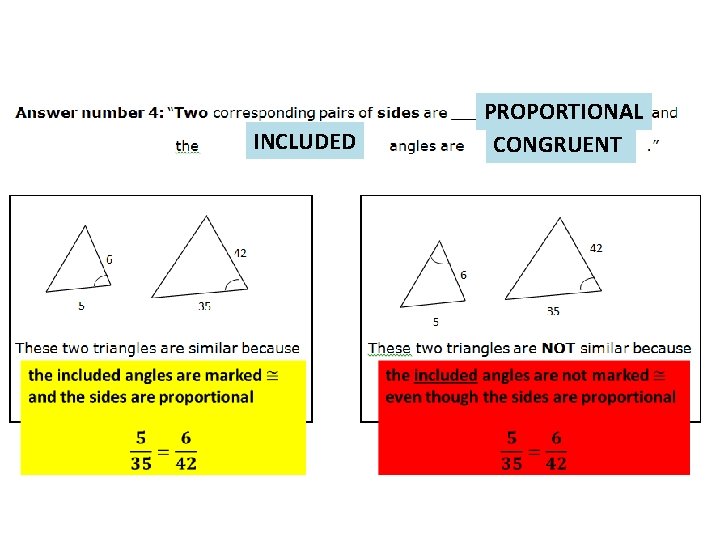
PROPORTIONAL all three sides are not proportional.

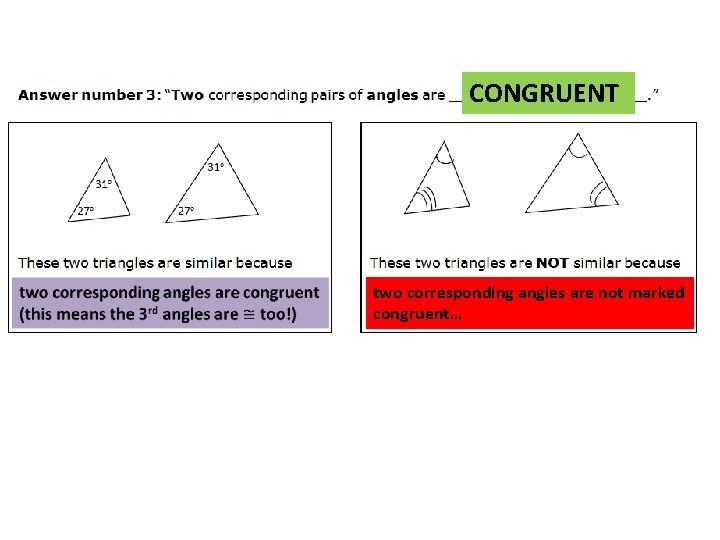
CONGRUENT two corresponding angles are not marked congruent…

PROPORTIONAL CONGRUENT INCLUDED

Yes, these triangles are similar because of AA~ Two angles of one triangle are congruent to two angles of another triangle. Yes, these triangles are similar because of AA~ The missing angles in each triangle match. BECAUSE THEY ARE SIMILAR the scale factor from left to right is ¼

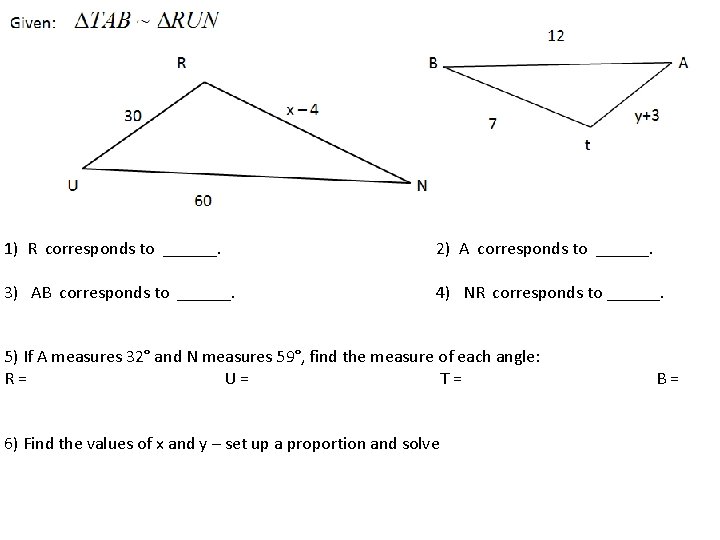
1) R corresponds to ______. 2) A corresponds to ______. 3) AB corresponds to ______. 4) NR corresponds to ______. 5) If A measures 32° and N measures 59°, find the measure of each angle: R = U = T = 6) Find the values of x and y – set up a proportion and solve B =

7) The scale on a map is 2 cm: 25 miles. The distance between two cities on the map is 7 cm. What is the actual distance between the cities? 8) A man stands next to a tree. He is 6 feet tall and his shadow measures 9 feet. If the tree has a shadow measuring 43 feet, how tall is the tree? 9) A rectangular photograph is 8 in wide and 10 in tall. It must be enlarged so it can be placed on a poster, and it must be 34 in wide. How tall should the enlarged photograph be?