Similarity and Using Similar Triangles Similar Figures Similar

Similarity and Using Similar Triangles

Similar Figures �Similar figures have the same shape, but different size. �The angles and side lengths will correspond just as they did in congruent figures, BUT… �The corresponding side lengths will not be congruent. They will be proportional �The corresponding angles will remain congruent

Similar Polygons �To produce similar polygons, a dilation must have occurred (along with other possible transformations as well) �Write down which vertices in quadrilateral ABCD correspond to which PQRS. S R vertices in quadrilateral The arrow “→” means. Q“corresponds to. ” P �A → B→ �C → D→ S R �The corresponding angles REMAIN CONGRUENT!! � C � A P D B Q

Similar Polygons �To produce similar polygons, a dilation must have occurred �The side lengths will be a new size, but they 3 will be proportional according to the scale factor. 4 2 �Write down the corresponding side lengths 5 RS �AB → PQ �CD→ SP BC → QR 9 DA → �The corresponding. Image side lengths side are=proportional the scale length set up a fraction factor RS 6 15 12 = 3 (the pre-image scaleside factor) 12 = AB 4 length PQ = 6 = 3 SP = 9 = 3 QR= 15= 3 ALL corresponding side lengths need to be 5 DA 3 BC CD 2 proportional

Are the two figures similar? 9 cm �Measure parts of both figures. �How do we use these numbers to determine if the figures are similar? �Find the scale factor. � 8 ÷ 24 = 1/3 � 3 ÷ 9 = 1/3 �Since the scale factor is the same for both sets of sides, the figures are similar. 24 cm 3 cm 8 cm

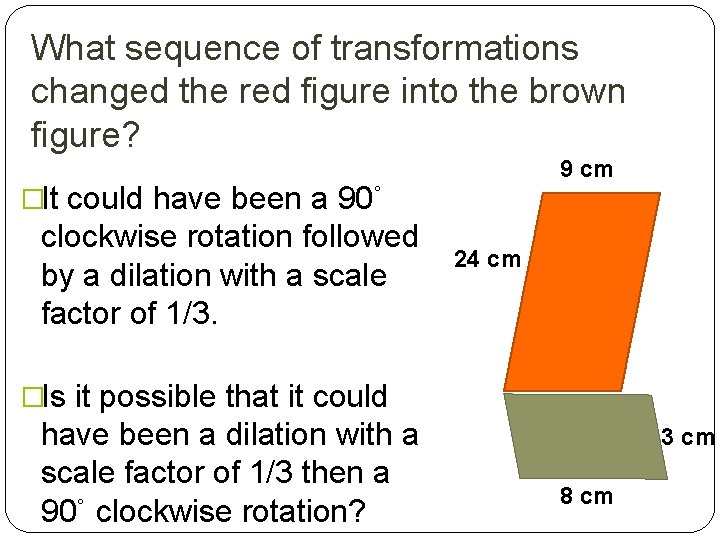
What sequence of transformations changed the red figure into the brown figure? 9 cm �It could have been a 90˚ clockwise rotation followed by a dilation with a scale factor of 1/3. 24 cm �Is it possible that it could have been a dilation with a scale factor of 1/3 then a 90˚ clockwise rotation? 3 cm 8 cm

Similar Triangles �Similar triangles have the same shape, but different size. �You can use the relationships between corresponding parts of similar triangles to solve measurement problems.

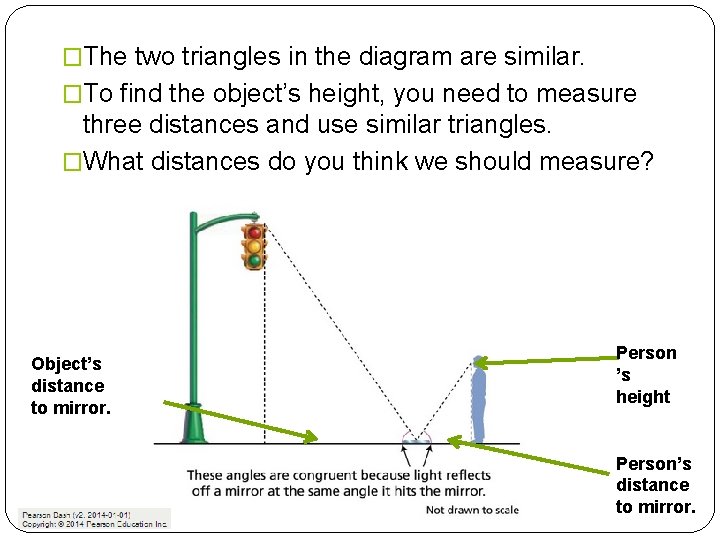
�The two triangles in the diagram are similar. �To find the object’s height, you need to measure three distances and use similar triangles. �What distances do you think we should measure? Object’s distance to mirror. Person ’s height Person’s distance to mirror.

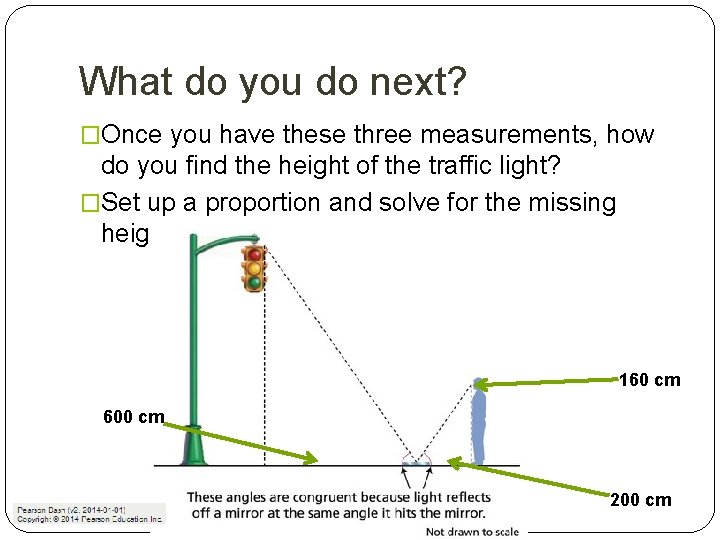
What do you do next? �Once you have these three measurements, how do you find the height of the traffic light? �Set up a proportion and solve for the missing height. 160 cm 600 cm 200 cm

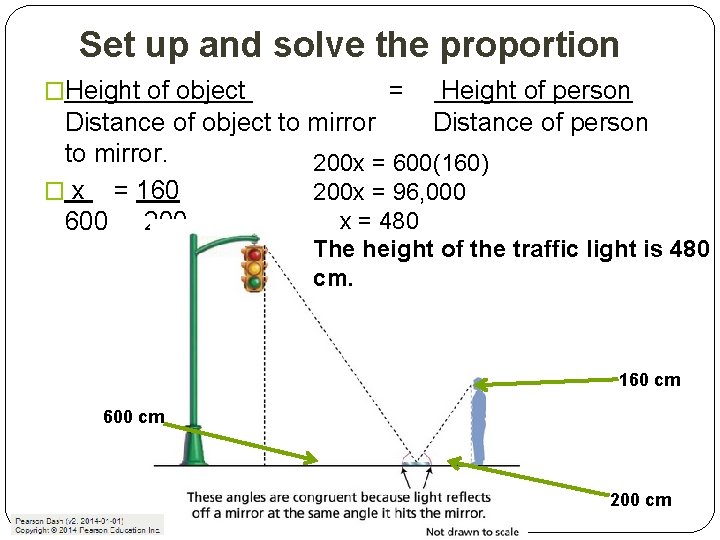
Set up and solve the proportion �Height of object = Height of person Distance of object to mirror. 200 x = 600(160) � x = 160 200 x = 96, 000 x = 480 600 200 The height of the traffic light is 480 cm. 160 cm 600 cm 200 cm