7 3 Similar Triangles n Similar triangles have


- Slides: 12

7. 3: Similar Triangles n Similar triangles have congruent corresponding angles and proportional corresponding sides Z Y A C X B ABC ~ XYZ angle A angle X angle B angle Y angle C angle Z

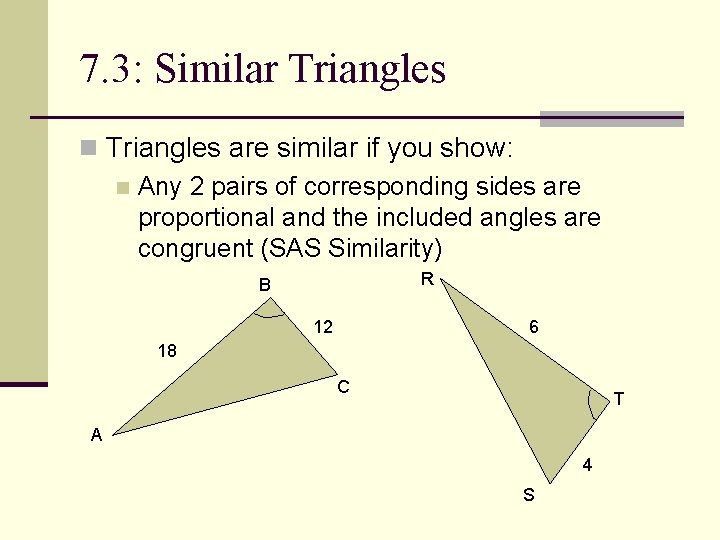
7. 3: Similar Triangles n Triangles are similar if you show: n Any 2 pairs of corresponding sides are proportional and the included angles are congruent (SAS Similarity) R B 12 6 18 C T A 4 S

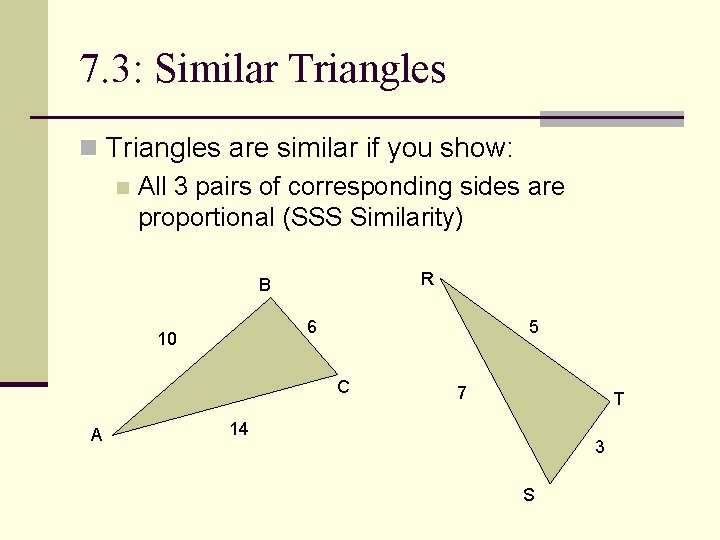
7. 3: Similar Triangles n Triangles are similar if you show: n All 3 pairs of corresponding sides are proportional (SSS Similarity) R B 6 10 5 C A 7 T 14 3 S

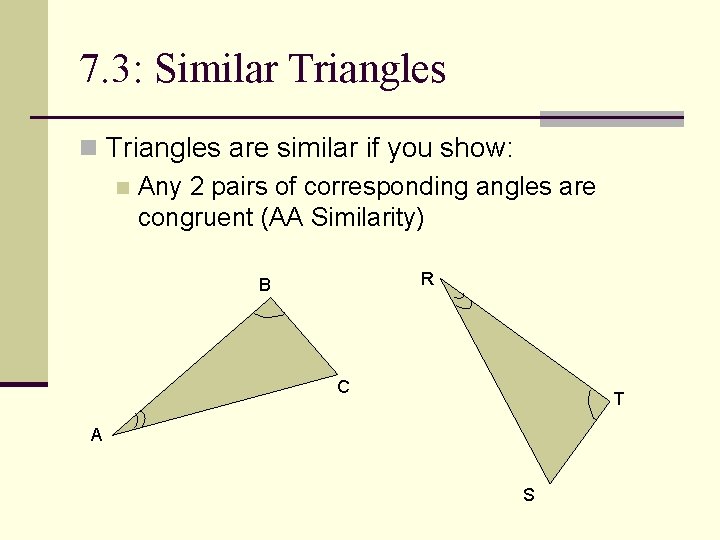
7. 3: Similar Triangles n Triangles are similar if you show: n Any 2 pairs of corresponding angles are congruent (AA Similarity) R B C T A S

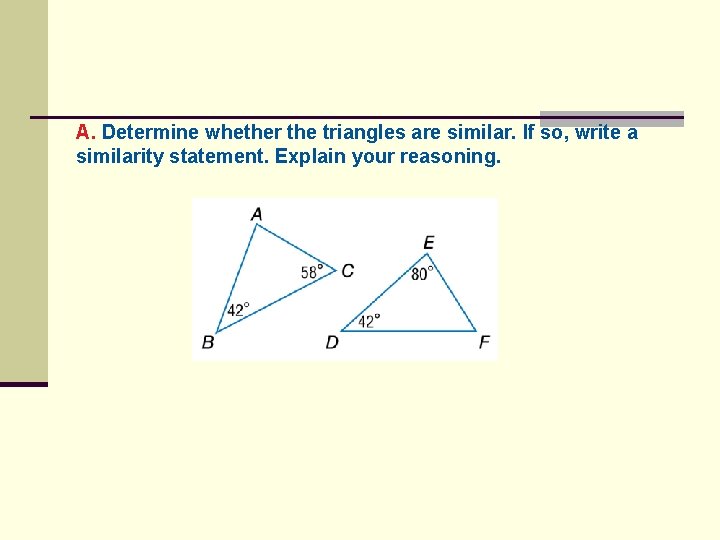
A. Determine whether the triangles are similar. If so, write a similarity statement. Explain your reasoning.

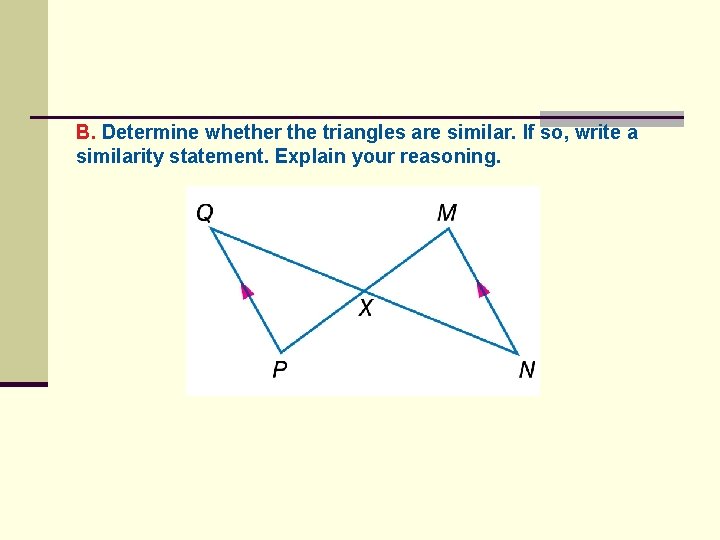
B. Determine whether the triangles are similar. If so, write a similarity statement. Explain your reasoning.

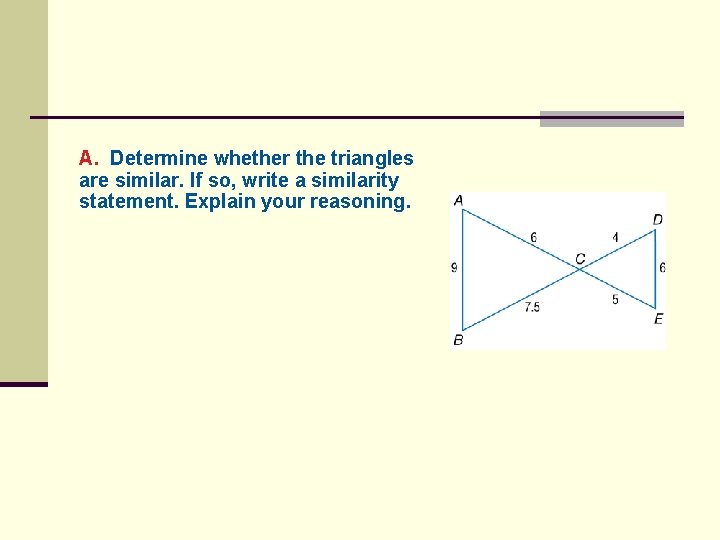
A. Determine whether the triangles are similar. If so, write a similarity statement. Explain your reasoning.

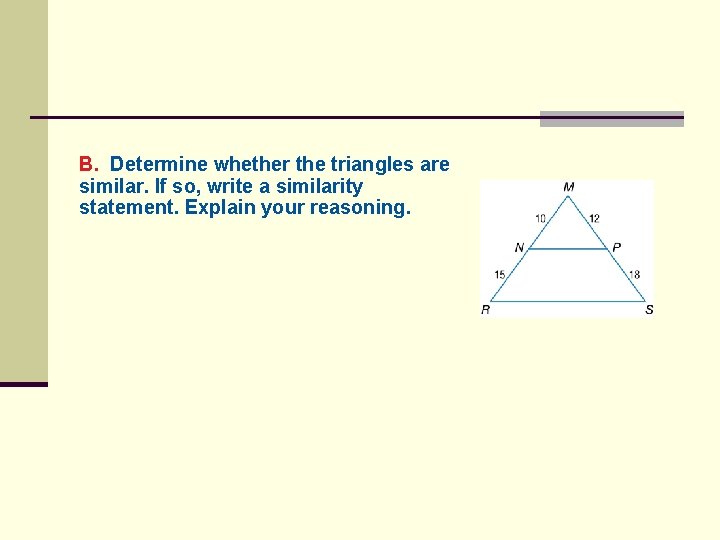
B. Determine whether the triangles are similar. If so, write a similarity statement. Explain your reasoning.

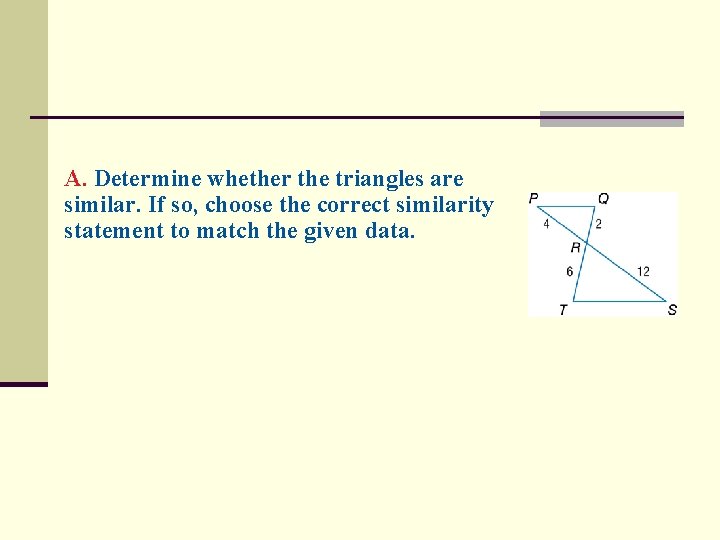
A. Determine whether the triangles are similar. If so, choose the correct similarity statement to match the given data.

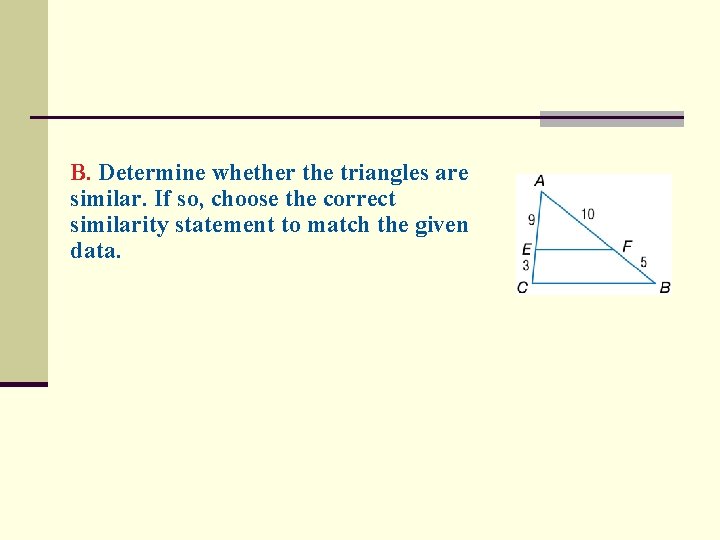
B. Determine whether the triangles are similar. If so, choose the correct similarity statement to match the given data.

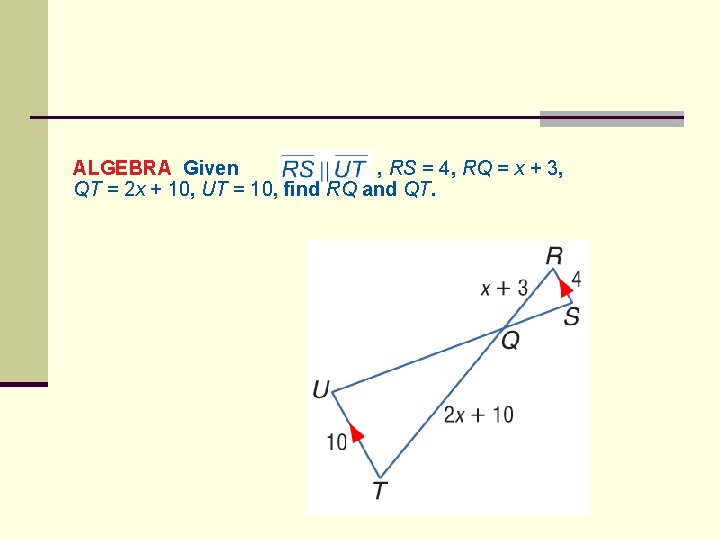
ALGEBRA Given , RS = 4, RQ = x + 3, QT = 2 x + 10, UT = 10, find RQ and QT.

SKYSCRAPERS Josh wanted to measure the height of the Sears Tower in Chicago. He used a 12 -foot light pole and measured its shadow at 1 p. m. The length of the shadow was 2 feet. Then he measured the length of the Sears Tower’s shadow and it was 242 feet at the same time. What is the height of the Sears Tower?
 What shape has 8 vertices 12 edges and 6 flat faces
What shape has 8 vertices 12 edges and 6 flat faces Precipitancy creates prodigality
Precipitancy creates prodigality Similar disuelve a similar
Similar disuelve a similar Propiedades fisicoquímicas del agua
Propiedades fisicoquímicas del agua Similar disuelve a similar
Similar disuelve a similar Similar triangles and trigonometry
Similar triangles and trigonometry Similar triangles
Similar triangles Solve for x. the triangles are similar.
Solve for x. the triangles are similar. Vedf
Vedf Chapter 7 geometry vocab
Chapter 7 geometry vocab Prove sss similarity theorem
Prove sss similarity theorem Identifying similar triangles
Identifying similar triangles Identify similar triangles worksheet
Identify similar triangles worksheet