9 3 Similar Triangles 9 3 Similar Triangles

9 -3: Similar Triangles

9 -3: Similar Triangles • Back in Chapter 5, we talked postulates for triangle congruence ▫ ▫ SSS SAS ASA AAS (Side-Side) (Side-Angle-Side) (Angle-Side-Angle) (Angle-Side) • The only two triangle congruence statements that didn’t work were AAA and ASS. • When talking about similarity, one of them does work

9 -3: Similar Triangles • AA Similarity: If two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar. • The rest of our postulates can be applied for similarity ▫ SSS Similarity ▫ SAS Similarity �ASA Similarity & AAS Similarity fall under AA Similarity

9 -3: Similar Triangles • Example #1 ▫ Determine whether the two triangles are similar. If so, tell which similarity test is used and complete the statement. � JMP GHK ~ _____ Because 6/ = 10/ 9 15 = 14/ 21 These triangles have SSS Similarity

9 -3: Similar Triangles • Example #2 ▫ Find the value of x �Sometimes, it helps to rotate/flip an image to better see how the parts correspond. � 9/ = x/ 3 5 � 3 x = 45 �x = 15 9 12

9 -3: Similar Triangles • YOUR TURN ▫ Determine if the triangles are similar. If so, tell which similarity test and complete the statement DGH ~ _____ ▫ Not similar

9 -3: Similar Triangles • Your Turn #2 ▫ Find the values of x and y if the triangles are similar. �x = 36 �y = 39

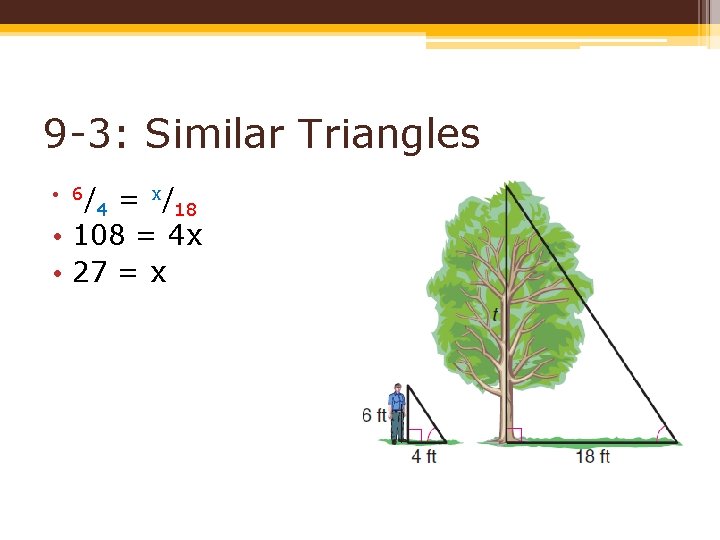
9 -3: Similar Triangles • Similar Triangles can be used to measure things that otherwise could prove to be difficult. ▫ Example: A tree casts a shadow of 18 feet long. If you are 6 feet tall and cast a 4 foot shadow, how tall is the tree? �DRAW A DIAGRAM!!! (next slide)

9 -3: Similar Triangles • 6/ = x/18 • 108 = 4 x • 27 = x 4

9 -3: Similar Triangles • Assignment ▫ Worksheet #9 -3