Proving Similar Triangles 7 3 Remember Similar triangles

Proving Similar Triangles 7. 3

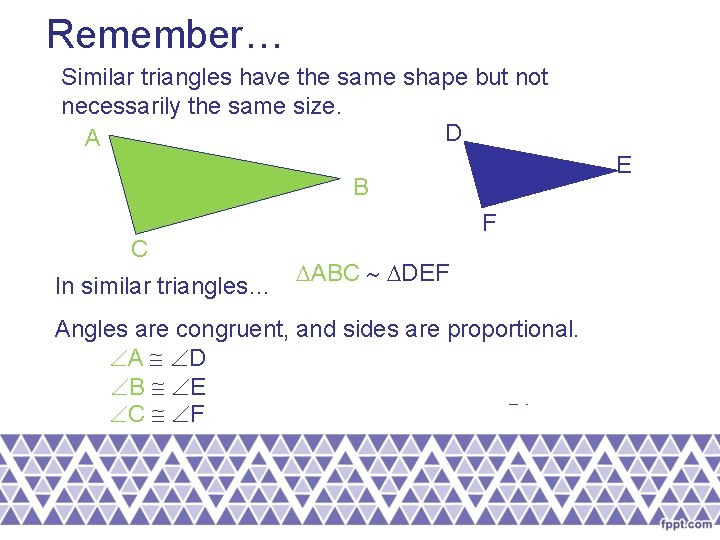
Remember… Similar triangles have the same shape but not necessarily the same size. D A B C In similar triangles… F ABC DEF Angles are congruent, and sides are proportional. A D AB BC AC = = B E DE EF DF C F E

Proving Similar Triangles There are three ways to prove triangles are similar. 1. SSS Similarity Theorem 3 pairs of proportional sides 2. SAS Similarity Theorem 2 pairs of proportional sides and congruent angles between them 3. AA Similarity Theorem 2 pairs of congruent angles

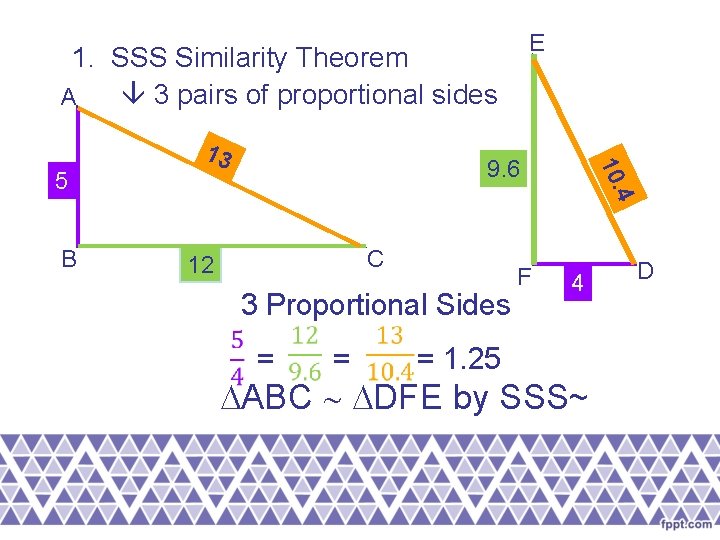
E 1. SSS Similarity Theorem 3 pairs of proportional sides A 4 B 9. 6 10. 5 13 C 12 3 Proportional Sides = = = 1. 25 F 4 ABC DFE by SSS~ D

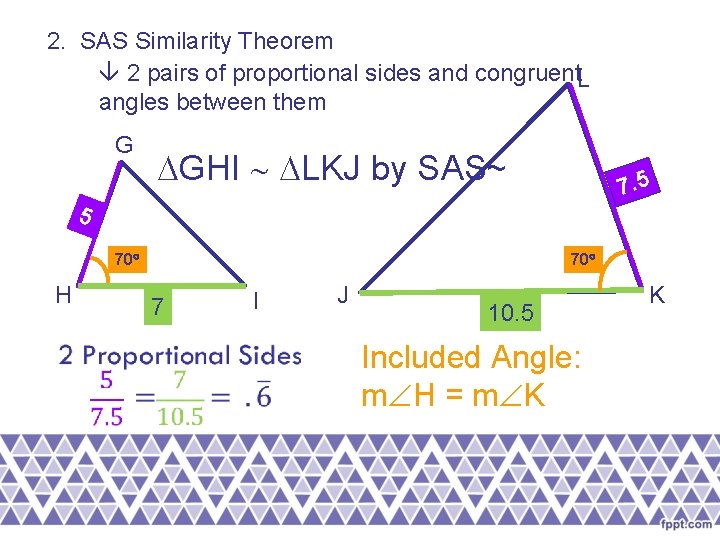
2. SAS Similarity Theorem 2 pairs of proportional sides and congruent. L angles between them G GHI LKJ by SAS~ 7. 5 5 70 H 70 7 I J 10. 5 Included Angle: m H = m K K

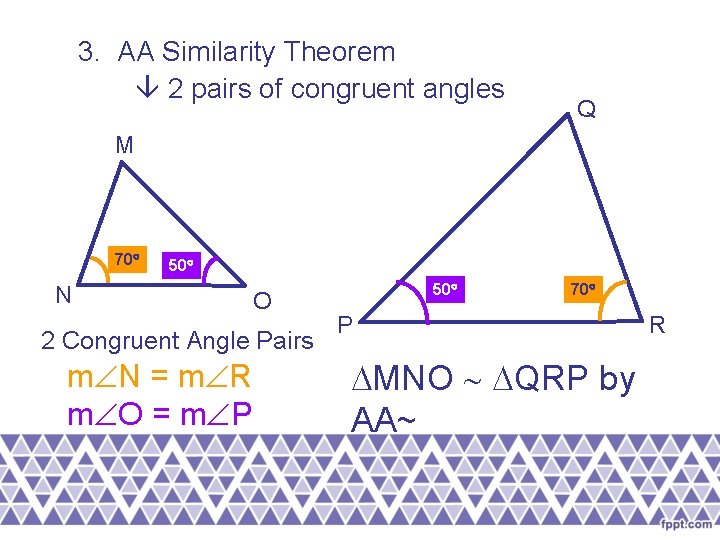
3. AA Similarity Theorem 2 pairs of congruent angles Q M 70 50 N O 2 Congruent Angle Pairs m N = m R m O = m P 50 70 P MNO QRP by AA~ R

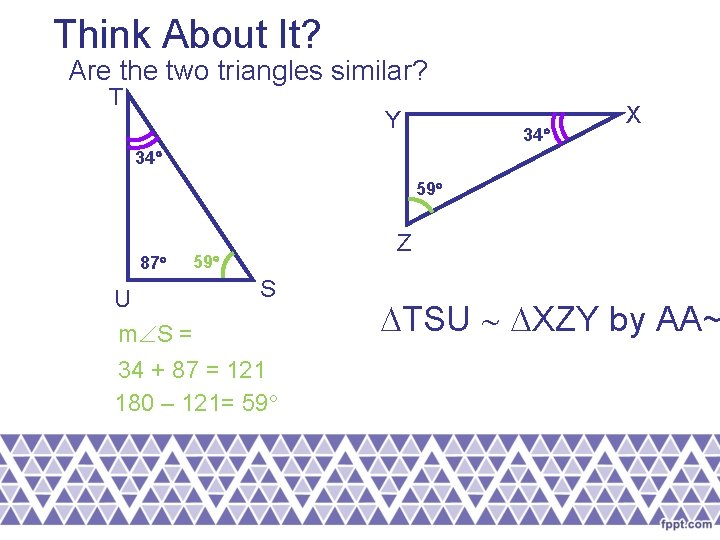
Think About It? Are the two triangles similar? T Y 34 X 34 59 87 Z 59 U m S = S 34 + 87 = 121 180 – 121= 59 TSU XZY by AA~

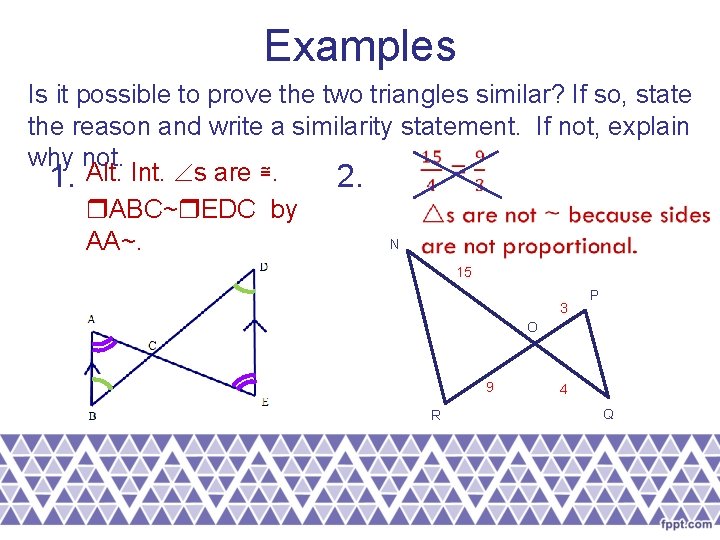
Examples Is it possible to prove the two triangles similar? If so, state the reason and write a similarity statement. If not, explain why not. 1. Alt. Int. s are ≅. 2. ABC~ EDC by N AA~. 15 3 P O 9 R 4 Q

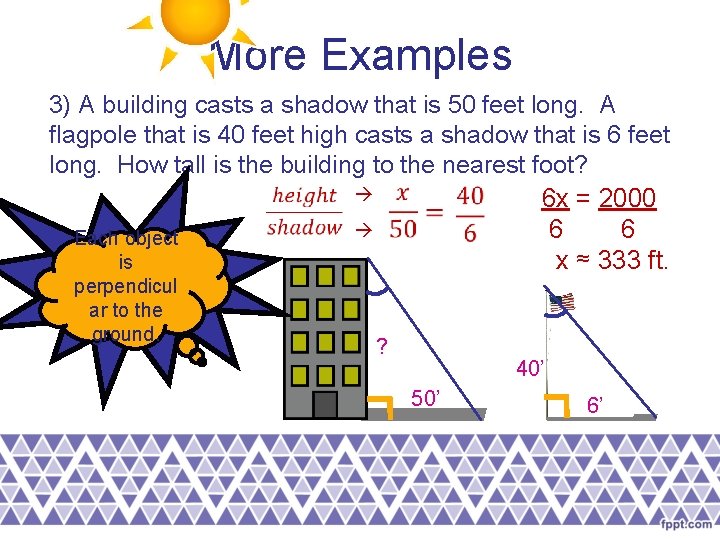
More Examples 3) A building casts a shadow that is 50 feet long. A flagpole that is 40 feet high casts a shadow that is 6 feet long. How tall is the building to the nearest foot? 6 x = 2000 6 6 Each object The sun is makes x ≈ 333 ft. the same angle perpendicul withareach object. to the ground. ? 40’ 50’ 6’

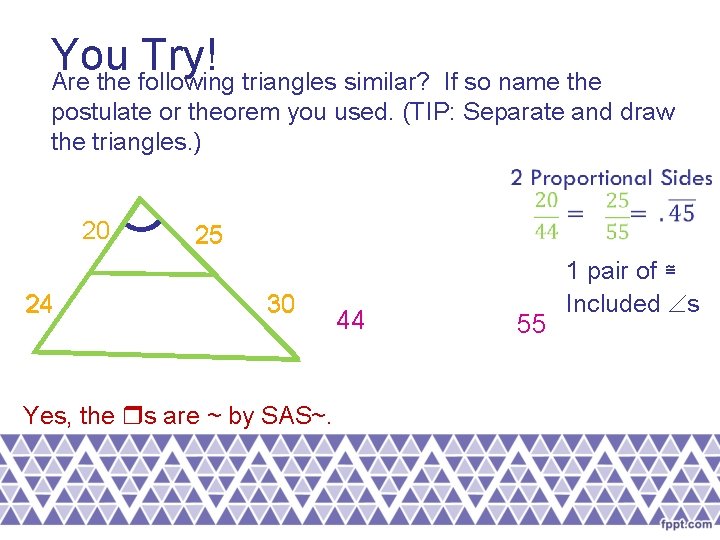
You Try! Are the following triangles similar? If so name the postulate or theorem you used. (TIP: Separate and draw the triangles. ) 20 24 25 30 Yes, the s are ~ by SAS~. 44 55 1 pair of ≅ Included s

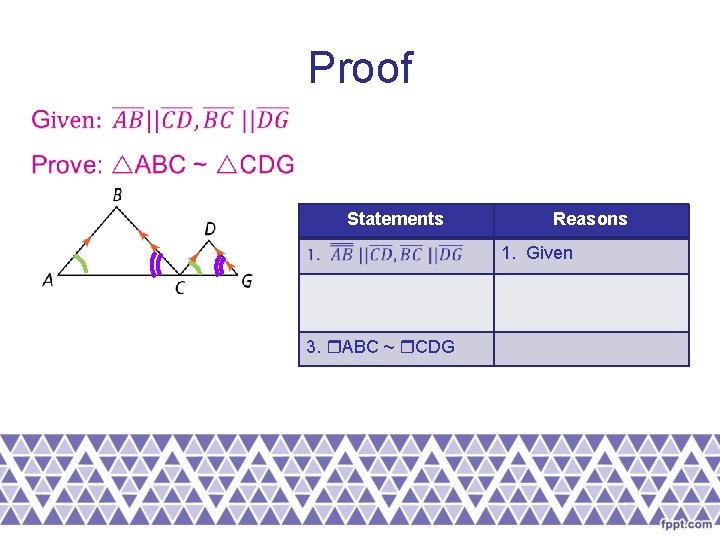
Proof Statements Reasons 1. Given 2. A ≅ DCG BCA ≅ DGC 2. Corresponding Thm. 3. ABC ~ CDG 3. AA ~ Thm