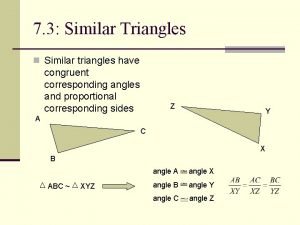
6 5 Prove Triangles Similar by SSS and

6. 5 – Prove Triangles Similar by SSS and SAS Geometry Ms. Rinaldi

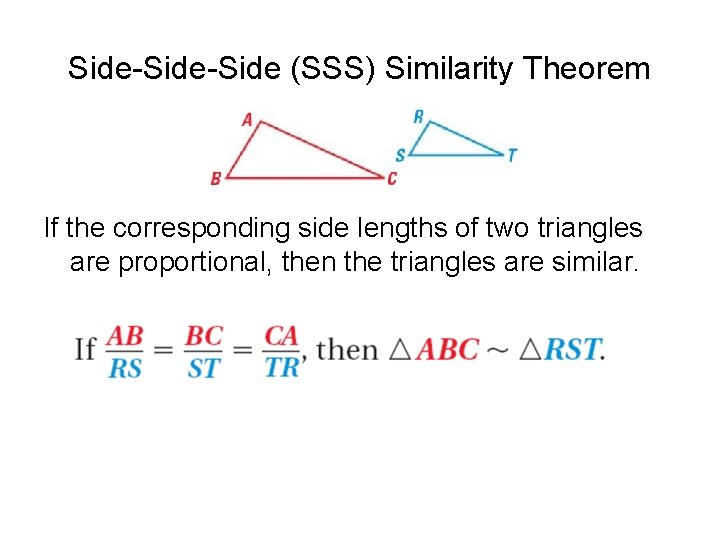
Side-Side (SSS) Similarity Theorem If the corresponding side lengths of two triangles are proportional, then the triangles are similar.

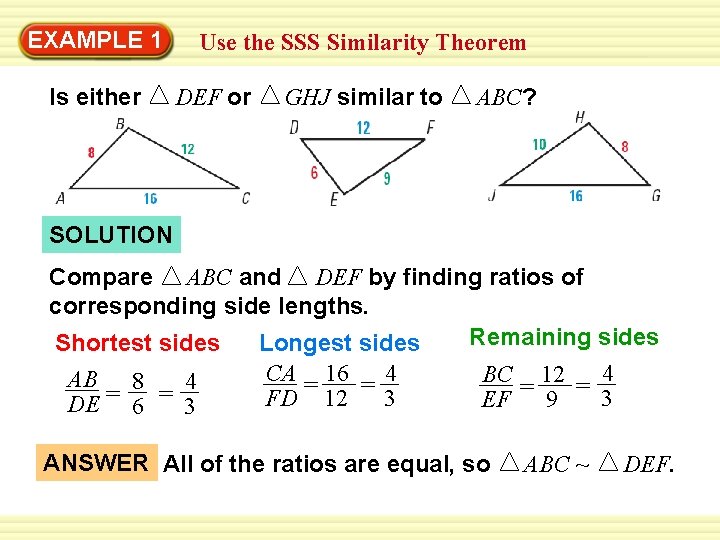
EXAMPLE 1 Is either Use the SSS Similarity Theorem DEF or GHJ similar to ABC? SOLUTION Compare ABC and DEF by finding ratios of corresponding side lengths. Remaining sides Shortest sides Longest sides CA = 16 = 4 BC 12 = 4 AB 8 4 = = = 3 3 FD 12 EF 9 DE 6 3 ANSWER All of the ratios are equal, so ABC ~ DEF.

EXAMPLE 1 Use the SSS Similarity Theorem (continued) Compare ABC and GHJ by finding ratios of corresponding side lengths. Shortest sides AB 8 1 GH = 8 = Longest sides Remaining sides CA 16 1 JG = 16 = BC 12 = 6 = HJ 10 5 ANSWER The ratios are not all equal, so not similar. ABC and GHJ are

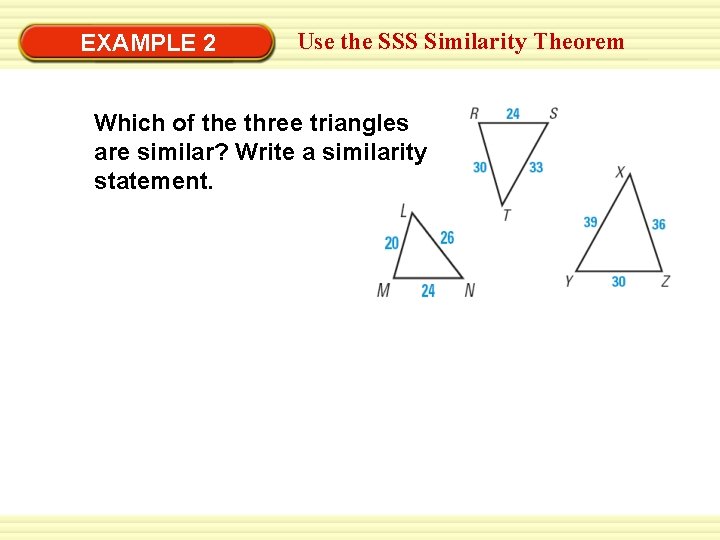
EXAMPLE 2 Use the SSS Similarity Theorem Which of the three triangles are similar? Write a similarity statement.

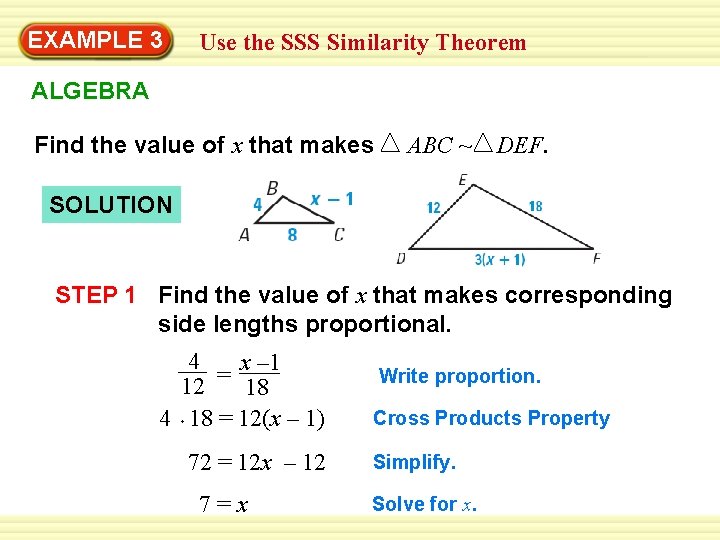
EXAMPLE 3 Use the SSS Similarity Theorem ALGEBRA Find the value of x that makes ABC ~ DEF. SOLUTION STEP 1 Find the value of x that makes corresponding side lengths proportional. 4 x – 1 = 12 18 4 18 = 12(x – 1) 72 = 12 x – 12 7=x Write proportion. Cross Products Property Simplify. Solve for x.

EXAMPLE 3 Use the SSS Similarity Theorem (continued) STEP 2 Check that the side lengths are proportional when x = 7. DF = 3(x + 1) = 24 BC = x – 1 = 6 AB ? BC DE = EF 6 4 12 = 18 AB ? AC DE = DF 8 4 = 12 24 ANSWER When x = 7, the triangles are similar by the SSS Similarity Theorem.

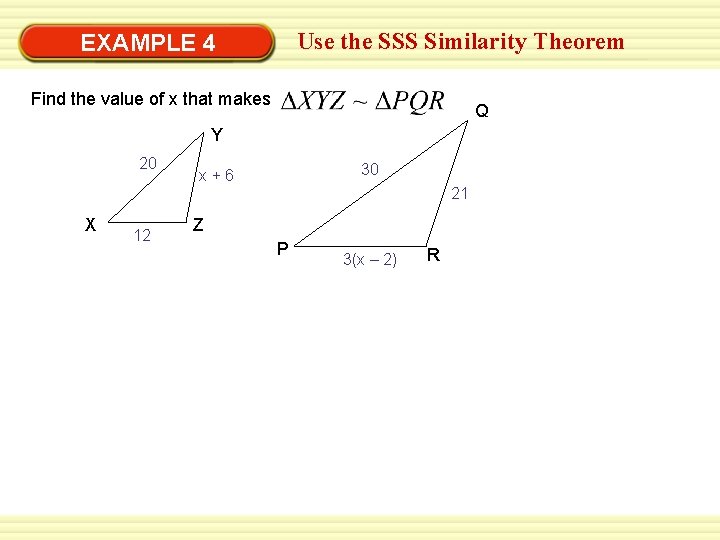
Use the SSS Similarity Theorem EXAMPLE 4 Find the value of x that makes Q Y 20 30 x+6 21 X 12 Z P 3(x – 2) R

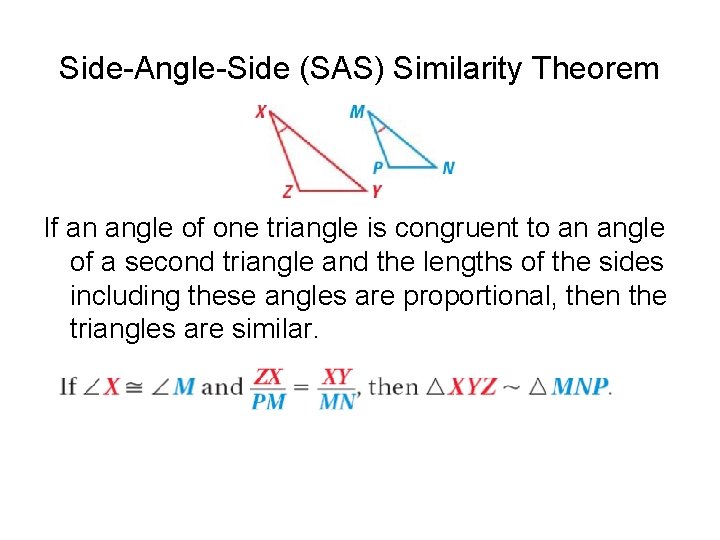
Side-Angle-Side (SAS) Similarity Theorem If an angle of one triangle is congruent to an angle of a second triangle and the lengths of the sides including these angles are proportional, then the triangles are similar.

EXAMPLE 5 Use the SAS Similarity Theorem Lean-to Shelter You are building a lean-to shelter starting from a tree branch, as shown. Can you construct the right end so it is similar to the left end using the angle measure and lengths shown?

EXAMPLE 5 Use the SAS Similarity Theorem (continued) SOLUTION Both m A and m F equal = 53°, so A ~ F. Next, compare the ratios of the lengths of the sides that include A and F. Shorter sides Longer sides AB 9 3 AC 15 3 = = FG 6 2 FH = 10 = 2 The lengths of the sides that include A and proportional. F are ANSWER So, by the SAS Similarity Theorem, ABC ~ FGH. Yes, you can make the right end similar to the left end of the shelter.

EXAMPLE 6 Choose a method Tell what method you would use to show that the triangles are similar. SOLUTION Find the ratios of the lengths of the corresponding sides. Shorter sides Longer sides BC 9 CA 18 3 3 EC = 15 = 5 CD = 30 = 5 The corresponding side lengths are proportional. The included angles ACB and DCE are congruent because they are vertical angles. So, ACB ~ DCE by the SAS Similarity Theorem.

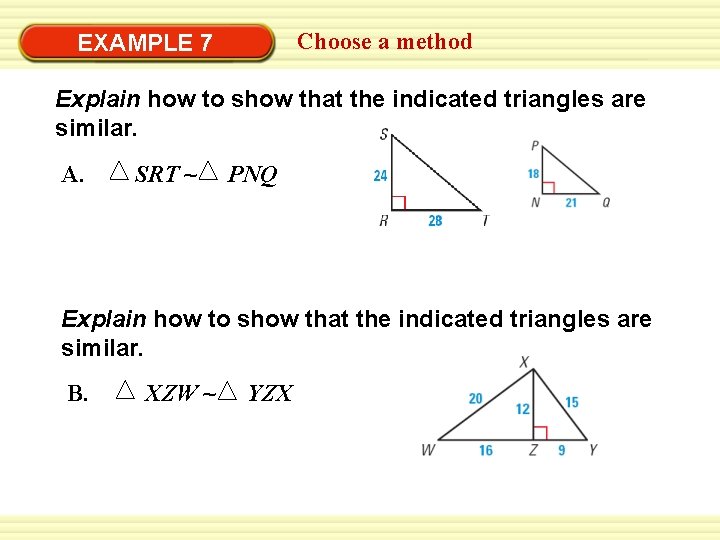
Choose a method EXAMPLE 7 Explain how to show that the indicated triangles are similar. A. SRT ~ PNQ Explain how to show that the indicated triangles are similar. B. XZW ~ YZX