Geometry Lesson 7 3 Similar Triangles Objective Identify

Geometry Lesson 7 – 3 Similar Triangles Objective: Identify similar triangles using the AA Similarity postulate and the SSS and SAS Similarity Theorem. Use similar triangles to solve problems.

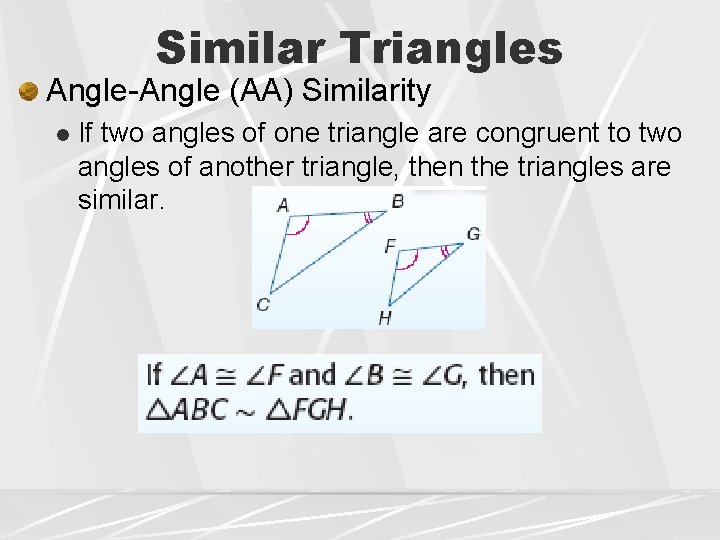
Similar Triangles Angle-Angle (AA) Similarity l If two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar.

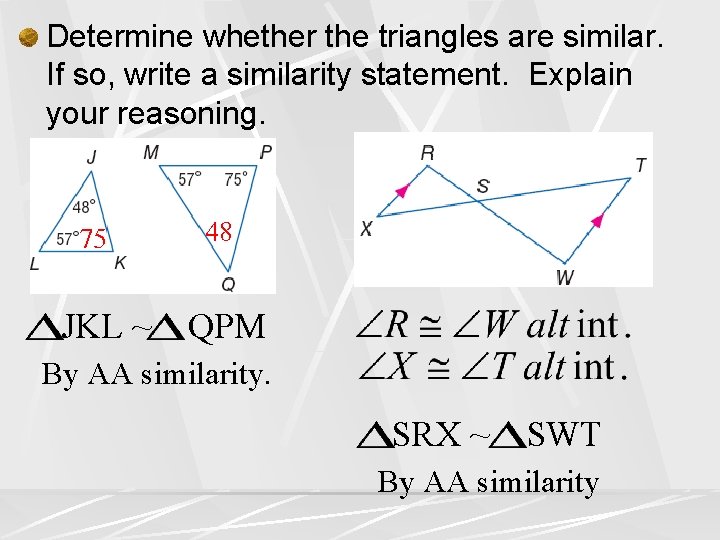
Determine whether the triangles are similar. If so, write a similarity statement. Explain your reasoning. 75 JKL ~ 48 QPM By AA similarity. SRX ~ SWT By AA similarity

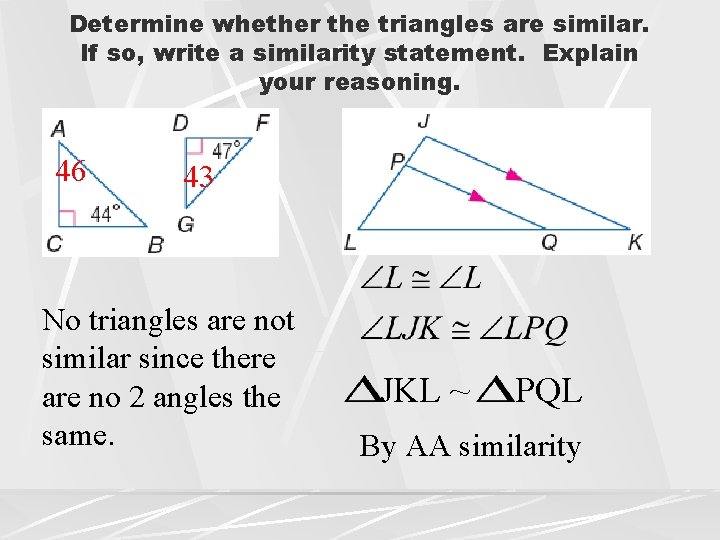
Determine whether the triangles are similar. If so, write a similarity statement. Explain your reasoning. 46 43 No triangles are not similar since there are no 2 angles the same. JKL ~ PQL By AA similarity

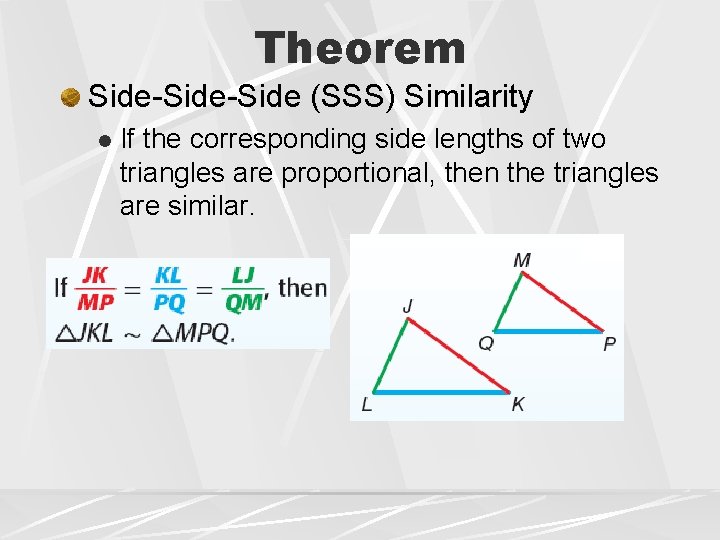
Theorem Side-Side (SSS) Similarity l If the corresponding side lengths of two triangles are proportional, then the triangles are similar.

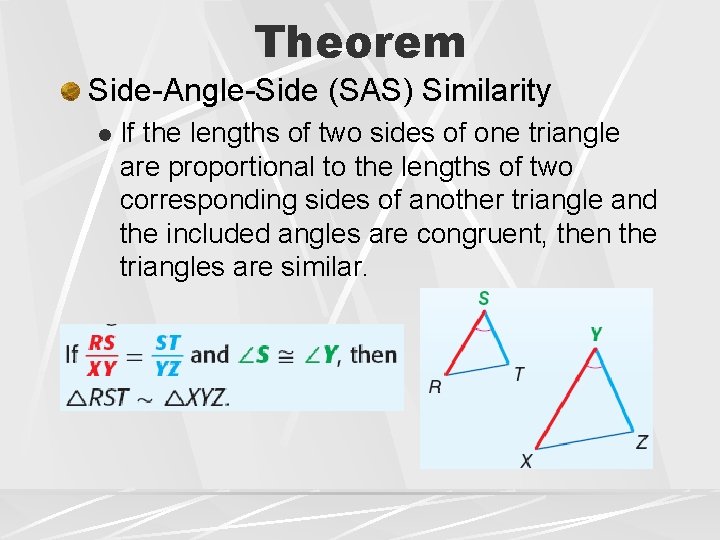
Theorem Side-Angle-Side (SAS) Similarity l If the lengths of two sides of one triangle are proportional to the lengths of two corresponding sides of another triangle and the included angles are congruent, then the triangles are similar.

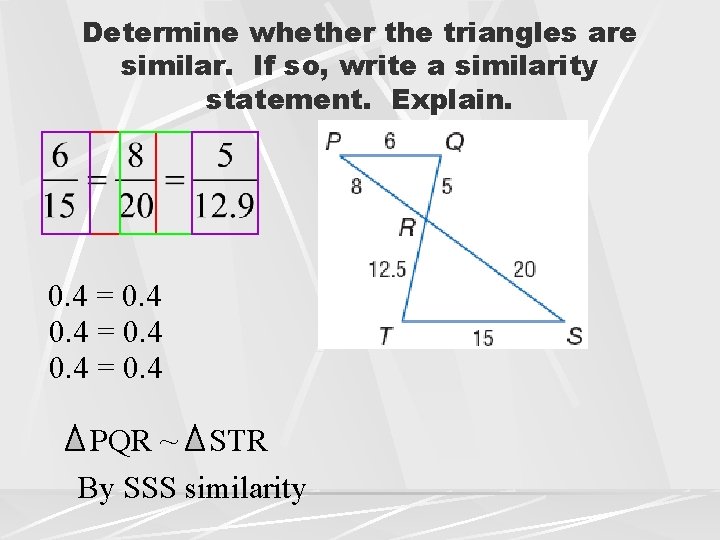
Determine whether the triangles are similar. If so, write a similarity statement. Explain. 0. 4 = 0. 4 PQR ~ STR By SSS similarity

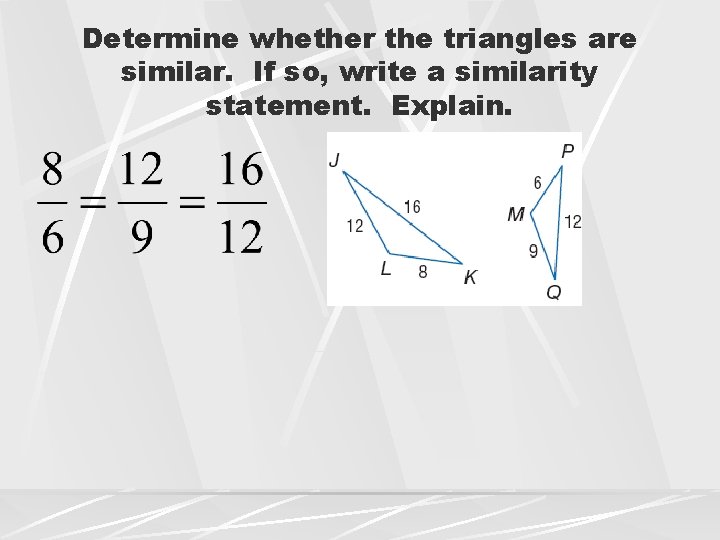
Determine whether the triangles are similar. If so, write a similarity statement. Explain.

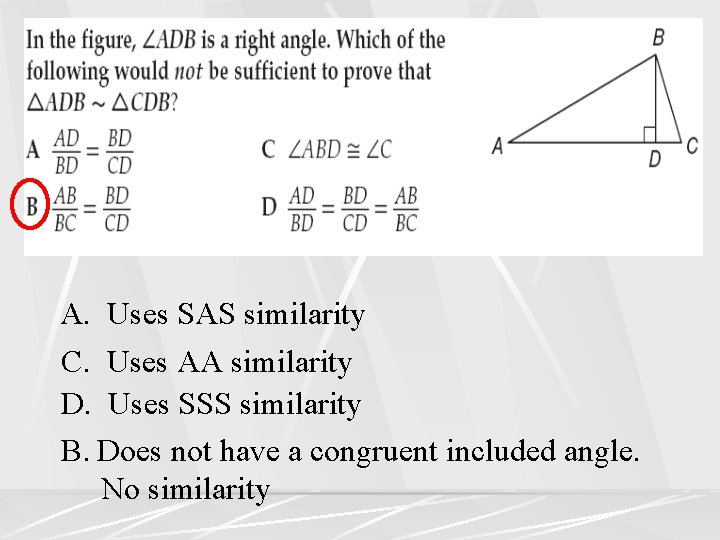
A. Uses SAS similarity C. Uses AA similarity D. Uses SSS similarity B. Does not have a congruent included angle. No similarity

B is the only choice that satisfies a similarity condition. SSS similarity.

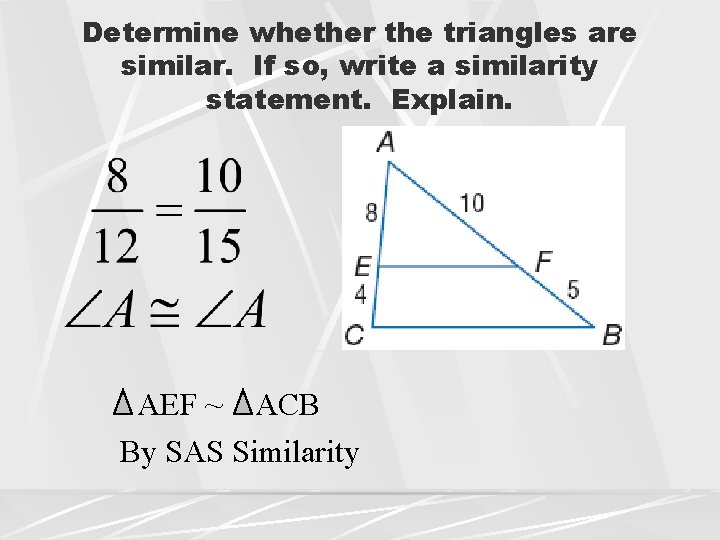
Determine whether the triangles are similar. If so, write a similarity statement. Explain. AEF ~ ACB By SAS Similarity

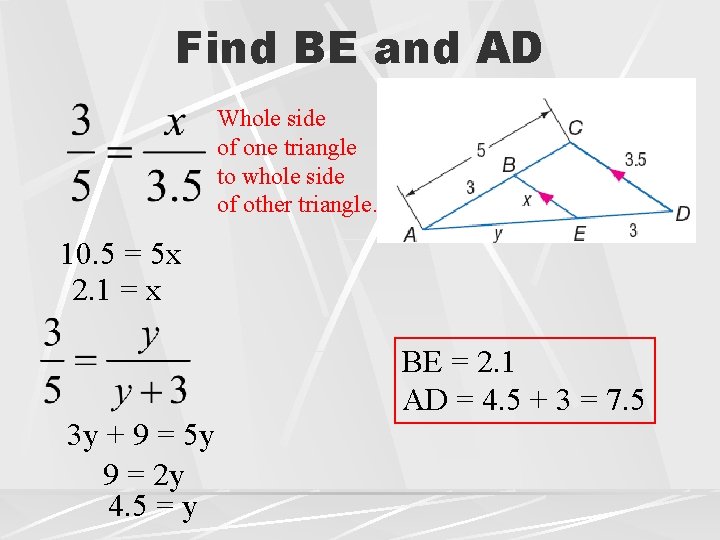
Find BE and AD Whole side of one triangle to whole side of other triangle. 10. 5 = 5 x 2. 1 = x 3 y + 9 = 5 y 9 = 2 y 4. 5 = y BE = 2. 1 AD = 4. 5 + 3 = 7. 5

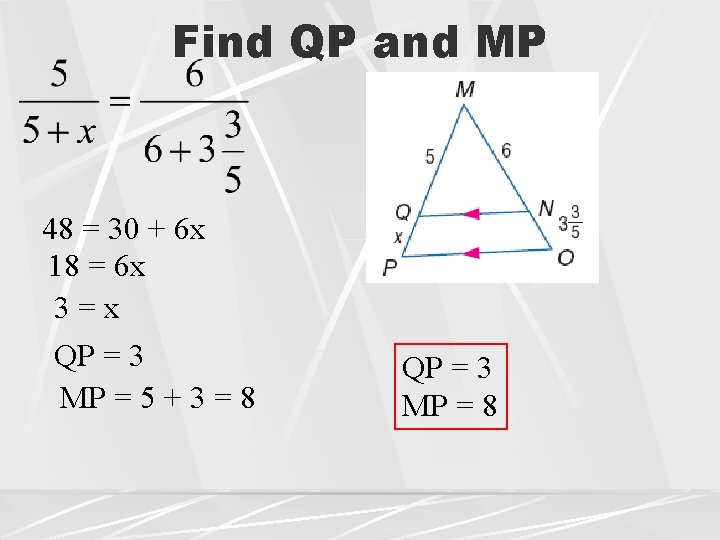
Find QP and MP 48 = 30 + 6 x 18 = 6 x 3=x QP = 3 MP = 5 + 3 = 8 QP = 3 MP = 8

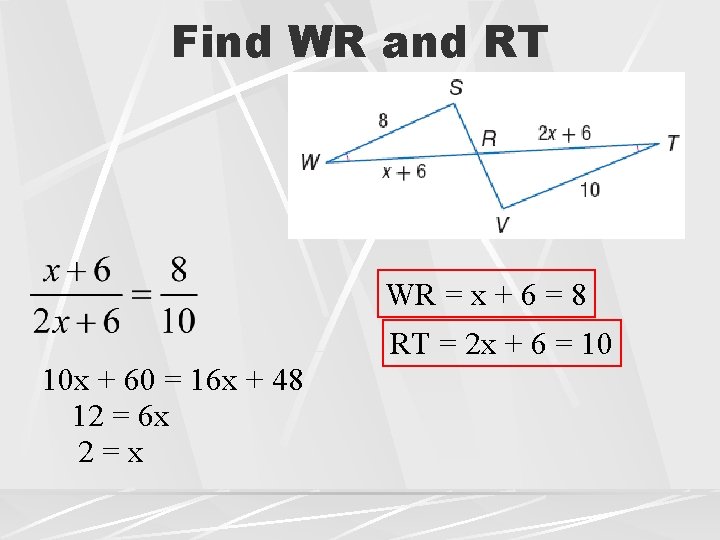
Find WR and RT WR = x + 6 = 8 RT = 2 x + 6 = 10 10 x + 60 = 16 x + 48 12 = 6 x 2=x

Real world Adam is standing next to the Palmetto Building in Columbia, South Carolina. He is 6 feet tall and the length of his shadow is 9 feet. If the length of the shadow of the building is 322. 5 feet, how tall is the building? The Palmetto building is 215 feet tall. 9 x = 1935 x = 215

Homework Pg. 479 1 – 8 all, 10 – 24 E, 38, 42 – 56 E