Unit 11 Advanced Triangles This unit finishes the























- Slides: 43

Unit 11 Advanced Triangles • This unit finishes the analysis of triangles with Triangle Similarity (AA, SAS, SSS). • This unit also addressed Geometric Means, and triangle bisectors, and the side-splitter theorem. • This unit also contains the complete set of instructions addressing Right Triangle Trigonometry (SOHCAHTOA). (Different set of slides)

Standards • • • SPI’s taught in Unit 9: SPI 3108. 1. 1 Give precise mathematical descriptions or definitions of geometric shapes in the plane and space. SPI 3108. 4. 7 Compute the area and/or perimeter of triangles, quadrilaterals and other polygons when one or more additional steps are required (e. g. find missing dimensions given area or perimeter of the figure, using trigonometry). SPI 3108. 4. 9 Use right triangle trigonometry and cross-sections to solve problems involving surface areas and/or volumes of solids. SPI 3108. 4. 15 Determine and use the appropriate trigonometric ratio for a right triangle to solve a contextual problem. CLE (Course Level Expectations) found in Unit 9: CLE 3108. 1. 4 Move flexibly between multiple representations (contextual, physical written, verbal, iconic/pictorial, graphical, tabular, and symbolic), to solve problems, to model mathematical ideas, and to communicate solution strategies. CLE 3108. 1. 5 Recognize and use mathematical ideas and processes that arise in different settings, with an emphasis on formulating a problem in mathematical terms, interpreting the solutions, mathematical ideas, and communication of solution strategies. CLE 3108. 1. 7 Use technologies appropriately to develop understanding of abstract mathematical ideas, to facilitate problem solving, and to produce accurate and reliable models. CLE 3108. 2. 3 Establish an ability to estimate, select appropriate units, evaluate accuracy of calculations and approximate error in measurement in geometric settings. CLE 3108. 4. 8 Establish processes for determining congruence and similarity of figures, especially as related to scale factor, contextual applications, and transformations. CLE 3108. 4. 10 Develop the tools of right triangle trigonometry in the contextual applications, including the Pythagorean Theorem, Law of Sines and Law of Cosines

Standards • • • CFU (Checks for Understanding) applied to Unit 9: 3108. 1. 5 Use technology, hands-on activities, and manipulatives to develop the language and the concepts of geometry, including specialized vocabulary (e. g. graphing calculators, interactive geometry software such as Geometer’s Sketchpad and Cabri, algebra tiles, pattern blocks, tessellation tiles, MIRAs, mirrors, spinners, geoboards, conic section models, volume demonstration kits, Polyhedrons, measurement tools, compasses, Penta. Blocks, pentominoes, cubes, tangrams). 3108. 1. 7 Recognize the capabilities and the limitations of calculators and computers in solving problems. . . 3108. 1. 8 Understand how the similarity of right triangles allows the trigonometric functions sine, cosine, and tangent to be defined as ratio of sides. 3108. 4. 11 Use the triangle inequality theorems (e. g. , Exterior Angle Inequality Theorem, Hinge Theorem, SSS Inequality Theorem, Triangle Inequality Theorem) to solve problems. 3108. 4. 27 Use right triangle trigonometry to find the area and perimeter of quadrilaterals (e. g. square, rectangle, rhombus, parallelogram, trapezoid, and kite). 3108. 4. 36 Use several methods, including AA, SSS, and SAS, to prove that two triangles are similar. 3108. 4. 37 Identify similar figures and use ratios and proportions to solve mathematical and real-world problems (e. g. , Golden Ratio). 3108. 4. 42 Use geometric mean to solve problems involving relationships that exist when the altitude is drawn to the hypotenuse of a right triangle. 3108. 4. 47 Find the sine, cosine and tangent ratios of an acute angle of a right triangle given the side lengths. 3108. 4. 48 Define, illustrate, and apply angles of elevation and angles of depression in real-world situations. 3108. 4. 49 Use the Law of Sines (excluding the ambiguous case) and the Law of Cosines to find missing side lengths and/or angle measures in non-right triangles.

Introduction • Previously, we learned how to prove triangles congruent • Now we will look at how to prove triangles are similar • As a reminder, by definition triangles are similar if they have congruent angles, and sides which have a uniform similarity ratio

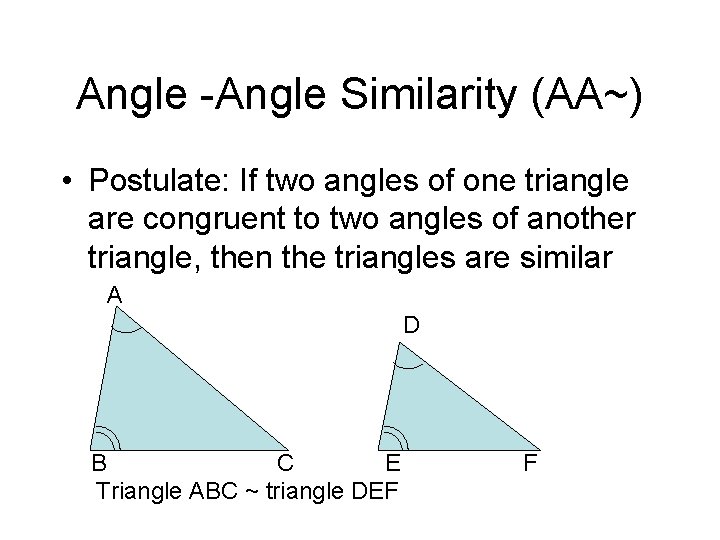
Angle -Angle Similarity (AA~) • Postulate: If two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar A D B C E Triangle ABC ~ triangle DEF F

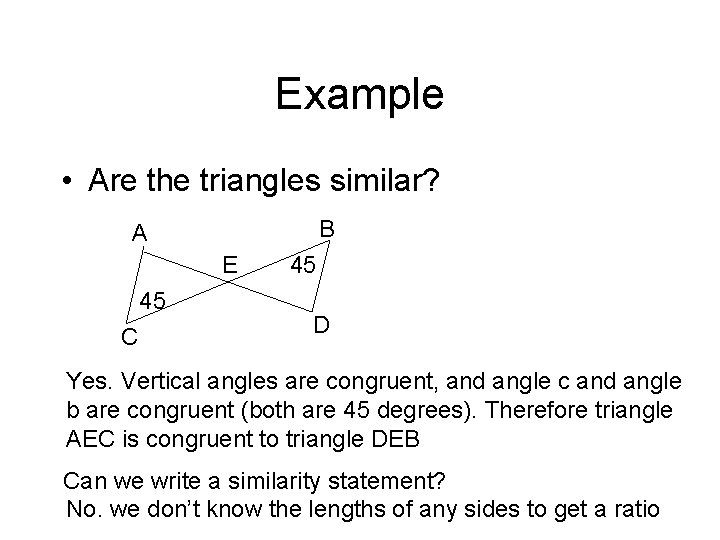
Example • Are the triangles similar? B A E 45 C 45 D Yes. Vertical angles are congruent, and angle c and angle b are congruent (both are 45 degrees). Therefore triangle AEC is congruent to triangle DEB Can we write a similarity statement? No. we don’t know the lengths of any sides to get a ratio

Side Angle Side Similarity (SAS ~) • If an angle of one triangle is congruent to an angle of a second triangle, and the sides which are connected to each angle are proportional, then the triangles are similar • This makes sense if you look at it. The “pivot” angle dictates the opposite side, and if the two sides are in ratio, then the opposite side would be as well

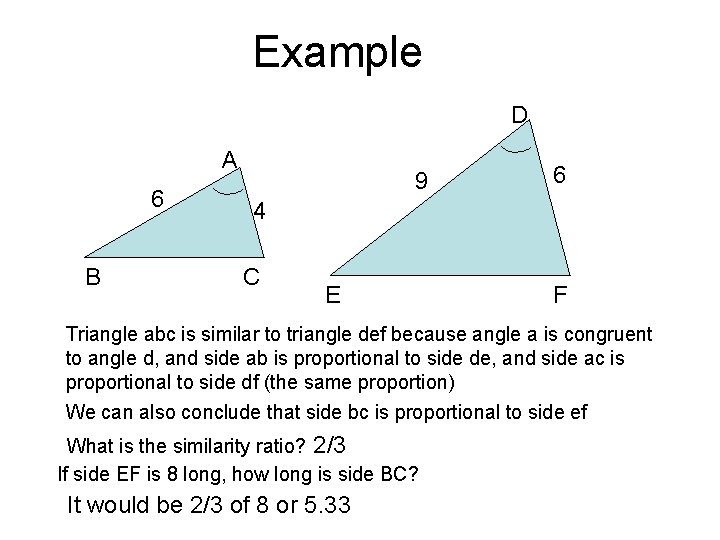
Example D A 6 B 9 6 4 C E F Triangle abc is similar to triangle def because angle a is congruent to angle d, and side ab is proportional to side de, and side ac is proportional to side df (the same proportion) We can also conclude that side bc is proportional to side ef What is the similarity ratio? 2/3 If side EF is 8 long, how long is side BC? It would be 2/3 of 8 or 5. 33

Side-Side Similarity (SSS ~) • If the corresponding sides of two triangles are proportional, then the triangles are similar • Again, this makes sense. If all sides are in proportion, then the angles will necessarily be equal, which is the definition of similar • No matter how you try to put the second triangle together, it will only fit one way, and that way will produce a similar triangle

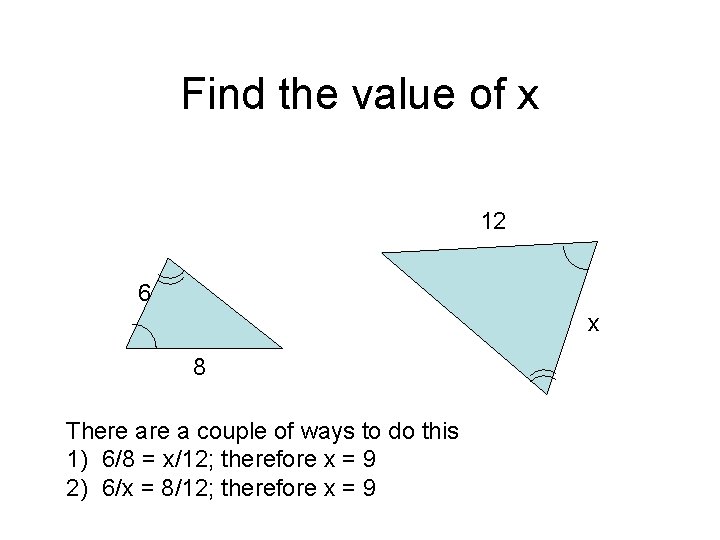
Find the value of x 12 6 x 8 There a couple of ways to do this 1) 6/8 = x/12; therefore x = 9 2) 6/x = 8/12; therefore x = 9

Assignment • Page 455 7 -12 • Page 457 24 -26

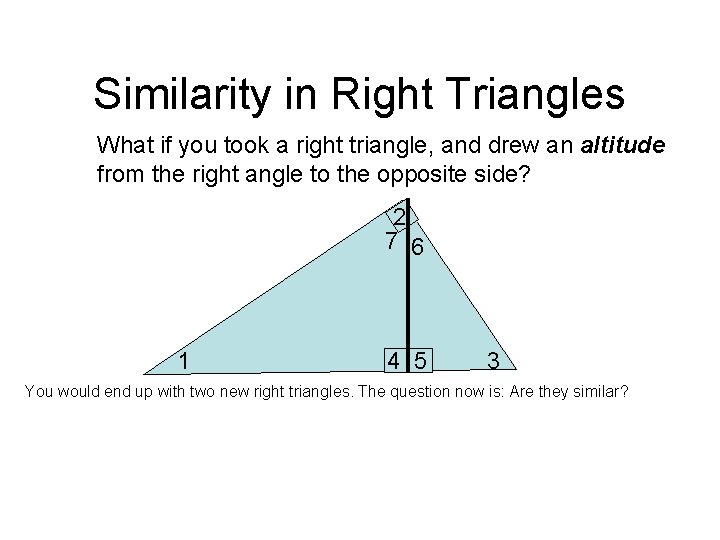
Similarity in Right Triangles What if you took a right triangle, and drew an altitude from the right angle to the opposite side? 2 7 6 1 4 5 3 You would end up with two new right triangles. The question now is: Are they similar?

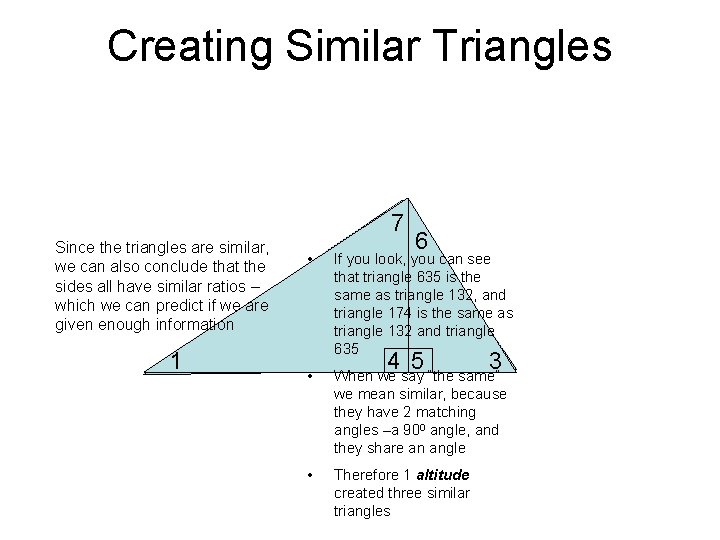
Creating Similar Triangles 72 Since the triangles are similar, we can also conclude that the sides all have similar ratios – which we can predict if we are given enough information 1 6 • If you look, you can see that triangle 635 is the same as triangle 132, and triangle 174 is the same as triangle 132 and triangle 635 • When we say “the same” we mean similar, because they have 2 matching angles –a 900 angle, and they share an angle • Therefore 1 altitude created three similar triangles 4 5 3

Right Triangles and Altitudes • The altitude to the hypotenuse of a right triangle divides the triangle into two triangles that are similar to the original triangle, and to each other • A point to keep in mind: if you know the measure of the original angles of the first triangle, by default you will know the measure of all the angles of all 3 triangles

Finding the Geometric Mean • KNOW THIS • Proportions in which means (averages) are equal occur frequently in geometry • For any 2 positive numbers -such as a and b, • the geometric mean of a and b is the positive number x such that a/x = x/b Therefore: x = √ab

An example of Geometric Mean • • Find the geometric mean of 4 and 18 Write the proportion: 4/x = x/18 Cross multiply X*X = 4*18 or X 2 = 72 X = √ 72 It should be noted, that this is in fact X = √a*b or X = √ 4*18, so if I can remember how this works, I can jump to this step • So, X = 6 √ 2 • Yep, more radicals….

Another Example of Geometric Mean • Find the geometric mean of 3 and 12 We can do it the long way 3/X = X/12 Or cut to the final step where X= √ 12*3 Therefore, x = 6

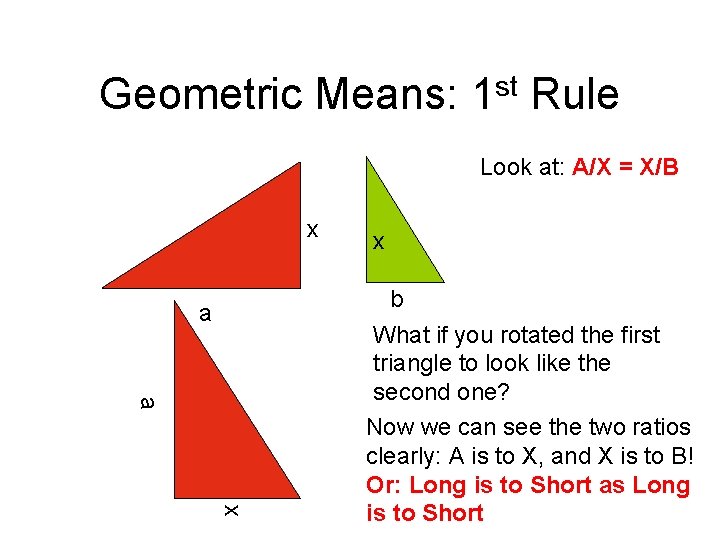
Geometric Means and Altitudes: 1 st Rule • The length of the altitude to the hypotenuse (same altitude as before) of a right triangle is the geometric mean of the lengths of the segments of the hypotenuse. • AD/CD = CD/DB • If you look at the two triangles, this is the ratio of the long side to the short side of triangle c ACD = the ratio of the long side to the short side of triangle CBD a d b

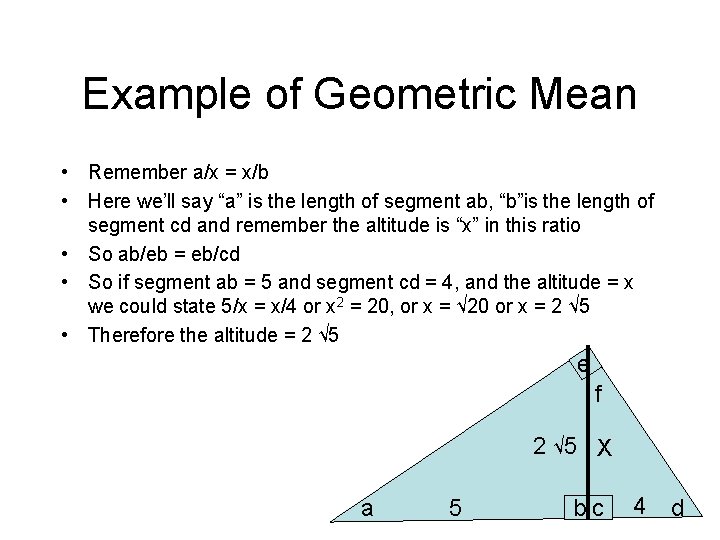
Example of Geometric Mean • Remember a/x = x/b • Here we’ll say “a” is the length of segment ab, “b”is the length of segment cd and remember the altitude is “x” in this ratio • So ab/eb = eb/cd • So if segment ab = 5 and segment cd = 4, and the altitude = x we could state 5/x = x/4 or x 2 = 20, or x = √ 20 or x = 2 √ 5 • Therefore the altitude = 2 √ 5 e f 2 √ 5 X a 5 bc 4 d

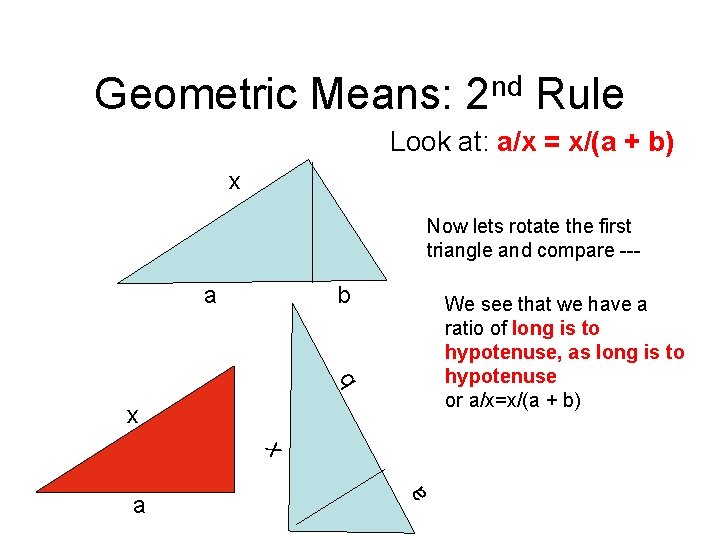
Hypotenuse and Geometric Means: 2 nd and 3 rd Rule • The altitude to the hypotenuse of a right triangle separates the hypotenuse so that the length of each leg of the triangle is the geometric mean of the length of the adjacent hypotenuse segment and the length of the hypotenuse. c • AD/AC = AC/AB • DB/CB = CB/AB a d b

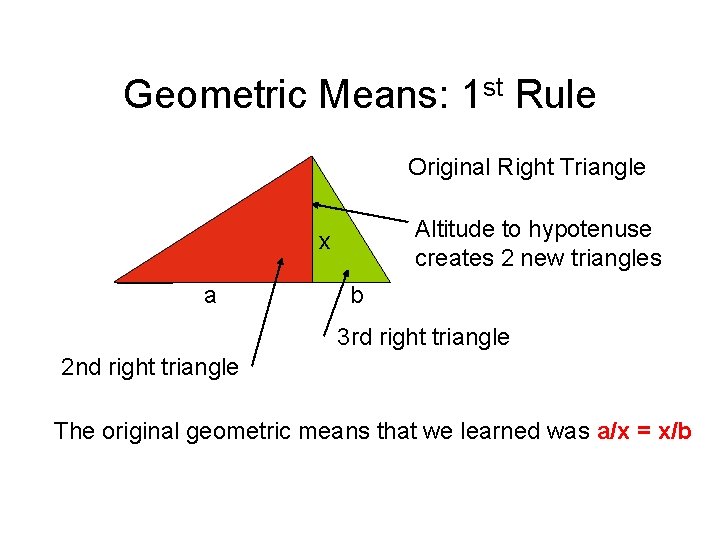
Geometric Means: 1 st Rule Original Right Triangle Altitude to hypotenuse creates 2 new triangles x a b 3 rd right triangle 2 nd right triangle The original geometric means that we learned was a/x = x/b

Geometric Means: 1 st Rule Look at: A/X = X/B x a x b What if you rotated the first triangle to look like the second one? Now we can see the two ratios clearly: A is to X, and X is to B! Or: Long is to Short as Long is to Short

Geometric Means: 2 nd Rule Look at: a/x = x/(a + b) x Now lets rotate the first triangle and compare --- b We see that we have a ratio of long is to hypotenuse, as long is to hypotenuse or a/x=x/(a + b) b a a a x x

Geometric Means: 3 rd Rule Look at: b/x x a Here, “short side to hypotenuse”, is x to (a+b), or x/(a+b) So: short side to hypotenuse is to short side is to hypotenuse is the same as: b/x = x/(a+b)! b b Again, we set up the ratio b/x, which is short side”to hypotenuse Let’s rotate the first triangle a x b = x/(a+b) x

Conclusions • 1 st, remember we are comparing similar triangles • Previously, we had 3 out of 4 numbers, we would create a ratio, and solve for x • Now we have 2 out of four numbers, but we can use geometric means, and still solve for x, as long as we can find the proper relationship • Also, it seems clear that we often need the length of the hypotenuse. We can find this by using the Pythagorean theorem, or a 2+b 2=c 2

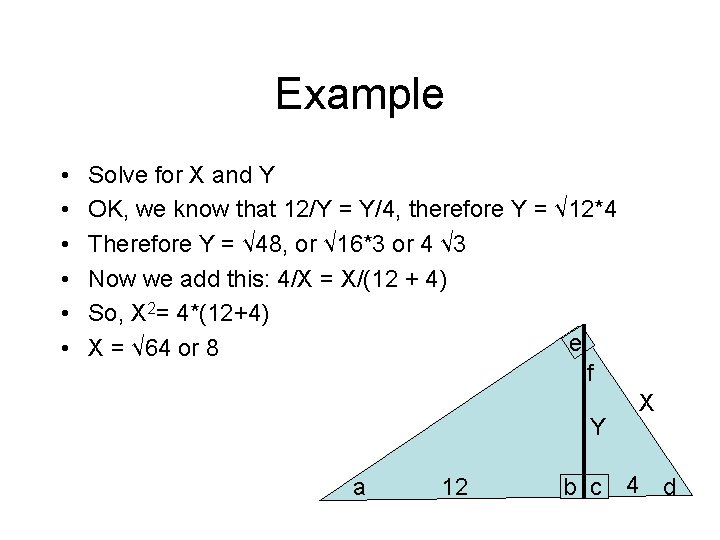
Example • • • Solve for X and Y OK, we know that 12/Y = Y/4, therefore Y = √ 12*4 Therefore Y = √ 48, or √ 16*3 or 4 √ 3 Now we add this: 4/X = X/(12 + 4) So, X 2= 4*(12+4) e X = √ 64 or 8 f Y a 12 b c X 4 d

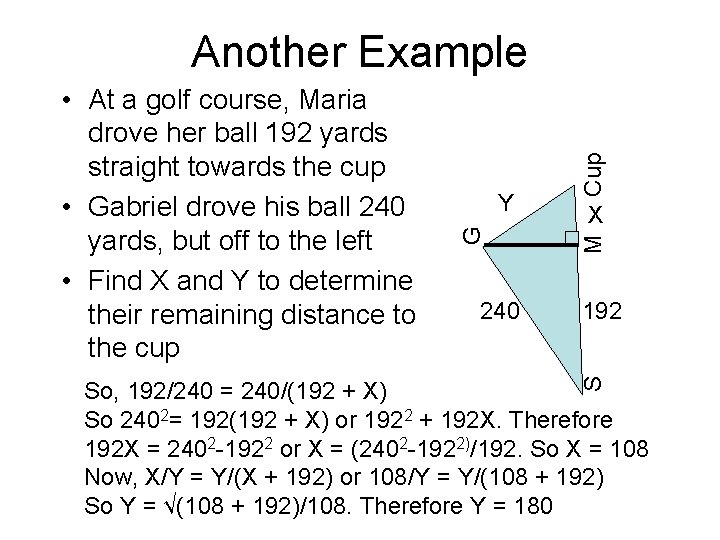
240 M X 192 S Y G • At a golf course, Maria drove her ball 192 yards straight towards the cup • Gabriel drove his ball 240 yards, but off to the left • Find X and Y to determine their remaining distance to the cup Cup Another Example So, 192/240 = 240/(192 + X) So 2402= 192(192 + X) or 1922 + 192 X. Therefore 192 X = 2402 -1922 or X = (2402 -1922)/192. So X = 108 Now, X/Y = Y/(X + 192) or 108/Y = Y/(108 + 192) So Y = √(108 + 192)/108. Therefore Y = 180

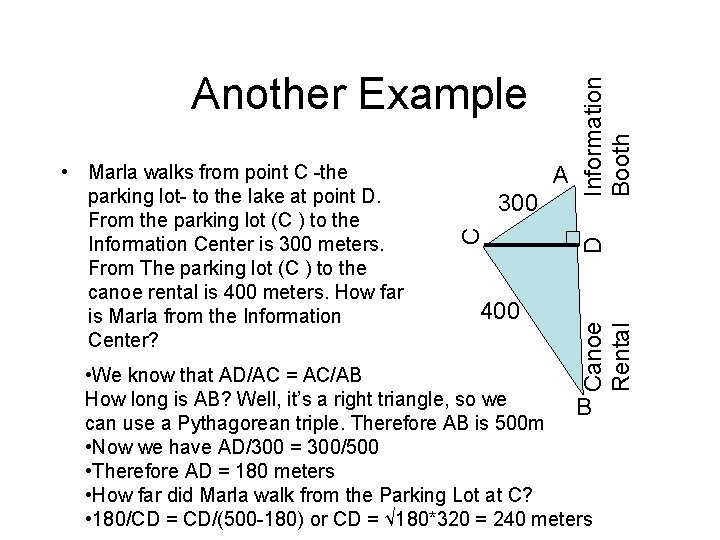
400 Information Booth 300 D A C • Marla walks from point C -the parking lot- to the lake at point D. From the parking lot (C ) to the Information Center is 300 meters. From The parking lot (C ) to the canoe rental is 400 meters. How far is Marla from the Information Center? Canoe Rental Another Example • We know that AD/AC = AC/AB How long is AB? Well, it’s a right triangle, so we B can use a Pythagorean triple. Therefore AB is 500 m • Now we have AD/300 = 300/500 • Therefore AD = 180 meters • How far did Marla walk from the Parking Lot at C? • 180/CD = CD/(500 -180) or CD = √ 180*320 = 240 meters

Assignment • Page 468 17 -22 • Geometric Means worksheet 1 and 2

Page 99 in workbook • On problems 1, 2, and 3 you can use the Py-theorem to solve for the hypotenuse, or the missing side • On problem 4 you can use the Pytheorem to solve for x and y, you don’t even need geometric means • Problem 5 and 6 are ratios, set up the way we just discussed

Page 99 continued • To solve problems 7 and 8 you need to draw a picture first: • You are asked to solve 24 10 x for x, but first you need to find a and b, so that a b you can get the ratio of 26 a/x = x/b • Problem 8 is the same with different numbers • Problem 9 wants to see this set up as well, just with letters instead of numbers

Page 100 • The first 6 problems are straight geometric means where x = √a·b • Just solve as a decimal, it doesn’t say to solve in reduced radical form • Problems 7 -12 are expecting you to look for those relationships between long side, short side, and hypotenuse between the 3 right triangles.

Page 100 continued • Problems 13 -22 expect you to find the relationships between the right triangles, and set up a solution • Some of them, such as #18, expect you to use the Py-theorem to find the length of a missing side before you solve for the variable

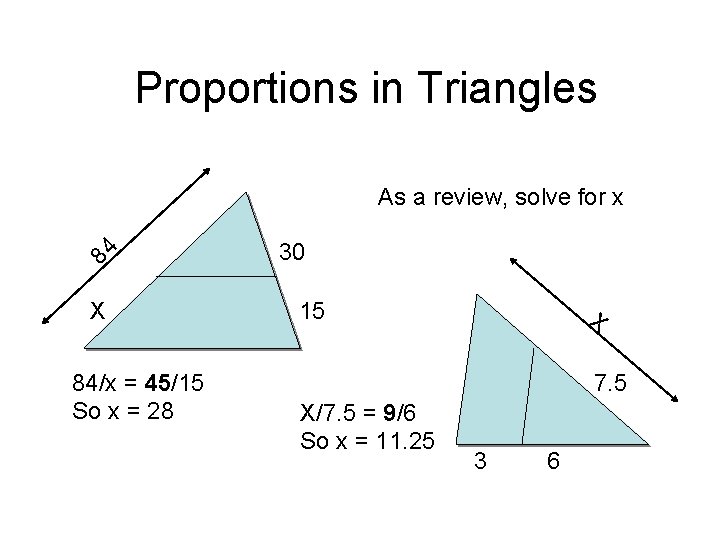
Proportions in Triangles 84 As a review, solve for x X 84/x = 45/15 So x = 28 30 15 X 7. 5 X/7. 5 = 9/6 So x = 11. 25 3 6

Side Splitter Theorem • If a line is parallel to one side of a triangle and intersects the other two sides, then it divides the sides proportionally

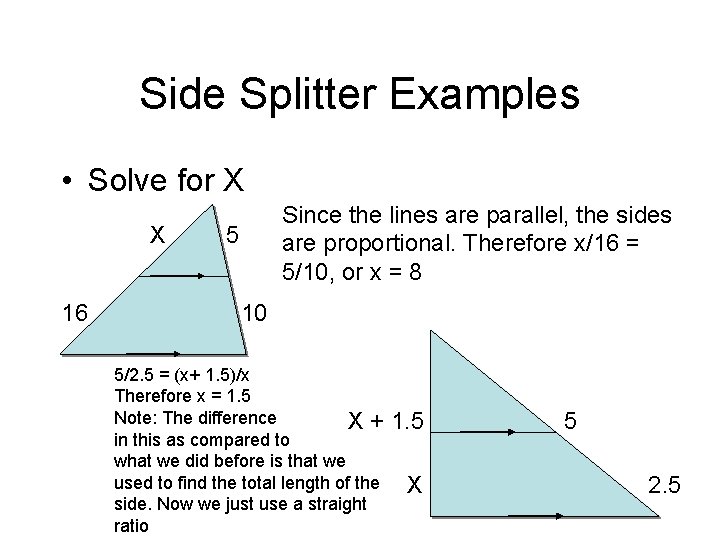
Side Splitter Examples • Solve for X X 16 Since the lines are parallel, the sides are proportional. Therefore x/16 = 5/10, or x = 8 5 10 5/2. 5 = (x+ 1. 5)/x Therefore x = 1. 5 Note: The difference X+ in this as compared to what we did before is that we used to find the total length of the side. Now we just use a straight ratio 1. 5 X 5 2. 5

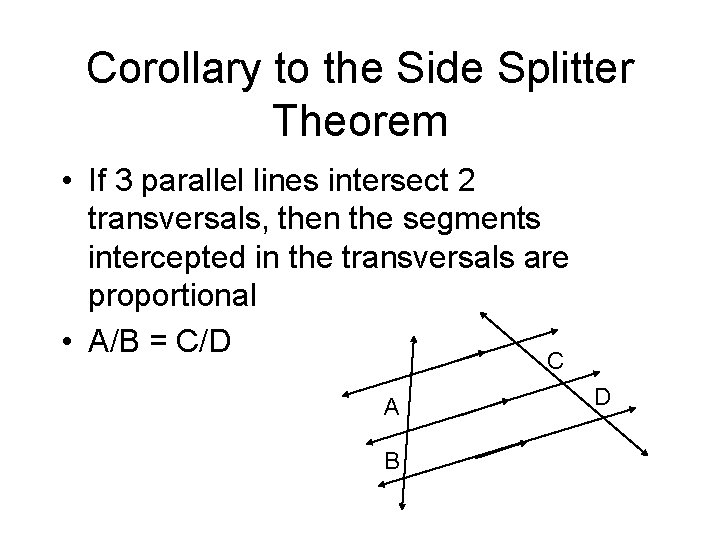
Corollary to the Side Splitter Theorem • If 3 parallel lines intersect 2 transversals, then the segments intercepted in the transversals are proportional • A/B = C/D C A B D

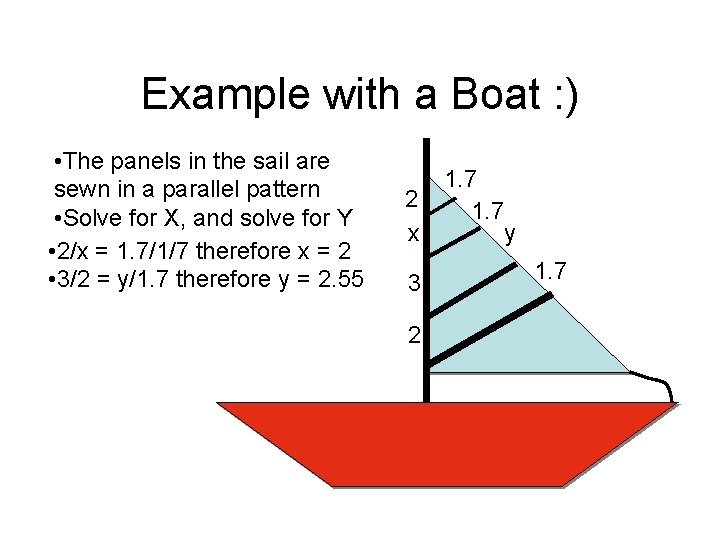
Example with a Boat : ) • The panels in the sail are sewn in a parallel pattern • Solve for X, and solve for Y • 2/x = 1. 7/1/7 therefore x = 2 • 3/2 = y/1. 7 therefore y = 2. 55 2 x 3 2 1. 7 y 1. 7

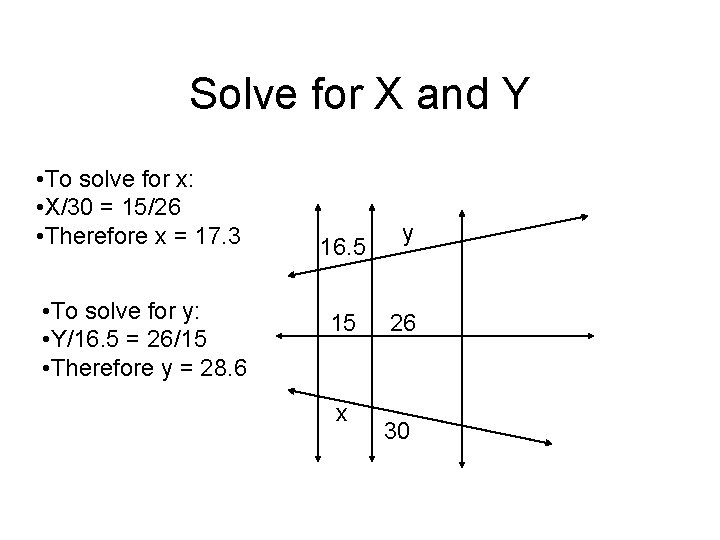
Solve for X and Y • To solve for x: • X/30 = 15/26 • Therefore x = 17. 3 • To solve for y: • Y/16. 5 = 26/15 • Therefore y = 28. 6 16. 5 15 x y 26 30

Triangle-Angle-Bisector Theorem • If a ray bisects an angle of a triangle, then it divides the opposite side into two segments that are proportional to the other two sides of the triangle

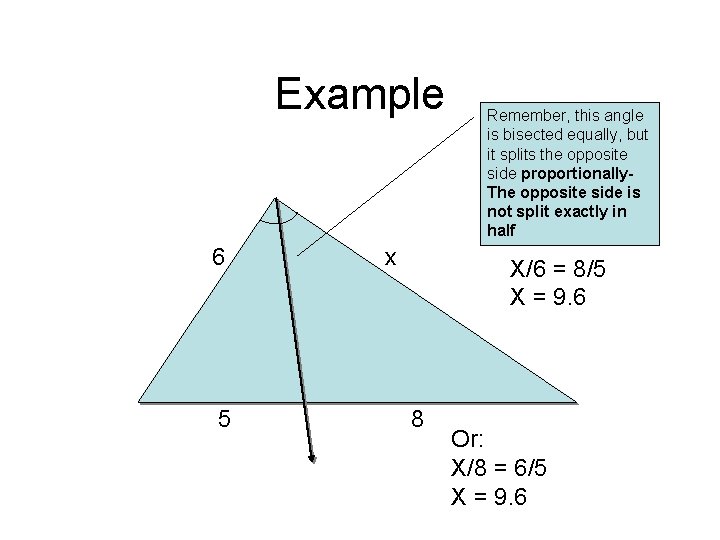
Example 6 5 x Remember, this angle is bisected equally, but it splits the opposite side proportionally. The opposite side is not split exactly in half X/6 = 8/5 X = 9. 6 8 Or: X/8 = 6/5 X = 9. 6

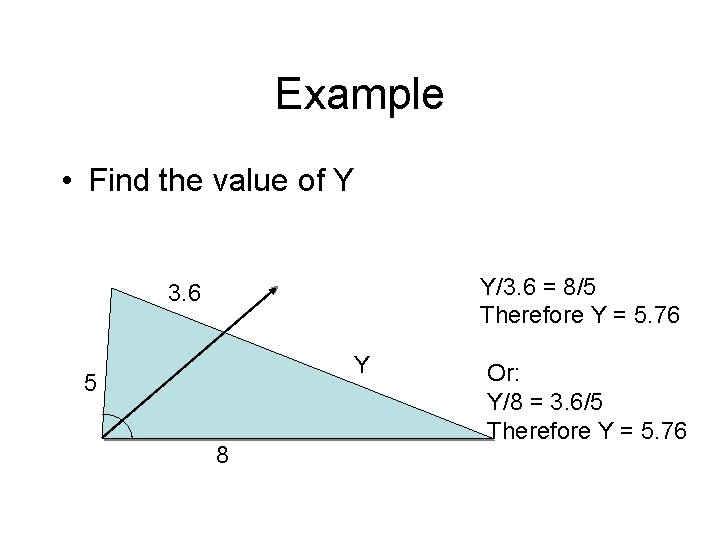
Example • Find the value of Y Y/3. 6 = 8/5 Therefore Y = 5. 76 3. 6 Y 5 8 Or: Y/8 = 3. 6/5 Therefore Y = 5. 76

Assignment • Page 475 9 -22 • Page 476 25 -35 • Worksheet 8 -5