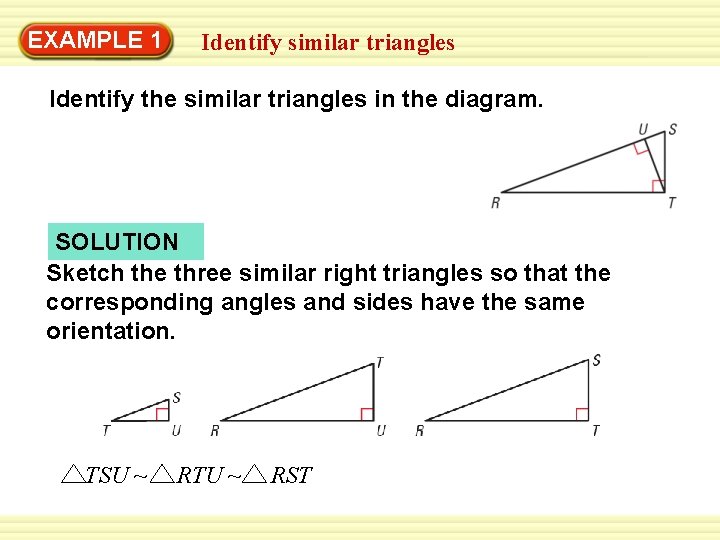
EXAMPLE 1 Identify similar triangles Identify the similar

EXAMPLE 1 Identify similar triangles Identify the similar triangles in the diagram. SOLUTION Sketch the three similar right triangles so that the corresponding angles and sides have the same orientation. TSU ~ RTU ~ RST

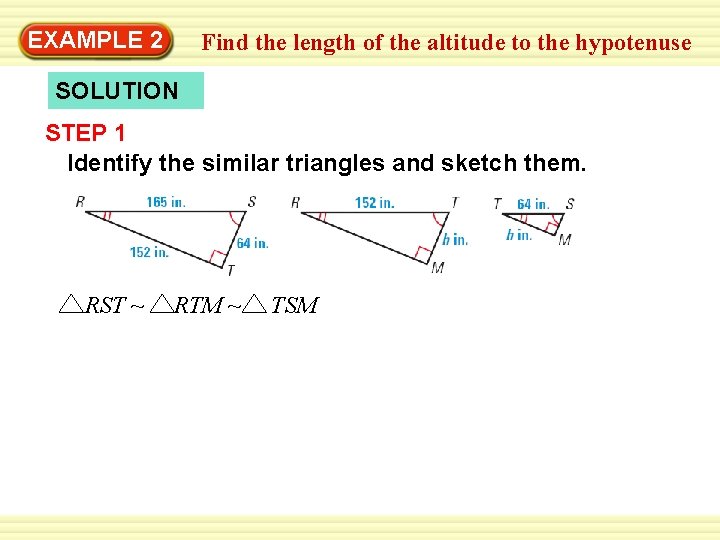
EXAMPLE 2 Find the length of the altitude to the hypotenuse Swimming Pool The diagram below shows a cross-section of a swimming pool. What is the maximum depth of the pool?

EXAMPLE 2 Find the length of the altitude to the hypotenuse SOLUTION STEP 1 Identify the similar triangles and sketch them. RST ~ RTM ~ TSM

EXAMPLE 2 Find the length of the altitude to the hypotenuse STEP 2 Find the value of h. Use the fact that RST ~ RTM to write a proportion. Corresponding side lengths of TM TR = similar triangles are in proportion. ST SR h 152 = Substitute. 64 165 Cross Products Property 165 h = 64(152) Solve for h. h 59 STEP 3 Read the diagram above. You can see that the maximum depth of the pool is h + 48, which is about 59 + 48 = 107 inches. The maximum depth of the pool is about 107 inches.

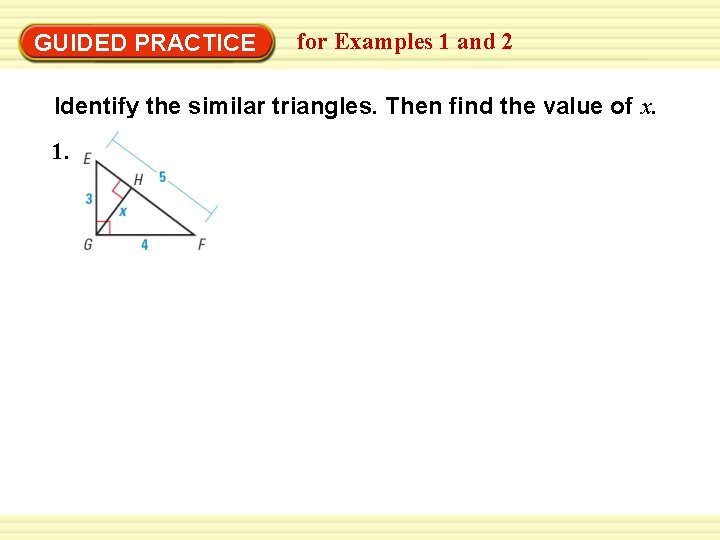
GUIDED PRACTICE for Examples 1 and 2 Identify the similar triangles. Then find the value of x. 1.

GUIDED PRACTICE for Examples 1 and 2 1. STEP 1 The similar triangle are GHF To find the value of x STEP 2 Use the fact that GH EG = GF EF 3 x = 5 4 5 x = 12 x= EGF ~ 12 5 EGF ~ EHG to write a population Corresponding side length of similar triangle are in proportion Substitute Cross products property Solve for x

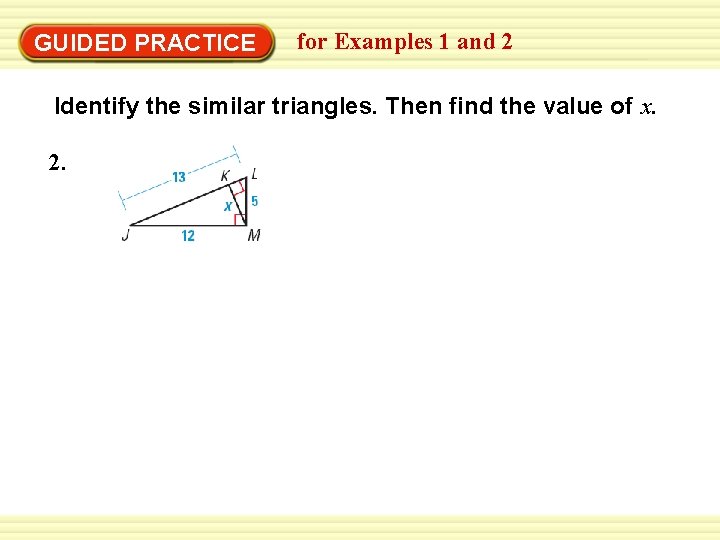
GUIDED PRACTICE for Examples 1 and 2 Identify the similar triangles. Then find the value of x. 2.

GUIDED PRACTICE for Examples 1 and 2 2. The similar triangle are LMJ ~ STEP 1 13 LKM L K x J MKJ ~ 12 5 M STEP 2 To find the value of x. use the fact that ~ MKJ to write a peroration LMJ

GUIDED PRACTICE KM ML = JM JL 5 x = 13 12 13 x = (12) (5) for Examples 1 and 2 Corresponding side length of similar triangle are in proportion Substitute Cross products property 13 x = 60 13 Solve for x