UNIT 6 Midsegments and Bisectors of Triangles Lets

UNIT 6 Midsegments and Bisectors of Triangles

Lets look at some formulas first. Slope: y 2 -y 1 x 2 -x 1 Midpoint: Distance:

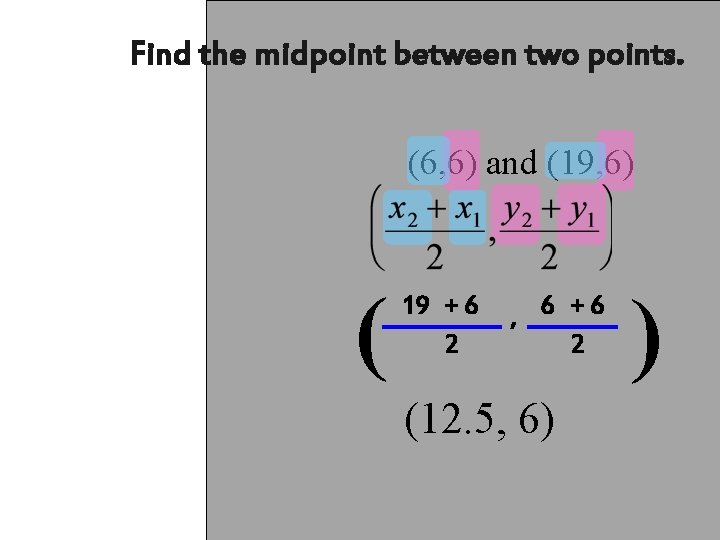
Find the midpoint between two points. (6, 6) and (19, 6) ( 19 + 6 2 , 6 +6 2 (12. 5, 6) )

Find the distince between two points. (6, 6) and (19, 6) 13

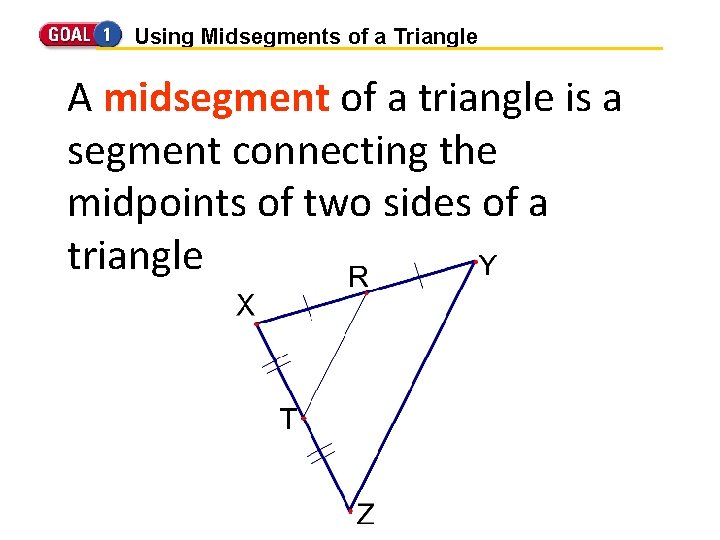
Using Midsegments of a Triangle A midsegment of a triangle is a segment connecting the midpoints of two sides of a triangle

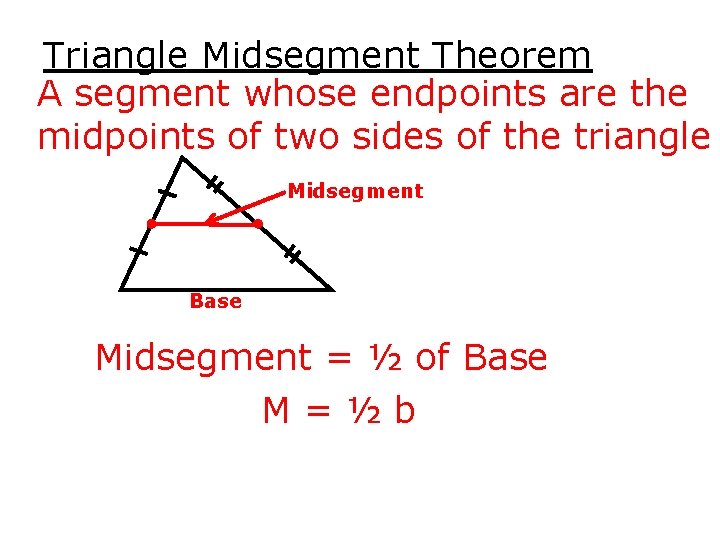
Triangle Midsegment Theorem A segment whose endpoints are the midpoints of two sides of the triangle Midsegment Base Midsegment = ½ of Base M=½b

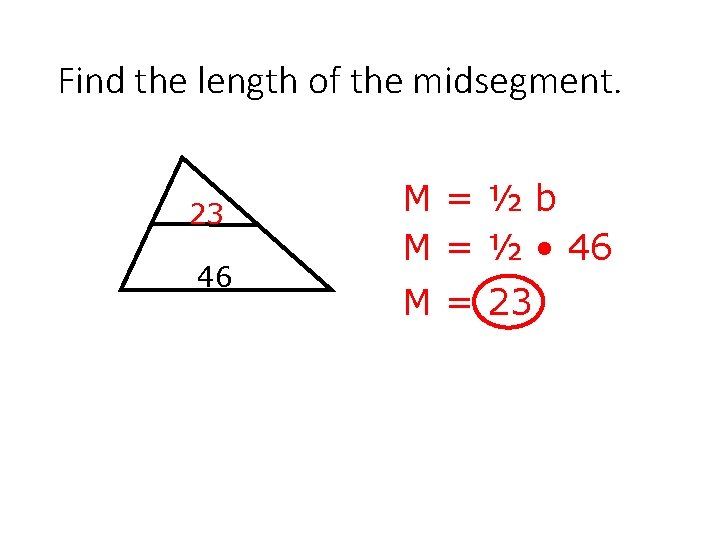
Find the length of the midsegment. 23 46 M=½b M = ½ • 46 M = 23

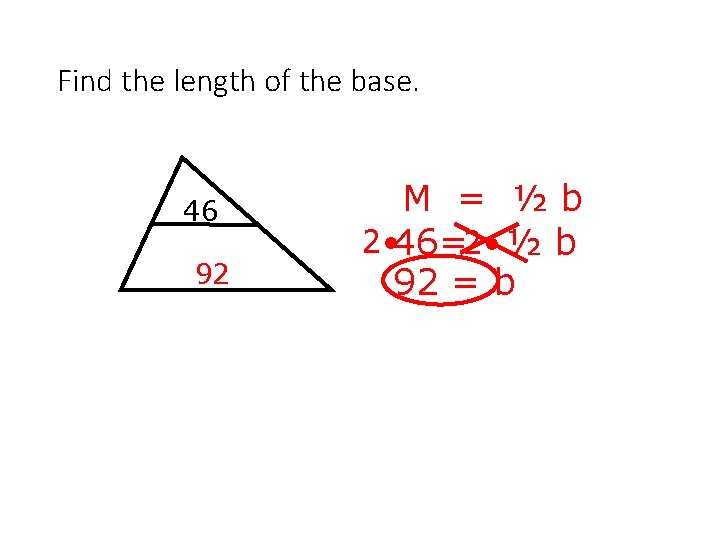
Find the length of the base. 46 92 M = ½b 2 • 46=2 • ½ b 92 = b

Find the length of the midsegment and the base. 5 • 3 -1 = 14 5 x - 1 6 x + 10 6 • 3+10 = 28 M = ½b 5 x - 1 = ½(6 x + 10) 5 x - 1 = 3 x + 5 -3 x 2 x - 1 = 5 +1 +1 2 x = 6 2 2 x=3

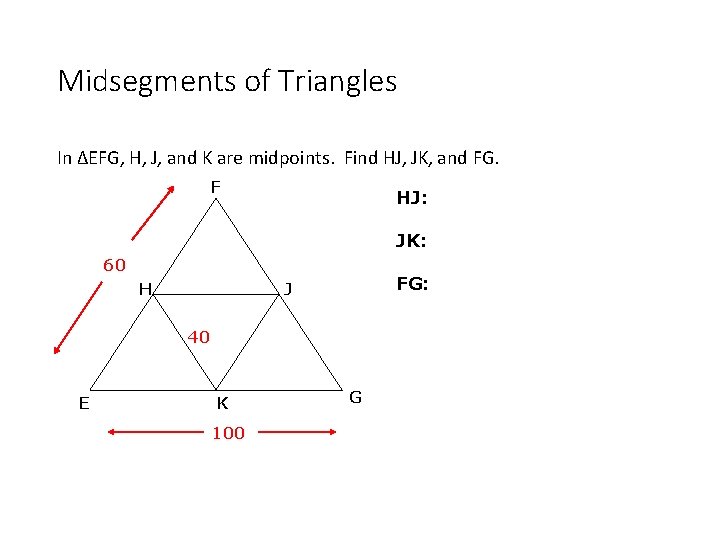
Midsegments of Triangles In ΔEFG, H, J, and K are midpoints. Find HJ, JK, and FG. F HJ: JK: 60 H FG: J 40 E K 100 G

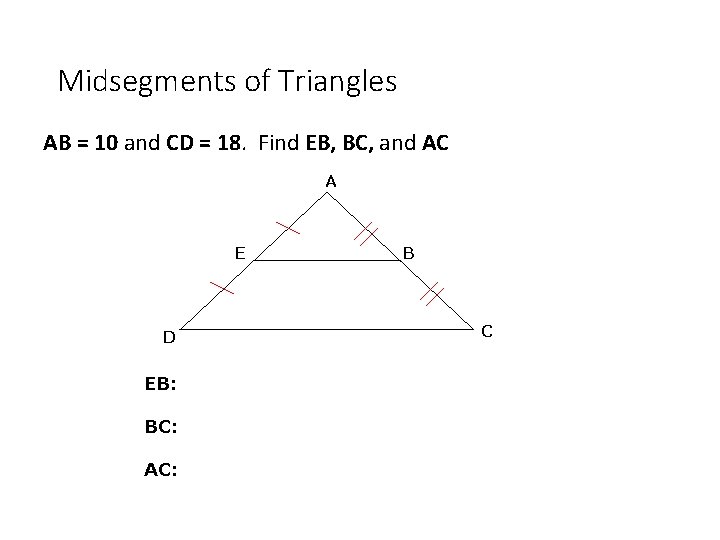
Midsegments of Triangles AB = 10 and CD = 18. Find EB, BC, and AC A E D EB: BC: AC: B C

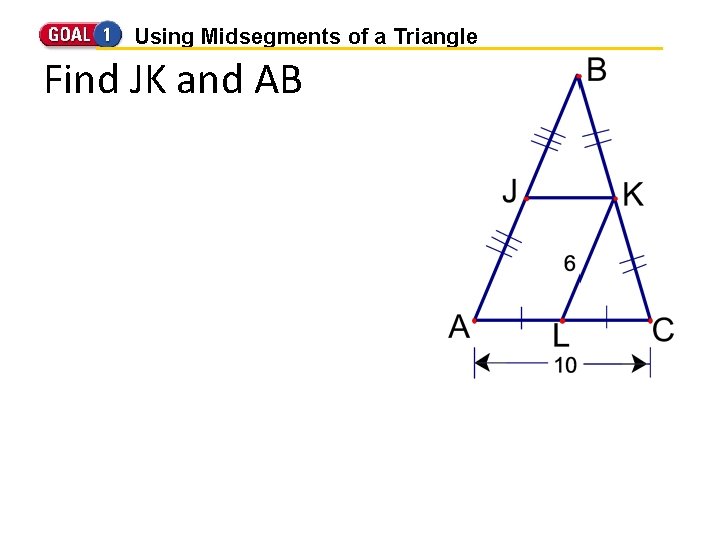
Using Midsegments of a Triangle Find JK and AB

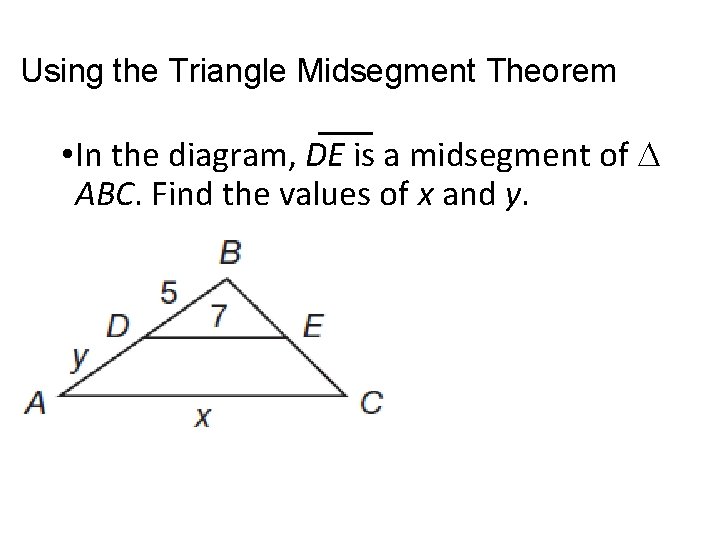
Using the Triangle Midsegment Theorem • In the diagram, DE is a midsegment of ABC. Find the values of x and y.

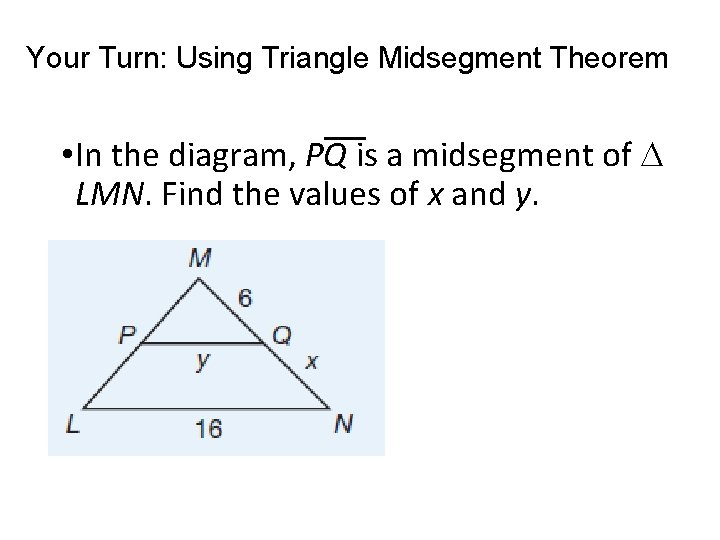
Your Turn: Using Triangle Midsegment Theorem • In the diagram, PQ is a midsegment of LMN. Find the values of x and y.

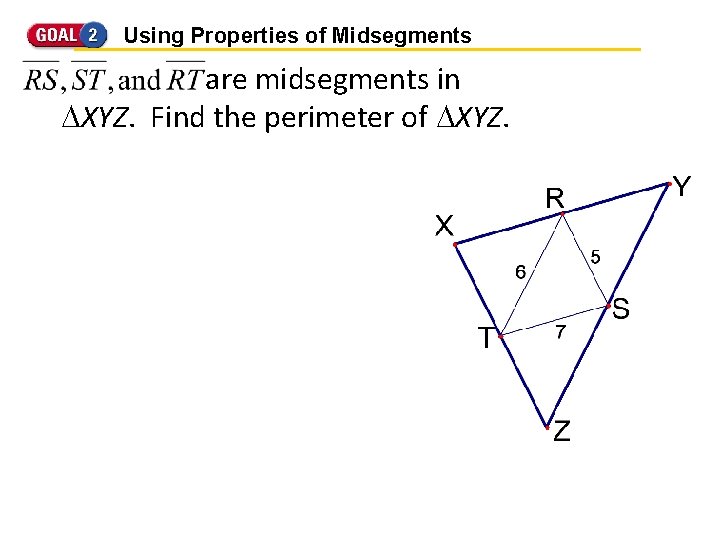
Using Properties of Midsegments are midsegments in XYZ. Find the perimeter of XYZ.

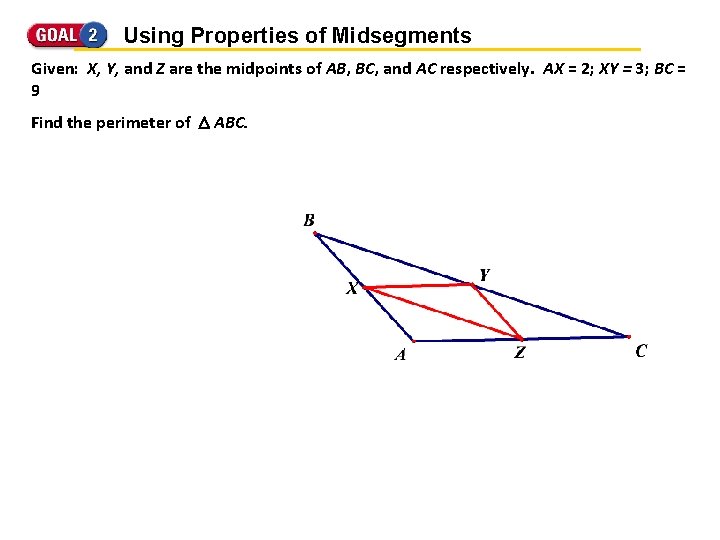
Using Properties of Midsegments Given: X, Y, and Z are the midpoints of AB, BC, and AC respectively. AX = 2; XY = 3; BC = 9 Find the perimeter of ABC.

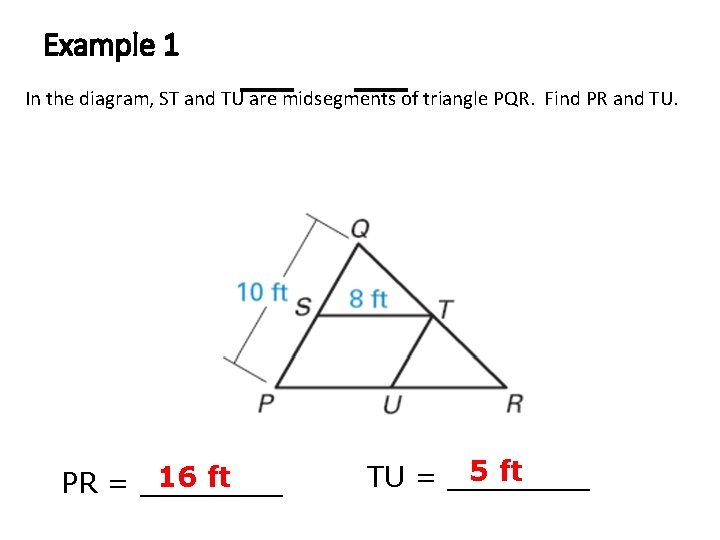
Example 1 In the diagram, ST and TU are midsegments of triangle PQR. Find PR and TU. 16 ft PR = ____ 5 ft TU = ____

Example 2 In the diagram, XZ and ZY are midsegments of triangle LMN. Find MN and ZY. 53 cm MN = ____ 14 cm ZY = ____

Midsegments Dean plans to swim the length of the lake, as shown in the photo. He counts the distances shown by counting 3 ft strides. How far would Dean swim? 35 strides 118 strides 128 strides 118 strides 35 strides x

Bisectors in Triangles

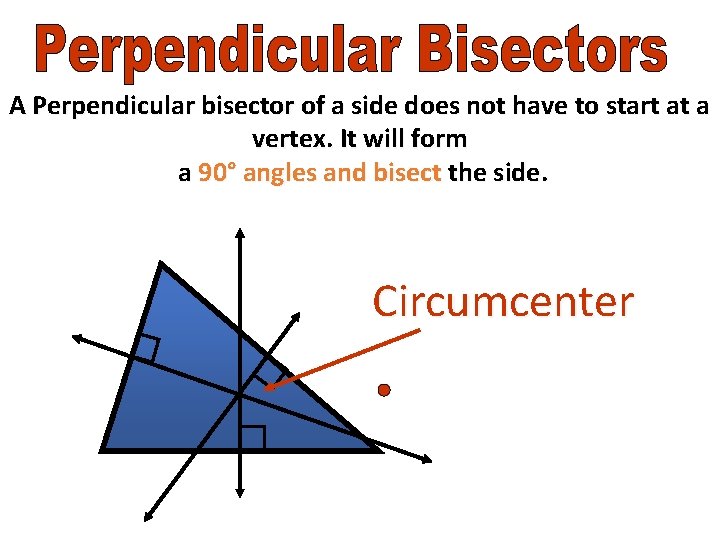
A Perpendicular bisector of a side does not have to start at a vertex. It will form a 90° angles and bisect the side. Circumcenter

When three or more lines intersect at one point, the lines are said to be concurrent.

The circumcenter of ΔABC is the center of its circumscribed circle. A circle that contains all the vertices of a polygon is circumscribed about the polygon.

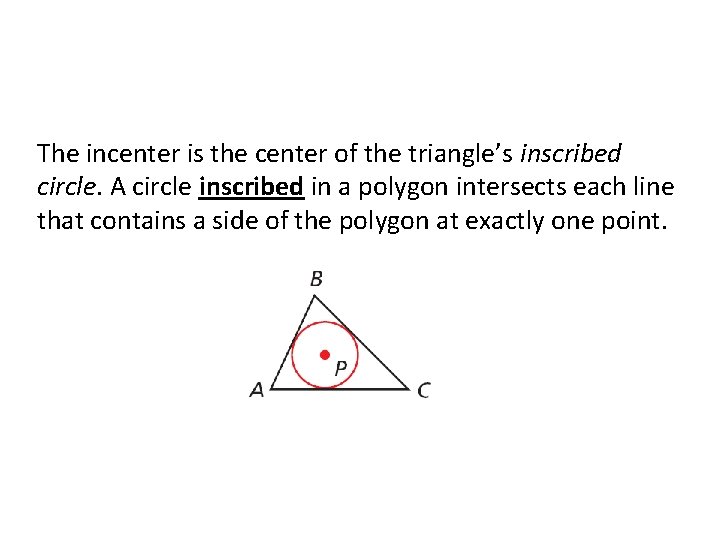
The incenter is the center of the triangle’s inscribed circle. A circle inscribed in a polygon intersects each line that contains a side of the polygon at exactly one point.

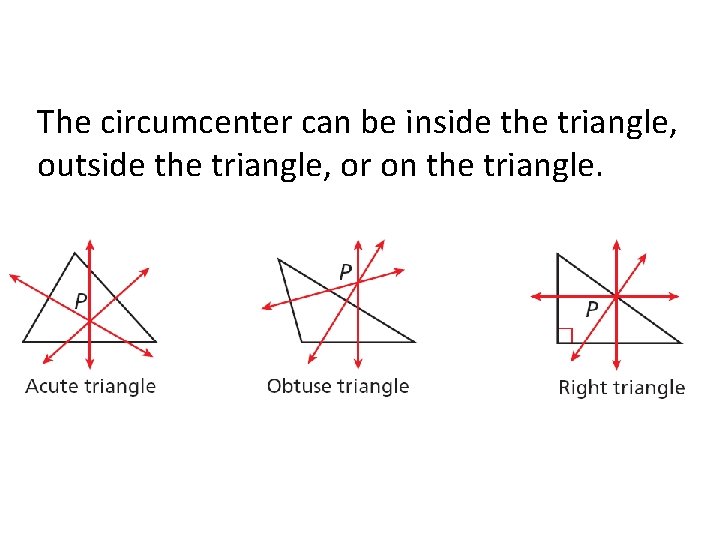
The circumcenter can be inside the triangle, outside the triangle, or on the triangle.

Example 1: Using Properties of Perpendicular Bisectors DG, EG, and FG are the perpendicular bisectors of ∆ABC. Find GC. G is the circumcenter of ∆ABC. By the Circumcenter Theorem, G is equidistant from the vertices of ∆ABC. GC = CB Circumcenter Thm. GC = 13. 4 Substitute 13. 4 for GB.

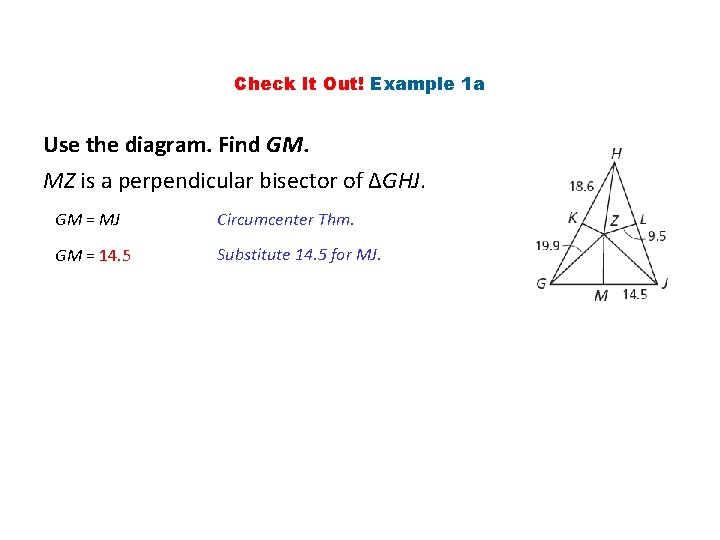
Check It Out! Example 1 a Use the diagram. Find GM. MZ is a perpendicular bisector of ∆GHJ. GM = MJ Circumcenter Thm. GM = 14. 5 Substitute 14. 5 for MJ.

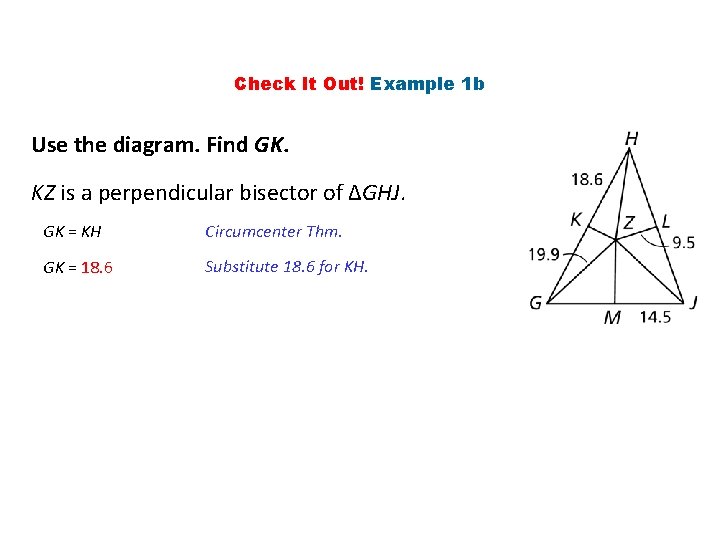
Check It Out! Example 1 b Use the diagram. Find GK. KZ is a perpendicular bisector of ∆GHJ. GK = KH Circumcenter Thm. GK = 18. 6 Substitute 18. 6 for KH.

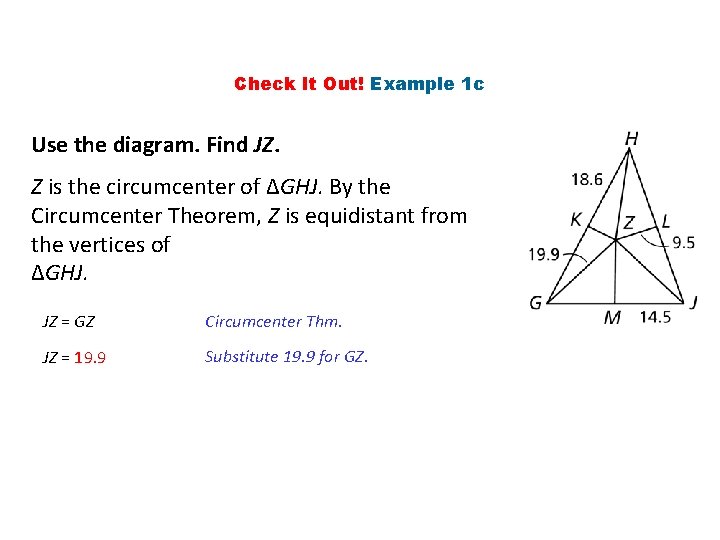
Check It Out! Example 1 c Use the diagram. Find JZ. Z is the circumcenter of ∆GHJ. By the Circumcenter Theorem, Z is equidistant from the vertices of ∆GHJ. JZ = GZ Circumcenter Thm. JZ = 19. 9 Substitute 19. 9 for GZ.

Example 2: Finding the Circumcenter of a Triangle Find the circumcenter of ∆HJK with vertices H(0, 0), J(10, 0), and K(0, 6). Step 1 Graph the triangle.

Example 2 Continued Step 2 Find equations for two perpendicular bisectors. Since two sides of the triangle lie along the axes, use the graph to find the perpendicular bisectors of these two sides. The perpendicular bisector of HJ is x = 5, and the perpendicular bisector of HK is y = 3.

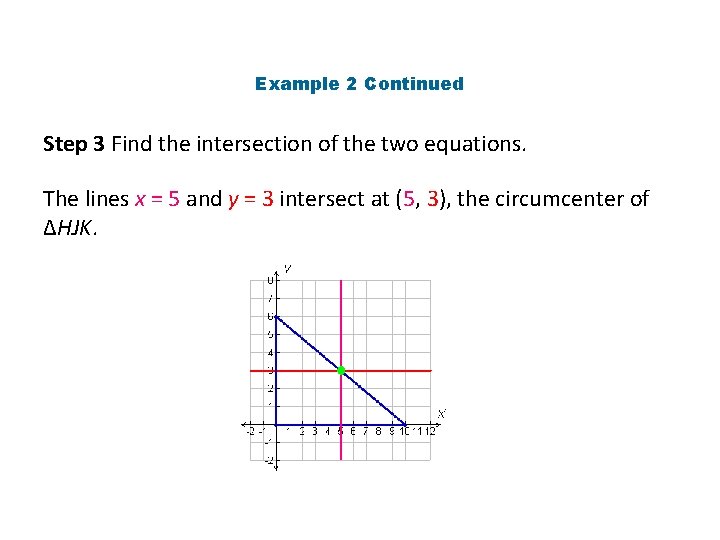
Example 2 Continued Step 3 Find the intersection of the two equations. The lines x = 5 and y = 3 intersect at (5, 3), the circumcenter of ∆HJK.

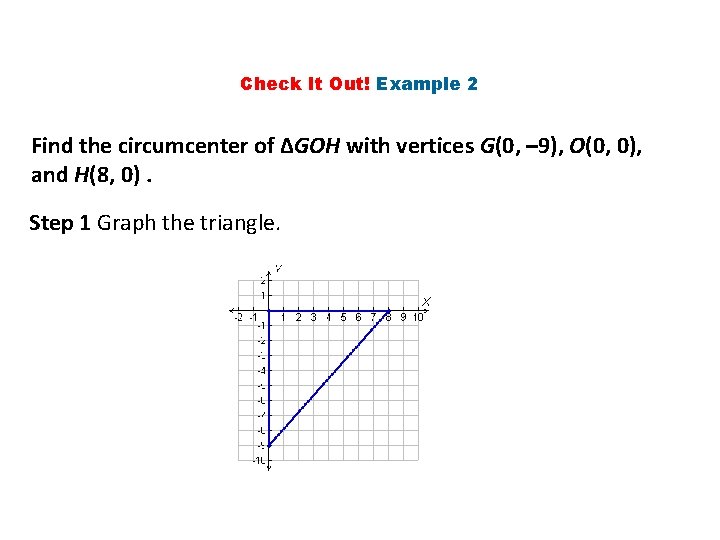
Check It Out! Example 2 Find the circumcenter of ∆GOH with vertices G(0, – 9), O(0, 0), and H(8, 0). Step 1 Graph the triangle.

Check It Out! Example 2 Continued Step 2 Find equations for two perpendicular bisectors. Since two sides of the triangle lie along the axes, use the graph to find the perpendicular bisectors of these two sides. The perpendicular bisector of GO is y = – 4. 5, and the perpendicular bisector of OH is x = 4.

Check It Out! Example 2 Continued Step 3 Find the intersection of the two equations. The lines x = 4 and y = – 4. 5 intersect at (4, – 4. 5), the circumcenter of ∆GOH.

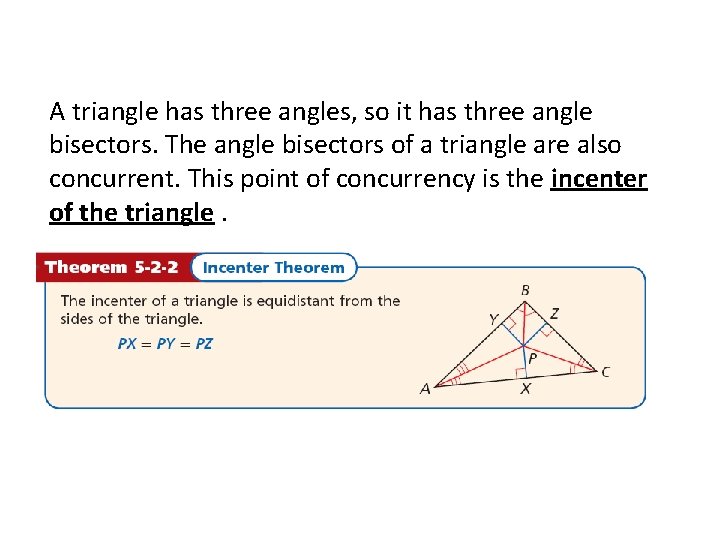
A triangle has three angles, so it has three angle bisectors. The angle bisectors of a triangle are also concurrent. This point of concurrency is the incenter of the triangle.

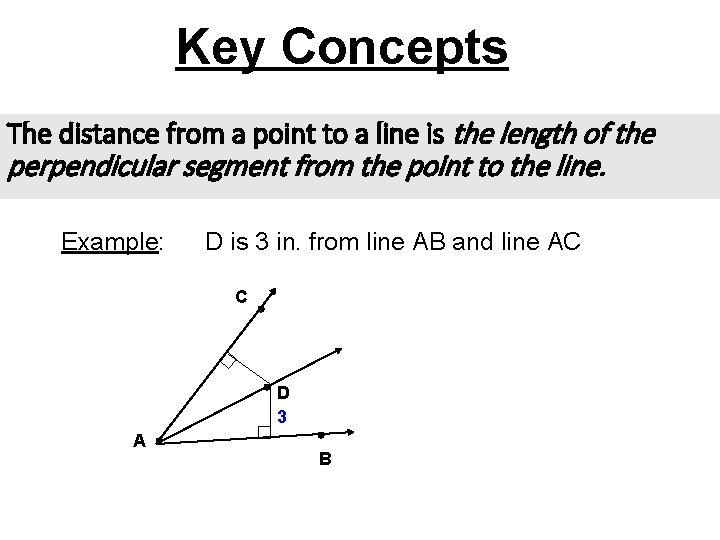
Key Concepts The distance from a point to a line is the length of the perpendicular segment from the point to the line. Example: D is 3 in. from line AB and line AC C D 3 A B

Example Using the Angle Bisector Theorem. Find x, FB and FD in the diagram at the right. Show steps to find x, FB and FD: A 2 x + 5 B F C D 7 x - 35 E

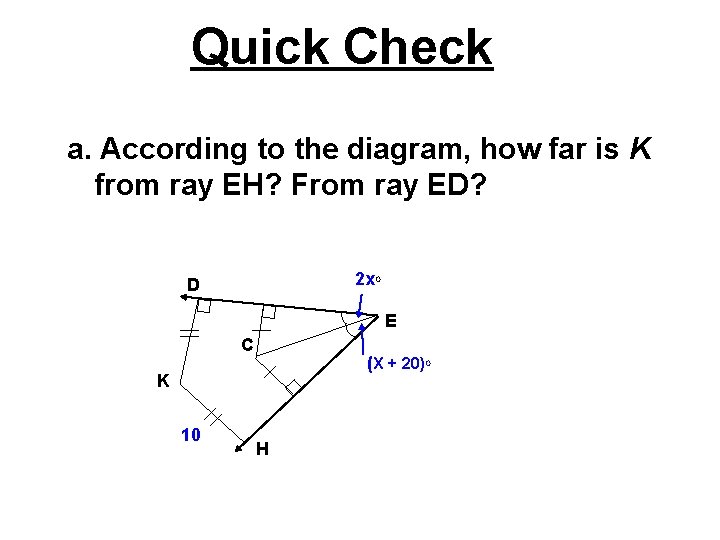
Quick Check a. According to the diagram, how far is K from ray EH? From ray ED? 2 x. O D E C (X + 20)O K 10 H

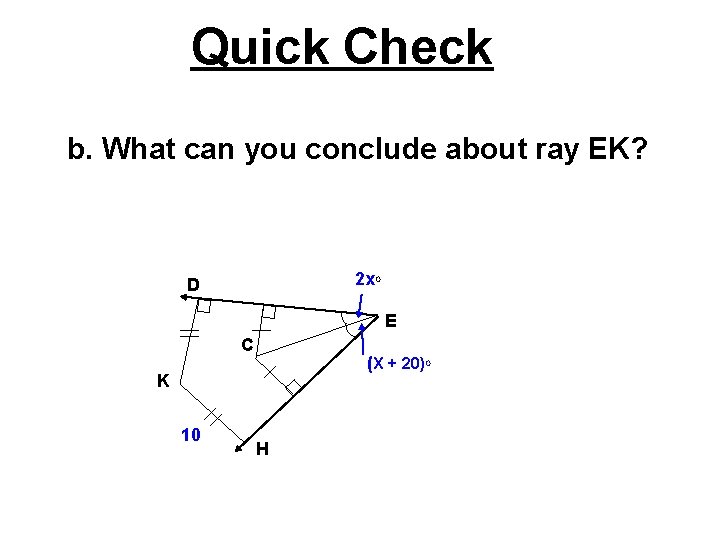
Quick Check b. What can you conclude about ray EK? 2 x. O D E C (X + 20)O K 10 H

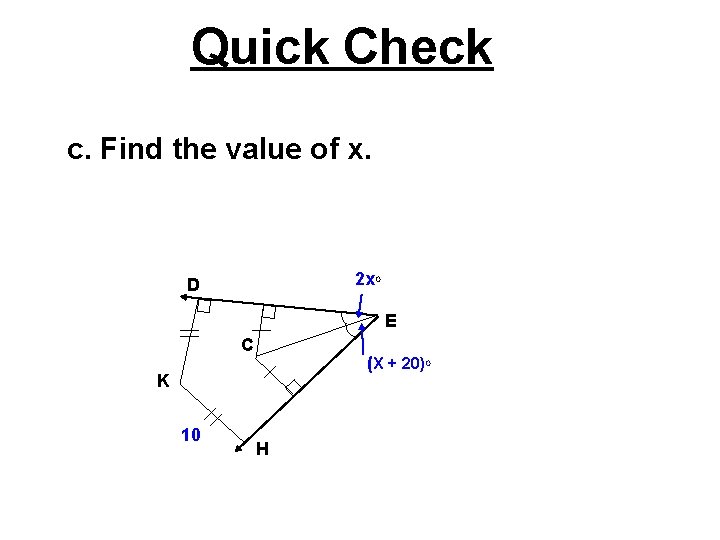
Quick Check c. Find the value of x. 2 x. O D E C (X + 20)O K 10 H

Quick Check d. Find m<DEH. 2 x. O D E C (X + 20)O K 10 H

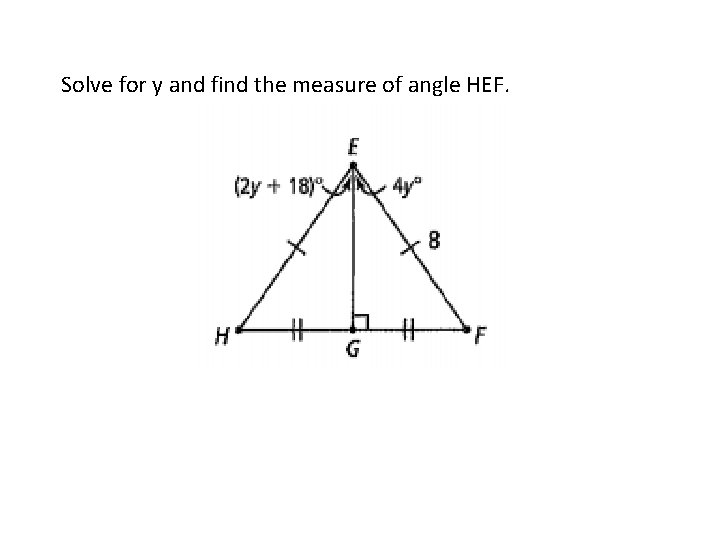
Solve for y and find the measure of angle HEF.

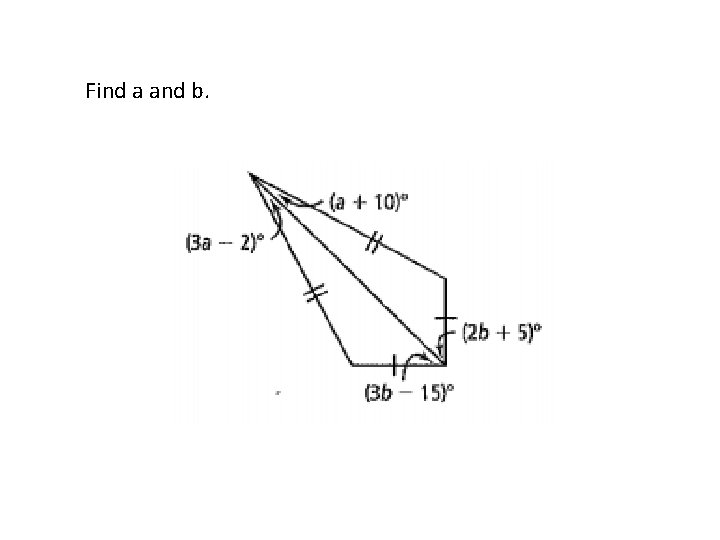
Find a and b.