Ideal diatomic gas internal degrees of freedom Polyatomic

Ideal diatomic gas: internal degrees of freedom • Polyatomic species can store energy in a variety of ways: – translational motion – rotational motion – vibrational motion – electronic excitation Each of these modes has its own manifold of energy states, how do we cope? 1

Internal modes: separability of energies • Assume molecular modes are separable – treat each mode independent of all others – i. e. translational independent of vibrational, rotational, electronic, etc Entirely true for translational modes Vibrational modes are independent of: – rotational modes under the rigid rotor assumption – electronic modes under the Born. Oppenheimer approximation 2

Internal modes: separability of energies Thus, a molecule that is moving at high speed is not forced to vibrate rapidly or rotate very fast. An isolated molecule which has an excess of any one energy mode cannot divest itself of this surplus except at collision with another molecule. The number of collisions needed to equilibrate modes varies from a few (ten or so) for rotation, to many (hundreds) for vibration. 3

Internal modes: separability of energies Thus, the total energy of a molecule j: 4

Weak coupling: factorising the energy modes • Admits there is some energy interchange – in order to establish and maintain thermal equilibrium • But allows us to assess each energy mode as if it were the only form of energy present in the molecule • Molecular partition function can be formulated separately for each energy mode (degree of freedom) • Decide later how individual partition functions should be combined together to form the overall molecular partition function 5

Weak coupling: factorising the energy modes • Imagine an assembly of N particles that can store energy in just two weakly coupled modes a and w • Each mode has its own manifold of energy states and associated quantum numbers • A given particle can have: - a-mode energy associated with quantum number k - w-mode energy associated with quantum number r 6

Weak coupling: factorising the energy modes The overall partition function, qtot: expanding we would get: 7

Weak coupling: factorising the energy modes but e(a+b) = ea. eb, therefore: each term in every row has a common factor of in the first row, in the second, and so on. Extracting these factors row by row: 8

Weak coupling: factorising the energy modes the terms in parentheses in each row are identical and form the summation: 9

Weak coupling: factorising the energy modes If energy modes are separable then we can factorise the partition function and write: 10

Factorising translational energy modes Total translational energy of molecule j: which allows us to write: 11

Factorising internal energy modes Total translational energy of molecule j: using identical arguments the canonical partition function can be expressed: but how do we obtain the canonical from the molecular partition function Qtot from qtot? How does indistinguishability exert its influence? 12

Factorising internal energy modes When are particles distinguishable (having distinct configurations, and when are they indistinguishable? • Localised particles (unique addresses) are always distinguishable • Particles that are not localised are indistinguishable – Swapping translational energy states between such particles does not create distinct new configurations • However, localisation within a molecule can also confer distinguishability 13

Factorising internal energy modes When molecules i and j, each in distinct rotational and vibrational states, swap these internal states with each other a new configuration is created and both configurations have to be counted into the final sum of states for the whole system. By being identified specifically with individual molecules, the internal states are recognised as being intrinsically distinguishable. Translational states are intrinsically indistinguishable. 14

Canonical partition function, Q and thus: This conclusion assumes weak coupling. If particles enjoy strong coupling (e. g. in liquids and solutions) the argument becomes very complicated! 15

Ideal diatomic gas: Rotational partition function Assume rigid rotor for which we can write successive rotational energy levels, e. J, in terms of the rotational quantum number, J. where I is the moment of inertia of the molecule, m is the reduced mass, and B the rotational constant. 16

Ideal diatomic gas: Rotational partition function Another expression results from using the characteristic rotational temperature, qr, • 1 st energy increment = 2 kqr • 2 nd energy increment = 4 kqr 17

Ideal diatomic gas: Rotational partition function Rotational energy levels are degenerate and each level has a degeneracy g. J = (2 J+1). So: If no atoms in the atom are too light (i. e. if the moment of inertia is not too small) and if the temperature is not too low (close to 0 K), allowing appreciable numbers of rotational states to be occupied, the rotational energy levels lie sufficiently close to one another to write: 18

Ideal diatomic gas: Rotational partition function • This equation works well for heteronuclear diatomic molecules. • For homonuclear diatomics this equation overcounts the rotational states by a factor of two. 19

Ideal diatomic gas: Rotational partition function • When a symmetrical linear molecule rotates through 180 o it produces a configuration which is indistinguishable from the one from which it started. – all homonuclear diatomics – symmetrical linear molecules (e. g. CO 2, C 2 H 2) • Include all molecules using a symmetry factor s s = 2 for homonuclear diatomics, s = 1 for heteronuclear diatomics s = 2 for H 2 O, s = 3 for NH 3, s = 12 for CH 4 and C 6 H 6 20

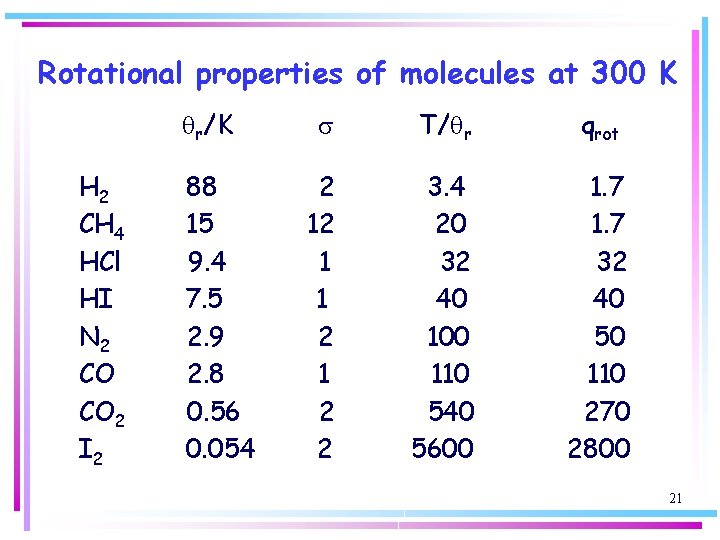
Rotational properties of molecules at 300 K qr/K H 2 CH 4 HCl HI N 2 CO CO 2 I 2 88 15 9. 4 7. 5 2. 9 2. 8 0. 56 0. 054 s T/qr qrot 2 12 1 1 2 2 3. 4 20 32 40 100 110 540 5600 1. 7 32 40 50 110 270 2800 21

Rotational canonical partition function relates the canonical partition function to the molecular partition function. Consequently, for the rotational canonical partition function we have: 22

Rotational Energy this can differentiated wrt temperature, since the second term is a constant with no T dependence 23

Rotational heat capacity this equation applies equally to all linear molecules which have only two degrees of freedom in rotation. Recast for one mole of substance and taking the T derivative yields the molar rotational heat capacity, Crot, m. Thus, when N = NA, the molar rotational energy is Urot, m 24

Rotational entropy Srot is dependent on (reduced) mass (I = mr 2), and there is also a constant in the final term, leading to: 25

Rotational entropy Typically, qrot at room T is of the order of hundreds for diatomics such as CO and Cl 2. Compare this with the almost immeasurably larger value that the translational partition function reaches. 26

Extension to polyatomic molecules • In the most general case, that of a non-linear polyatomic molecule, there are three independent moments of inertia. • Qrot must take account of these three moments – Achieved by recognising three independent characteristic rotational temperatures qr, x, qr, y, qr, z corresponding to the three principal moments of inertia Ix, Iy, Iz • With resulting partition function: 27

Conclusions • Rotational energy levels, although more widely spaced than translational energy levels, are still close enough at most temperatures to allow us to use the continuum approximation and to replace the summation of qrot with an integration. • Providing proper regard is then paid to rotational indistinguishability, by considering symmetry, rotational thermodynamic functions can be calculated. 28

Ideal diatomic gas: Vibrational partition function Vibrational modes have energy level spacings that are larger by at least an order of magnitude than those in rotational modes, which in turn, are 25— 30 orders of magnitude larger than translational modes. – cannot be simplified using the continuum approximation – do not undergo appreciable excitation at room Temp. – at 300 K Qvib ≈ 1 for light molecules 29

The diatomic SHO model We start by modelling a diatomic molecule on a simple ball and spring basis with two atoms, mass m 1 and m 2, joined by a spring which has a force constant k. The classical vibrational frequency, wosc, is given by: There is a quantum restriction on the available energies: 30

The diatomic SHO model The value is know as the zero point energy • Vibrational energy levels in diatomic molecules are always non-degenerate. • Degeneracy has to be considered for polyatomic species – Linear: 3 N-5 normal modes of vibration – Non-linear: 3 N-6 normal modes of vibration 31

Vibrational partition function, qvib • Set e 0 = 0, the ground vibrational state as the reference zero for vibrational energy. • Measure all other energies relative to reference ignoring the zero-point energy. – in calculating values of some vibrational thermodynamic functions (e. g. the vibrational contribution to the internal energy, U) the sum of the individual zero-point energies of all normal modes present must be added 32

Vibrational partition function, qvib The assumption (e 0 = 0) allows us to write: Under this assumption, qvib may be written as: a simple geometric series which yields qvib in closed form: where qvib = hw/k = characteristic vibrational 33 temperature

Vibrational partition function, qvib • Unlike the situation for rotation, qvib, can be identified with an actual separation between quantised energy levels. • To a very good approximation, since the anharmonicity correction can be neglected for low quantum numbers, the characteristic temperature is characteristic of the gap between the lowest and first excited vibrational states, and with exactly twice the zero-point energy, . 34

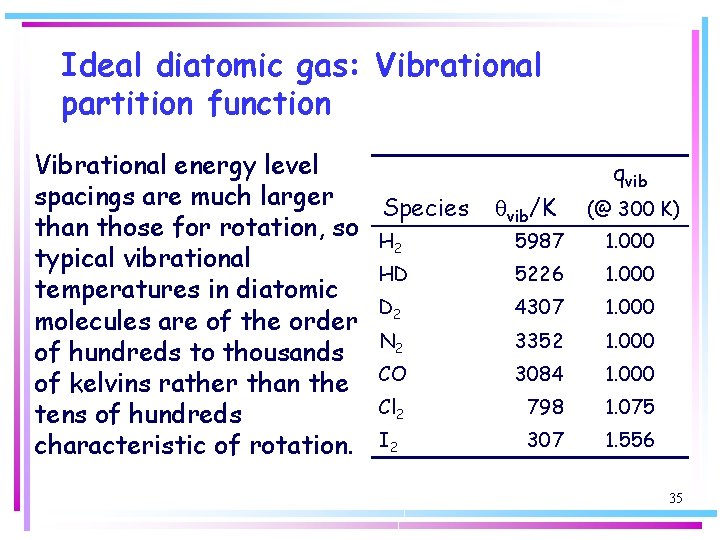
Ideal diatomic gas: Vibrational partition function Vibrational energy level spacings are much larger Species than those for rotation, so H 2 typical vibrational HD temperatures in diatomic D 2 molecules are of the order N 2 of hundreds to thousands of kelvins rather than the CO Cl 2 tens of hundreds characteristic of rotation. I 2 qvib/K qvib (@ 300 K) 5987 1. 000 5226 1. 000 4307 1. 000 3352 1. 000 3084 1. 000 798 1. 075 307 1. 556 35

Vibrational partition function, qvib • Light diatomic molecules have: – high force constants – low reduced masses • Thus: – vibrational frequencies (wosc) and characteristic vibrational temperatures (qvib) are high – just one vibrational state (the ground state) accessible at room T • the vibrational partition function qvib ≈ 1 36

Vibrational partition function, qvib • Heavy diatomic molecules have: – rather loose vibrations – Lower characteristic temperature • Thus: – appreciable vibrational excitation resulting in: • population of the first (and to a slight extent higher) excited vibrational energy state • qvib > 1 37

Vibrational partition function, qvib • Situation in polyatomic species is similar complicated only by the existence of 3 N-5 or 3 N-6 normal modes of vibration. Species CO 2 qvib/K 3360 ∏(qvib) (@ 300 K) 1. 091 1890 954(2) NH 3 4880(2) 1. 001 4780 • Some of these normal modes are degenerate 2330(2) 1360 CHCl 3 4330 2. 650 1745(2) 1090(2) 938 (1), (2), (3), … denoting individual normal modes 1, 2, 3, …etc. 523 374(2) 38

Vibrational partition function, qvib As with diatomics, only the heavier species show values of qvib appreciably different from unity. Typically, qvib is of the order of ~3000 K in many molecules. Consequently, at 300 K we have: in contrast with qrot (≈ 10) and qtrs (≈ 1030) For most molecules only the ground state is accessible for vibration 39

High T limiting behaviour of qvib At high temperature the equation High T limit gives a linear dependence of qvib with temperature. If we expand , we get: 40

T dependence of vibrational partition function As T increases, the linear dependence of qvib upon T becomes increasingly obvious 41

The canonical partition function, Qvib Using we can find the first differential of ln. Q with respect to temperature to give: 42

The vibrational energy, Uvib This is not nearly as simple as: linear molecules 43

The vibrational energy, Uvib This does reduce to the simple form at equipartition (at very high temperatures) to: (equipartition) Normally, at room T: 44

The zero-point energy • So far we have chosen the zero-point energy (1/2 hw) as the zero reference of our energy scale • Thus we must add 1/2 hw to each term in the energy ladder • For each particle we must add this same amount – Thus, for N particles we must add U(0)vib, m = 1/2 Nhw 45

Vibrational heat capacity, Cvib The vibrational heat capacity can be found using: The Einstein Equation This equation can be written in a more compact form as: 46

Vibrational heat capacity, Cvib FE with the argument qvib/T is the Einstein function The Einstein function 47

The Einstein heat capacity low T High T 48

The Einstein function • The Einstein function has applications beyond normal modes of vibration in gas molecules. • It has an important place in the understanding of lattice vibrations on thermal behaviour of solids • It is central to one of the earliest models for the heat capacity of solids 49

The vibrational entropy, Svib • We know thus: and N = NA for one mole, 50

Variation of vibrational entropy with reduced temperature 51

Electronic partition function • Characteristic electronic temperatures, qel, are of the order of several tens of thousands of kelvins. • Excited electronic states remain unpopulated unless the temperature reaches several thousands of kelvins. • Only the first (ground state) term of the electronic partition function need ever be considered at temperatures in the range from ambient to moderately high. 52

Electronic partition function It is tempting to decide that qel will not be a significant factor. Once we assign e 0 = 0, we might conclude that: To do so would be unwise! One must consider degeneracy of the ground electronic state. 53

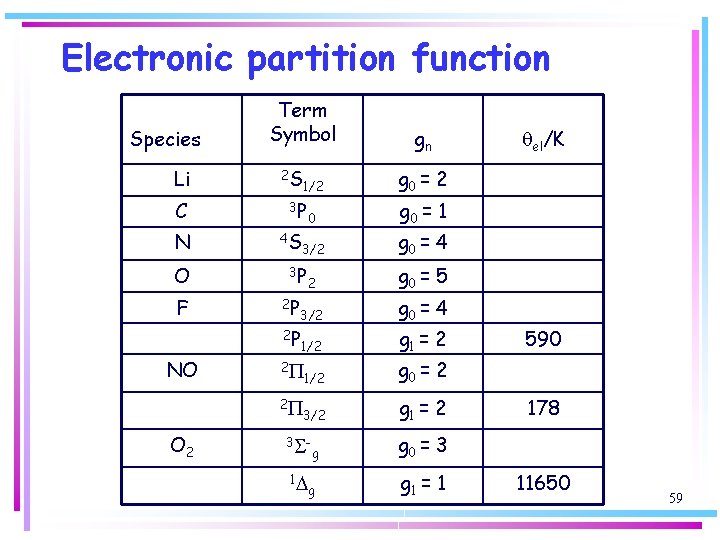
Electronic partition function The correct expression to use in place of the previous expression is of course: Most molecules and stable ions have nondegenerate ground states. A notable exception is molecular oxygen, O 2, which has a ground state degeneracy of 3. 54

Electronic partition function Atoms frequently have ground states that are degenerate. Degeneracy of electronic states determined by the value of the total angular momentum quantum number, J. Taking the symbol G as the general term in the Russell—Saunders spin-orbit coupling approximation, we denote the spectroscopic state of the ground state of an atom as: spectroscopic atom ground state = (2 S+1)G J 55

Electronic partition function spectroscopic atom ground state = (2 S+1)GJ where S is the total spin angular momentum quantum number which gives rise to the term multiplicity (2 S+1). The degeneracy, g 0, of the electronic ground states in atoms is related to J through: g 0 = 2 J+1 (atoms) 56

Electronic partition function For diatomic molecules the term symbols are made up in much the same way as for atoms. • Total orbital angular momentum about the inter-nuclear axis. Determines the term symbol used for the molecule (S, P, D, etc. corresponding to S, P, D, etc. in atoms). As with atoms, the term multiplicity (2 S+1) is added as a superscript to denote the multiplicity of the molecular term. 57

Electronic partition function In the case of molecules it is this term multiplicity that represents the degeneracy of the electronic state. For diatomic molecules we have: spectroscopic molecular ground state = (2 S+1)G for which the ground-state degeneracy is: g 0 = 2 S + 1 (molecules) 58

Electronic partition function Species Li C N O F Term Symbol 2 S 3 P 4 S 2 P g 0 = 1 3/2 g 0 = 4 2 g 0 = 5 3/2 g 0 = 4 1/2 2 P O 2 g 1 = 2 1/2 g 0 = 2 3/2 g 1 = 2 2 P g g 0 = 3 g g 1 = 1 3 S 1 D qel/K g 0 = 2 0 3 P 2 P NO 1/2 gn 590 178 11650 59

Electronic partition function Where the energy gap between the ground and the first excited electronic state is large the electronic partition function simply takes the value g 0. When the ground-state to first excited state gap is not negligible compared with k. T (qel/T is not very much less than unity) it is necessary to consider the first excited state. The electronic partition function becomes: 60

Electronic partition function For F atom at 1000 K we have: For NO molecule at 1000 K we have: 61