Equations for ideal gases The ideal gas equation

Equations for ideal gases The ideal gas equation and its variant for N molecules Relates pressure to the density of a gas and root mean square velocity. You may have to manipulate this one Relates absolute temperature to average molecular energy

Particle in a Box Deriving

The particle in a box • The idea is to derive an expression for to relate the pressure and volume of a gas to the movement of the many individual molecules which make it up • We are building a MATHEMATICAL MODEL of what is happening and to do this we will need to make several assumptions

Assumptions 1. 2. 3. 4. 5. 6. Intermolecular forces are negligible except during collisions. All collisions are perfectly elastic The volume of the molecules themselves can be neglected compared with the volume occupied by the gas. The time for any collision is negligible compared with the time spent between collisions. Between collisions molecules move with uniform velocity. There is a sufficiently large number of molecules for statistics to be meaningfully applied. These conditions imply that all of the internal energy of the gas is kinetic.

• We also start with the knowledge that : 1. Pressure = Force / Area 2. Force = rate of change of momentum

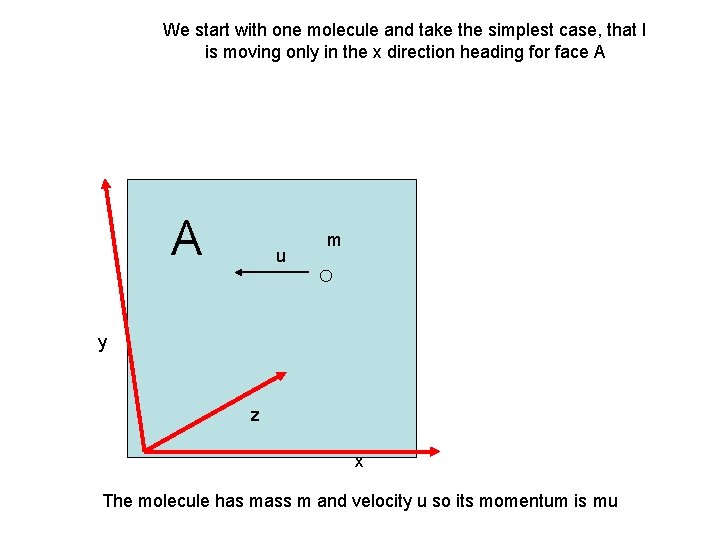
We start with one molecule and take the simplest case, that I is moving only in the x direction heading for face A A u m y z x The molecule has mass m and velocity u so its momentum is mu

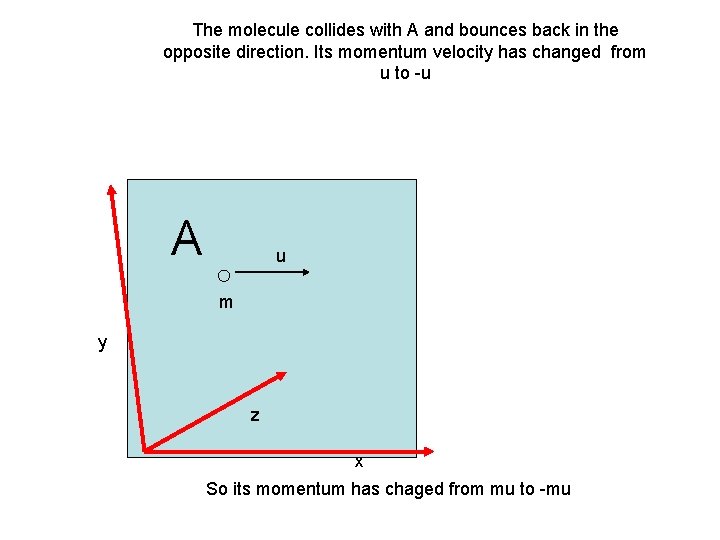
The molecule collides with A and bounces back in the opposite direction. Its momentum velocity has changed from u to -u A u m y z x So its momentum has chaged from mu to -mu

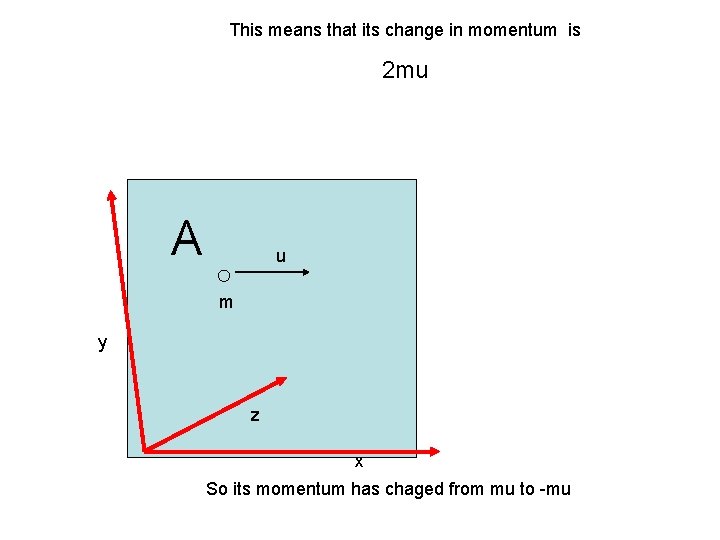
This means that its change in momentum is 2 mu A u m y z x So its momentum has chaged from mu to -mu

its rate of change of momentum is given by: this is equal to the force acting on the particle The time (∆t) between successive collisions is the time it takes to travel from wall A to the far wall of the box and back. y A m u The distance it has to travel is 2 x. x It does this travelling at velocity u

remembering that velocity is distance travelled / time taken So the time taken between collisions (∆t) is

so the rate of change of momentum of the molecule Is ie Now this is equal to the force of the wall which acts on the particle to change its momentum and by Newton’s third law this must be equal to the force of the particle acting on the wall.

So the force on the wall from this one particle is As pressure is force / area and the area of wall A is y x z The pressure on wall A due to this one molecule is y A= y x z z

This is an expression for the pressure due to 1 molecule of the ideal gas moving in the x direction. BUT there are N molecules in the gas and they have individual velocities: u 12, + u 22+ u 32, ……u. N 2

But there are three components of velocity u in the x direction , say v in the y direction and w in the z direction v w u Then taking c 2 rms = u 2 rms+ v 2 rms+w 2 rms So u 2 rms = 1/3 c 2 rms