Ideal Gas Law Describing a sample of a

Ideal Gas Law

Describing a sample of a gas • 4 variables are needed to completely describe a sample of a gas: • • Temperature Pressure Volume Amount (number of moles) of gas

Equation of State • An equation relating the macroscopic variables that describe some type of matter. • The ideal gas law is an equation of state for gases.

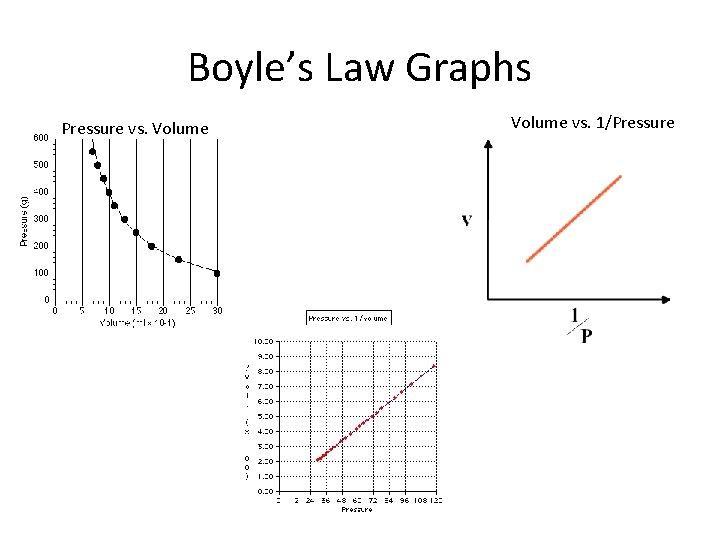
Boyle’s Law Graphs Pressure vs. Volume vs. 1/Pressure

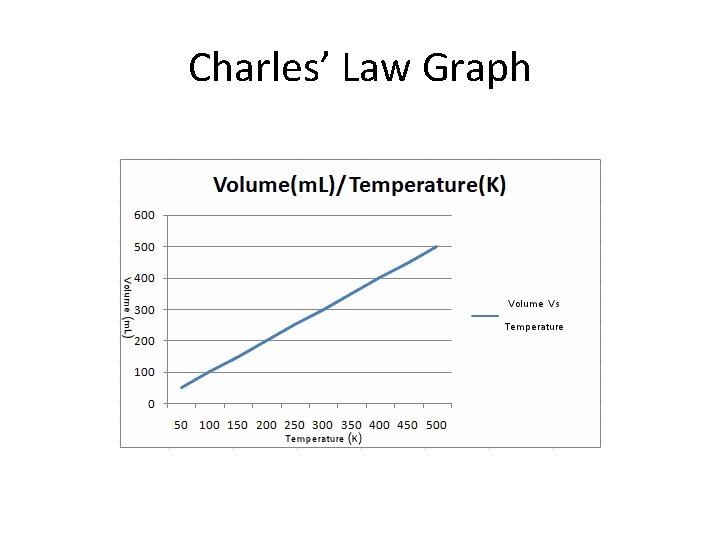
Charles’ Law Graph

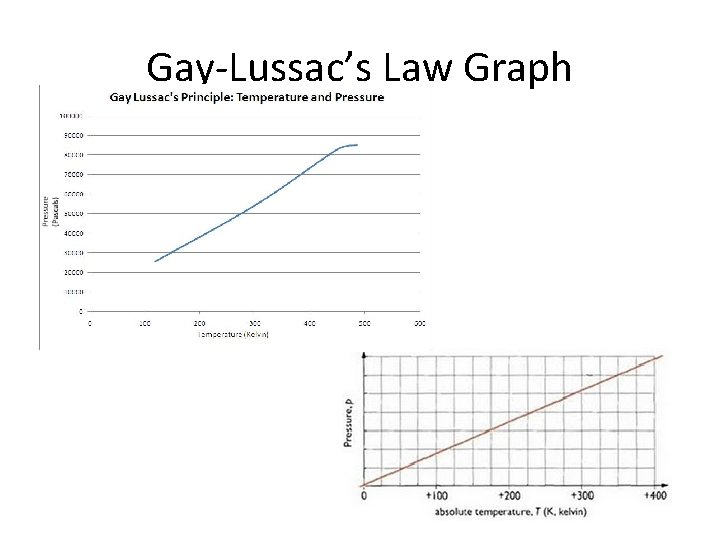
Gay-Lussac’s Law Graph

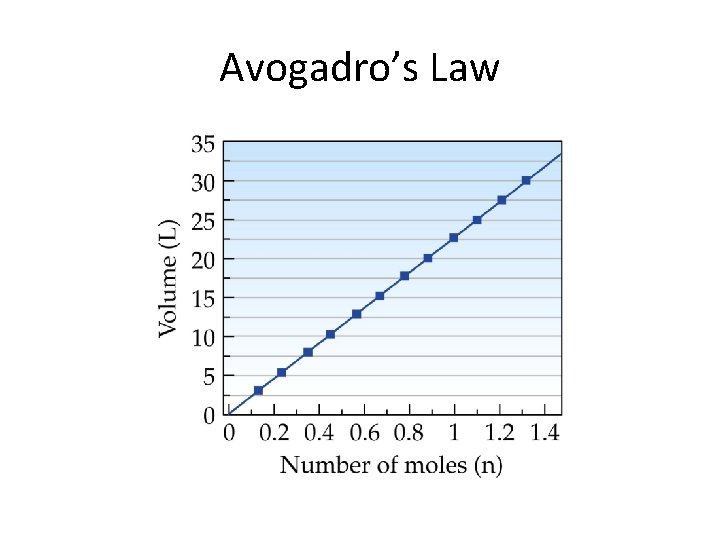
Avogadro’s Law

Recall Boyle’s Law Charles’ Law V 1/P Avogadro’s Law V T (Kelvin) V n Constant T, n Constant P, n Constant T, P So V 1/P X n X T

Ideal Gas Law • To turn a proportionality into an equation, insert a constant: V = Rn. T/P • Or multiply both sides by P: • PV = n. RT where R is the ideal gas law constant. If three of the variables are known, the 4 th can be determined. • The units of R depend on the units used for P, T, and V.

Units of R • Two common values of R: • 0. 08206 Liter Atm Mole K • 8. 314 Joules or 8. 314 Liter KPa Mole K

Problem-Solving • Most commonly used value of R: • 0. 08206 Liter Atm Mole K • • Note: Pressure must be in atm Volume must be in liters Temperature must be in Kelvins

Ideal Gas Law Problems • What pressure is exerted by 0. 75 moles of a gas at 25 C in a container with a volume of 1. 5 L? • Find the volume of 0. 85 moles of gas at a pressure of 520 torr and a temperature of 15 C. • How many moles of gas are present in a sample at 700 torr, 333 C, and occupying a volume of 452 m. L?

Extensions of Ideal Gas Law Problems • PV = n. RT • n = mass formula mass • Density = mass volume

Memorize three fundamental equations. • Substitute and rearrange as problem demands. • PV = n. RT or PV = mass RT formula mass • Rearrange to solve for mass or density volume • (P formula mass) = mass/volume = density RT

Formula mass (Identity) of gas • Formula mass = mass RT PV • Or formula mass = density RT P

Density of a gas • At STP, density of a gas = molar mass/22. 4 L • This is an easy relationship but it is only true at STP!!!

Dalton’s Law of Partial Pressures

Dalton’s Law of Partial Pressures • For a mixture of gases: • Ptot = P 1 + P 2 + P 3 + … • The total pressure of a gas mixture is the sum of the partial pressures of the component gases. The pressure exerted by each gas in an unreactive mixture is independent of the other gases in the mixture.

Addition or Subtraction Problems • Three gases, He, N 2, and Ar are present in a gas mixture. The partial pressure of He is 360 torr, of N 2 is 400 torr, and of Ar is 250 torr. Find the total pressure. • Ar is added to the above mixture until the total pressure is 1200 torr. Find the new pressure of the Argon.

Collecting Gas by Water Displacement When the water levels inside and outside the inverted container are the same, the total pressure inside the container above the water is equal to the atomspheric pressure.

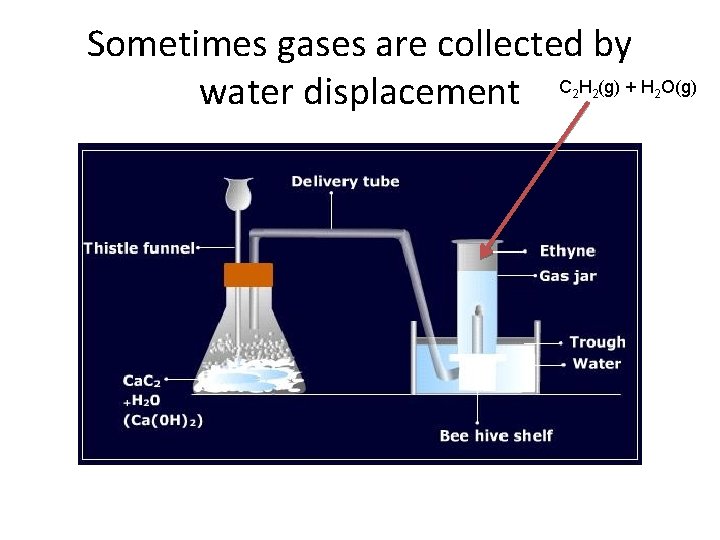
Sometimes gases are collected by water displacement C H (g) + H O(g) 2 2 2

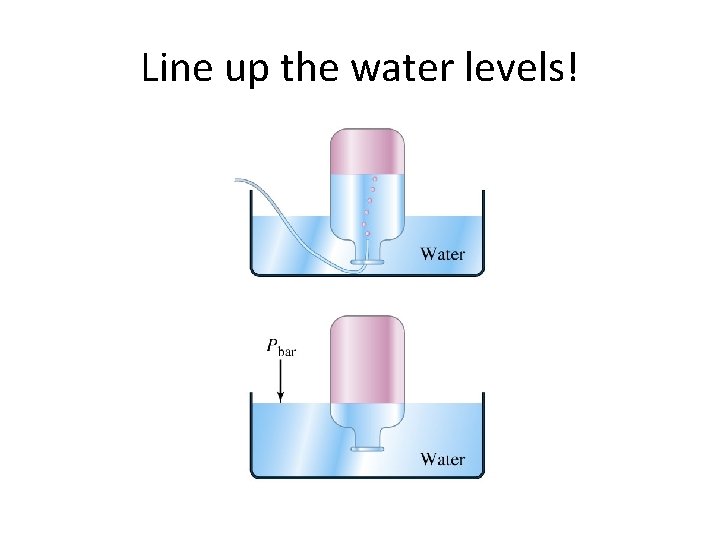
Line up the water levels!

Ptot = Pgas + Pwater • The volume of gas collects above the water, but some of the water molecules evaporate and go into the gas phase as well. • The vapor pressure of water depends only on the temperature. Look it up in a reference table and then subtract it from the total pressure.

Extension of Dalton’s Law • Since PV = n. RT then • Ptot = ntot. RT & for each component, Pi = ni. RT V V Pi = ni. RT/V Ptot ntot. RT/V Which reduces to Pi / Ptot = ni / ntot

Mole Fraction • ni / ntot is called the mole fraction = I • Pi = (ni / ntot)Ptot

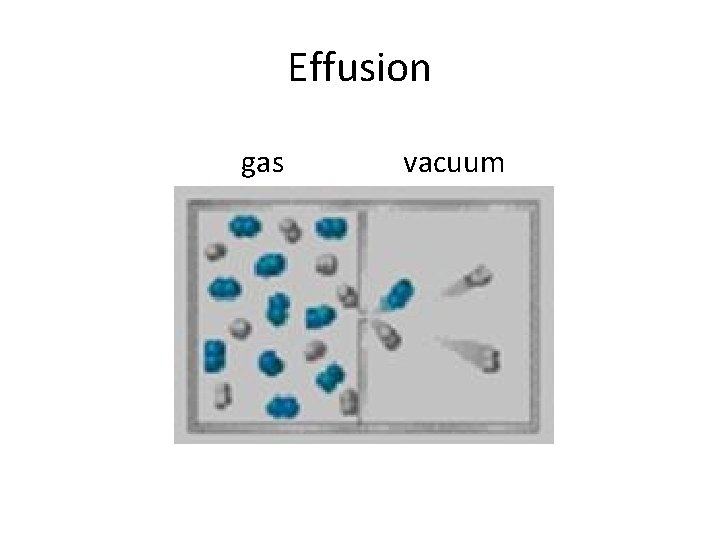
Effusion gas vacuum

Effusion • Process where molecules of a gas confined in a container randomly pass through a tiny opening in the container. • Rates of effusion can be used to determine the molar mass of a gas. • Kinetic energy of molecules in a gas depends only on temperature and equals ½ mv 2.

Effusion Two gases at the same T have the same average KE: ½ M 1 V 1 2 = ½ M 2 V 2 2 V 12 = M 2 V 22 M 1 Note: This V is the velocity of the molecules, NOT the volume of the container.

Effusion Two gases at the same T have the same average KE: ½ M 1 V 1 2 = ½ M 2 V 2 2

Graham’s Law of Effusion • The rates of effusion of gases at the same pressure and temperature are inversely proportional to the square roots of their molar masses. • The heavier gases move more slowly.

Effusion • Recall: the faster you are going, the less time it takes you to get somewhere.

Diffusion • Gradual mixing of two or more molecules due to their spontaneous, random motion. Gases are in constant, random motion and tend to move from regions of higher concentration to regions of lower concentration.

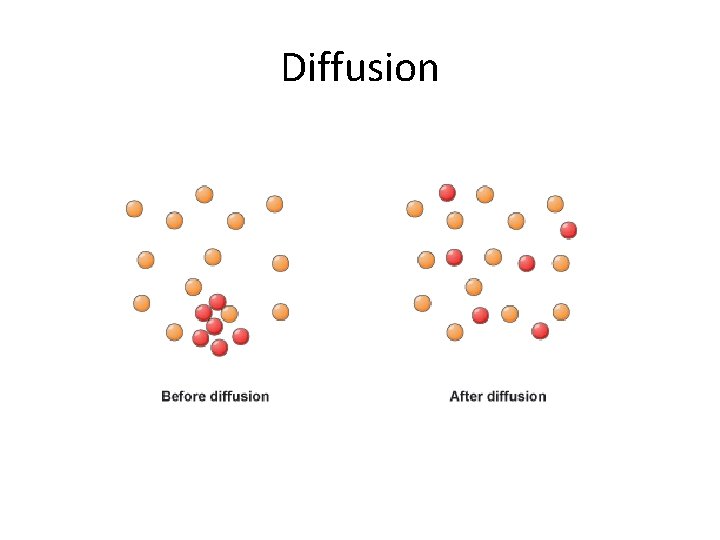
Diffusion

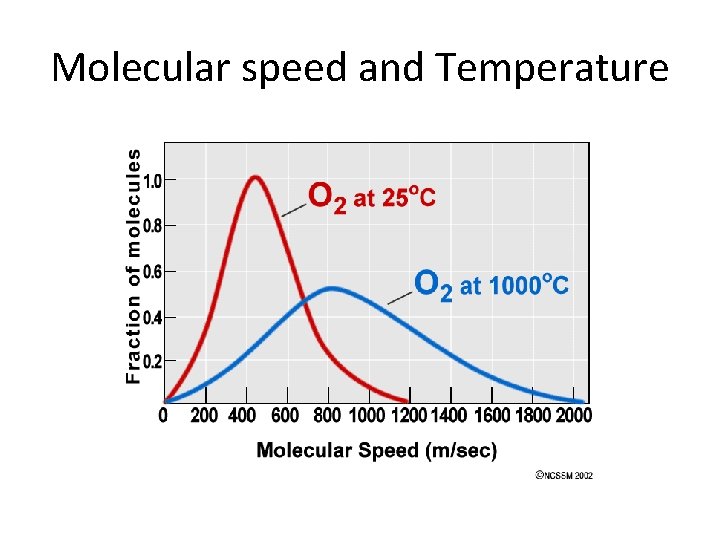
Molecular speed and Temperature

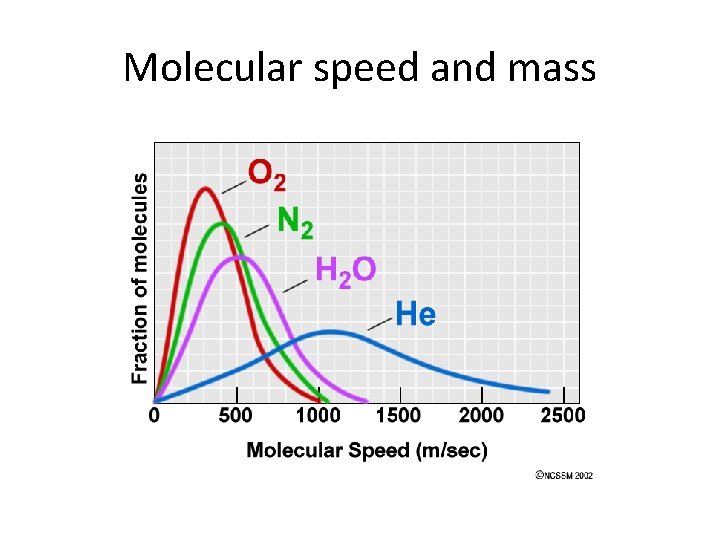
Molecular speed and mass