THERMODYNAMICS References Atkins P W Physical Chemistry Oxford























































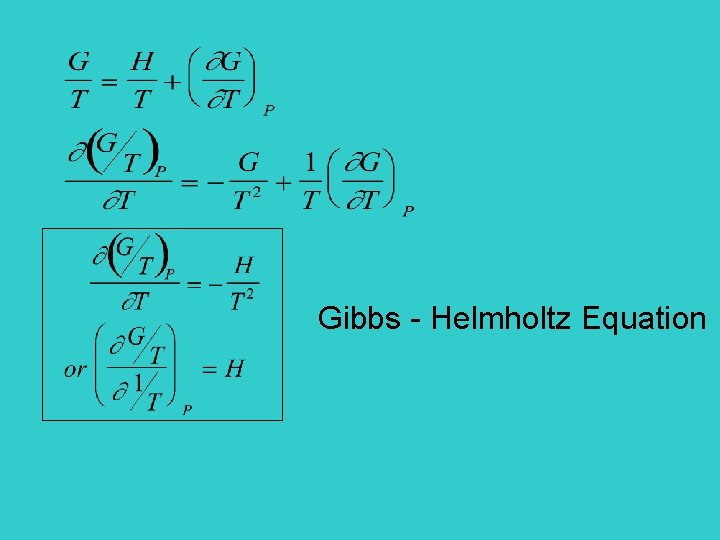









- Slides: 109

THERMODYNAMICS References · Atkins, P. W. , “Physical Chemistry”, Oxford University Press · Castellan, G. W. , “Physical Chemistry”, Addison Wesley · Levine, I. R. , “Physical Chemistry”, Mc. Graw-Hill · Laidler & Meiser, “Physical Chemistry”, Houghton Mifflin Co. · Alberty, R. A. and Silbey, R. , “Physical Chemistry”, Wiley

thermo – heat dynamics – changes definitions Events, Experiments, Observations descriptions abstract generalize no proofs no violations Laws of Thermodynamics: 0 th, 1 st, 2 nd, 3 rd Applications, Verifications

Note: · does not worry about rate of changes (kinetics) but the states before and after the change · not dealing with time

Classical Thermodynamics Marcoscopic observables T, P, V, … Statistical Thermodynamics Microscopic details dipole moment, molecular size, shape

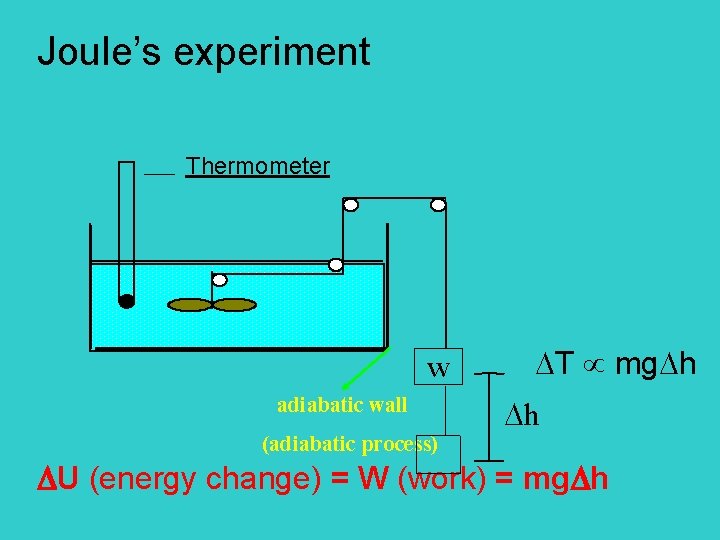
Joule’s experiment Thermometer T mg h w adiabatic wall h (adiabatic process) U (energy change) = W (work) = mg h

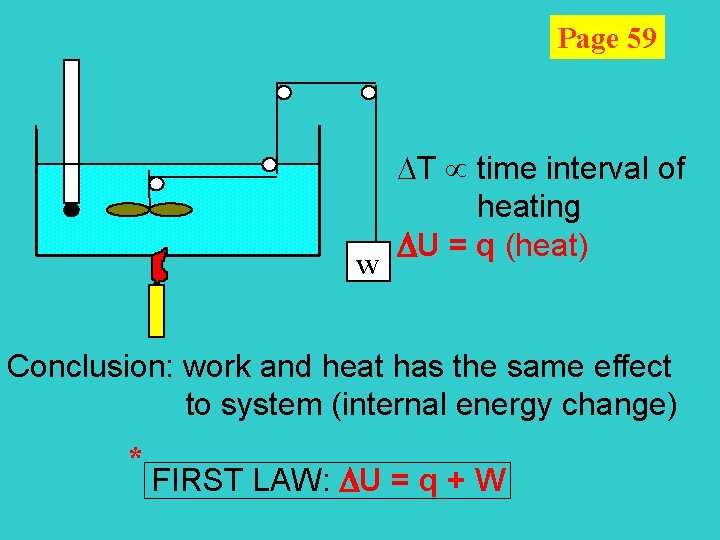
Page 59 w T time interval of heating U = q (heat) Conclusion: work and heat has the same effect to system (internal energy change) * FIRST LAW: U = q + W

U: internal energy is a state function [ = Kinetic Energy (K. E. ) + Potential Energy (P. E. ) ] q: energy transfer by temp gradient W: force distance E-potential charge surface tension distance pressure volume First Law: The internal energy of an isolated system is constant

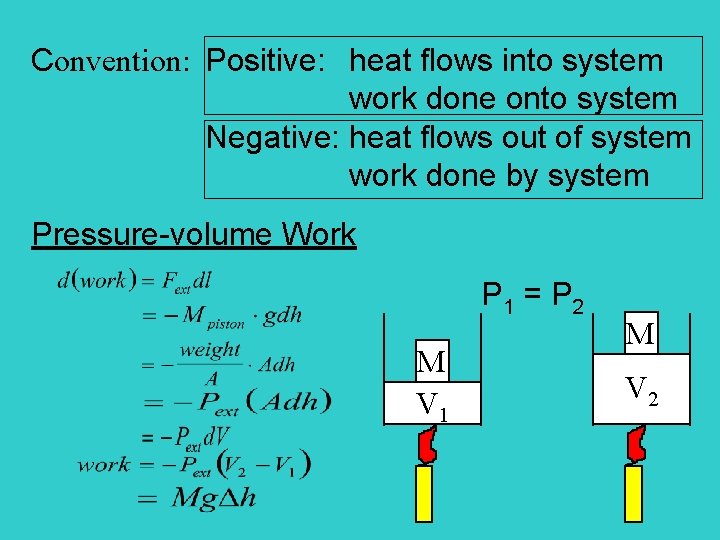
Convention: Positive: heat flows into system work done onto system Negative: heat flows out of system work done by system Pressure-volume Work P 1 = P 2 M V 1 M V 2

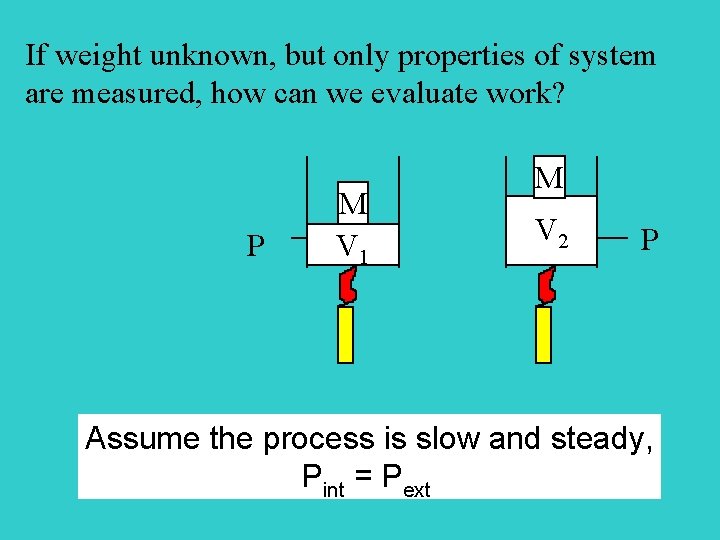
If weight unknown, but only properties of system are measured, how can we evaluate work? P M V 1 M V 2 P Assume the process is slow and steady, Pint = Pext

Free Expansion: Free expansion occurs when the external pressure is zero, i. e. there is no opposing force

Reversible change: a change that can be reversed by an infinitesimal modification of a variable. Quasi equilibrium process: Pint = Pext + d. P (takes a long time to complete) infinitesimal at any time quasi equilibrium process

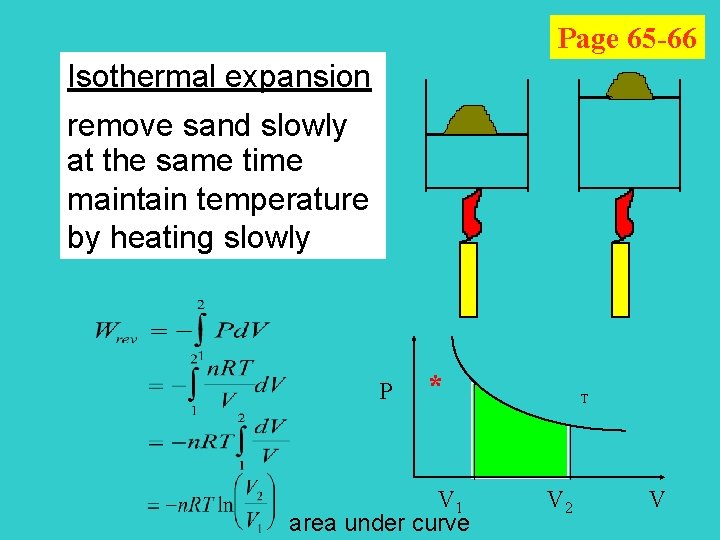
Page 64 -66 P 1 2 Example: P 1 = 200 k. Pa = P 2 V 1 = 0. 04 m 3 V 2 = 0. 1 m 3 V * what we have consider was isobaric expansion (constant pressure) other types of reversible expansion of a gas: isothermal, adiabatic

Page 65 -66 Isothermal expansion remove sand slowly at the same time maintain temperature by heating slowly P * V 1 area under curve T V 2 V

Ex. V 1 = 0. 04 m 3 P 1 = 200 k. Pa V 2 = 0. 1 m 3

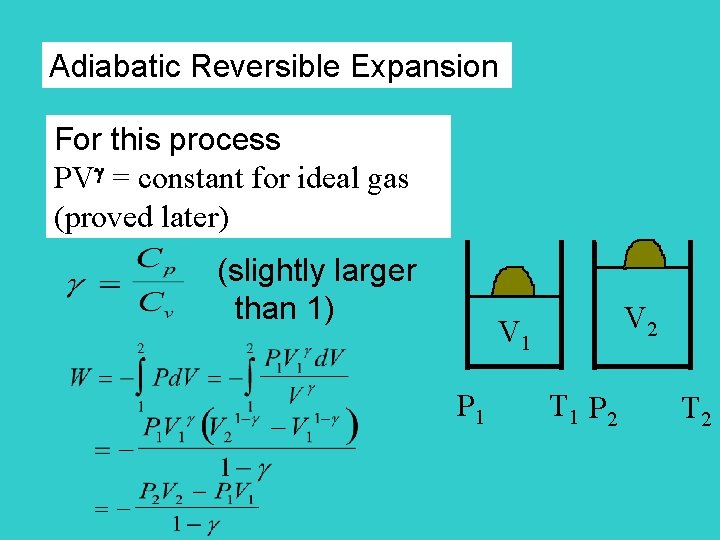
Adiabatic Reversible Expansion For this process PV = constant for ideal gas (proved later) (slightly larger than 1) V 2 V 1 P 1 T 1 P 2 T 2

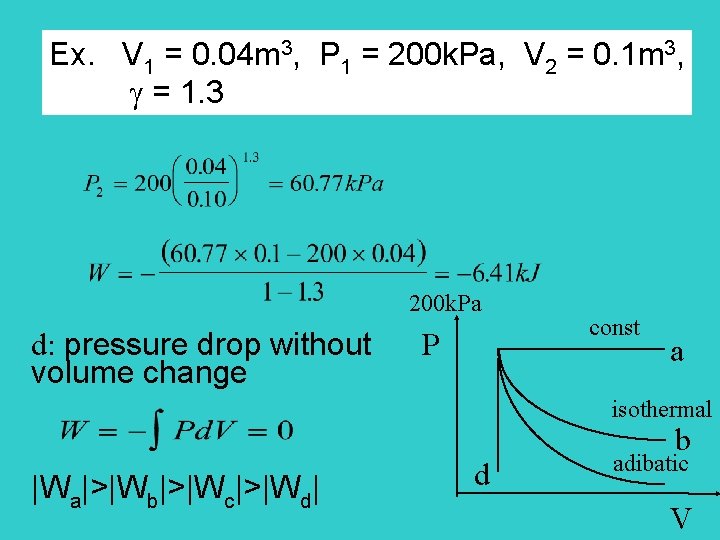
Ex. V 1 = 0. 04 m 3, P 1 = 200 k. Pa, V 2 = 0. 1 m 3, = 1. 3 200 k. Pa d: pressure drop without P volume change const a isothermal |Wa|>|Wb|>|Wc|>|Wd| d b adibatic V

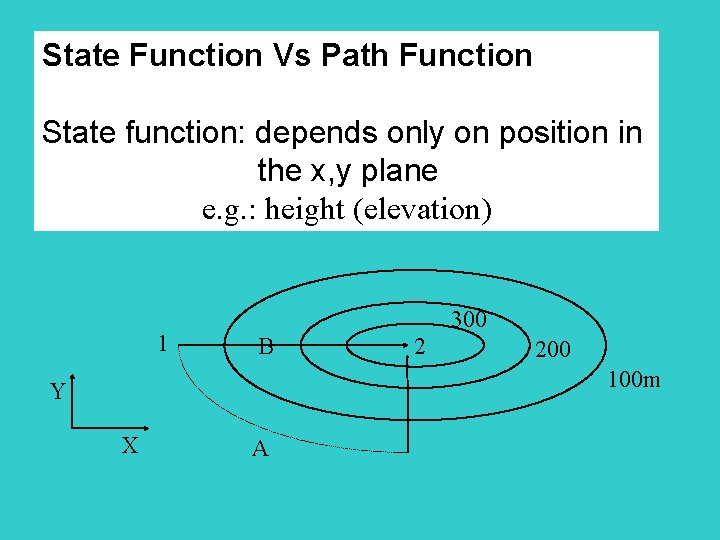
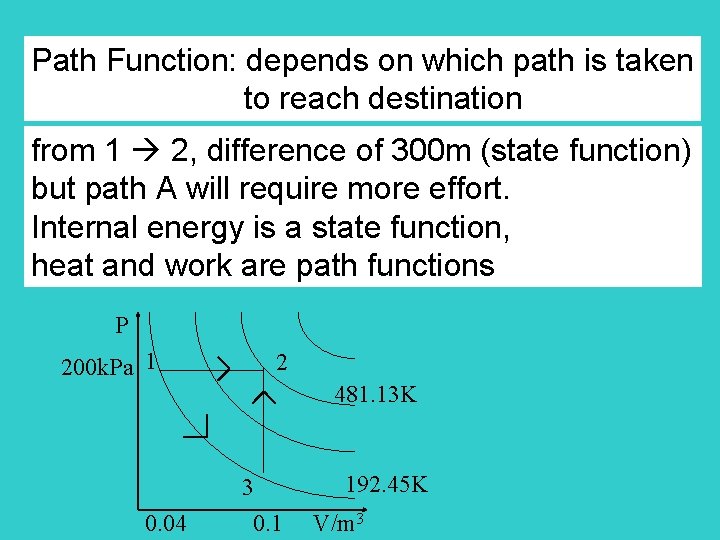
State Function Vs Path Function State function: depends only on position in the x, y plane e. g. : height (elevation) 1 300 B 2 200 100 m Y X A

Path Function: depends on which path is taken to reach destination from 1 2, difference of 300 m (state function) but path A will require more effort. Internal energy is a state function, heat and work are path functions P 200 k. Pa 1 2 481. 13 K 3 0. 04 0. 1 192. 45 K V/m 3

5 moles of monoatomic gas

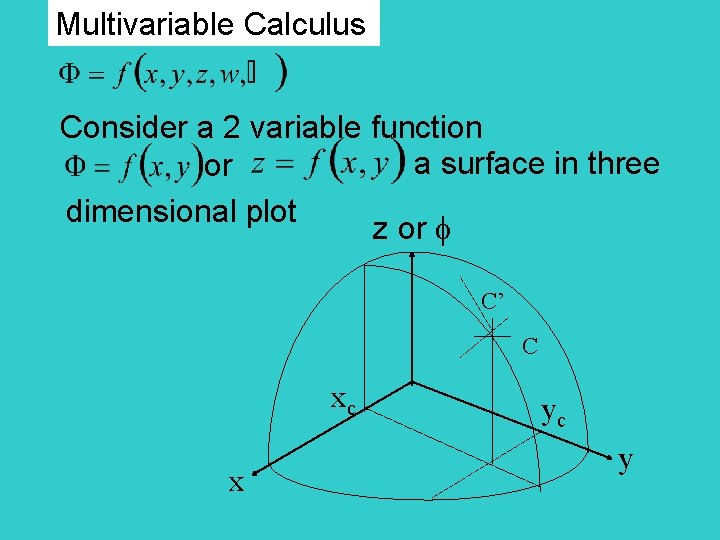
Multivariable Calculus Consider a 2 variable function a surface in three or dimensional plot z or C’ C xc x yc y

At point C, there are two slopes orthogonal to each other in constant x or constant y direction z C’ C’ z C C x=x. C y=yc y x

the change in can be calculated as a sum of two parts: change in x direction and change in y direction partial derivative w. r. t. x w. r. t. y

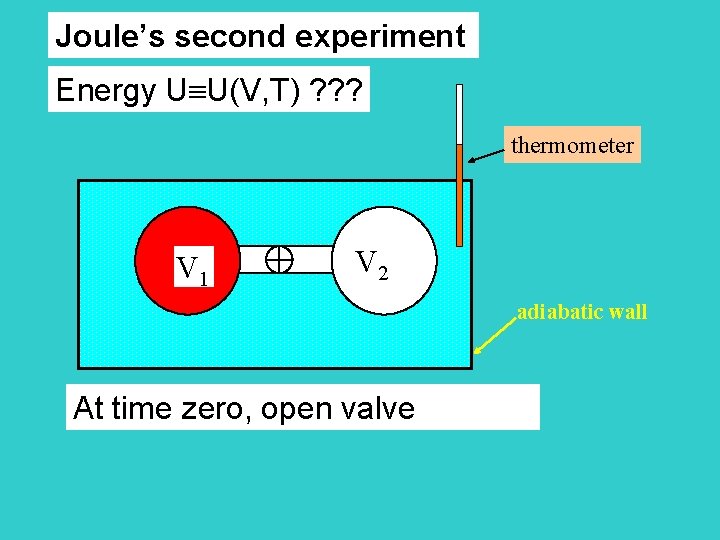
Joule’s second experiment Energy U U(V, T) ? ? ? thermometer V 1 V 2 adiabatic wall At time zero, open valve

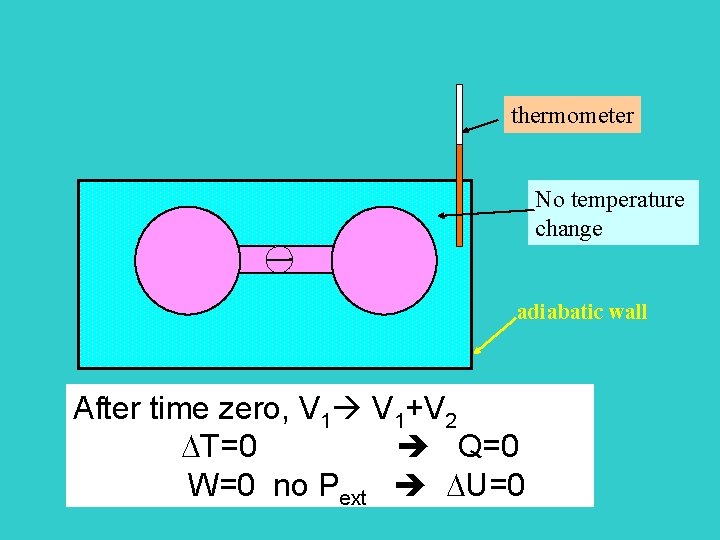
thermometer No temperature change adiabatic wall After time zero, V 1+V 2 T=0 Q=0 W=0 no Pext U=0

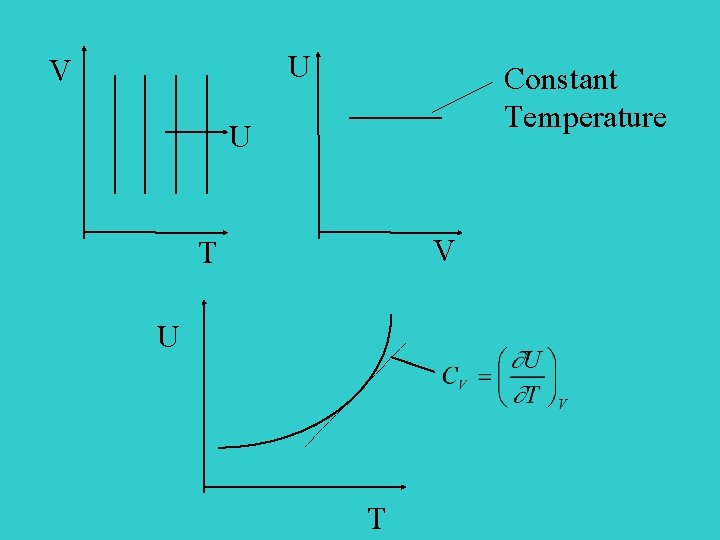
Page 99 U=U(T) Energy is only a function of temperature for ideal gas * 0 (for ideal gas) CV is constant volume heat capacity

Kinetic Model for Gases Qualitatively: • Gases consists of spheres of negligible size, far apart from one other. • Particles in ceaseless random motion; no interactions except collisions

U V Constant Temperature U V T U T

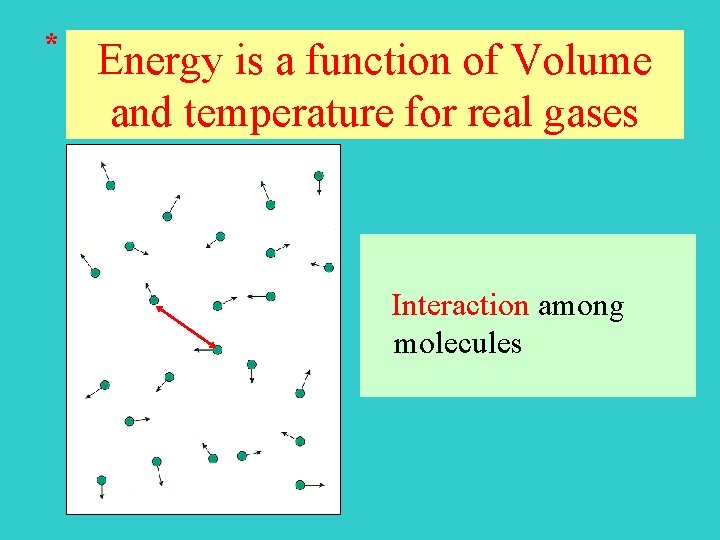
* Energy is a function of Volume and temperature for real gases Interaction among molecules

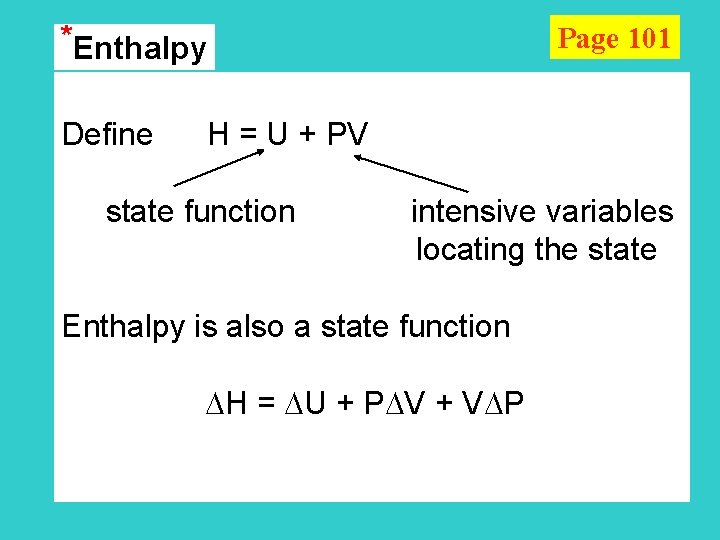
*Enthalpy Page 101 Define H = U + PV state function intensive variables locating the state Enthalpy is also a state function H = U + P V + V P

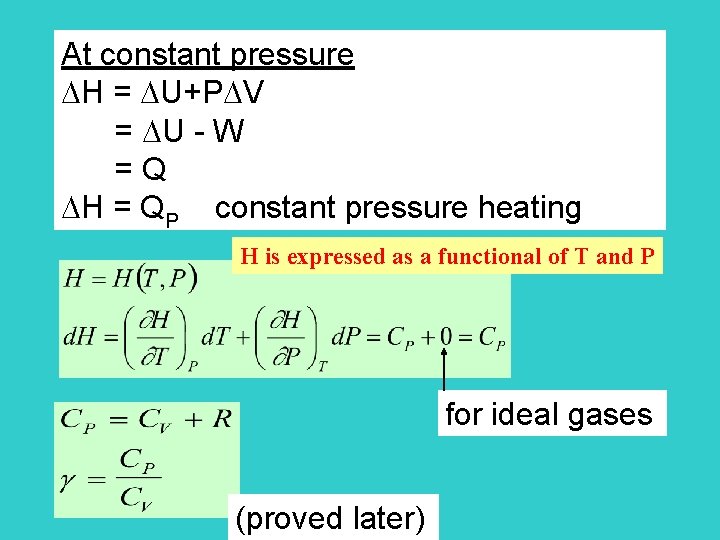
At constant pressure H = U+P V = U - W = Q H = QP constant pressure heating H is expressed as a functional of T and P for ideal gases (proved later)

Thermochemistry Heat transferred at constant volume q. V = U Heat transferred at constant pessure q. P = H Exothermic H = -ve Endothermic H = +ve

Standard states, standard conditions do not measure energies and enthalpies absolutely but only the differences, U or H The choice of standard state is purely a matter of convenience Analogy – differences in altitudes between 100 points and their elevation with respect to sea level

* What is the standard state ? The standard states of a substance at a specified temperature is its pure form at 1 bar

25 o. C, 1 bar: the most stable forms of elements assign “zero enthalpy” H o 298 = 0 used for chemical reactions

Standard enthalpy of formation Standard enthalpy change for the formation of the compound from its elements in their reference states. Reference state of an element is its most stable state at the specified temperature & 1 bar o C (s) + 2 H 2 (g) CH 4 (g) Hf = -75 k. J 289 K, 1 atm From the definition, Hfo for elements 0

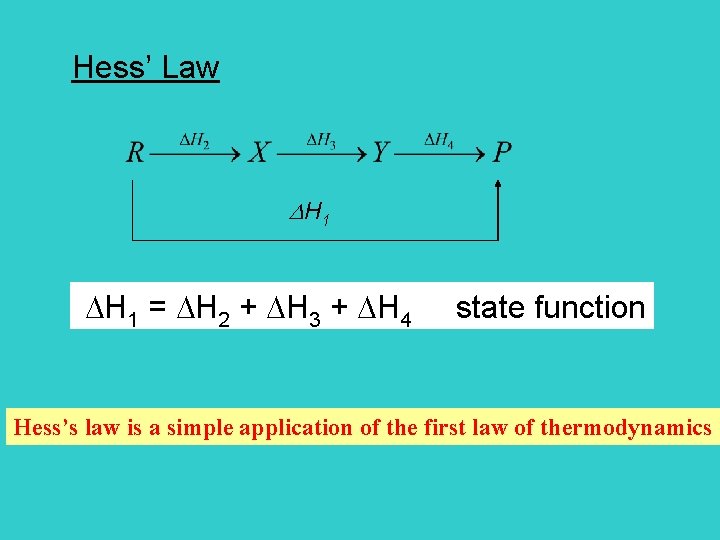
Hess’s Law The standard enthalpy of an overall reaction is the sum of the standard enthalpies of the individual reactions into which a reaction may be divided. Standard reaction enthalpy is the change in enthalpy when the reactants in their standard states change to products in their standard states.

Hess’ Law H 1 = H 2 + H 3 + H 4 state function Hess’s law is a simple application of the first law of thermodynamics

e. g. C (s) + 2 H 2 (g) CH 4 (g) H 1 o = ? 298 K, 1 atm C (s, graphite) + O 2 (g) CO 2 (g) Ho = -393. 7 k. J H 2 (g) + ½O 2(g) H 2 O (l) Ho = -285. 8 k. J CH 4 (g) + 2 O 2 (g) CO 2 (g) + 2 H 2 O (l) Ho = -890. 4 k. J H 1 o = -393. 7 + 2(-285. 8) - (-890. 4) = -75 k. J/mole

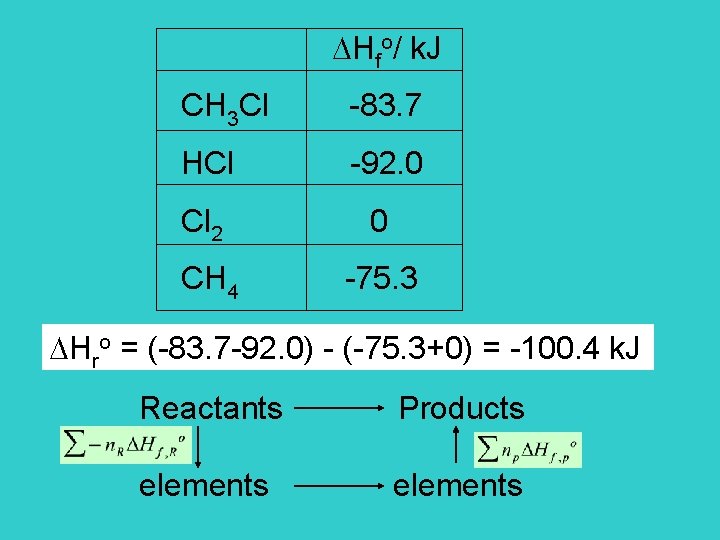
Heat of Reaction (Enthalpy of Reaction) Enthalpy change in a reaction, which may be o obtained from Hf of products and reactants Reactants Products I stoichiometric coefficient, + ve products, - ve reactants E. g. CH 4 (g) + Cl 2 (g) CH 3 Cl (g) + HCl (g)

Hfo/ k. J CH 3 Cl -83. 7 HCl -92. 0 Cl 2 0 CH 4 -75. 3 Hro = (-83. 7 -92. 0) - (-75. 3+0) = -100. 4 k. J Reactants Products elements

Page 83 2 A + B 3 C + D 0 = 3 C + D - 2 A - B Generally, 0 = J J denotes substances, J are the stoichiometric numbers *

Bond energy (enthalpy) Assumption – the strength of the bond is independent of the molecular environment in which the atom pair may occur. o C (s, graphite) + 2 H 2 (g) CH 4(g) H = -75. 4 k. J o H 2 (g) 2 H (g) H = 435. 3 k. J o C (s, graphite) C (g) H = 715. 8 k. J C (s, graphite) + 2 H 2 (g) C (g) + 4 H (g) Ho = 2(435. 3)+715. 8 = 1586. 5 k. J C (g) + 4 H (g) CH 4 (g) H = -75. 4 -1586. 5 = -1661. 9 k. J CH Bond enthalpy = 1661. 9/4 k. J = 415. 5 k. J

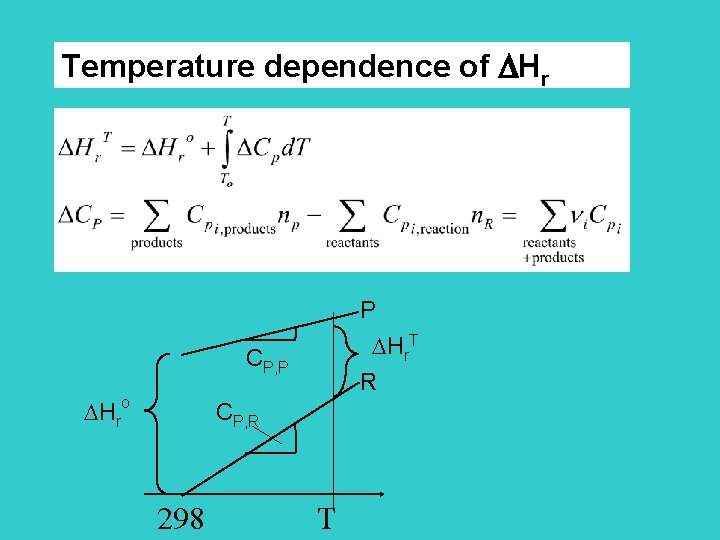
Temperature dependence of Hr P Hr. T CP, P Hro R CP, R 298 T

What is the enthalpy change for vaporization (enthalpy of vaporization) of water at 0 o. C? H 2 O (l) H 2 O (g) Ho = -241. 93 - (-286. 1) = 44. 01 k. Jmol-1 o H 2 = H + CP(T 2 -T 1) assume CP, i constant wrt T H (273) = Ho(298) + CP(H 2 O, g) - CP (H 2 O, l) (273 -298) = 44. 10 - (33. 59 -75. 33)(-25) = 43. 0 k. J/mole

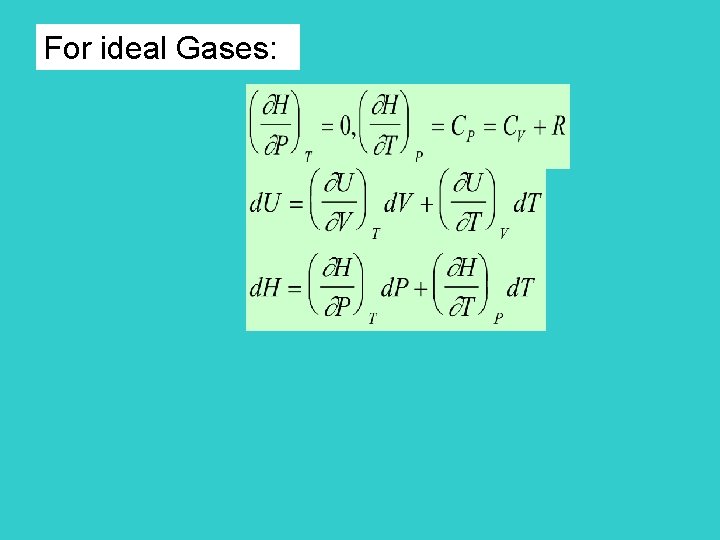
For ideal Gases:

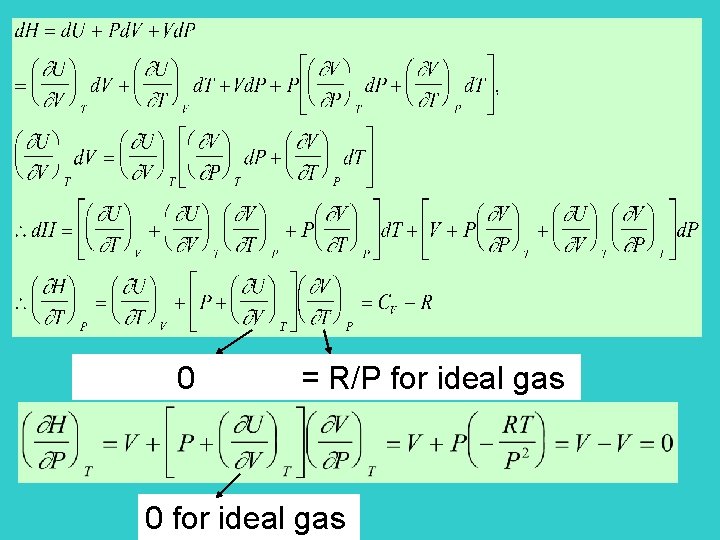
0 = R/P for ideal gas 0 for ideal gas

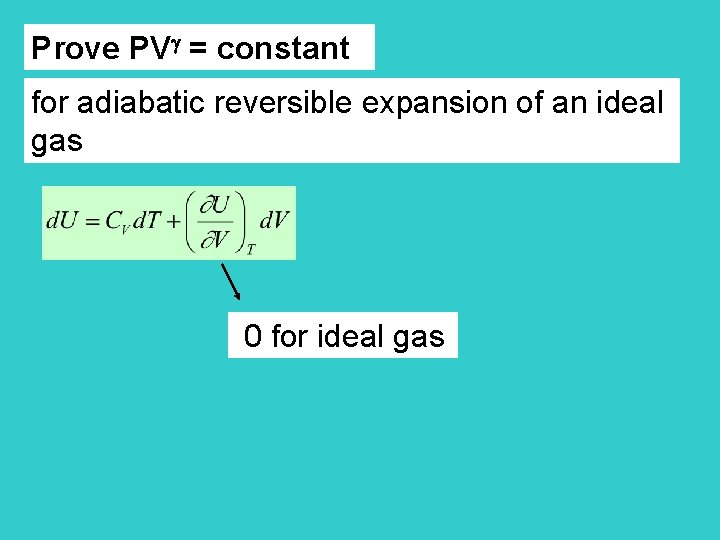
Prove PV = constant for adiabatic reversible expansion of an ideal gas 0 for ideal gas

Adiabatic expansion

Reversible vs Irreversible Non-spontaneous changes vs Spontaneous changes Reversibility vs Spontaneity First law does not predict direction of changes, cannot tell which process is spontaneous. Only U = Q + W

Second Law of Thermodynamics • Origin of the driving force of physical and chemical change • The driving force: Entropy • Application of Entropy: • Heat Engines & Refrigerators • Spontaneous Chemical Reactions • Free Energy

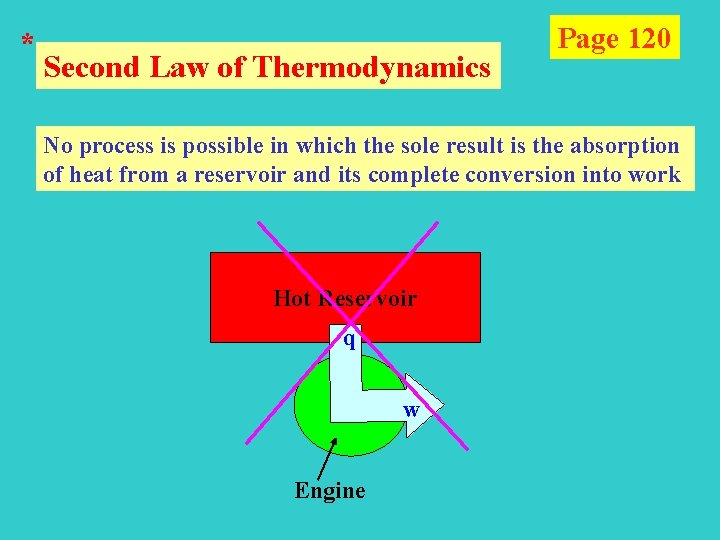
* Second Law of Thermodynamics Page 120 No process is possible in which the sole result is the absorption of heat from a reservoir and its complete conversion into work Hot Reservoir q w Engine

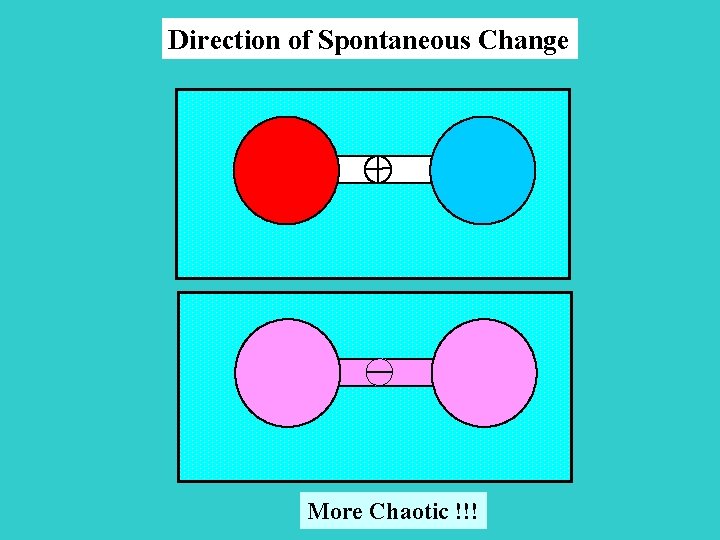
Direction of Spontaneous Change More Chaotic !!!

Spontaneous change is usually accompanied by a dispersal of energy into a disorder form, and its consequence is equivalent to heating Entropy (S) is a measurement of the randomness of the system, and is a state function! S Q S 1/T

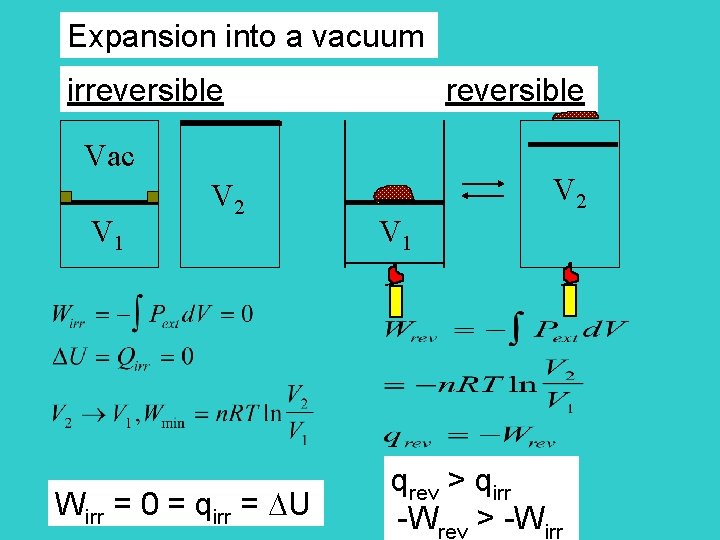
Expansion into a vacuum irreversible reversible Vac V 1 V 2 Wirr = 0 = qirr = U V 2 V 1 qrev > qirr -Wrev > -Wirr

Entropy S Page 122 For a reversible process, the change of entropy is defined as (thermodynamic definition of the entropy) * Another expression of the Second Law: The entropy of an isolated systems increases in the course of a spontaneous change: Stot > 0 where Stot is the total entropy of the isolated system

Entropy S The entropy of an isolated systems increases in the course of a reversible change: Stot = 0 where Stot is the total entropy of the isolated system

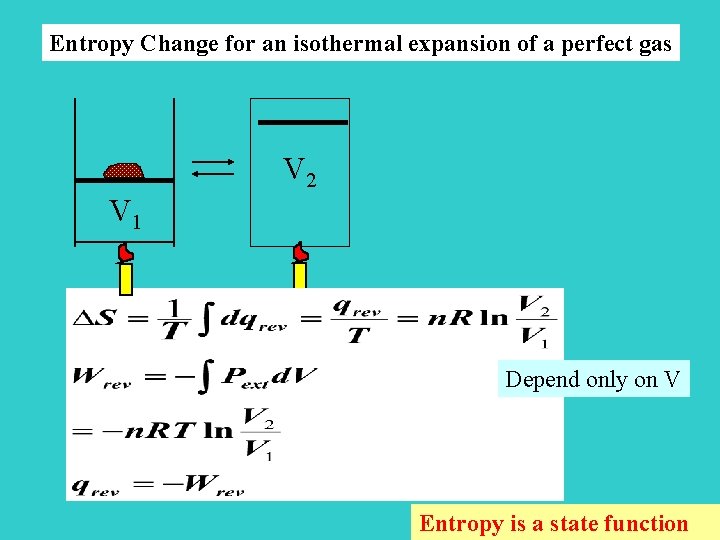
Entropy Change for an isothermal expansion of a perfect gas V 2 V 1 Depend only on V Entropy is a state function

Carnot’s Theoretical Heat Engine Heat flows from a high temperature reservoir to a low temperature body. The heat can be utilized to generate work. e. g. steam engine.

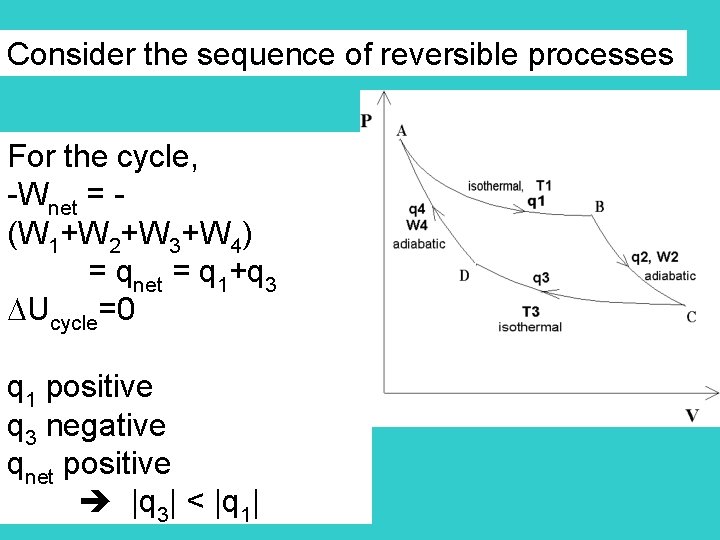
Consider the sequence of reversible processes For the cycle, -Wnet = (W 1+W 2+W 3+W 4) = qnet = q 1+q 3 Ucycle=0 q 1 positive q 3 negative qnet positive |q 3| < |q 1|

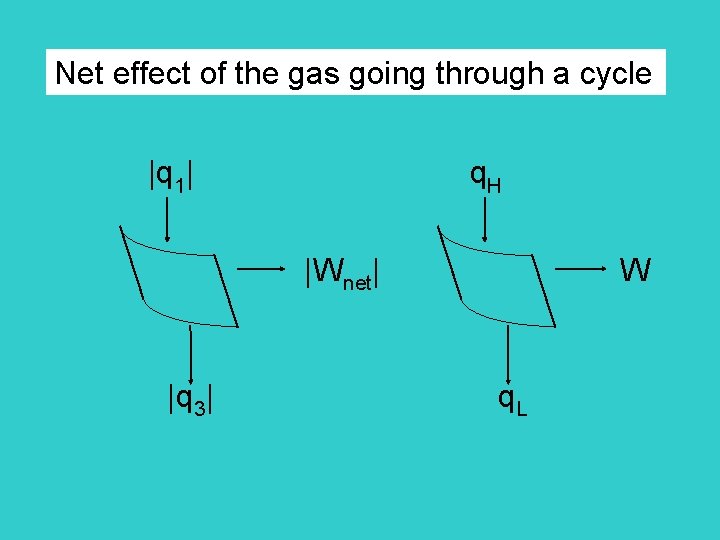
Net effect of the gas going through a cycle |q 1| q. H |Wnet| W |q 3| q. L

Efficiency of theoretical heat engine Carnot theorem: Engines operating between two temperature TH, TL have the same efficiency


limiting thermal efficiency of a heat engine In actual cases, heat engine have much lower efficient. irreversible processes, friction losses, etc. . Kelvin: It is impossible, by means of a cycle to take heat from q reservoir and convent it to work without at the same time transferring heat from a hot to cold reservoir. (We cannot have a 100% efficient heat engine)

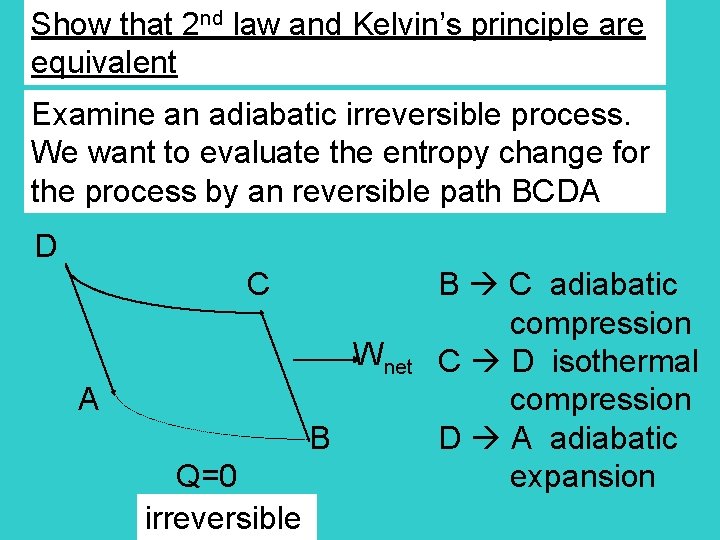
Show that 2 nd law and Kelvin’s principle are equivalent Examine an adiabatic irreversible process. We want to evaluate the entropy change for the process by an reversible path BCDA D C B C adiabatic compression Wnet C D isothermal A compression B D A adiabatic Q=0 expansion irreversible

1 st law for the cycle, U = 0 0 -(WA B + WB A) = QB A + QA B -Wnet = QB A By Kelvin’s principle, -Wnet must be negative, otherwise a 100% efficient heat engine QB A = -Wnet must be negative QB A 0

Evaluation of Entropy Changes isothermal expansion:

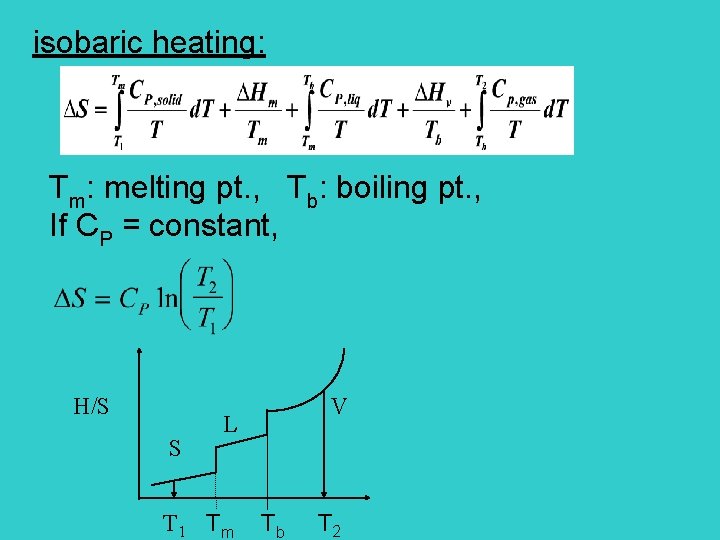
isobaric heating: Tm: melting pt. , Tb: boiling pt. , If CP = constant, H/S S L V T 1 Tm Tb T 2

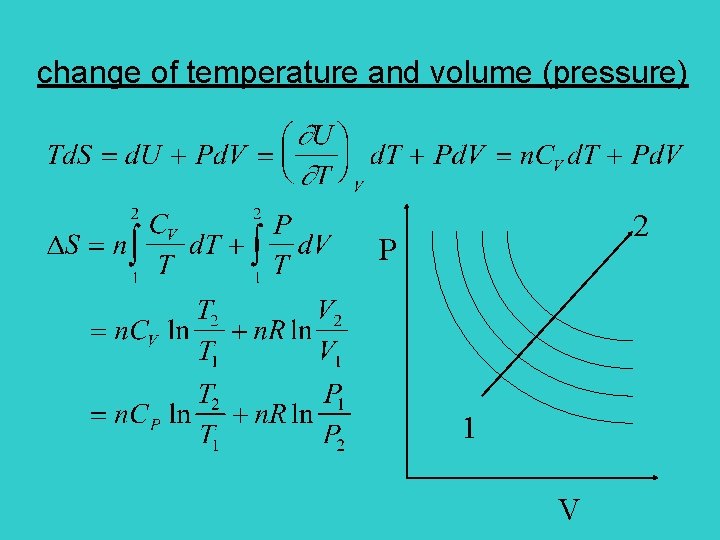
change of temperature and volume (pressure) 2 P 1 V

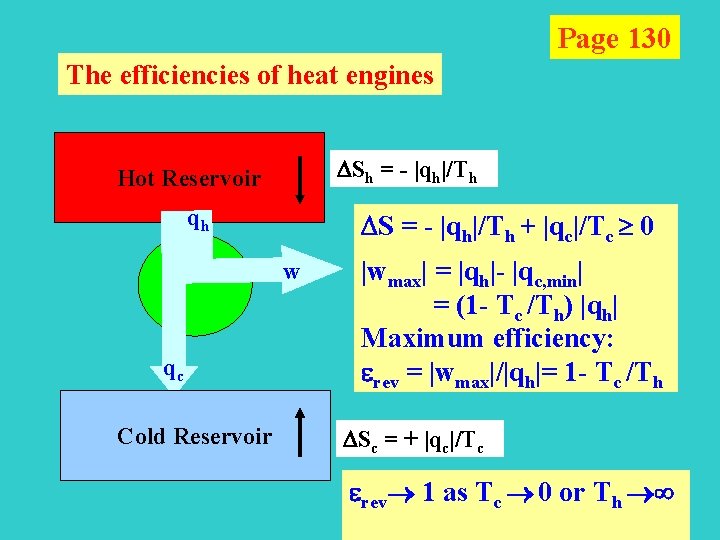
Page 142 The efficiencies of heat engines Hot Reservoir q w Engine * S = - |q|/Th < 0 not possible! contrary to the second law

Page 130 The efficiencies of heat engines Sh = - |qh|/Th Hot Reservoir qh S = - |qh|/Th + |qc|/Tc 0 w qc Cold Reservoir |wmax | = |qh|- |qc, min| = (1 - Tc /Th) |qh| Maximum efficiency: erev = |wmax|/|qh|= 1 - Tc /Th Sc = + |qc|/Tc erev 1 as Tc 0 or Th

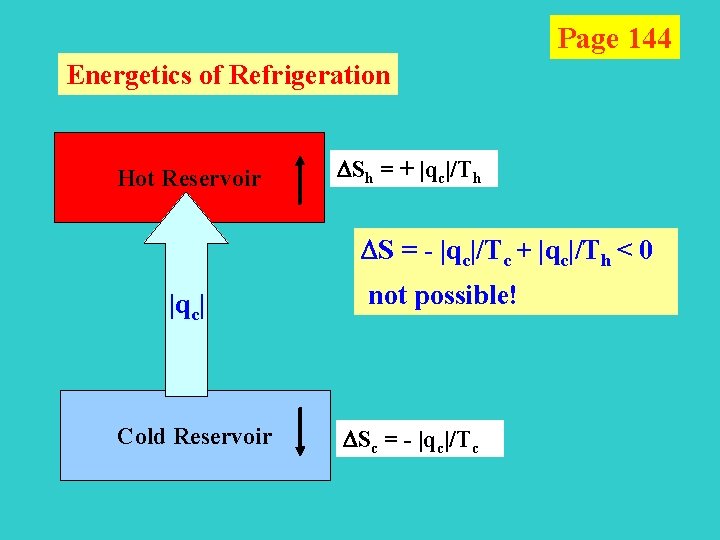
Page 144 Energetics of Refrigeration Hot Reservoir Sh = + |qc|/Th S = - |qc|/Tc + |qc|/Th < 0 |qc| Cold Reservoir not possible! Sc = - |qc|/Tc

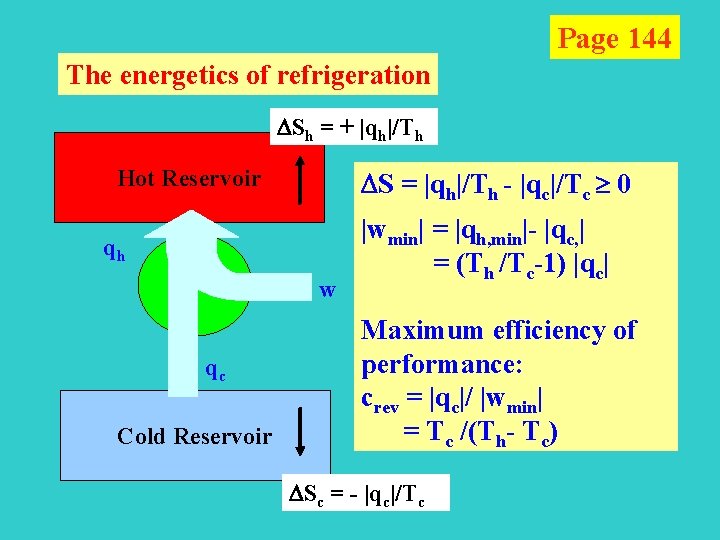
Page 144 The energetics of refrigeration Sh = + |qh|/Th Hot Reservoir qh S = |qh|/Th - |qc|/Tc 0 qh w qc Cold Reservoir |wmin| = |qh, min|- |qc, | = (Th /Tc-1) |qc| Maximum efficiency of performance: crev = |qc|/ |wmin| = Tc /(Th- Tc) Sc = - |qc|/Tc

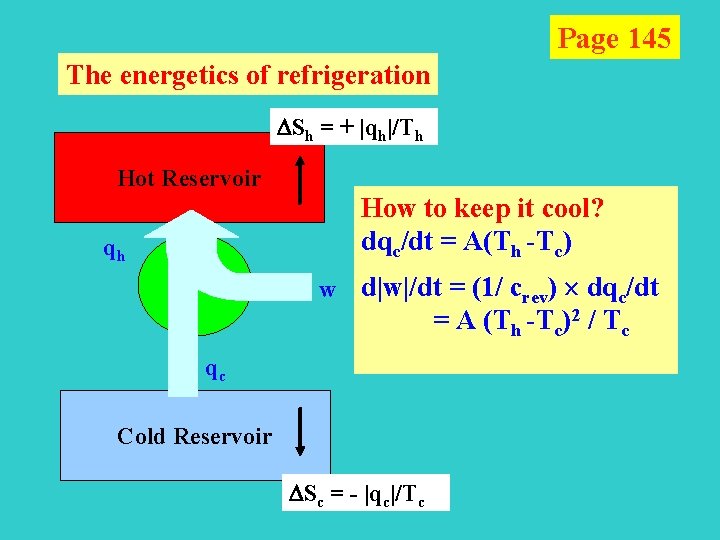
Page 145 The energetics of refrigeration Sh = + |qh|/Th Hot Reservoir qh How to keep it cool? dqc/dt = A(Th -Tc) qh w d|w|/dt = (1/ crev) dqc/dt = A (Th -Tc)2 / Tc qc Cold Reservoir Sc = - |qc|/Tc

The Nernst Theorem The entropy change accompanying any physical or chemical transformation approaches zero as the temperature approaches zero. S 0 as T 0

* Third Law of Thermodynamics Page 147 If the entropy of each element in its most state is taken as zero at the absolute zero of temperature, every substance has a positive entropy. But at 0 K, the entropy of substance may equals to 0, and does become zero in perfect crystalline solids. Implication: all perfect materials have the same entropy (S=0) at absolute zero temperature Crystalline form: complete ordered, minimum entropy

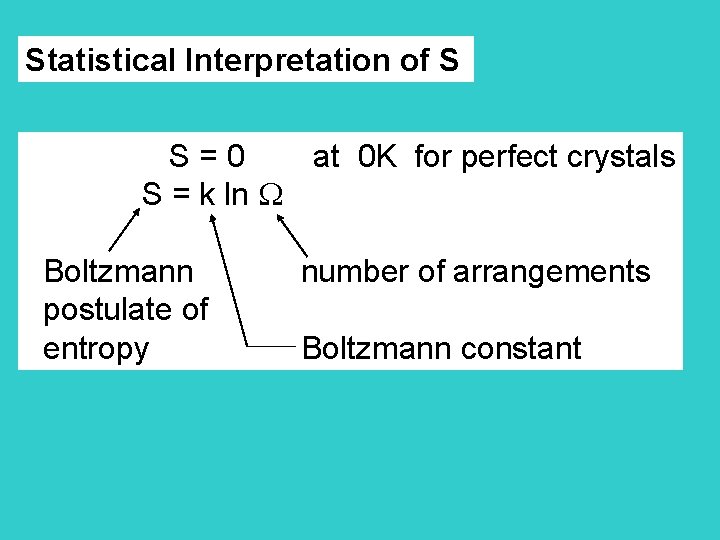
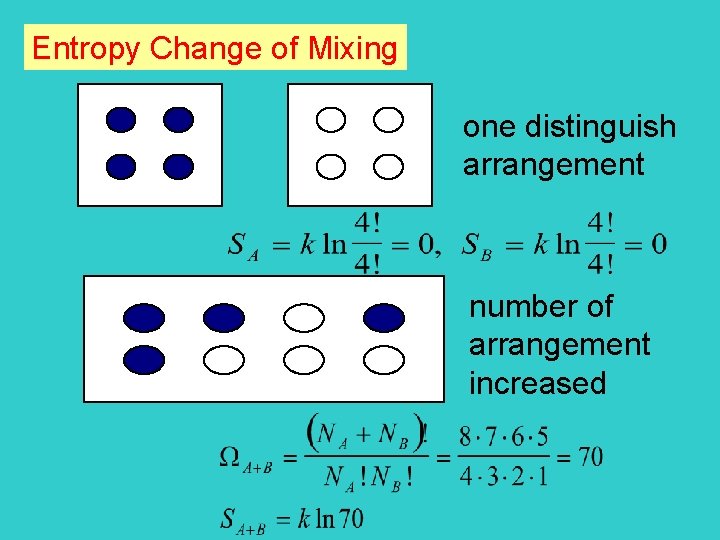
Statistical Interpretation of S S = 0 at 0 K for perfect crystals S = k ln Boltzmann number of arrangements postulate of entropy Boltzmann constant

Entropy Change of Mixing one distinguish arrangement number of arrangement increased

In general mixing NA, NB Entropy change of mixing Stirling’s approximation: ln N! N ln N + 0(N) for large N

From classical thermodynamics, isothermal reversible expansion of gases A & B

Assignment (due on 06/12/1999) 2. 4, 2. 5, 2. 37, 3. 5, 3. 23, 4. 10, 4. 29

* Extensions of 2 nd Law Page 133 Td. S dq Clausius Inequality For adiabatic process, Entropy will always attain maximum in adiabatic processes. A similar function for other processes?

* Page 149 Define Helmholtz free energy A = U - TS Thermodynamic State Function d. A = d. U - Td. S - Sd. T Substitute into Clausius Inequality * for isothermal, isochoric (constant volume) process,

* A will tend to a minimum value isothermal, isochoric process, equilibrium spontaneous If only isothermal, isothermal reversible expansion

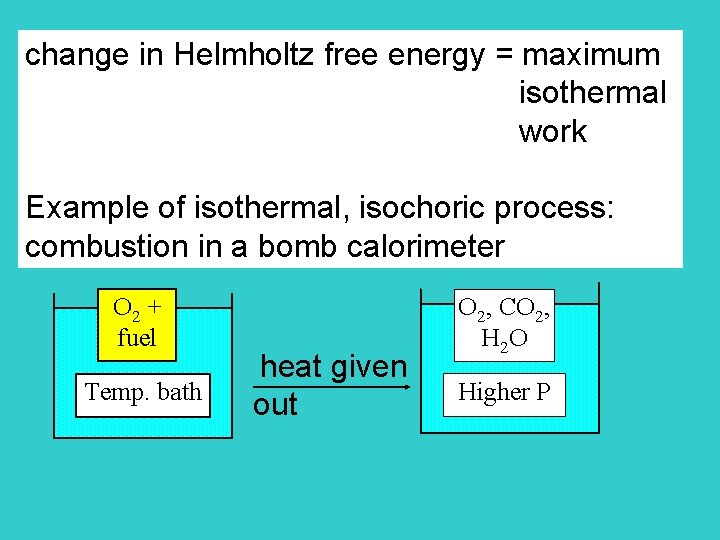
change in Helmholtz free energy = maximum isothermal work Example of isothermal, isochoric process: combustion in a bomb calorimeter O 2 + fuel Temp. bath heat given out O 2, CO 2, H 2 O Higher P

* Page 149 -155 Gibbs Free Energy Define Gibbs free energy G = H - TS Thermodynamic state function = U + PV -TS d. G = d. U +Pd. V + Vd. P -Td. S -Sd. T substitute into Clausius inequality

* constant pressure, constant temperature * G will tend to a minimum value equilibrium spontaneous change G Page 154 time More applications since most processes are isothermal, isobaric chemical reactions at constant T, P Reactants Products endothermic H is positive exothermic H is negative

H is not a criteria for spontaneity S only isolated system G G = H - T S S H G + ve - ve spontaneous dissociation of unstable compounds - ve + ve nonspontaneous + ve ? ? dissociation of a strong compound - ve ? ? recombination reaction e. g. H + H H 2 R forming unstable compounds P rxn. Co-ord.

Change of Gibbs free energy with temperature (constant pressure)

Change of Gibbs free energy with pressure (constant temperature) Ideal gas Real gas fugacity Ideal gas Real gas

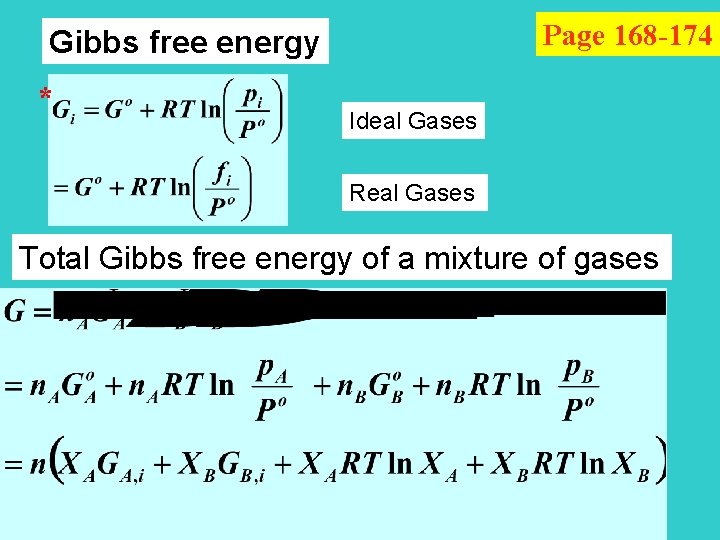
Page 168 -174 Gibbs free energy * Ideal Gases Real Gases Total Gibbs free energy of a mixture of gases

for ideal gases Chemical Equilibria a. A + b. B c. C + d. D consider G for a pass of the reaction at constant T & P G = c. GC + d. GD - a. GA - b. GB molar Gibbs free energy

fi in the unit of bar pure state fugacity 0 = SJ J J At equilibrium, G = 0 * equilibrium constant

for ideal gaseous mixture fi = pi ci = concentration n = c+d-a-b varies with total pressure

For liquids, use activity Gibbs - Helmholtz Equation Also,
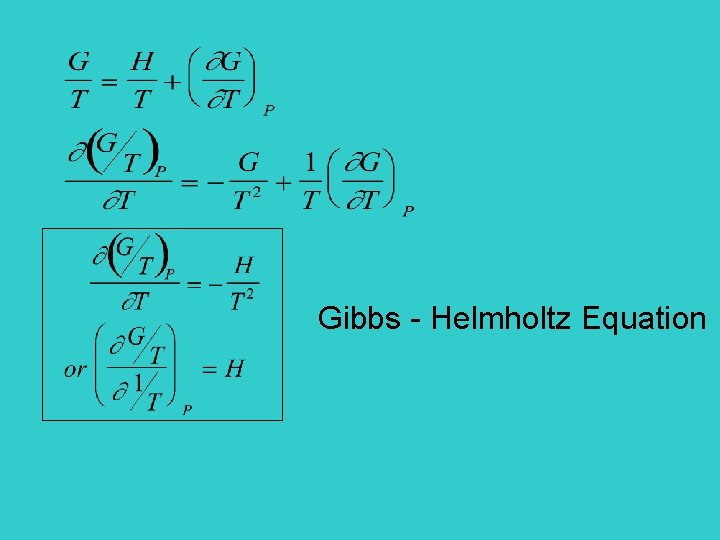
Gibbs - Helmholtz Equation

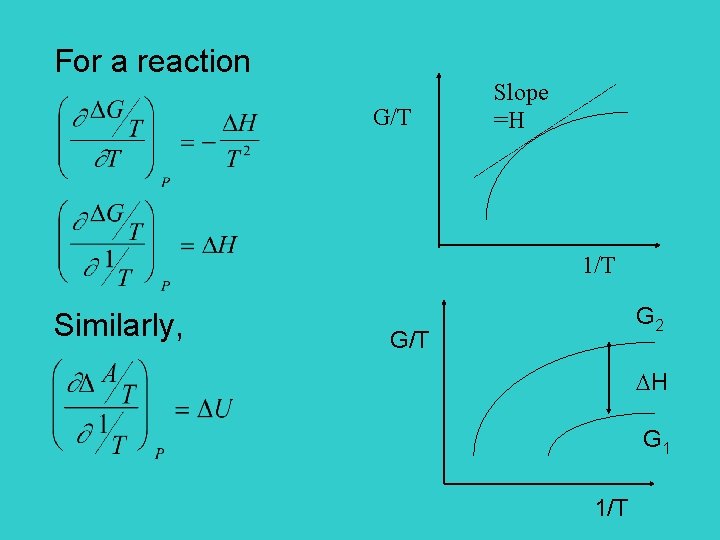
For a reaction G/T Slope =H 1/T Similarly, G 2 G/T H G 1 1/T

Change of equilibrium constant with temperature Gibbs Helmholtz equation

Van’t Hoff Equation If constant (i. e. HP -HR is constant) endothermic, H + ve, K with T exothermic, H - ve, K with T

* Relation between Thermodynamic functions d. U = Td. S-Pd. V 1 st law d. H = Td. S+Vd. P, H = U+PV d. A = -Sd. T-Pd. V, A = U-TS d. G = -Sd. T+Vd. P, G = H-TS Page 149 From multivariable differential calculus dz = M dx + N dy total differential, i. e. z depends on x & y

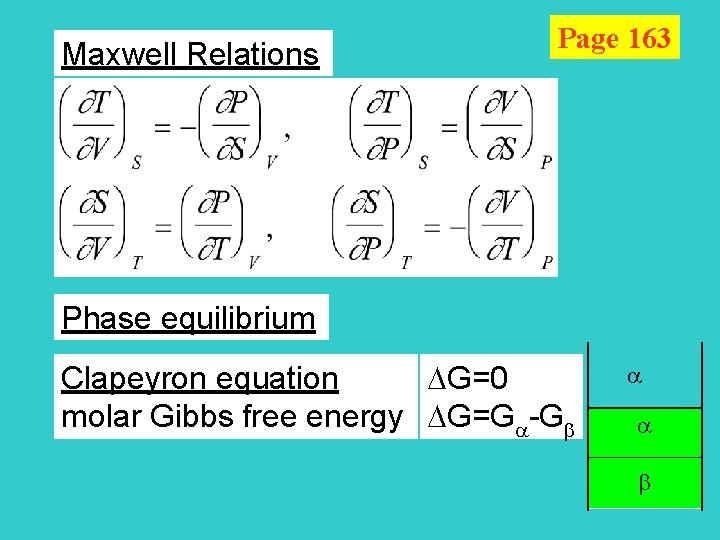
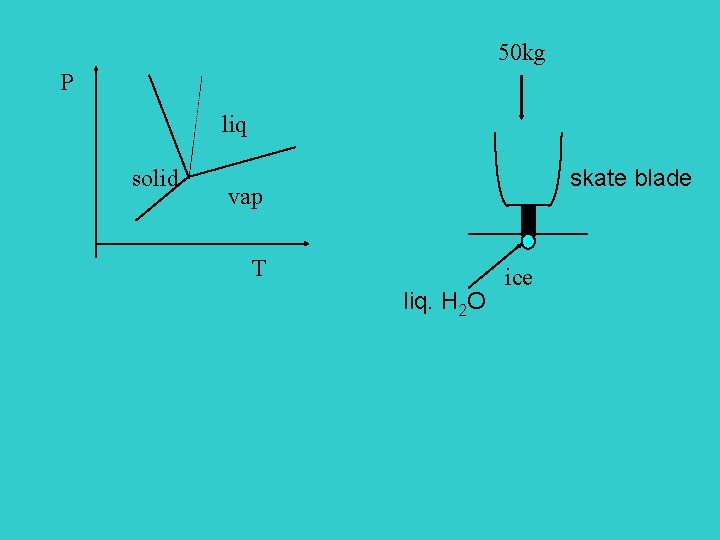
Maxwell Relations Page 163 Phase equilibrium Clapeyron equation G=0 molar Gibbs free energy G=G -G

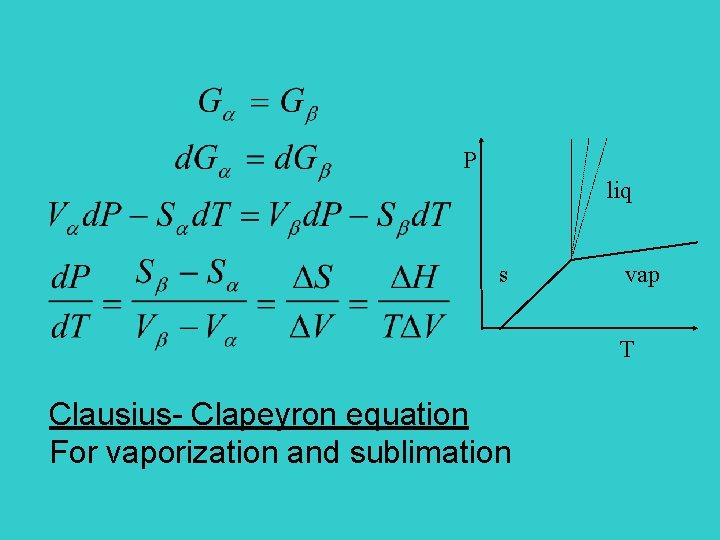
P liq s vap T Clausius- Clapeyron equation For vaporization and sublimation

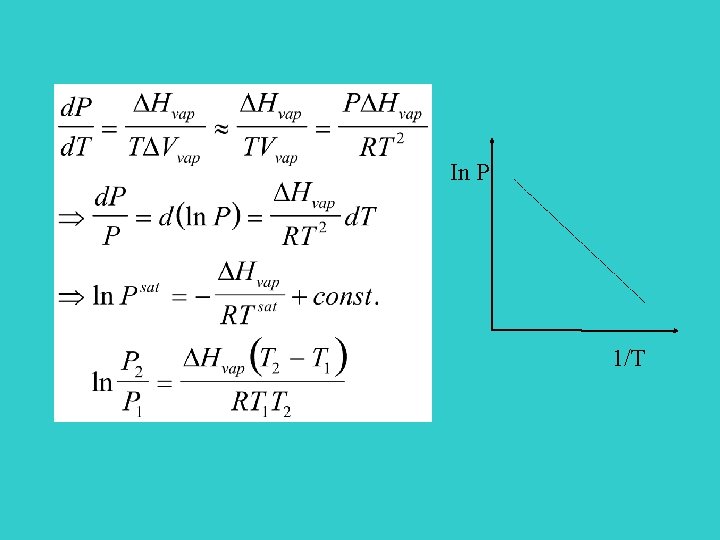
In P 1/T

Example: What is the change in the boiling point of water at 100 o. C per torr change in atmospheric pressure? Hvap = 9725 cal mol-1 Vliq = 0. 019 l mol-1 Vvap = 30. 199 l mol-1

Example: Calculate the change in pressure required to change the freezing point of water 1 o. C. At 0 o. C, the heat of the fusion of ice is 79. 7 cal g-1, the density of water is 0. 9998 g cm-3 and that of ice is 0. 9168 g

50 kg P liq solid skate blade vap T liq. H 2 O ice

Example 2. 1 A certain electric motor produced 15 k. J of energy each second as mechanical work and lost 2 k. J as heat to the surroundings. What was the change in the internal energy of the motor and its power supply each second? Example 2. 2 Calculate the work done when 50 g of iron reacts with hydrochloric acid in: (a) a closed vessel of fixed volume; (b) an open beaker at 25 o. C. Example 2. 3 The internal energy change when 1. 0 mole Ca. CO 3 in the form of calcite converts to aragonite is 0. 21 k. J. Calculate the difference between the enthalpy change and the change in internal energy.

Example 2. 4 The enthalpy change accompanying the formation of 1. 00 mole NH 3(g) from its elements at 298 K is -46. 1 k. J. Estimate the change in internal energy. Example 2. 5 Water is heated to boiling under pressure of 1. 0 atm. When an electric current of 0. 50 A from 12 -V supply is passed for 300 s through a resistance in thermal contact with it, it is found that 0. 798 g of water is vaporized. Calculate the molar internal energy and enthalpy changes at the boiling point (373. 15 K). Exercise 2. 6 At very low temperatures the heat capacity of a solid is proportional to T 3, and we can write Cv=a. T 3. What is the change in enthalpy of such a substance when it is heated from 0 to T?

Example 3. 6 A sample of argon at 1. 0 atm pressure and 25 o. C expands reversibly and adiabatically from 0. 50 L to 1. 00 L. Calculate its final temperature, the work done during the expansion, and the change in internal energy. The molar heat capacity of argon at constant volume is 12. 48 JK-1 mol-1. Example 4. 1 Calculate the entropy change in the surroundings when 1. 00 mol H 2 O(l) is formed from its elements under standard conditions at 298. 15 K. Example 4. 4 Calculate the entropy change when argon at 25 o. C and 1. 00 atm in a container of volume 500 cm 3 is allowed to expand to 1000 cm 3 and is simultaneously heated to 100 o. C.

Example 5. 4 The pressure deep inside the Earth is probably greater than 3× 103 kbar, and the temperature is around 4× 103 o. C. Estimate the change in G on going from crust to core for a process in which V=1. 0 cm 3 mol-1 and S = 2. 1 JK-1 mol-1. Example 5. 5 Calculate the change in molar Gibbs energy when water vaporizes at 1 bar and 25 o. C. Note that the molar Gibbs energies of formation are -237. 13 and -228. 57 k. J mol-1 for water and its vapor, respectively. Example 5. 6 Suppose that the attractive interactions between gas particles can be neglected and find an expression for the fugacity of a van der Waals gas in terms of the pressure.