Gases Ideal Gases Ideal gases are imaginary gases





























- Slides: 30

Gases

Ideal Gases Ideal gases are imaginary gases that perfectly fit all of the assumptions of the kinetic molecular theory. Ø Gases consist of tiny particles that are far apart relative to their size. Ø Collisions between gas particles and between particles and the walls of the container are elastic collisions Ø No kinetic energy is lost in elastic collisions

Ideal Gases (continued) q Gas particles are in constant, rapid motion. They therefore possess kinetic energy, the energy of motion q There are no forces of attraction between gas particles q The average kinetic energy of gas particles depends on temperature, not on the identity of the particle.

The Nature of Gases q Gases expand to fill their containers q Gases are fluid – they flow q Gases have low density q 1/1000 the density of the equivalent liquid or solid q Gases are compressible q Gases effuse and diffuse

Pressure q Is caused by the collisions of molecules with the walls of a container q is equal to force/unit area q SI units = Newton/meter 2 = 1 Pascal (Pa) q 1 atmosphere = 101, 325 Pa q 1 atmosphere = 1 atm = 760 mm Hg = 760 torr

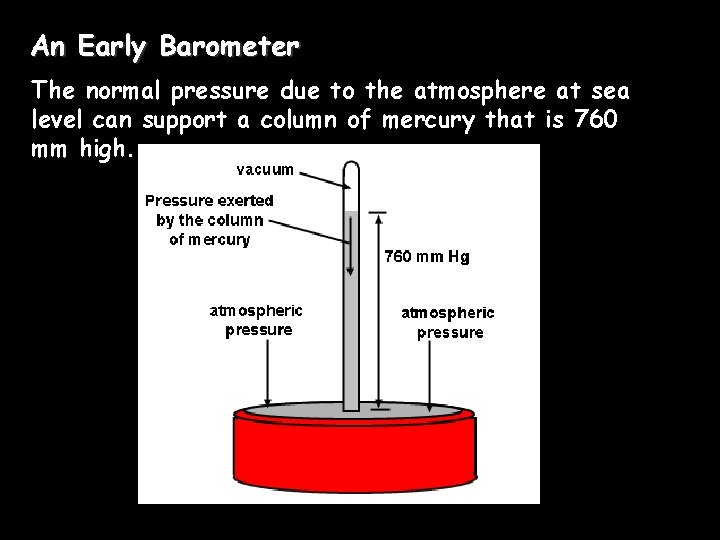
Measuring Pressure The first device for measuring atmospheric pressure was developed by Evangelista Torricelli during the 17 th century. The device was called a “barometer” Baro = weight Meter = measure

An Early Barometer The normal pressure due to the atmosphere at sea level can support a column of mercury that is 760 mm high.

Standard Temperature and Pressure “STP” • • • P = 1 atmosphere, 760 torr T = 0 C, 273 Kelvins The molar volume of an ideal gas is 22. 42 liters at STP

Converting Celsius to Kelvin Gas law problems involving temperature require that the temperature be in KELVINS! Kelvins = C + 273 °C = Kelvins - 273

The Combined Gas Law The combined gas law expresses the relationship between pressure, volume and temperature of a fixed amount of gas. Boyle’s law, Gay-Lussac’s law, and Charles’ law are all derived from this by holding a variable constant.

Boyle’s Law Pressure is inversely proportional to volume when temperature is held constant.

Charles’s Law • The volume of a gas is directly proportional to temperature, and extrapolates to zero at zero Kelvin. (P = constant)

Gay Lussac’s Law The pressure and temperature of a gas are directly related, provided that the volume remains constant.

Avogadro’s Law v For a gas at constant temperature and pressure, the volume is directly proportional to the number of moles of gas (at low pressures). V = an a = proportionality constant V = volume of the gas n = number of moles of gas

Ideal Gas Law PV = n. RT v P = pressure in atm v V = volume in liters v n = moles v R = proportionality constant v= 0. 08206 L atm/ mol·K v T = temperature in Kelvins Holds closely at P < 1 atm

Standard Molar Volume Equal volumes of all gases at the same temperature and pressure contain the same number of molecules. - Amedeo Avogadro

Gas Density … so at STP…

Density and the Ideal Gas Law Combining the formula for density with the Ideal Gas law, substituting and rearranging algebraically: M = Molar Mass P = Pressure R = Gas Constant T = Temperature in Kelvins

Gas Stoichiometry #1 If reactants and products are at the same conditions of temperature and pressure, then mole ratios of gases are also volume ratios. 3 H 2(g) + N 2(g) 2 NH 3(g) 3 moles H 2 + 1 mole N 2 2 moles NH 3 3 liters H 2 + 1 liter N 2 2 liters NH 3

Gas Stoichiometry #2 How many liters of ammonia can be produced when 12 liters of hydrogen react with an excess of nitrogen? 3 H 2(g) + 12 L H 2 N 2(g) 2 L NH 3 3 L H 2 2 NH 3(g) = 8. 0 L NH 3

Gas Stoichiometry #3 How many liters of oxygen gas, at STP, can be collected from the complete decomposition of 50. 0 grams of potassium chlorate? 2 KCl. O 3(s) 2 KCl(s) + 3 O 2(g) 50. 0 g KCl. O 3 1 mol KCl. O 3 122. 55 g KCl. O 3 3 mol O 2 22. 4 L O 2 2 mol KCl. O 3 1 mol O 2 = 13. 7 L O 2

Gas Stoichiometry #4 How many liters of oxygen gas, at 37. 0 C and 0. 930 atmospheres, can be collected from the complete decomposition of 50. 0 grams of potassium chlorate? 2 KCl. O 3(s) 2 KCl(s) + 3 O 2(g) 50. 0 g KCl. O 3 1 mol KCl. O 3 122. 55 g KCl. O 3 3 mol O 2 2 mol KCl. O 3 = “n” 0. 612 mol O 2 = 16. 7 L

Dalton’s Law of Partial Pressures For a mixture of gases in a container, PTotal = P 1 + P 2 + P 3 +. . . This is particularly useful in calculating the pressure of gases collected over water.

Kinetic Energy of Gas Particles At the same conditions of temperature, all gases have the same average kinetic energy.

The Meaning of Temperature q Kelvin temperature is an index of the random motions of gas particles (higher T means greater motion. )

Kinetic Molecular Theory q Particles of matter are ALWAYS in motion q Volume of individual particles is zero. q Collisions of particles with container walls cause pressure exerted by gas. q Particles exert no forces on each other. q Average kinetic energy µ Kelvin temperature of a gas.

Diffusion: describes the mixing of gases. The rate of diffusion is the rate of gas mixing.

Effusion: describes the passage of gas into an evacuated chamber.

Graham’s Law Rates of Effusion and Diffusion Effusion: Diffusion:

Real Gases Must correct ideal gas behavior when at high pressure (smaller volume) and low temperature (attractive forces become important). corrected pressure Pideal corrected volume Videal
 Insidan region jh
Insidan region jh An ideal gas is an imaginary gas
An ideal gas is an imaginary gas A rope attaches a tire to an overhanging tree limb
A rope attaches a tire to an overhanging tree limb Kinetic molecular theory
Kinetic molecular theory First law of thermodynamics
First law of thermodynamics Characteristics of ideal gases
Characteristics of ideal gases Characteristics of ideal gas
Characteristics of ideal gas Are ideal gases compressible
Are ideal gases compressible Laplace transform with complex roots
Laplace transform with complex roots How to graph polynomials with imaginary roots
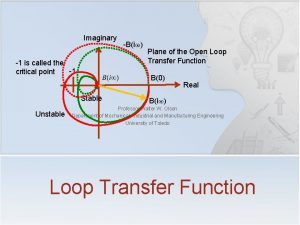
How to graph polynomials with imaginary roots Can critical point be imaginary
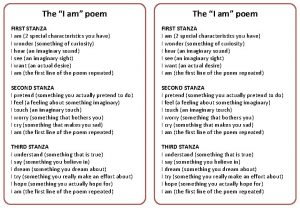
Can critical point be imaginary What is a stanza in a poem
What is a stanza in a poem Imaginary surfaces
Imaginary surfaces Spleen percussion
Spleen percussion Multiplying two complex numbers
Multiplying two complex numbers Imaginary learning
Imaginary learning Missouri compromise
Missouri compromise Imaginary feelings i am poem
Imaginary feelings i am poem The imaginary voice assumed by the writer of a poem.
The imaginary voice assumed by the writer of a poem. Emphasis in photography
Emphasis in photography An imaginary gas that conforms perfectly
An imaginary gas that conforms perfectly The imaginary voice assumed by the writer of a poem.
The imaginary voice assumed by the writer of a poem. Imaginary roots
Imaginary roots The curving of these planetary winds is the result of
The curving of these planetary winds is the result of Negative square root
Negative square root How to add and subtract imaginary numbers
How to add and subtract imaginary numbers Imaginary i
Imaginary i Spinal cavity
Spinal cavity Phase of complex number
Phase of complex number How to draw multiview drawings
How to draw multiview drawings The elixir of life by cv raman
The elixir of life by cv raman