Gases III Ideal Gas Law A Ideal Gas

Gases III. Ideal Gas Law

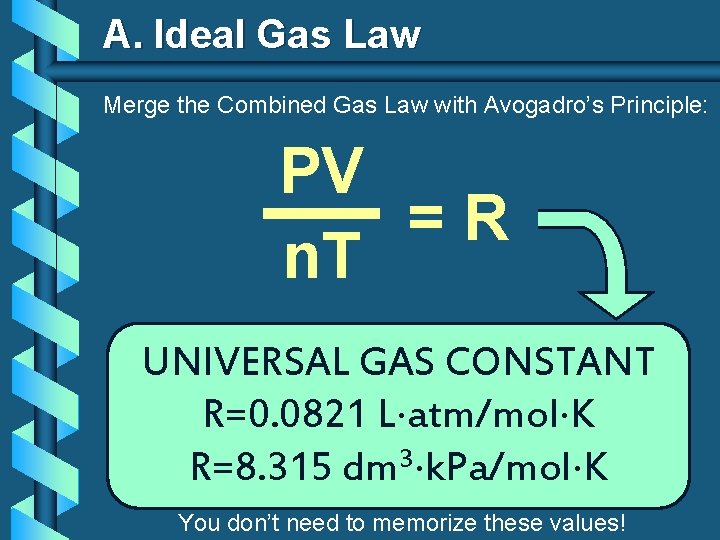
A. Ideal Gas Law Merge the Combined Gas Law with Avogadro’s Principle: PV V k =R n. T T n UNIVERSAL GAS CONSTANT R=0. 0821 L atm/mol K 3 R=8. 315 dm k. Pa/mol K You don’t need to memorize these values!

A. Ideal Gas Law PV=n. RT UNIVERSAL GAS CONSTANT R=0. 0821 L atm/mol K 3 R=8. 315 dm k. Pa/mol K You don’t need to memorize these values!

C. Ideal Gas Law Problems b Calculate the pressure in atmospheres of 0. 412 mol of He at 16°C & occupying 3. 25 L. GIVEN: WORK: P = ? atm PV = n. RT n = 0. 412 mol P(3. 25)=(0. 412)(0. 0821)(289) mol L atm/mol K T = 16°C = 289 K K L V = 3. 25 L P = 3. 01 atm R= 0. 0821 L atm/mol K

C. Ideal Gas Law Problems b Find the volume of 85 g of O 2 at 25°C and 104. 5 k. Pa. GIVEN: WORK: V=? 85 g 1 mol = 2. 7 mol n = 85 g = 2. 7 mol 32. 00 g T = 25°C = 298 K PV = n. RT P = 104. 5 k. Pa (104. 5)V=(2. 7) (8. 315) (298) k. Pa mol dm 3 k. Pa/mol K R = 8. 315 V = 64 dm 3 k. Pa/mol K

A. Gas Stoichiometry Liters of a Gas: • STP - use 22. 4 L/mol • Non-STP - use ideal gas law b Moles b Non-STP • Given liters of gas? Ø start with ideal gas law • Looking for liters of gas? Ø start with stoichiometry conv. C. Johannesson

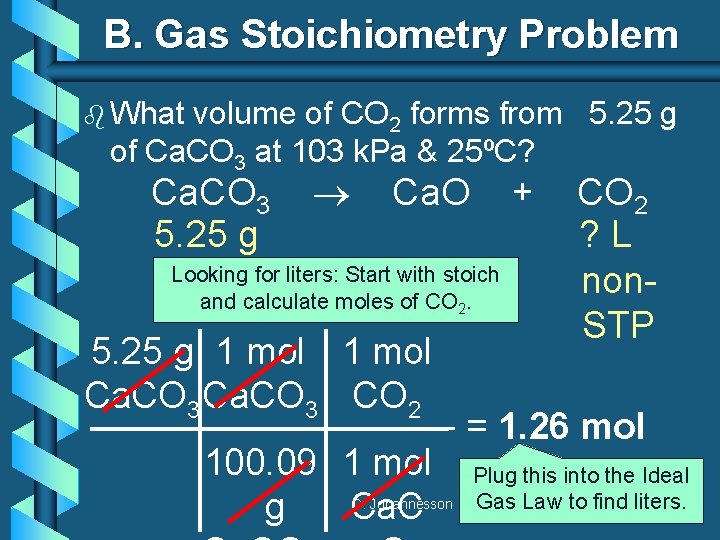
B. Gas Stoichiometry Problem b What volume of CO 2 forms from 5. 25 g of Ca. CO 3 at 103 k. Pa & 25ºC? Ca. CO 3 5. 25 g Ca. O Looking for liters: Start with stoich and calculate moles of CO 2. 5. 25 g 1 mol Ca. CO 3 CO 2 + CO 2 ? L non. STP = 1. 26 mol 100. 09 1 mol Plug. CO this into 2 the Ideal g Ca. C Gas Law to find liters. C. Johannesson

B. Gas Stoichiometry Problem b What volume of CO 2 forms from 5. 25 g of Ca. CO 3 at 103 k. Pa & 25ºC? GIVEN: WORK: P = 103 k. Pa V=? n = 1. 26 mol T = 25°C = 298 K R = 8. 315 PV = n. RT (103 k. Pa)V =(1 mol)(8. 315 dm 3 k. Pa/mol K)( 298 K) dm 3 k. Pa/mol K V = 1. 26 dm 3 CO 2 C. Johannesson

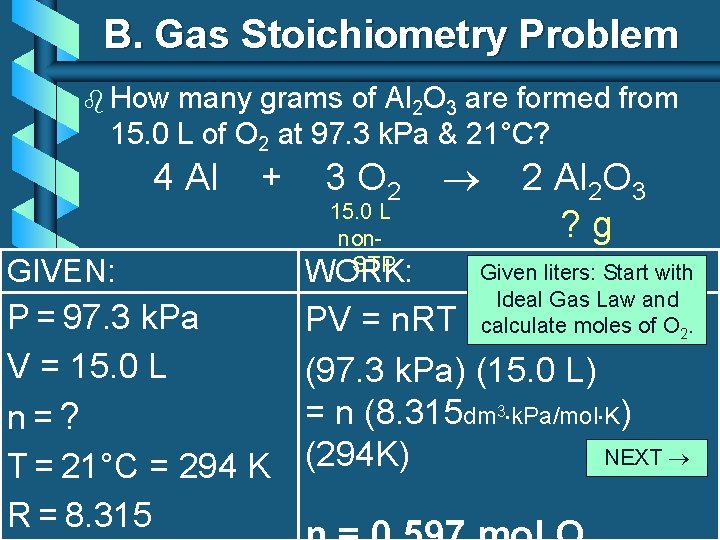
B. Gas Stoichiometry Problem b How many grams of Al 2 O 3 are formed from 15. 0 L of O 2 at 97. 3 k. Pa & 21°C? 4 Al + GIVEN: P = 97. 3 k. Pa V = 15. 0 L n=? T = 21°C = 294 K R = 8. 315 3 O 2 15. 0 L non. STP WORK: 2 Al 2 O 3 ? g Given liters: Start with Ideal Gas Law and calculate moles of O 2. PV = n. RT (97. 3 k. Pa) (15. 0 L) = n (8. 315 dm 3 k. Pa/mol K) NEXT (294 K) C. Johannesson

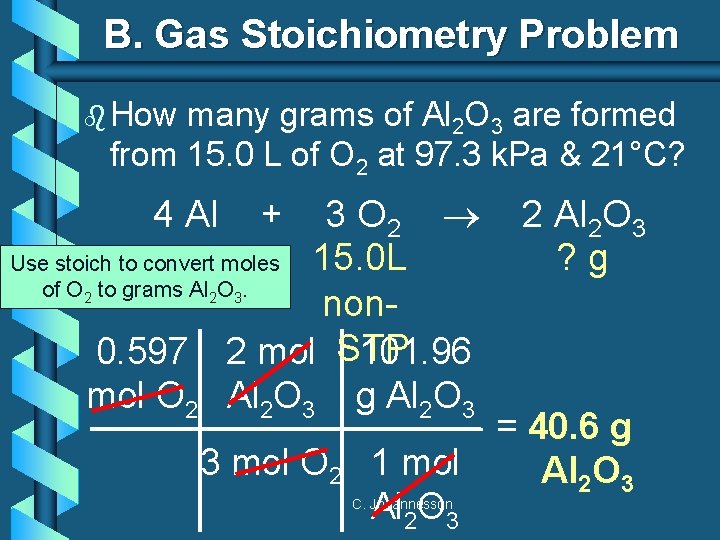
B. Gas Stoichiometry Problem b How many grams of Al 2 O 3 are formed from 15. 0 L of O 2 at 97. 3 k. Pa & 21°C? 3 O 2 Use stoich to convert moles 15. 0 L of O to grams Al O. non 0. 597 2 mol STP 101. 96 mol O 2 Al 2 O 3 g Al 2 O 3 4 Al 2 2 + 2 Al 2 O 3 ? g 3 3 mol O 2 = 40. 6 g 1 mol Al 2 O 3 C. Johannesson

C. Dalton’s Law b The total pressure of a mixture of gases equals the sum of the partial pressures of the individual gases. Ptotal = P 1 + P 2 +. . . When a H 2 gas is collected by water displacement, the gas in the collection bottle is actually a mixture of H 2 C. Johannesson and water vapor.

C. Dalton’s Law b Hydrogen gas is collected over water at 22. 5°C. Find the pressure of the dry gas if the atmospheric pressure is 94. 4 k. Pa. The total pressure in the collection bottle is equal to atmospheric pressure and is a mixture of H 2 and water vapor. GIVEN: PH 2 = ? Ptotal = 94. 4 k. Pa PH 2 O = 2. 72 k. Pa Look up water-vapor pressure on p. 899 for 22. 5°C. WORK: Ptotal = PH 2 + PH 2 O 94. 4 k. Pa = PH 2 + 2. 72 k. Pa PH 2 = 91. 7 k. Pa Sig Figs: Round to least number C. Johannesson of decimal places.

C. Dalton’s Law b A gas is collected over water at a temp of 35. 0°C when the barometric pressure is 742. 0 torr. What is the partial pressure of the dry gas? The total pressure in the collection bottle is equal to barometric pressure and is a mixture of the “gas” and water vapor. GIVEN: Pgas = ? Ptotal = 742. 0 torr PH 2 O = 42. 2 torr Look up water-vapor pressure on p. 899 for 35. 0°C. WORK: Ptotal = Pgas + PH 2 O 742. 0 torr = PH 2 + 42. 2 torr Pgas = 699. 8 torr Sig Figs: Round to least number C. Johannesson of decimal places.