Kinetic Theory The state of matter is determined

Kinetic Theory • The state of matter is determined by the motion of its particles.

Kinetic Theory and Gases • Gases consist of tiny particles that are in constant motion • Collisions between particles of a gas and other objects are elastic-there is no loss of kinetic energy • Average kinetic energy of particles of a gas is directly proportional to the temp. of the gas

Nature of Gases • • • Gases have no definite shape or volume Gases have low density Gases can be compressed Gases are considered fluids Gases are capable of diffusion-they can spread out with the absence of circulating currents

Ideal Gas • An imaginary gas that conforms perfectly to all of the assumptions of kinetic theory

Real Gas • A gas that does not obey all of the assumptions of kinetic theory • Gases will deviate from ideal gas behavior under conditions of high temp. and pressure.

Pressure • • The force per unit area on a surface Gas molecules exert pressure on every surface with which they collide-the pressure exerted depends on: 1. Number of molecules present 2. Temp. 3. Volume of container

What is normal atmospheric pressure? • At sea level, the normal atmospheric pressure is 1 atmosphere (atm) • 1 atm = 760 mm Hg • 1 atm = 760 torr • 1 atm = 101. 3 k. Pa

Standard Temperature and Pressure • (STP) is defined as: 1 atm and 0 degrees Celsius

Boyle’s Law • Relates changes in pressure and volume assuming constant temp. and molecules of gas. • States that pressure and volume are inversely proportional P 1 V 1=P 2 V 2

Charles’ Law • Relates changes in volume and temp. assuming constant pressure and molecules of gas. • States that volume and temp. are directly proportional. V 1 = V 2 T 1 T 2 Varies directly with the Kelvin scale so all temps must be in Kelvin Remember… K= C + 273

Gay-Lussac’s Law • Relates changes in pressure and temperature assuming constant volume and molecules of gas. • Temps must be in Kelvin P 1 = P 2 T 1 = T 2

Combined Gas Law • Relates changes in pressure, temp. and volume assuming the amount of gas is held constant. P 1 V 1 = P 2 V 2 T 1 T 2

Dalton’s Law of Partial Pressure • The total pressure of a mixture of gases is equal to the sum of the partial pressures of the component gases. • Partial pressure- the pressure of an individual gas in a mixture of gases Pt = P 1 + P 2 + P 3 …… Where Pt = total pressure and P 1, P 2, etc. = partial pressures of individual gases

Partial Pressures are used to: • Calculate water vapor pressure when a gas is collected over water. • Because water molecules at a liquid surface always evaporate, gases collected over water are not pure…. they are always mixed with water vapor…. so Dalton’s Law is used to calculate the partial pressure of the gas.

Example Problems: • Look at what information is given to decide which gas law must be used. • Check to make sure that units are the same on both sides of the equation and that all temps. are in Kelvin

1. A sample of nitrogen occupies a volume of 250 m. L at 25 C. What volume will it occupy at 95 C? 2. A sample of carbon dioxide gas occupies a volume of 3. 50 L at 125 k. Pa. What pressure would the gas exert if the volume was decreased to 2. 00 L? 3. A helium filled balloon has a volume of 50 L at 25 C and 820 mm. Hg. What volume will it occupy at 650 mm Hg and 10 C?

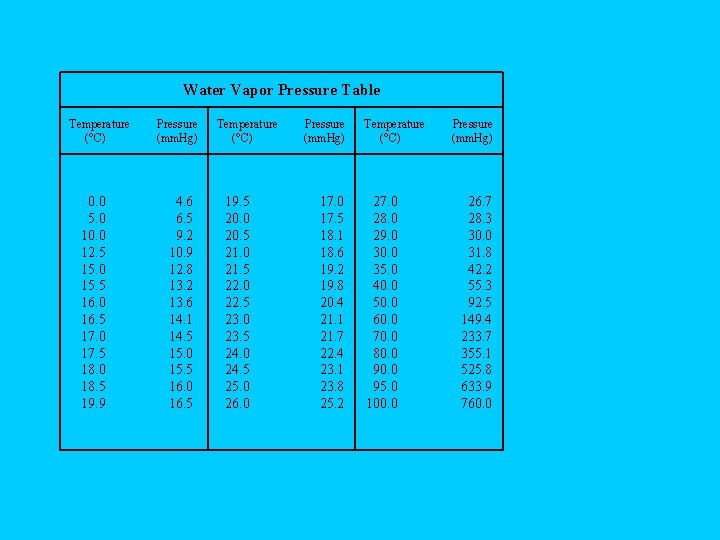
• Oxygen from the decomposition of potassium chlorate was collected over water. The barometric pressure and the temp. during the experiment were 731 mm Hg and 20 C. What was the partial pressure of oxygen collected? (Use the water vapor pressure on the back of your periodic table to solve. )

Water Vapor Pressure Table Temperature (°C) 0. 0 5. 0 10. 0 12. 5 15. 0 15. 5 16. 0 16. 5 17. 0 17. 5 18. 0 18. 5 19. 9 Pressure (mm. Hg) 4. 6 6. 5 9. 2 10. 9 12. 8 13. 2 13. 6 14. 1 14. 5 15. 0 15. 5 16. 0 16. 5 Temperature (°C) 19. 5 20. 0 20. 5 21. 0 21. 5 22. 0 22. 5 23. 0 23. 5 24. 0 24. 5 25. 0 26. 0 Pressure (mm. Hg) 17. 0 17. 5 18. 1 18. 6 19. 2 19. 8 20. 4 21. 1 21. 7 22. 4 23. 1 23. 8 25. 2 Temperature (°C) 27. 0 28. 0 29. 0 30. 0 35. 0 40. 0 50. 0 60. 0 70. 0 80. 0 95. 0 100. 0 Pressure (mm. Hg) 26. 7 28. 3 30. 0 31. 8 42. 2 55. 3 92. 5 149. 4 233. 7 355. 1 525. 8 633. 9 760. 0

• A sample of gas was collected over water at 740 mm Hg and 23 C. The collecting tube is left in place, and the volume is not measured until the next day when the dry gas was found to have a pressure of 745 mm Hg and a temp. of 20 C, at which time the volume is found to be 15. 3 m. L. What is the original volume?

Ideal Gas Law • Expresses a relationship between pressure, volume, temp. and moles of gas PV= n. RT (where P= pressure, V= volume, n= moles, R= ideal gas constant, and T= temp)

Ideal Gas Constant • The constant’ value depends on the units chosen for pressure, volume, and temp. • If 1 mole of a gas occupies 22. 4 L at STP (0 degrees C and 1 atm) and these values are substituted into the ideal gas law, the value for R can be calculated: R = PV = (1 atm)( 22. 4 L) = 0. 0821 L. atm n. T (1 mol) (273 K) mol. K Since R has units of L, atm, mol, and K, all pressure, volumes, temps. , and amounts must also be expressed in these units.

Examples: • What is the pressure in atm exerted by 0. 50 mol sample of nitrogen in a 10 L container at 298 K? • What is the volume in liters occupied by 0. 25 mol of oxygen at 20 degrees C and 740 mm Hg?

More Examples: • At 28 C and 0. 974 atm, 1. 00 L of a gas has a mass of 5. 16 g. What is the molar mass of the gas? (Hint. . Remember that molar mass is in units of g/mol)

Stoichiometry of Gases • Remember. . 1 mol of any gas at STP will occupy 22. 4 L -this is called molar volume

When solving stoichiometry problems involving gases the following will be used: • • Given Unknown Mol ratio –compares given and unknown Molar mass-if given is in grams or unknown is asked for in grams • Molar volume- ONLY IF AT STP-used to convert moles to liters or liters to moles

Example: C 3 H 8 (g) + 5 O 2 (g) 3 CO 2 (g) + 4 H 2 O (g) a) What volume in liters of oxygen would be required for the complete combustion of 0. 350 L of propane? b) What volume of CO 2 will be produced?

• How many grams of calcium carbonate must be decomposed to produce 5 L of carbon dioxide at STP? Ca. CO 3 (s) Ca. O (s) + CO 2 (g)

Gas Stoichiometry #1 1. 2 Fe + 3 H 2 SO 4 3 H 2 + Fe 2(SO 4)3 5. SO 2 + H 2 O H 2 SO 3 8. 2 KOH + (NH 4)2 SO 4 K 2 SO 4 + 2 NH 3 + 2 H 2 O

Gas Stoichiometry #2 1. 3. 4. 5. 6. 2 Al + 3 H 2 SO 4 Al 2(SO 4)3 + 3 H 2 C 2 H 5 OH + 3 O 2 2 CO 2 + 3 H 2 O SO 2 + H 2 O H 2 SO 3 CH 4 + 2 O 2 CO 2 + 2 H 2 O 4 C 3 H 5(NO 3)3 + O 2 12 CO 2 + 6 N 2 + 2 O 2 + 10 H 2 O 7. Fe 2 O 3 + 3 CO 2 Fe + 3 CO 2 8. Cu + 2 H 2 SO 4 Cu. SO 4 +SO 2 + 2 H 2 O

• WO 3 (s) +3 H 2 (g) W (s) + 3 H 2 O (l) How many liters of hydrogen at 35 C and 745 mm Hg are needed to react completely with 875 g of tungsten oxide? (Because we are not at STP, 1 mol of the gas will no longer occupy 22. 4 L. . so molar volume can not be used but we need a way to convert mol into liters to use in stoichiometry…. we will have to use the Ideal Gas Law)

To decide which to use first: • Write down the given and unknown • Write down the variables for the gas law, using in pressures, volumes, temps. , that are given in the problem. • If there is enough info to solve the gas law 1 st, do so. You will be solving for moles of whatever the volume amount is for.

• If there is not enough info to solve the gas law 1 st, use the given to find the moles of what you are trying to find the volume of…plug moles back into the gas law and solve for volume.

2 Na (s) + Cl 2 (g) 2 Na. Cl (s) How many grams of Na should be used to react with 3. 54 L of chlorine at 38 C and 1. 63 atm?