http zoi utia cas czmomentinvariants The slides accompanying









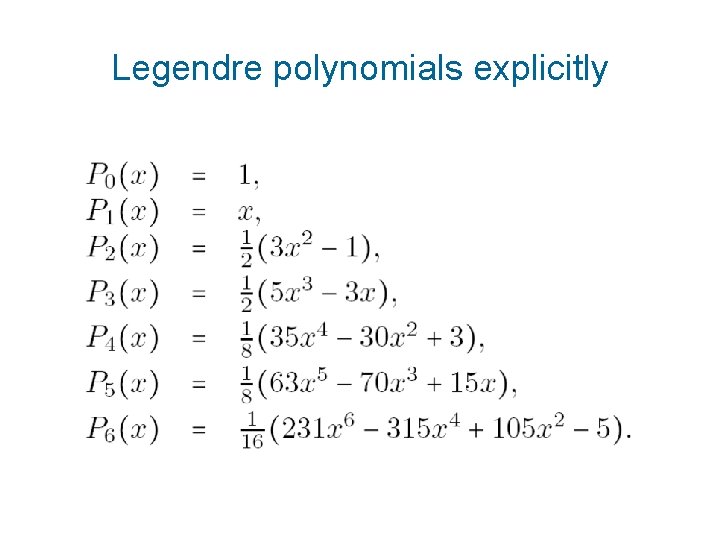




































- Slides: 65

http: //zoi. utia. cas. cz/moment_invariants The slides accompanying the book J. Flusser, T. Suk, and B. Zitová Moments and Moment Invariants in Pattern Recognition

Copyright notice The slides can be used freely for non-profit education provided that the source is appropriately cited. Please report any usage on a regular basis (namely in university courses) to the authors. For commercial usage ask the authors for permission. The slides containing animations are not appropriate to print. © Jan Flusser, Tomas Suk, and Barbara Zitová, 2009

Contents 1. Introduction to moments 2. Invariants to translation, rotation and scaling 3. Affine moment invariants 4. Implicit invariants to elastic transformations 5. Invariants to convolution 6. Orthogonal moments 7. Algorithms for moment computation 8. Applications 9. Conclusion

Chapter 6

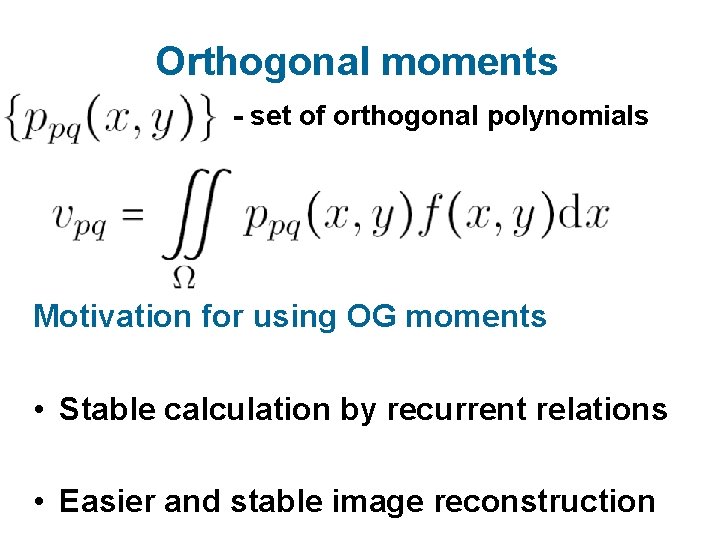
Orthogonal moments - set of orthogonal polynomials Motivation for using OG moments • Stable calculation by recurrent relations • Easier and stable image reconstruction

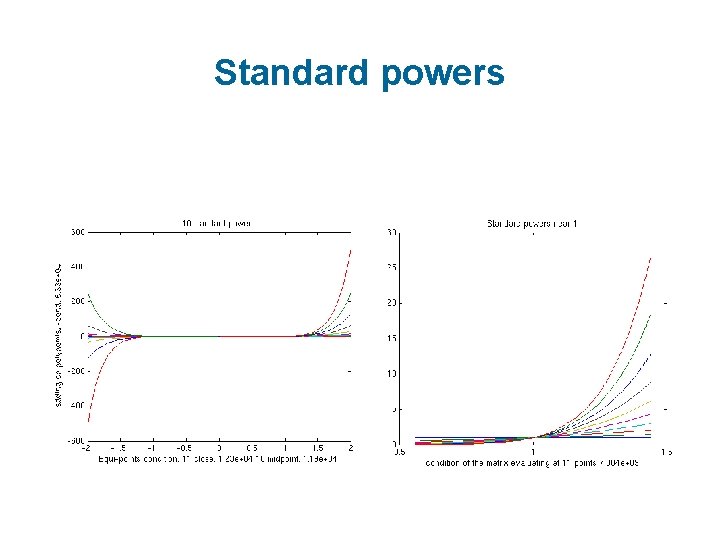
Numerical stability How to avoid numerical problems with high dynamic range of geometric moments?

Standard powers

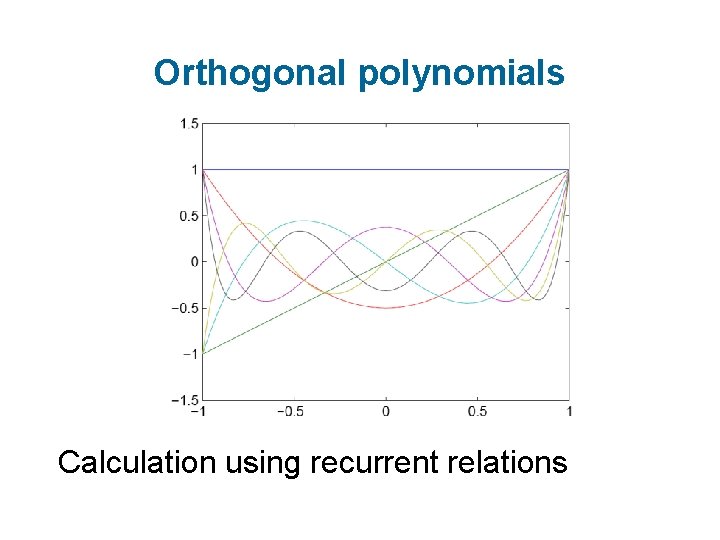
Orthogonal polynomials Calculation using recurrent relations

Two kinds of orthogonality • Moments (polynomials) orthogonal on a unit square • Moments (polynomials) orthogonal on a unit disk

Moments orthogonal on a square is a system of 1 D orthogonal polynomials

Common 1 D orthogonal polynomials • • • Legendre <-1, 1> Chebyshev <-1, 1> Gegenbauer <-1, 1> Jacobi <-1, 1> or <0, 1> (generalized) Laguerre <0, ∞) Hermite (-∞, ∞)

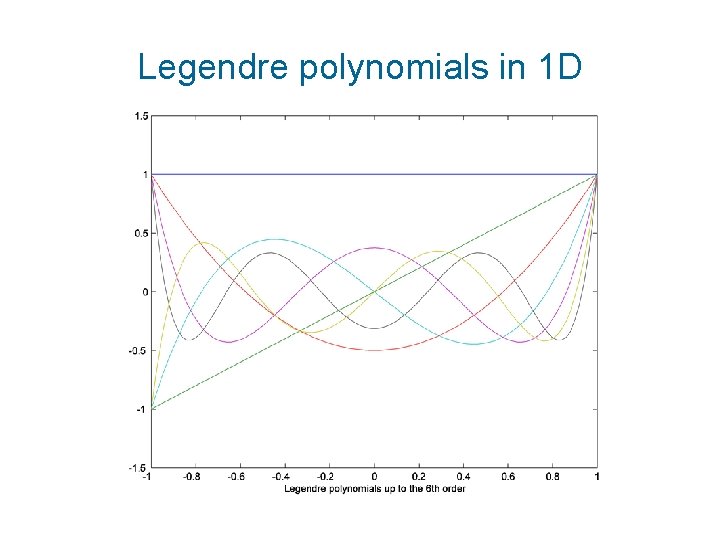
Legendre polynomials Definition Orthogonality
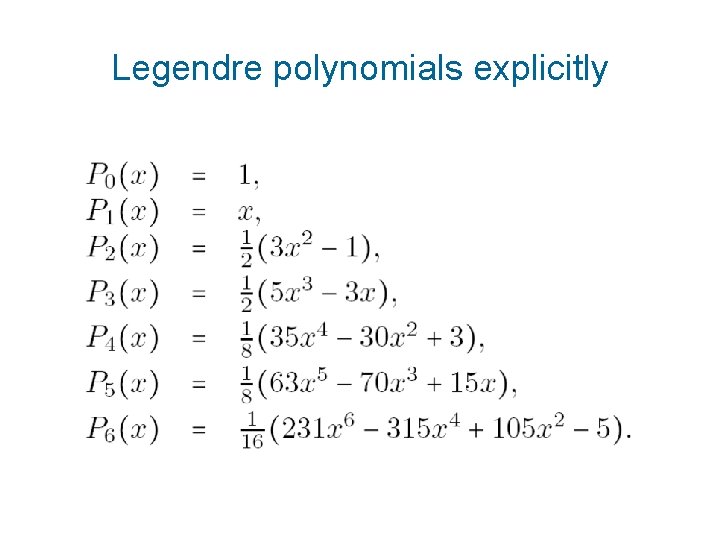
Legendre polynomials explicitly

Legendre polynomials in 1 D

Legendre polynomials in 2 D

Legendre polynomials Explicit formula Recurrence relation

Legendre moments

Legendre and geometric moments

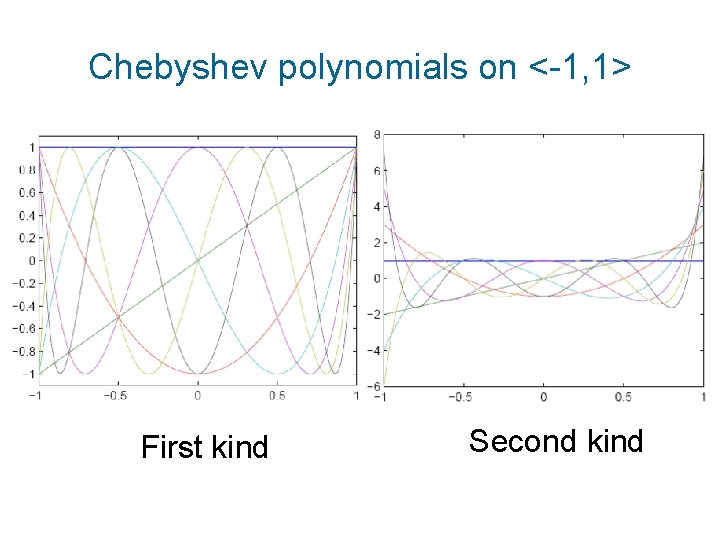
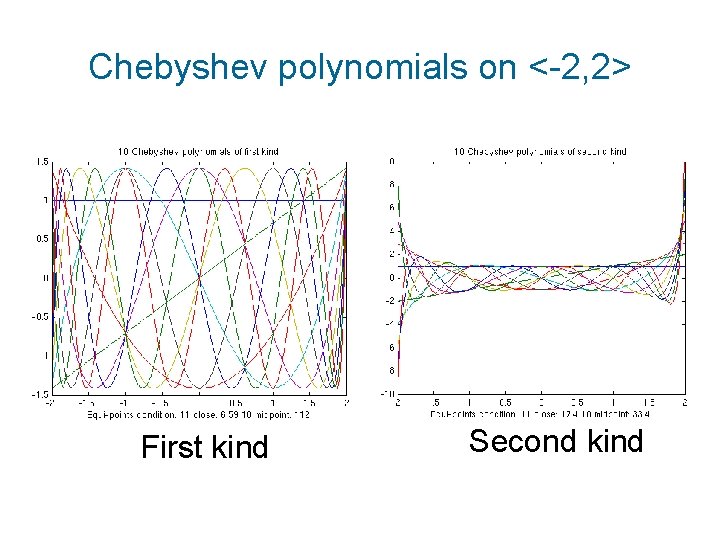
Chebyshev polynomials First kind Second kind

Chebyshev polynomials on <-1, 1> First kind Second kind

Chebyshev polynomials on <-2, 2> First kind Second kind

Chebyshev polynomials in 2 D

Chebyshev polynomials – orthogonality Continuous They can be normalized to discrete orthogonality

Chebyshev moments

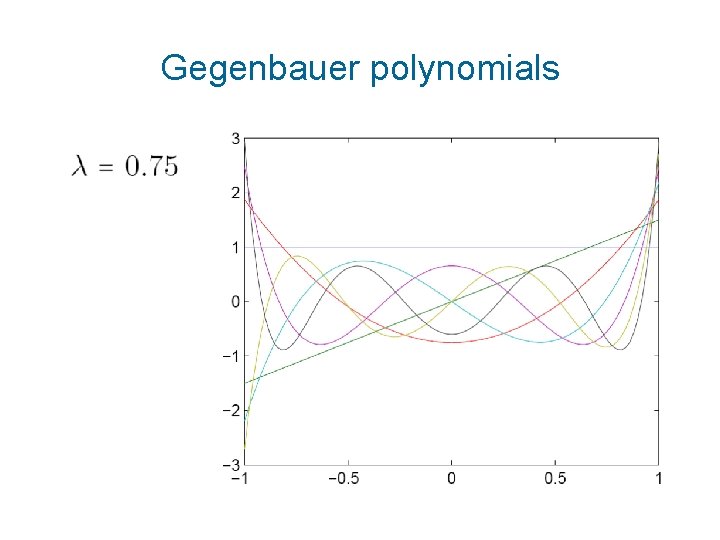
Gegenbauer polynomials Generalization of both Legendre and Chebyshev polynomials – parameter λ - special initial values:

Gegenbauer polynomials

Jacobi polynomials Further generalization, parameters α and β

Laguerre and Hermite polynomials • Infinite interval of orthogonality • Suitable for particular applications only

Discrete OG polynomials on a square Discrete variable Discrete orthogonality

Discrete 1 D OG polynomials • • • Discrete Chebyshev Discrete Laguerre Krawtchouk Hahn Dual-Hahn Racah

Discrete Chebyshev polynomials

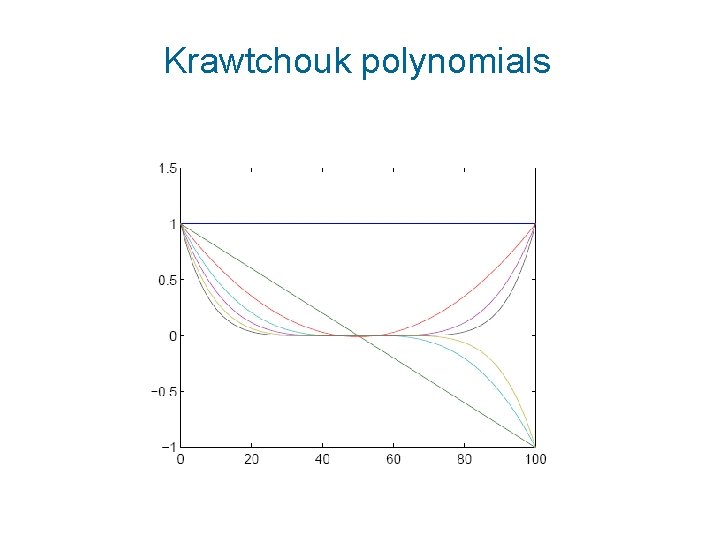
Krawtchouk polynomials

Krawtchouk polynomials

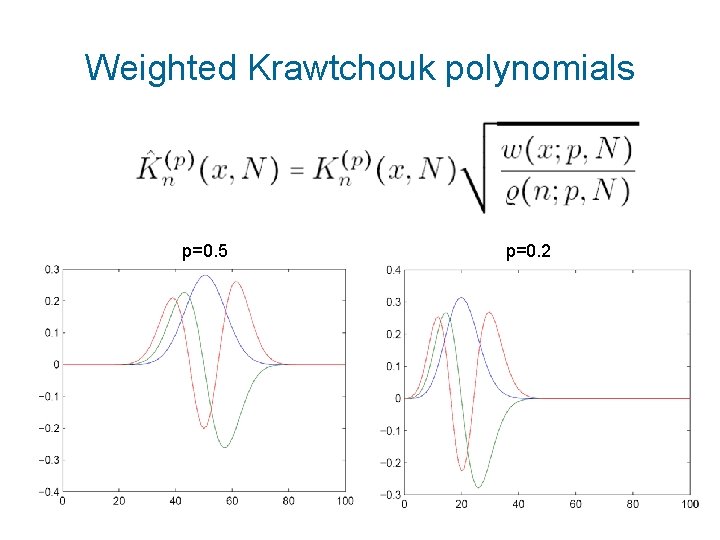
Weighted Krawtchouk polynomials p=0. 5 p=0. 2

Dual-Hahn and Racah polynomials Nonuniform lattice They were adapted such that s is a traditional coordinate in a discrete image.

Moments orthogonal on a disk Radial part Angular part

Moments orthogonal on a disk • • • Zernike Pseudo-Zernike Orthogonal Fourier-Mellin Jacobi-Fourier Chebyshev-Fourier Radial harmonic Fourier

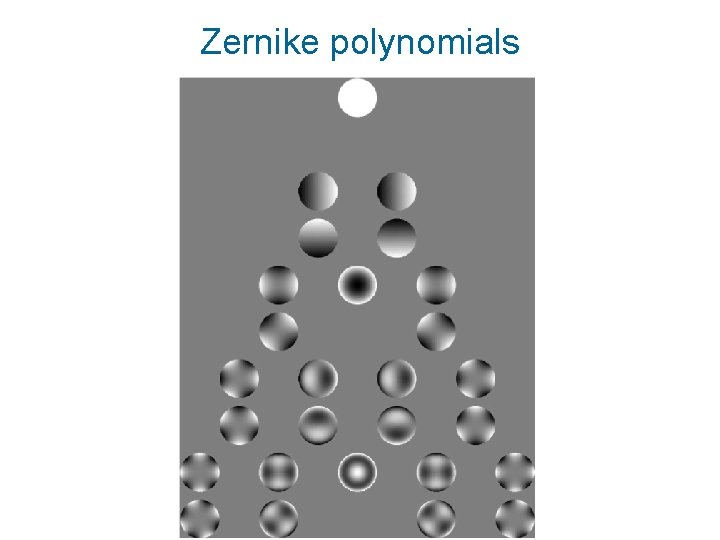
Zernike polynomials Definition Orthogonality

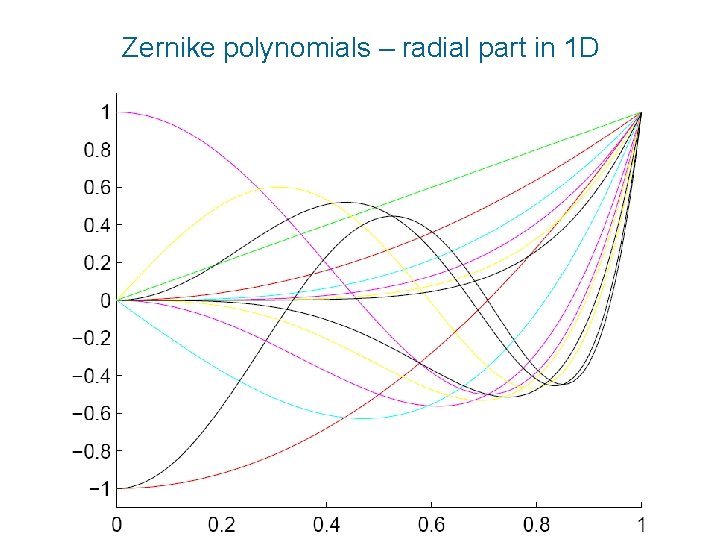
Zernike polynomials – radial part in 1 D

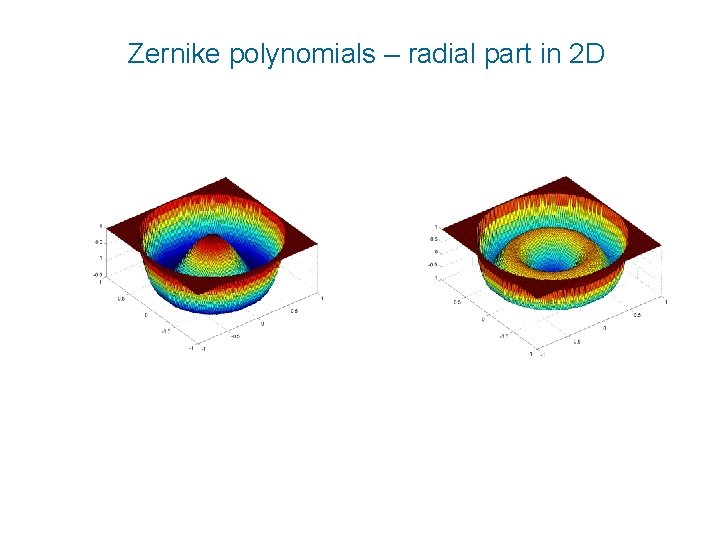
Zernike polynomials – radial part in 2 D

Zernike polynomials

Zernike moments Mapping of Cartesian coordinates x, y to polar coordinates r, φ: • Whole image is mapped inside the unit disk • Translation and scaling invariance

Rotation property of Zernike moments The magnitude is preserved, the phase is shifted by ℓθ. Invariants are constructed by phase cancellation

Zernike rotation invariants Phase cancellation by multiplication Normalization to rotation

Pseudo - Zernike polynomials need not be even → redundancy

Orthogonal Fourier-Mellin moments

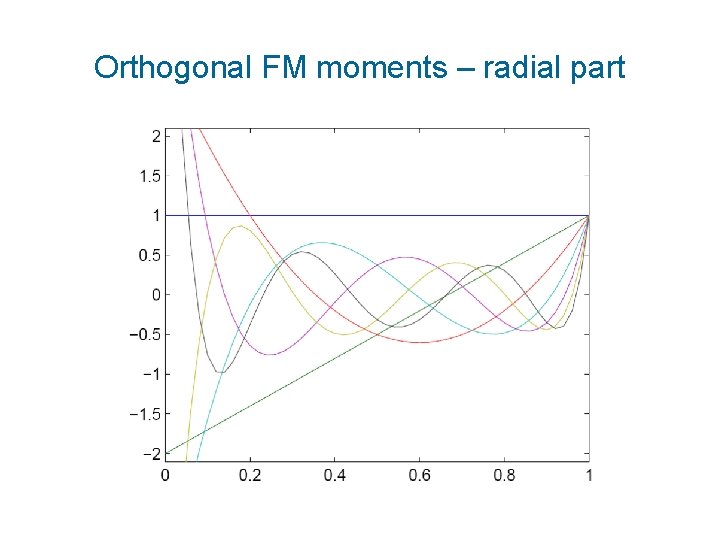
Orthogonal FM moments – radial part

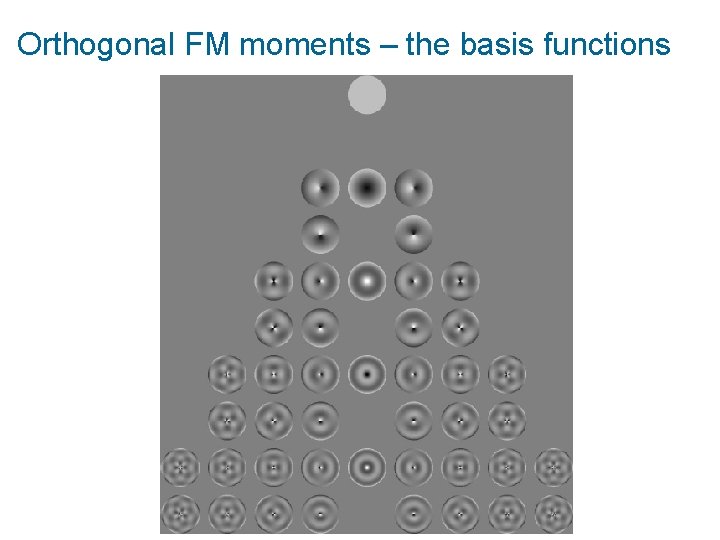
Orthogonal FM moments – the basis functions

Jacobi-Fourier and Chebyshev-Fourier moments Combination: radial part – 1 D orthogonal polynomials angular part – traditional harmonic function 1 D OG polynomials – shifted version: Orthogonality on <0, 1>

Radial harmonic Fourier moments Tn(r) is not polynomial → they are not moments in a strict sense

Recognition by Zernike rotation invariants

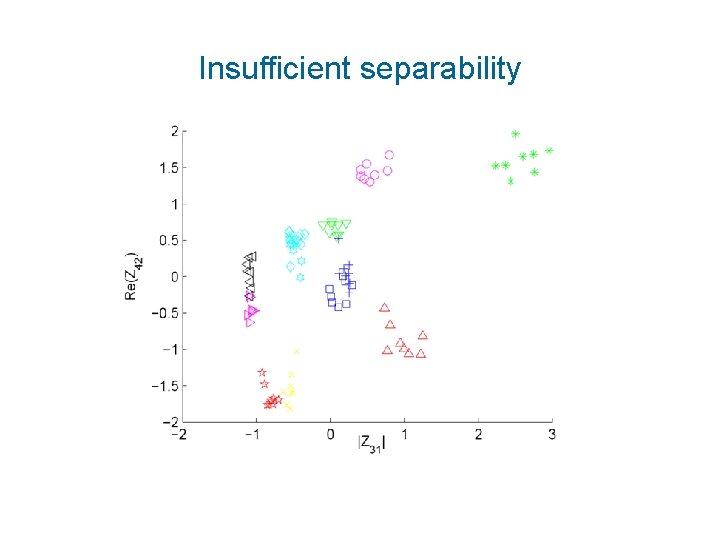
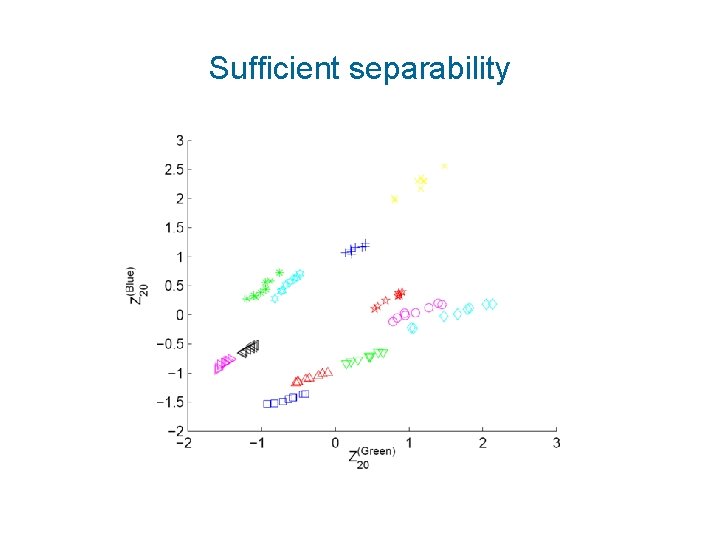
Insufficient separability

Sufficient separability

Image reconstruction • Direct reconstruction from geometric moments • Solution of a system of equations • Works for very small images only • For larger images the system is ill-conditioned

Image reconstruction by direct computation 12 x 12 13 x 13

Image reconstruction • Reconstruction from geometric moments via FT

Image reconstruction via Fourier transform

Image reconstruction • Image reconstruction from OG moments on a square • Image reconstruction from OG moments on a disk (Zernike)

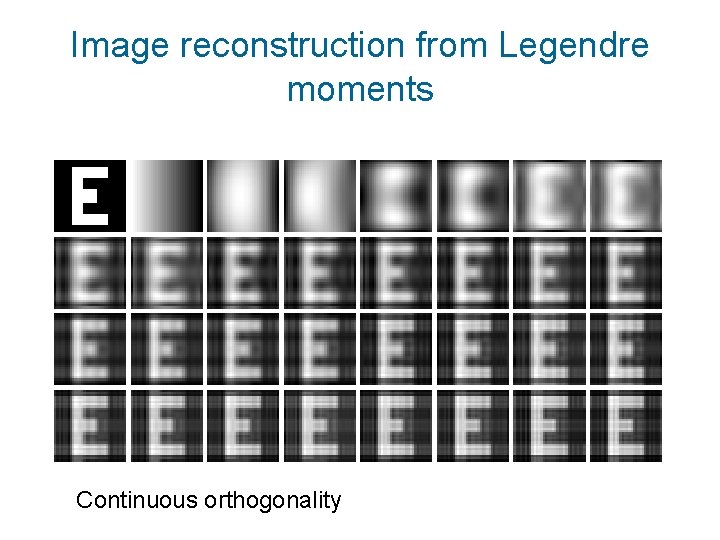
Image reconstruction from Legendre moments Continuous orthogonality

Image reconstruction from Zernike moments Better for polar raster

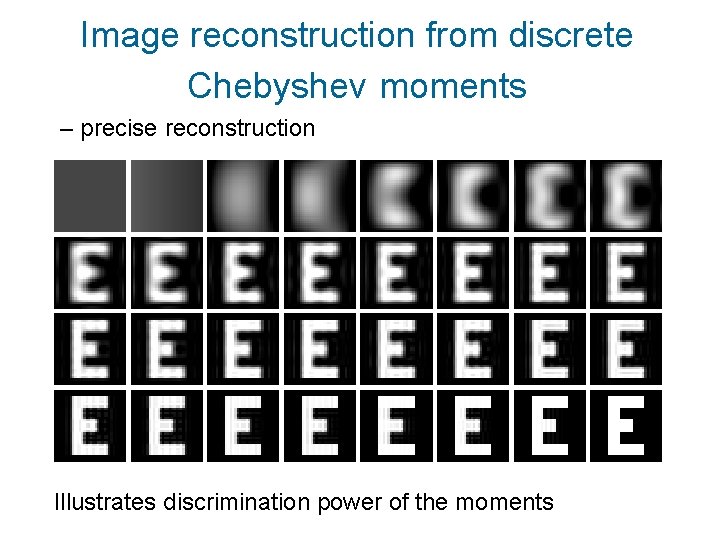
Image reconstruction from discrete Chebyshev moments – precise reconstruction Illustrates discrimination power of the moments

Reconstruction of large images Discrete Chebyshev moments – precise up to 1075 th order Limitation is imposed by floating-point underflow

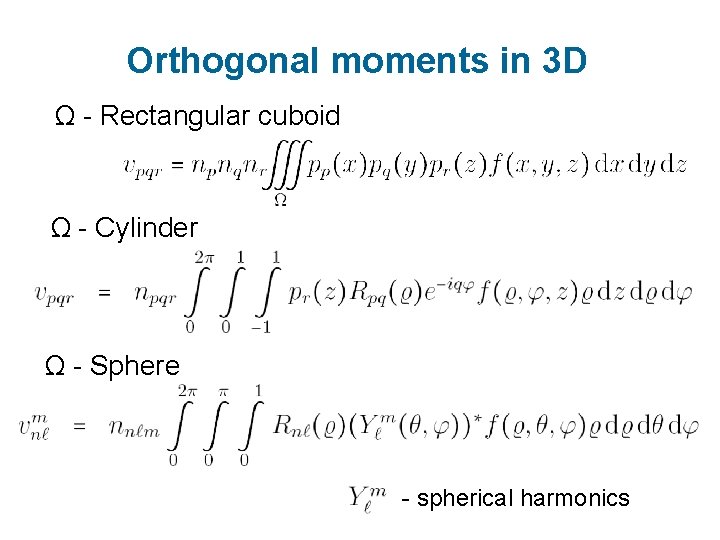
Orthogonal moments in 3 D Ω - Rectangular cuboid Ω - Cylinder Ω - Sphere - spherical harmonics

Example: 3 D Zernike moments

Summary of OG moments • OG moments are used because of their favorable numerical properties, not because of theoretical contribution • OG moments should be never used outside the area of orthogonality • OG moments should be always calculated by recurrent relations, not by expanding into powers • Preferably discrete OG polynomials should be used • Moments OG on a square do not provide easy rotation invariance • Even if the reconstruction from OG moments is seemingly simple, moments are not a good tool for image compression
 The accompanying graph shows marie's distance from home
The accompanying graph shows marie's distance from home John pushes hector on a plastic toboggan
John pushes hector on a plastic toboggan A small child slides down the four frictionless slides
A small child slides down the four frictionless slides Http //mbs.meb.gov.tr/ http //www.alantercihleri.com
Http //mbs.meb.gov.tr/ http //www.alantercihleri.com Siat.ung.ac.id
Siat.ung.ac.id ưu thế lai là gì
ưu thế lai là gì Các môn thể thao bắt đầu bằng tiếng nhảy
Các môn thể thao bắt đầu bằng tiếng nhảy Tư thế ngồi viết
Tư thế ngồi viết Cái miệng nó xinh thế
Cái miệng nó xinh thế Hình ảnh bộ gõ cơ thể búng tay
Hình ảnh bộ gõ cơ thể búng tay Cách giải mật thư tọa độ
Cách giải mật thư tọa độ Tư thế ngồi viết
Tư thế ngồi viết Thẻ vin
Thẻ vin V cc cc
V cc cc Chó sói
Chó sói Thơ thất ngôn tứ tuyệt đường luật
Thơ thất ngôn tứ tuyệt đường luật Hổ sinh sản vào mùa nào
Hổ sinh sản vào mùa nào Từ ngữ thể hiện lòng nhân hậu
Từ ngữ thể hiện lòng nhân hậu Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất Diễn thế sinh thái là
Diễn thế sinh thái là Vẽ hình chiếu vuông góc của vật thể sau
Vẽ hình chiếu vuông góc của vật thể sau Frameset trong html5
Frameset trong html5 101012 bằng
101012 bằng Lời thề hippocrates
Lời thề hippocrates Glasgow thang điểm
Glasgow thang điểm đại từ thay thế
đại từ thay thế Vẽ hình chiếu đứng bằng cạnh của vật thể
Vẽ hình chiếu đứng bằng cạnh của vật thể Quá trình desamine hóa có thể tạo ra
Quá trình desamine hóa có thể tạo ra Công thức tính thế năng
Công thức tính thế năng Thế nào là mạng điện lắp đặt kiểu nổi
Thế nào là mạng điện lắp đặt kiểu nổi Khi nào hổ mẹ dạy hổ con săn mồi
Khi nào hổ mẹ dạy hổ con săn mồi Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Dot
Dot Thế nào là sự mỏi cơ
Thế nào là sự mỏi cơ Bổ thể
Bổ thể Phản ứng thế ankan
Phản ứng thế ankan Thiếu nhi thế giới liên hoan
Thiếu nhi thế giới liên hoan Chúa yêu trần thế
Chúa yêu trần thế điện thế nghỉ
điện thế nghỉ Một số thể thơ truyền thống
Một số thể thơ truyền thống Trời xanh đây là của chúng ta thể thơ
Trời xanh đây là của chúng ta thể thơ Hệ hô hấp
Hệ hô hấp Số nguyên tố là số gì
Số nguyên tố là số gì đặc điểm cơ thể của người tối cổ
đặc điểm cơ thể của người tối cổ Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Phối cảnh
Phối cảnh Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Cas clinique neurologie
Cas clinique neurologie Cas clinique insuffisance cardiaque
Cas clinique insuffisance cardiaque Cas concret asg
Cas concret asg Preseljevanje slovanov
Preseljevanje slovanov Internal control revenue cycle
Internal control revenue cycle Nursing cas gpa calculator
Nursing cas gpa calculator Caslabs
Caslabs Future continuous
Future continuous Cas orbitopatia tiroidea
Cas orbitopatia tiroidea Si vous auriez besoin
Si vous auriez besoin étude de cas lagos 4ème
étude de cas lagos 4ème Gradjansko vaspitanje za 1. razred osnovne skole
Gradjansko vaspitanje za 1. razred osnovne skole Diagramme de cas d'utilisation acteur secondaire
Diagramme de cas d'utilisation acteur secondaire Signature
Signature Calrai
Calrai Pásmový čas příklady
Pásmový čas příklady Dans le cas
Dans le cas Wiris desktop
Wiris desktop Sci fider
Sci fider

























































































