Graphs Chapter 7 Visit for more Learning Resources

Graphs Chapter 7 Visit for more Learning Resources

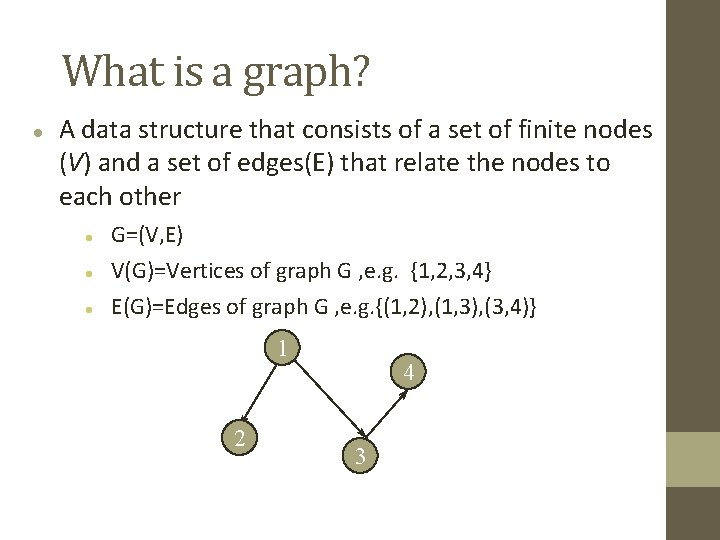
What is a graph? A data structure that consists of a set of finite nodes (V) and a set of edges(E) that relate the nodes to each other G=(V, E) V(G)=Vertices of graph G , e. g. {1, 2, 3, 4} E(G)=Edges of graph G , e. g. {(1, 2), (1, 3), (3, 4)} 1 2 4 3

Graphs • Vertices are also called nodes and points. • E is the edge set. • Each edge connects two different vertices. • Edges are also called arcs and lines. • Directed edge has an orientation (u, v). u v

Graphs • Undirected edge has no orientation (u, v). u v • Undirected graph => no oriented edge. • Directed graph => every edge has an orientation.

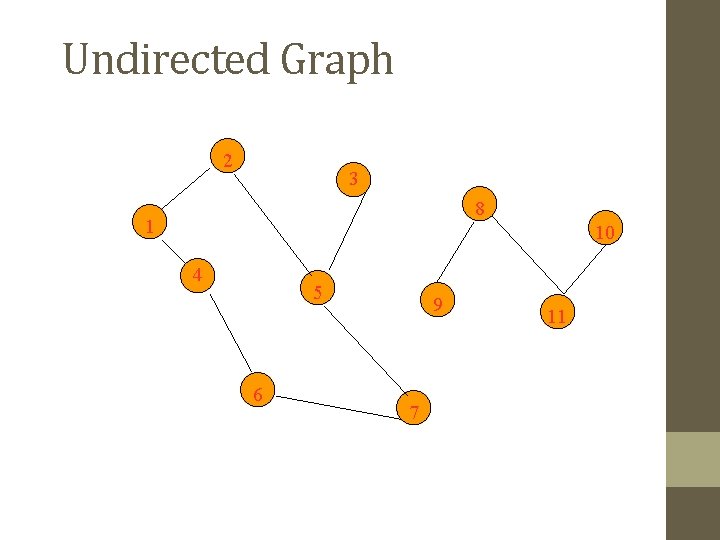
Undirected Graph 2 3 8 1 10 4 5 6 9 7 11

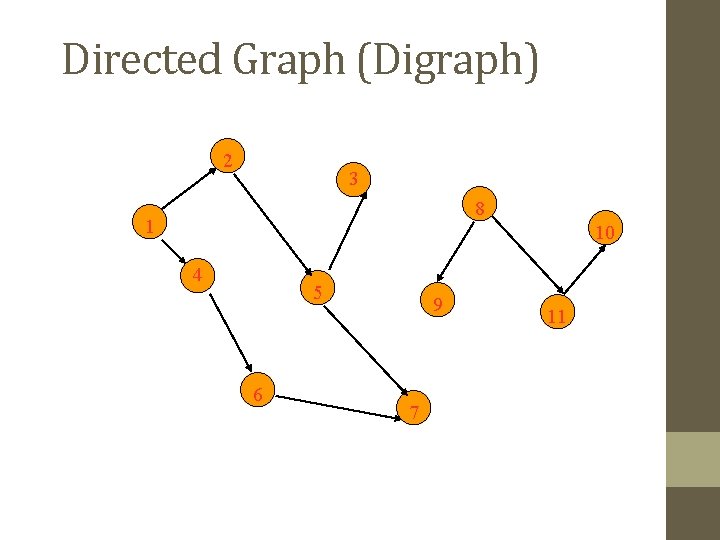
Directed Graph (Digraph) 2 3 8 1 10 4 5 6 9 7 11

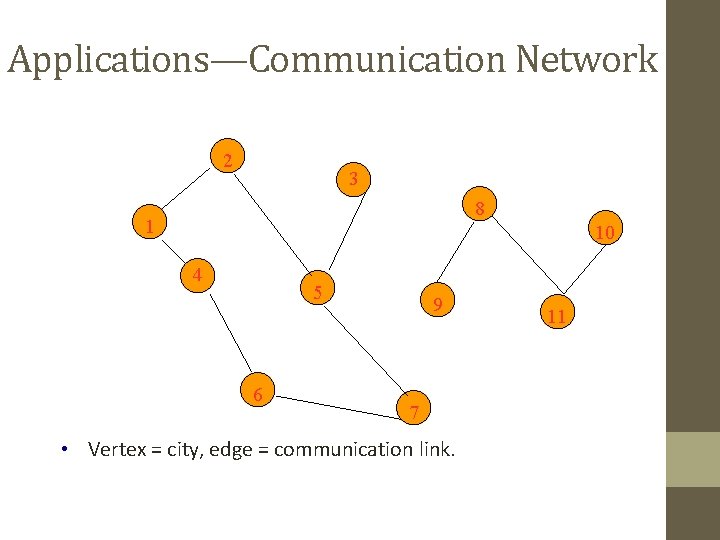
Applications—Communication Network 2 3 8 1 10 4 5 6 9 7 • Vertex = city, edge = communication link. 11

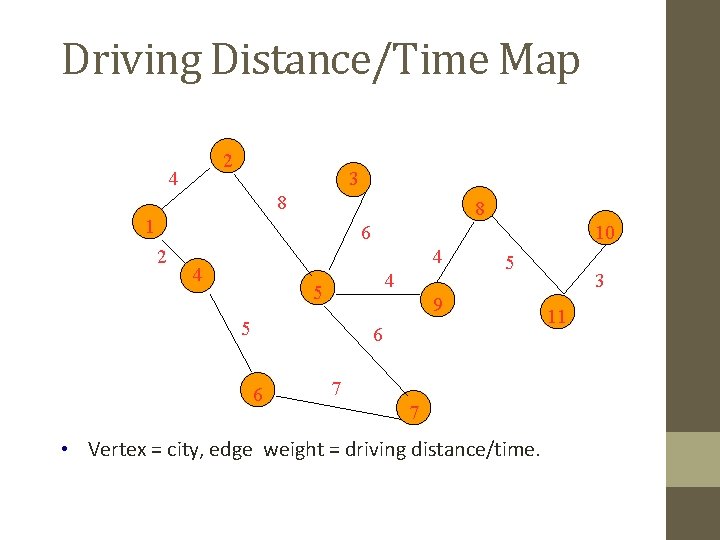
Driving Distance/Time Map 2 4 3 8 8 1 6 2 10 4 4 4 5 5 9 5 6 6 7 7 • Vertex = city, edge weight = driving distance/time. 3 11

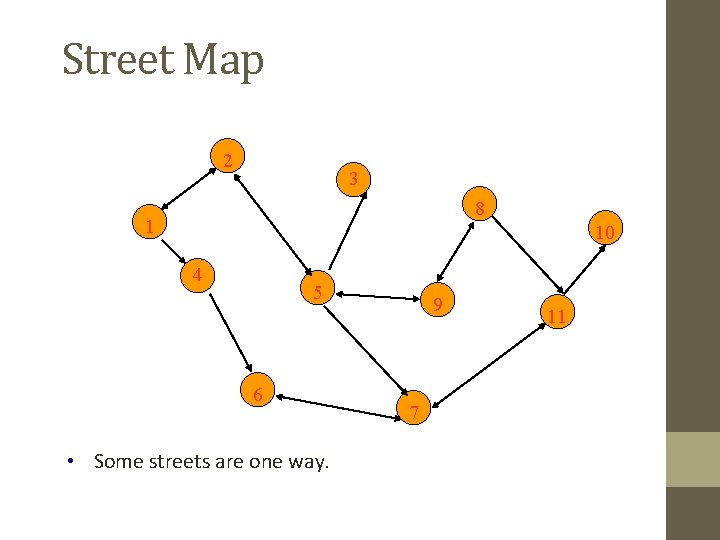
Street Map 2 3 8 1 10 4 5 6 • Some streets are one way. 9 7 11

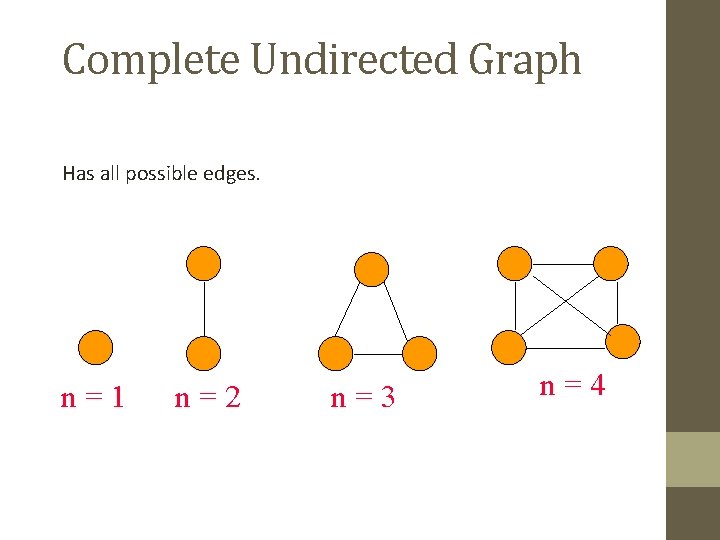
Complete Undirected Graph Has all possible edges. n=1 n=2 n=3 n=4

Number Of Edges—Undirected Graph • Each edge is of the form (u, v) • Number of such pairs in an n vertex graph is n(n-1). • Since edge (u, v) is the same as edge (v, u), the number of edges in a complete undirected graph is n(n-1)/2. • Number of edges in an undirected graph is <= n(n-1)/2.

Number Of Edges—Directed Graph • Each edge is of the form (u, v), u != v. • Number of such pairs in an n vertex graph is n(n-1). • Since edge (u, v) is not the same as edge (v, u), the number of edges in a complete directed graph is n(n-1). • Number of edges in a directed graph is <= n(n-1).

Graph terminology 1. Adjacent nodes: two nodes are adjacent if they are connected by an edge 2. Path: A sequence of edges that connect two nodes in a graph 3. Path Length: Total no of edges included in path. 4. Complete graph: a graph in which every vertex is directly connected to every other vertex 5 is adjacent to 7 7 is adjacent from 5

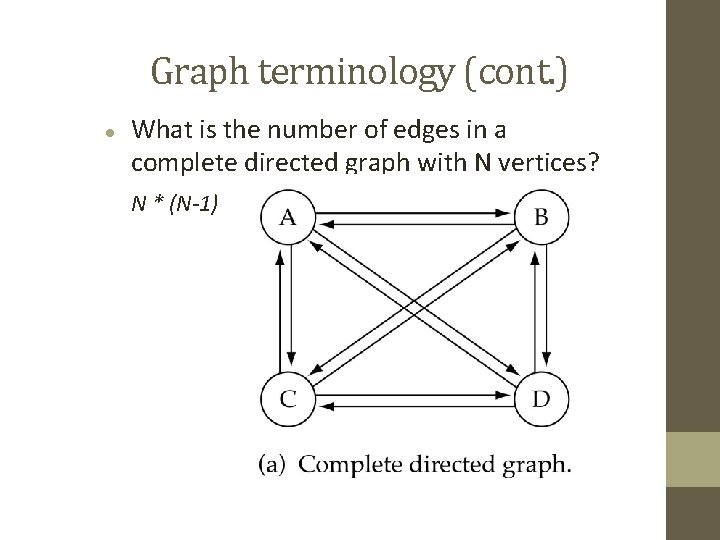
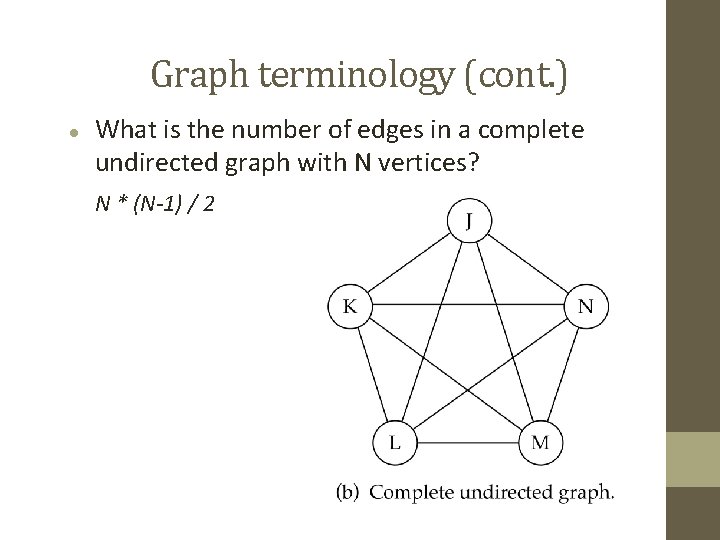
Graph terminology (cont. ) What is the number of edges in a complete directed graph with N vertices? N * (N-1)

Graph terminology (cont. ) What is the number of edges in a complete undirected graph with N vertices? N * (N-1) / 2

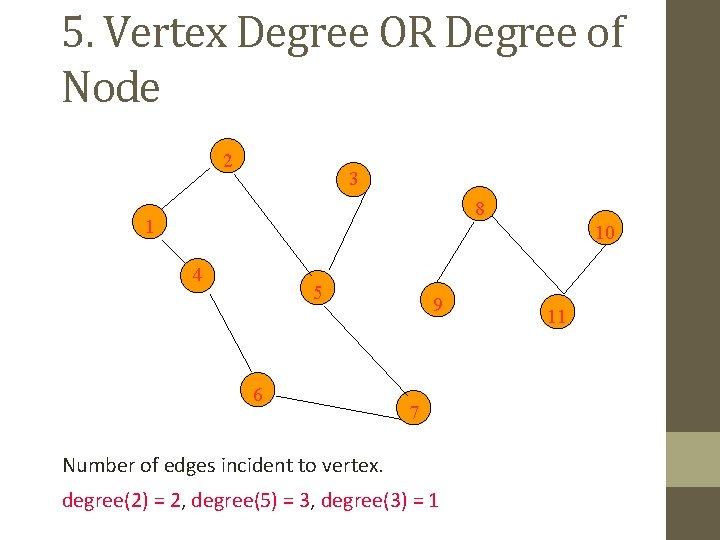
5. Vertex Degree OR Degree of Node 2 3 8 1 10 4 5 6 9 7 Number of edges incident to vertex. degree(2) = 2, degree(5) = 3, degree(3) = 1 11

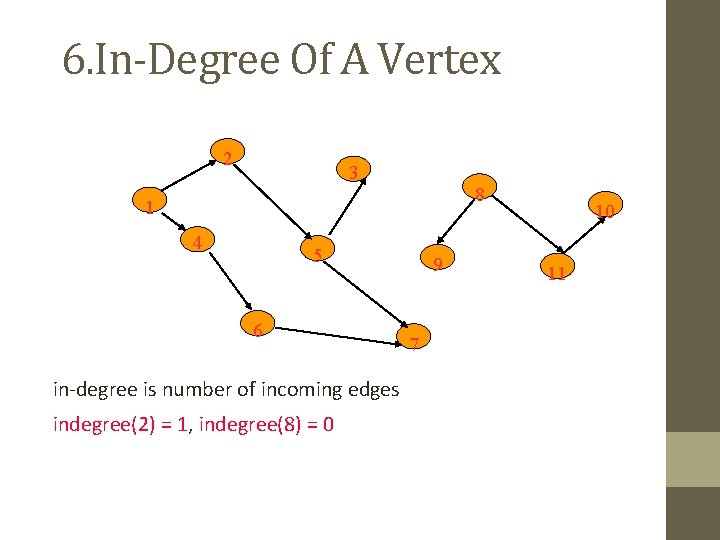
6. In-Degree Of A Vertex 2 3 8 1 4 5 6 in-degree is number of incoming edges indegree(2) = 1, indegree(8) = 0 9 7 10 11

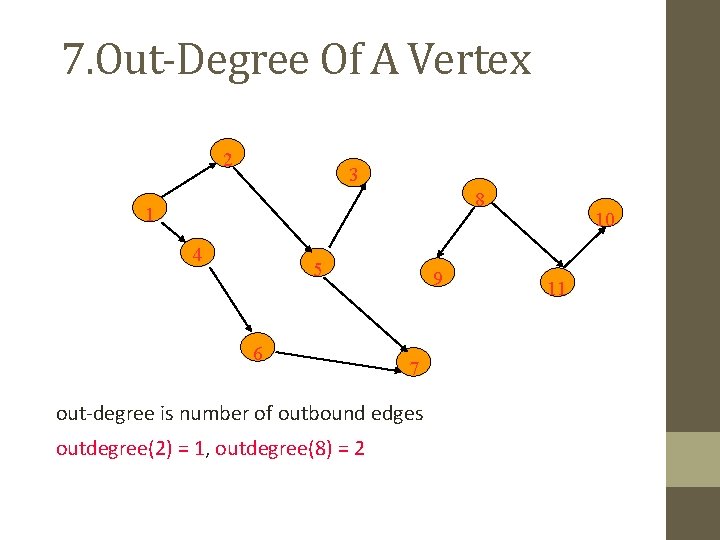
7. Out-Degree Of A Vertex 2 3 8 1 4 5 6 9 7 out-degree is number of outbound edges outdegree(2) = 1, outdegree(8) = 2 10 11

Graph terminology (cont. ) 8. Source: A Node which has only outgoing edges. 9. Sink: A Node which has only Incoming edges. 10. Pendant Node: if indegree of node is 1 and outdegree is 0 then it is pendant Node. 11. Reachable: If path exist between two nodes then they are reachable.

Graph terminology (cont. ) 12. Sling or loop: An edge of graph which joins a node to itself is called sling or loop. 13. Parallel Edges: The two distinct edges between a pair to nodes which are opposite in a direction. 14. Weighted Edge: edge has Numerical Values. 15. Isolated Node: Not an Adjacent node of any other node

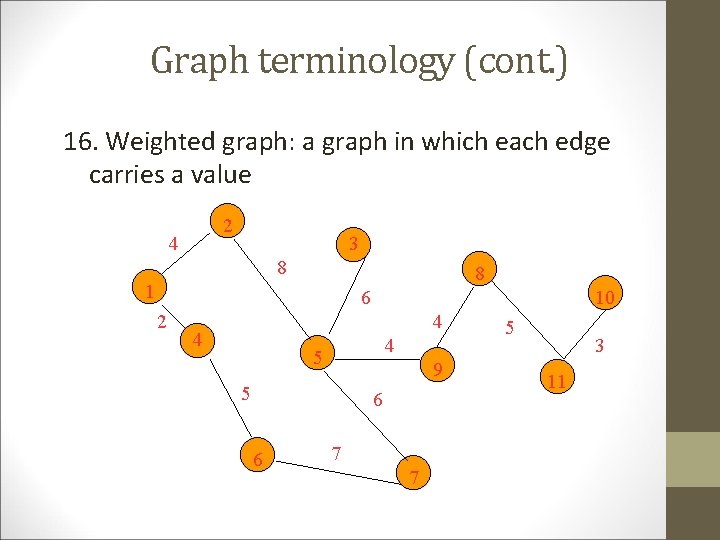
Graph terminology (cont. ) 16. Weighted graph: a graph in which each edge carries a value 2 4 3 8 8 1 6 2 10 4 4 4 5 9 5 6 6 7 7 5 3 11

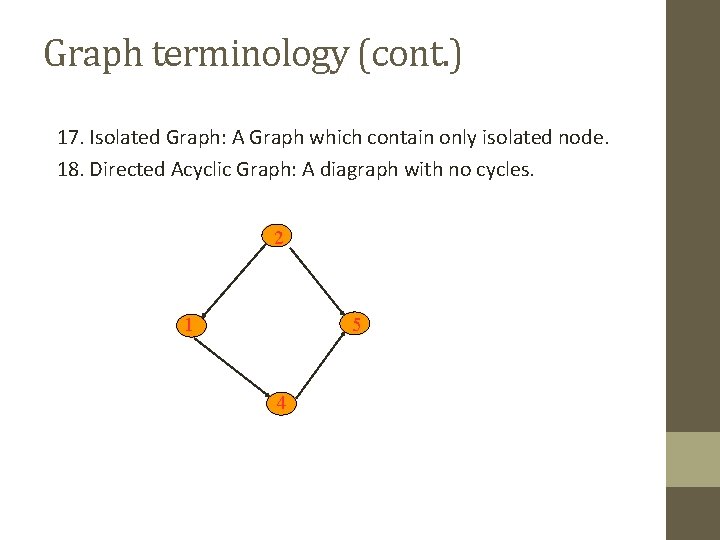
Graph terminology (cont. ) 17. Isolated Graph: A Graph which contain only isolated node. 18. Directed Acyclic Graph: A diagraph with no cycles. 2 1 5 4

Graph implementation Array-based implementation A 1 D array is used to represent the vertices A 2 D array (adjacency matrix) is used to represent the edges

Graph Representation There are two ways to represent the Graph: 1. 2. Sequential Representation 1. Adjacency Matrix 2. Path Matrix Adjacency Lists/Linked List representation.

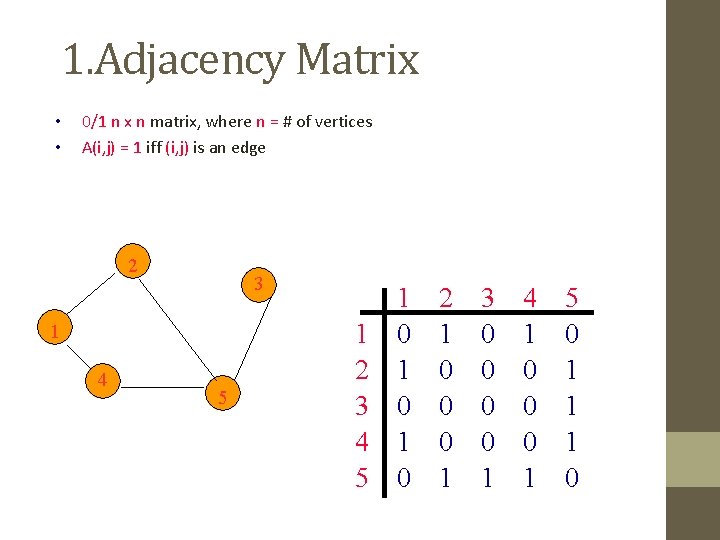
1. Adjacency Matrix • • 0/1 n x n matrix, where n = # of vertices A(i, j) = 1 iff (i, j) is an edge 2 3 1 4 5 1 2 3 4 5 1 0 1 0 2 1 0 0 0 1 3 0 0 1 4 1 0 0 0 1 5 0 1 1 1 0

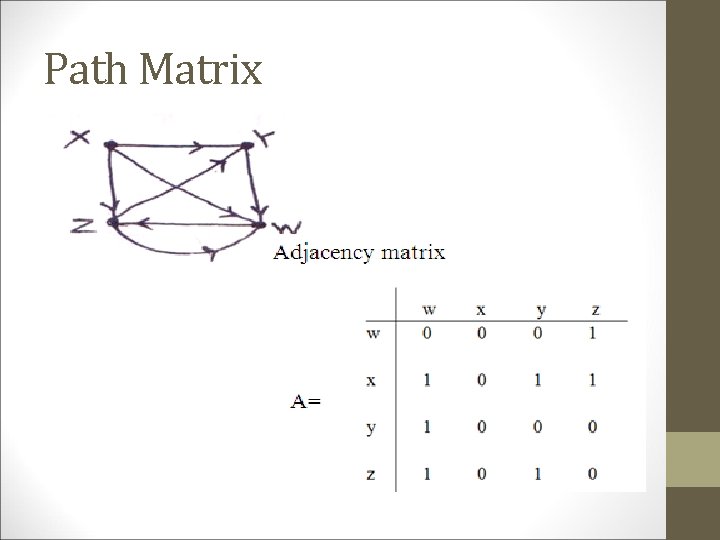
Path Matrix

Path Matrix

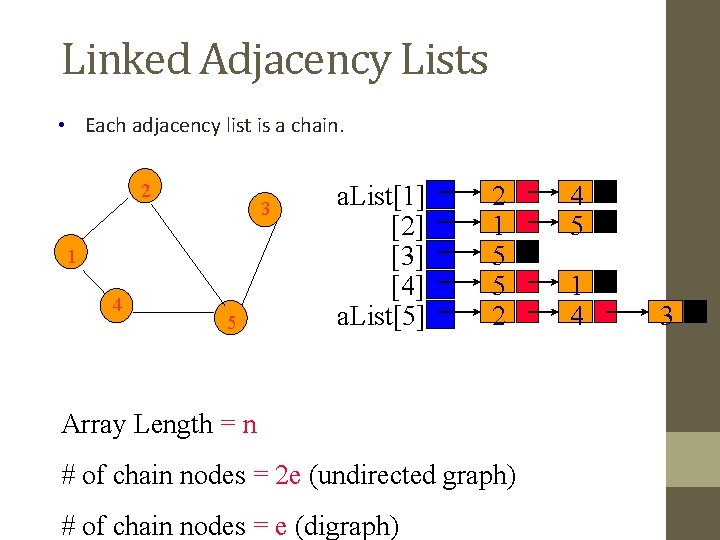
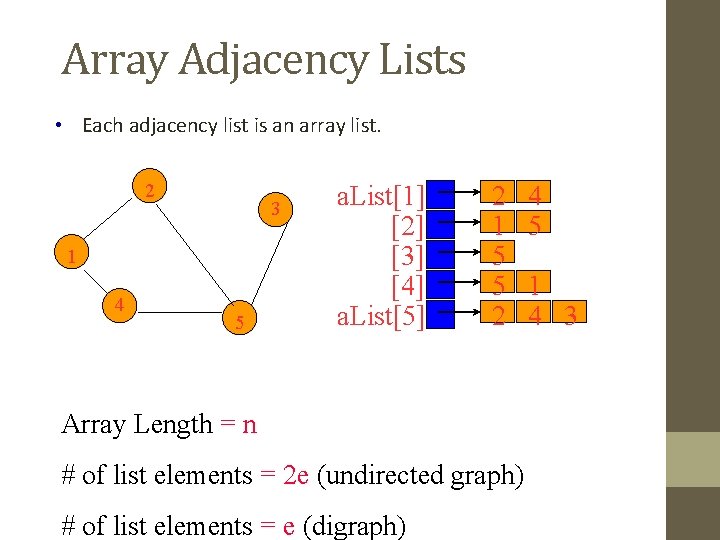
Adjacency Lists • Adjacency list for vertex i is a linear list of vertices adjacent from vertex i. • An array of n adjacency lists. a. List[1] = (2, 4) 2 3 a. List[2] = (1, 5) a. List[3] = (5) 1 4 a. List[4] = (5, 1) 5 a. List[5] = (2, 4, 3)

Adjacency Lists Representation • A graph of n nodes is represented by a one-dimensional array L of linked lists, where • L[i] is the linked list containing all the nodes adjacent from node i. • The nodes in the list L[i] are in no particular order

Example of List L[0]: empty L[1]: empty L[2]: 0, 1, 4, 5 L[3]: 0, 1, 4, 5 L[4]: 0, 1 L[5]: 0, 1 Mary 0 Helen 1 Joe 3 John 2 Tom 4 Paul 5

Linked Adjacency Lists • Each adjacency list is a chain. 2 3 1 4 5 a. List[1] [2] [3] [4] a. List[5] 2 1 5 5 2 Array Length = n # of chain nodes = 2 e (undirected graph) # of chain nodes = e (digraph) 4 5 1 4 3

Array Adjacency Lists • Each adjacency list is an array list. 2 3 1 4 5 a. List[1] [2] [3] [4] a. List[5] 2 1 5 5 2 Array Length = n # of list elements = 2 e (undirected graph) # of list elements = e (digraph) 4 5 1 4 3

Graph Search (traversal) • How do we search a graph? • At a particular vertices, where shall we go next? • Two common Methods: § Breadth-first search (BFS) § Depth-first search (DFS) • In BFS, one explore a graph level by level away (explore all neighbors first and then move on) • In DFS, go as far as possible along a single path until reach a dead end (a vertex with no edge out or no neighbor unexplored) then backtrack Data Structure and Algorithm

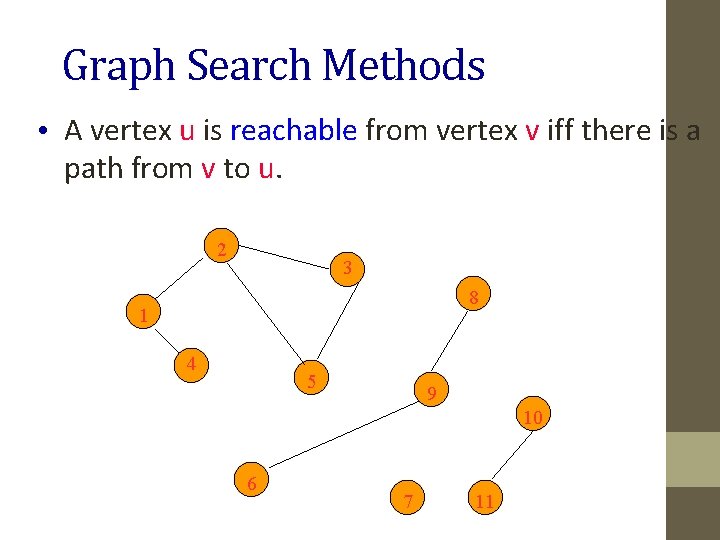
Graph Search Methods • A vertex u is reachable from vertex v iff there is a path from v to u. 2 3 8 1 4 5 9 10 6 7 11

Graph Search Methods • A search method starts at a given vertex v and visits/labels/marks every vertex that is reachable from v. 2 3 8 1 4 5 9 10 6 7 11

Breadth-First Search • Visit start vertex and put into a FIFO queue. • Repeatedly remove a vertex from the queue, visit its unvisited adjacent vertices, put newly visited vertices into the queue.

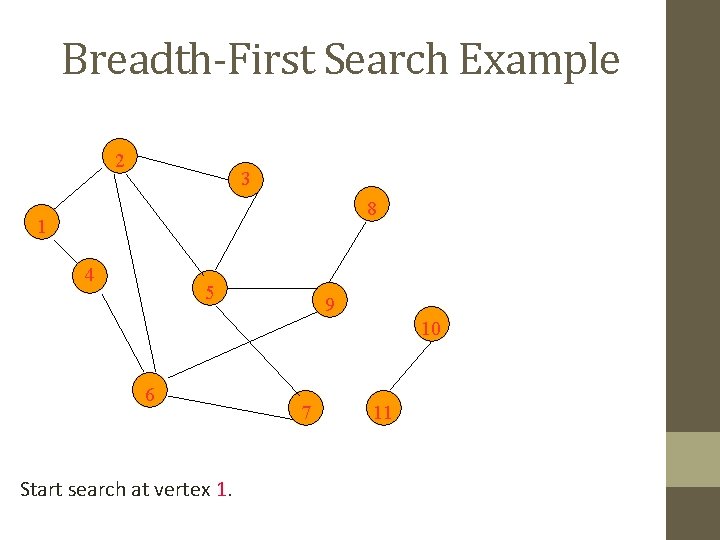
Breadth-First Search Example 2 3 8 1 4 5 9 10 6 Start search at vertex 1. 7 11

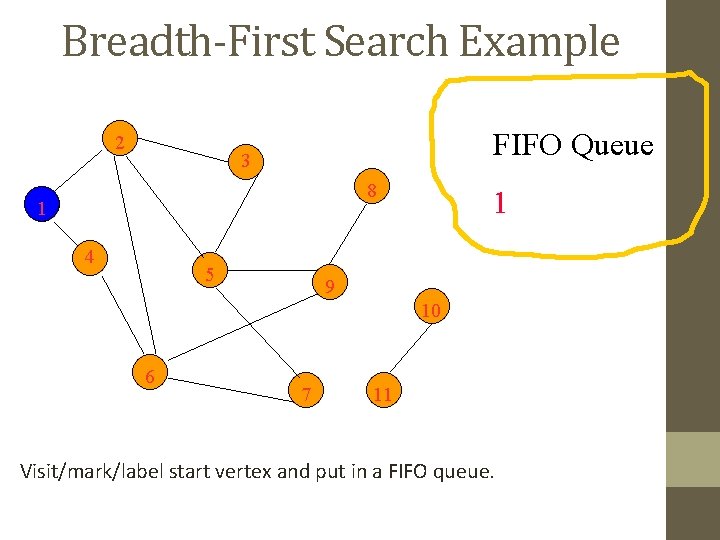
Breadth-First Search Example 2 FIFO Queue 3 8 1 4 5 1 9 10 6 7 11 Visit/mark/label start vertex and put in a FIFO queue.

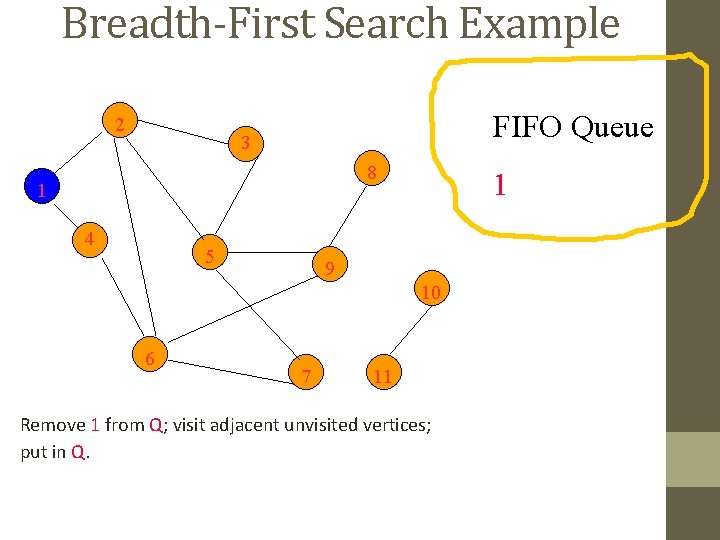
Breadth-First Search Example 2 FIFO Queue 3 8 1 4 5 1 9 10 6 7 11 Remove 1 from Q; visit adjacent unvisited vertices; put in Q.

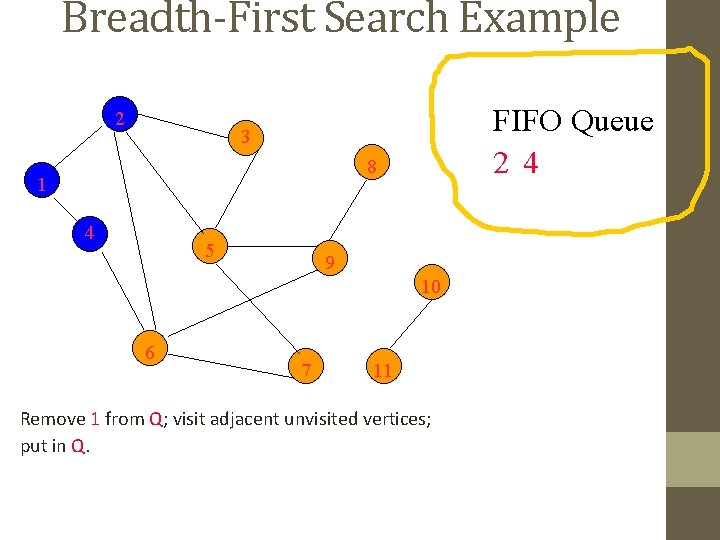
Breadth-First Search Example 2 FIFO Queue 2 4 3 8 1 4 5 9 10 6 7 11 Remove 1 from Q; visit adjacent unvisited vertices; put in Q.

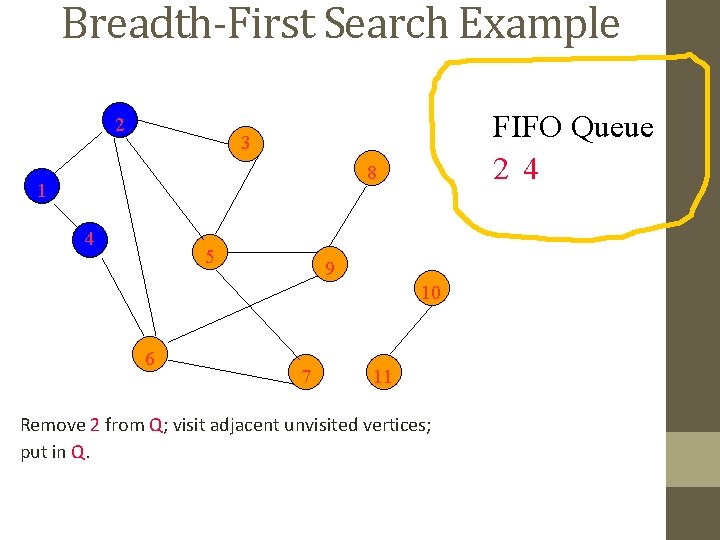
Breadth-First Search Example 2 FIFO Queue 2 4 3 8 1 4 5 9 10 6 7 11 Remove 2 from Q; visit adjacent unvisited vertices; put in Q.

Breadth-First Search Example 2 FIFO Queue 4 5 3 6 3 8 1 4 5 9 10 6 7 11 Remove 2 from Q; visit adjacent unvisited vertices; put in Q.

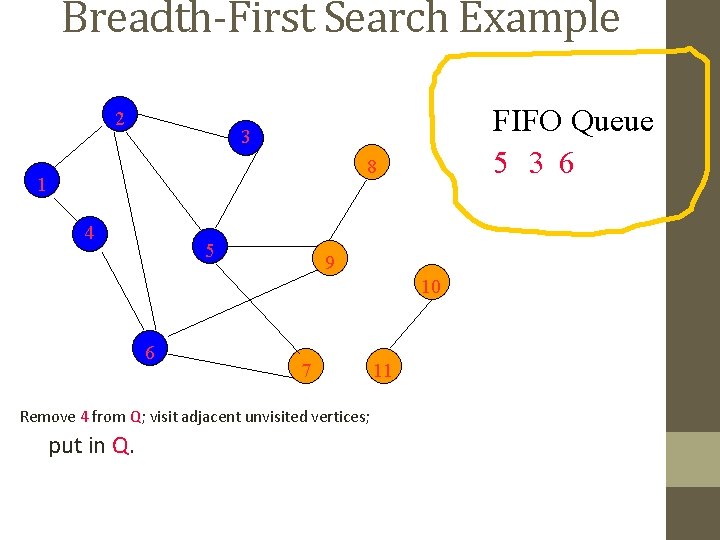
Breadth-First Search Example 2 FIFO Queue 4 5 3 6 3 8 1 4 5 9 10 6 7 11 Remove 4 from Q; visit adjacent unvisited vertices; put in Q.

Breadth-First Search Example 2 FIFO Queue 5 3 6 3 8 1 4 5 9 10 6 7 Remove 4 from Q; visit adjacent unvisited vertices; put in Q. 11

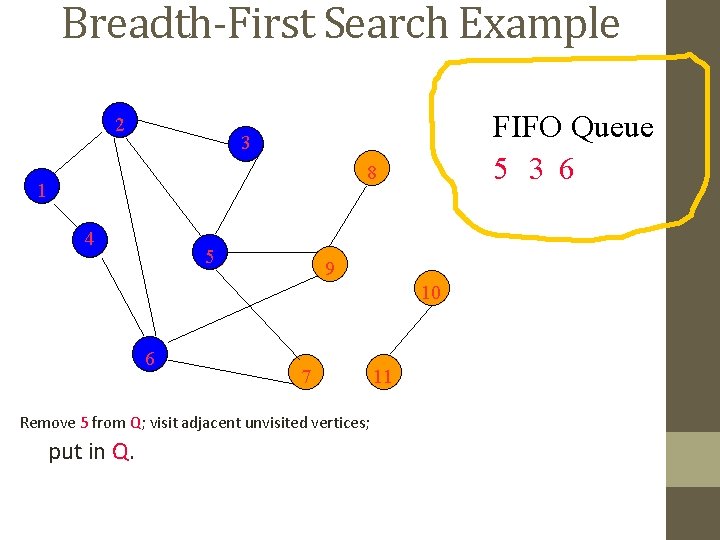
Breadth-First Search Example 2 FIFO Queue 5 3 6 3 8 1 4 5 9 10 6 7 Remove 5 from Q; visit adjacent unvisited vertices; put in Q. 11

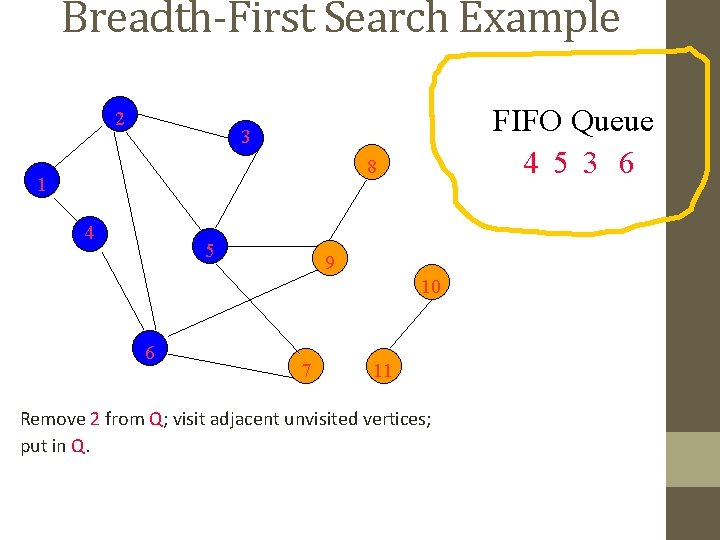
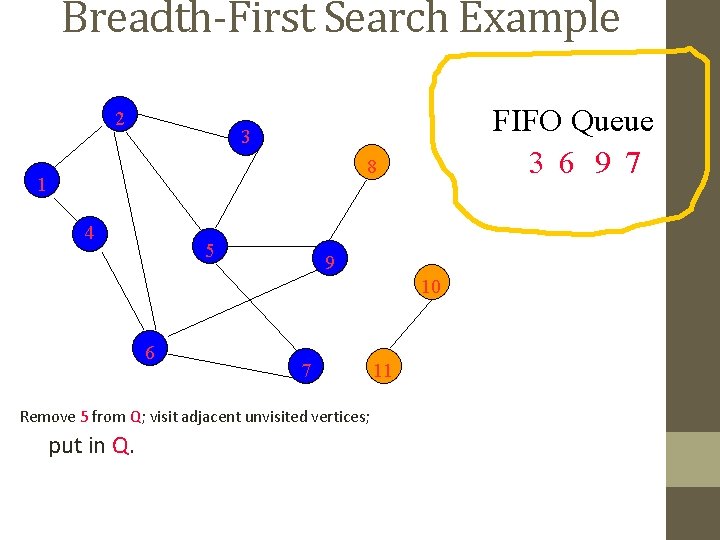
Breadth-First Search Example 2 FIFO Queue 3 6 9 7 3 8 1 4 5 9 10 6 7 Remove 5 from Q; visit adjacent unvisited vertices; put in Q. 11

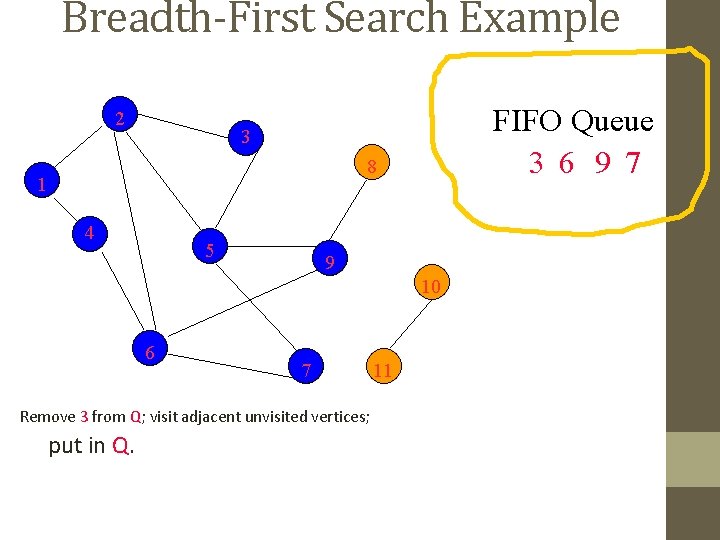
Breadth-First Search Example 2 FIFO Queue 3 6 9 7 3 8 1 4 5 9 10 6 7 Remove 3 from Q; visit adjacent unvisited vertices; put in Q. 11

Breadth-First Search Example 2 FIFO Queue 6 9 7 3 8 1 4 5 9 10 6 7 Remove 3 from Q; visit adjacent unvisited vertices; put in Q. 11

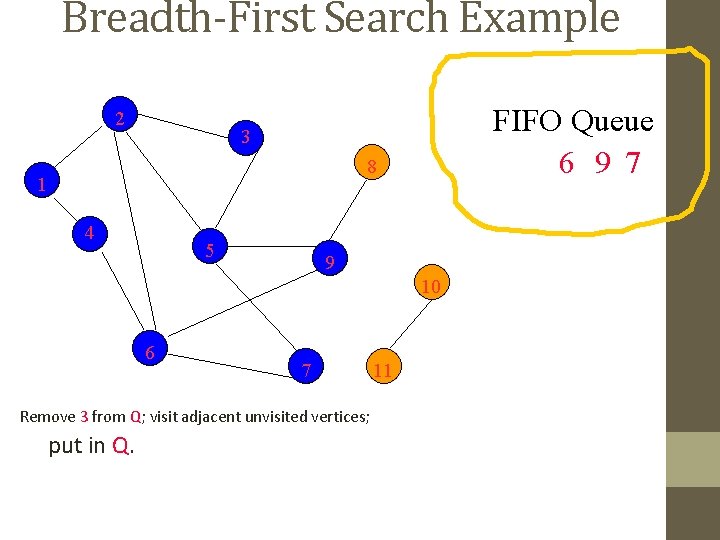
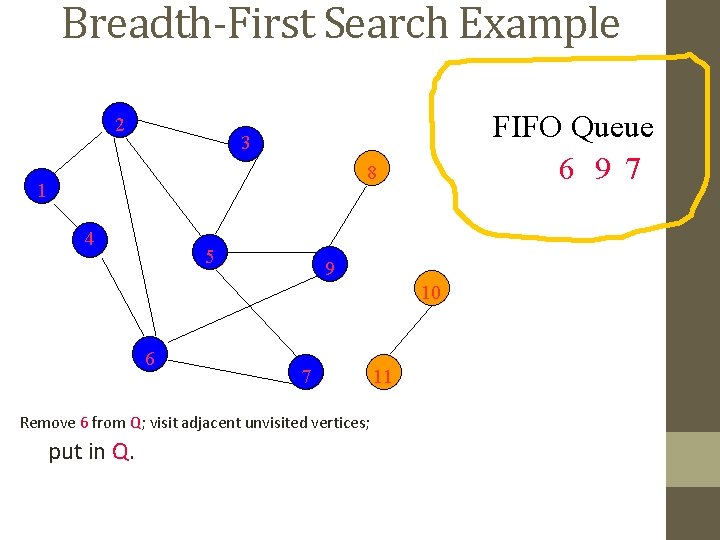
Breadth-First Search Example 2 FIFO Queue 6 9 7 3 8 1 4 5 9 10 6 7 Remove 6 from Q; visit adjacent unvisited vertices; put in Q. 11

Breadth-First Search Example 2 FIFO Queue 9 7 3 8 1 4 5 9 10 6 7 Remove 6 from Q; visit adjacent unvisited vertices; put in Q. 11

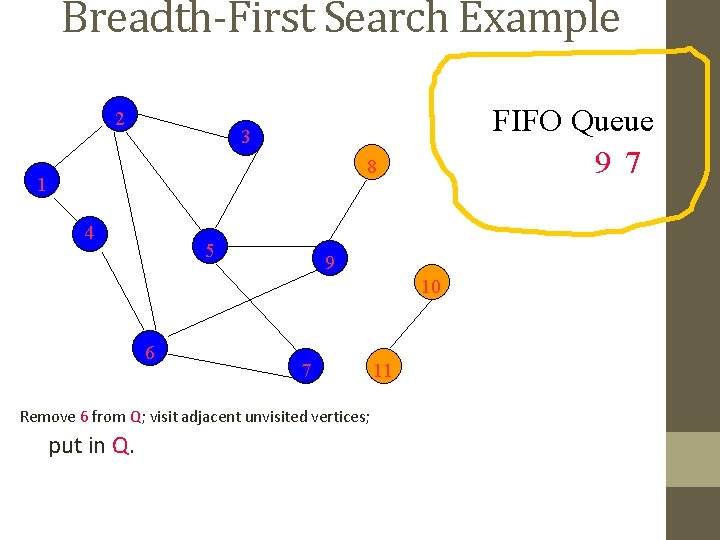
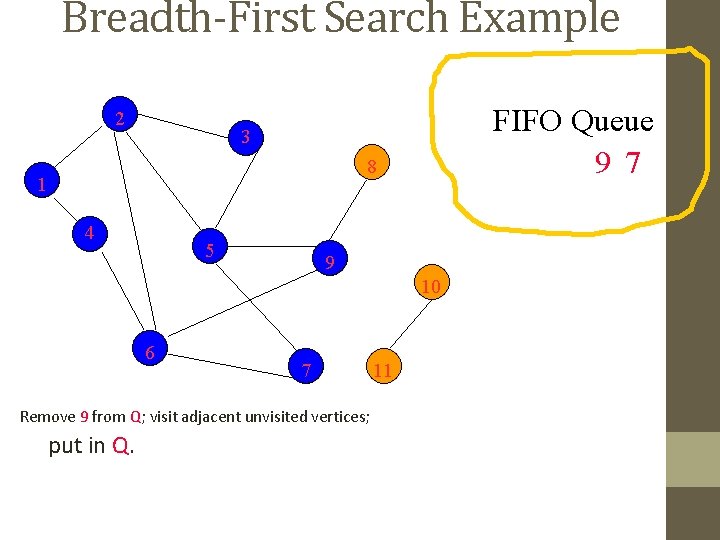
Breadth-First Search Example 2 FIFO Queue 9 7 3 8 1 4 5 9 10 6 7 Remove 9 from Q; visit adjacent unvisited vertices; put in Q. 11

Breadth-First Search Example 2 FIFO Queue 7 8 3 8 1 4 5 9 10 6 7 Remove 9 from Q; visit adjacent unvisited vertices; put in Q. 11

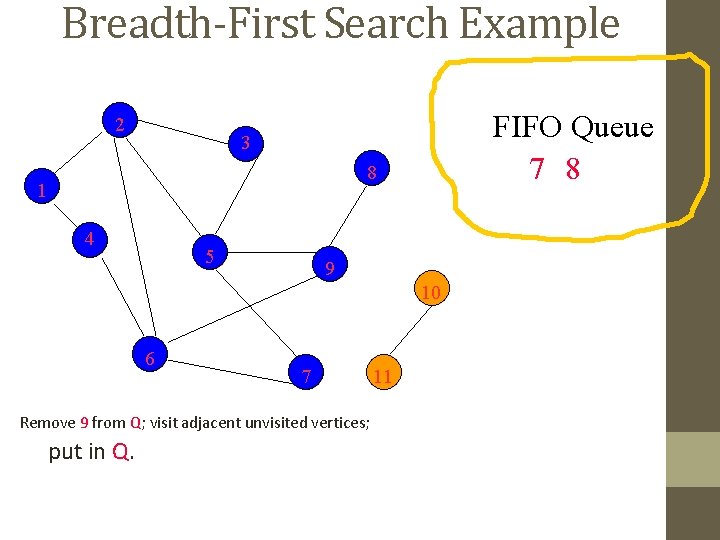
Breadth-First Search Example 2 FIFO Queue 7 8 3 8 1 4 5 9 10 6 7 Remove 7 from Q; visit adjacent unvisited vertices; put in Q. 11

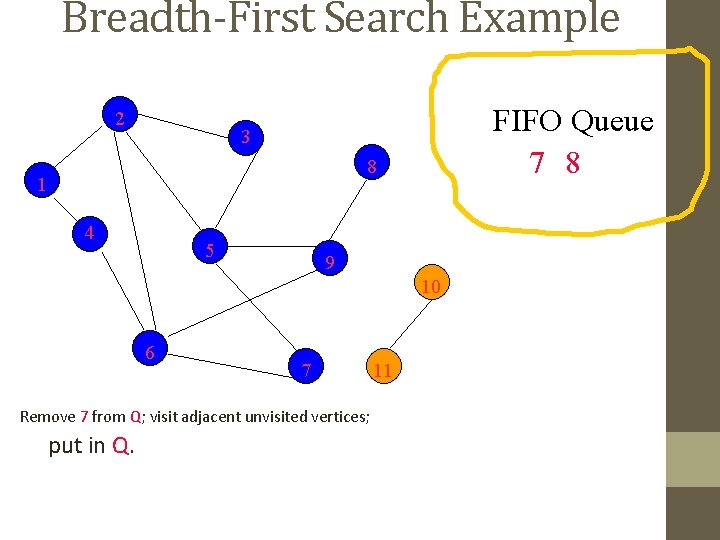
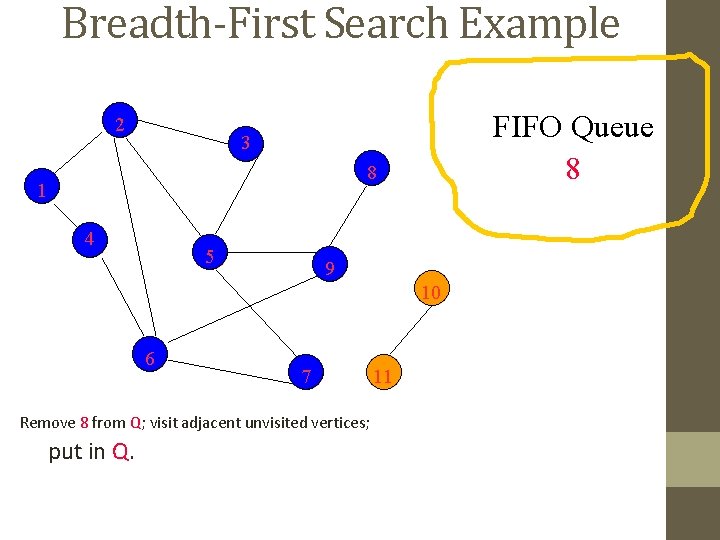
Breadth-First Search Example 2 FIFO Queue 8 3 8 1 4 5 9 10 6 7 Remove 7 from Q; visit adjacent unvisited vertices; put in Q. 11

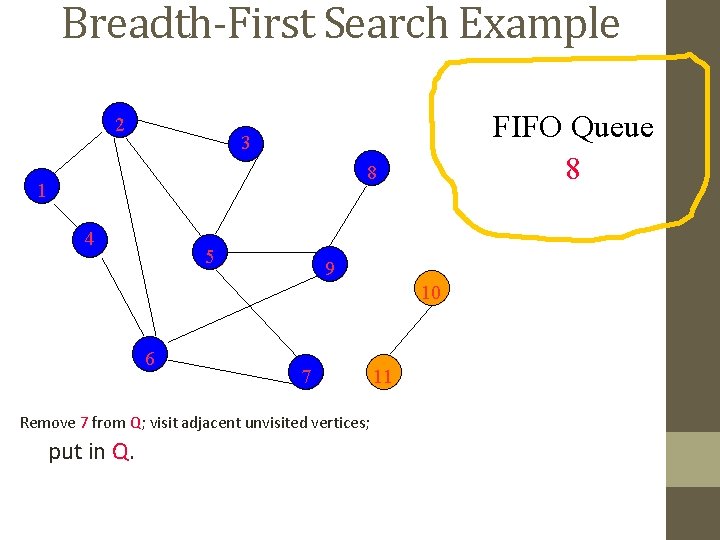
Breadth-First Search Example 2 FIFO Queue 8 3 8 1 4 5 9 10 6 7 Remove 8 from Q; visit adjacent unvisited vertices; put in Q. 11

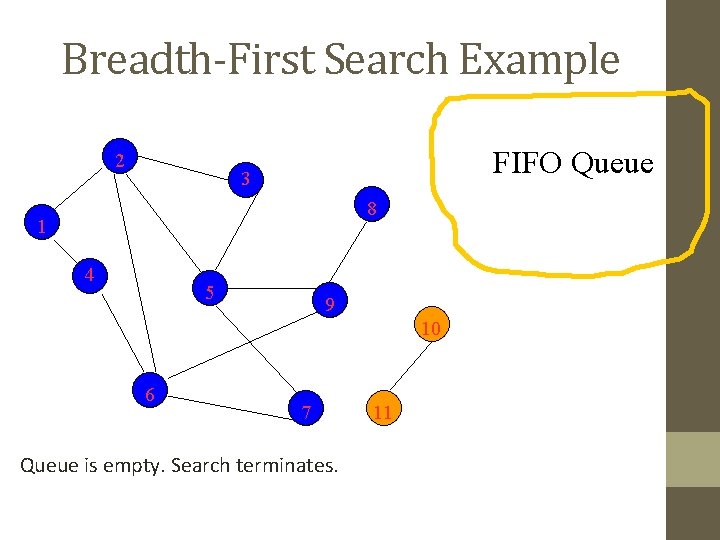
Breadth-First Search Example 2 FIFO Queue 3 8 1 4 5 9 10 6 7 Queue is empty. Search terminates. 11

Breadth-First Search Property • All vertices reachable from the start vertex (including the start vertex) are visited.

Breadth-first Search (BFS) • Search for all vertices that are directly reachable from the root (called level 1 vertices) • After mark all these vertices, visit all vertices that are directly reachable from any level 1 vertices (called level 2 vertices), and so on. Data Structure and Algorithm

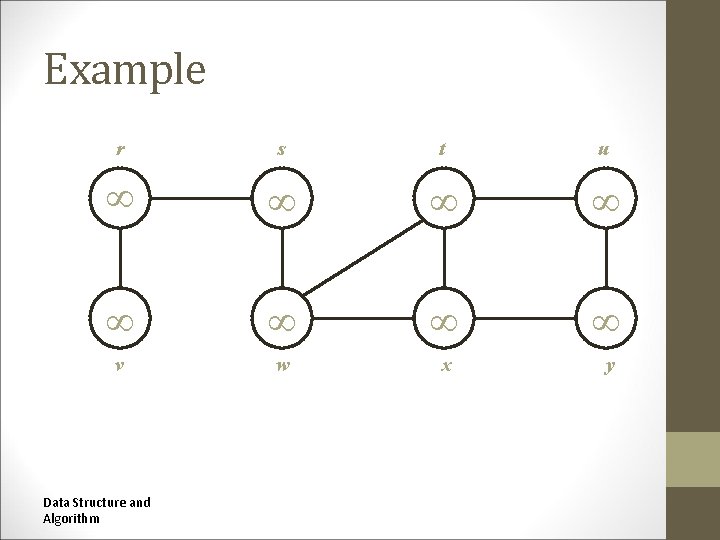
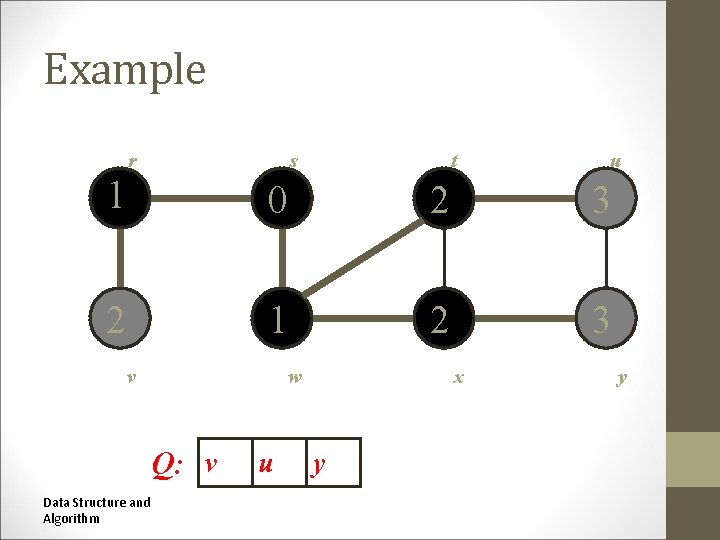
Example r s t u v w x y Data Structure and Algorithm

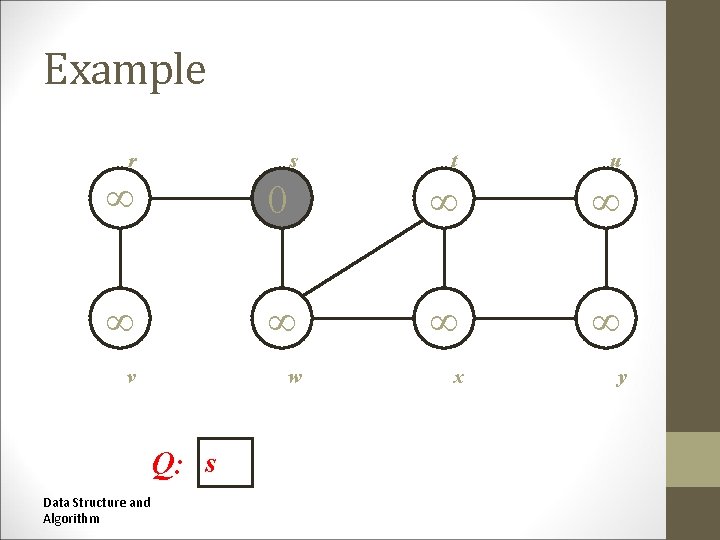
Example r s t t u u 0 x y v w w v Q: s Data Structure and Algorithm x y

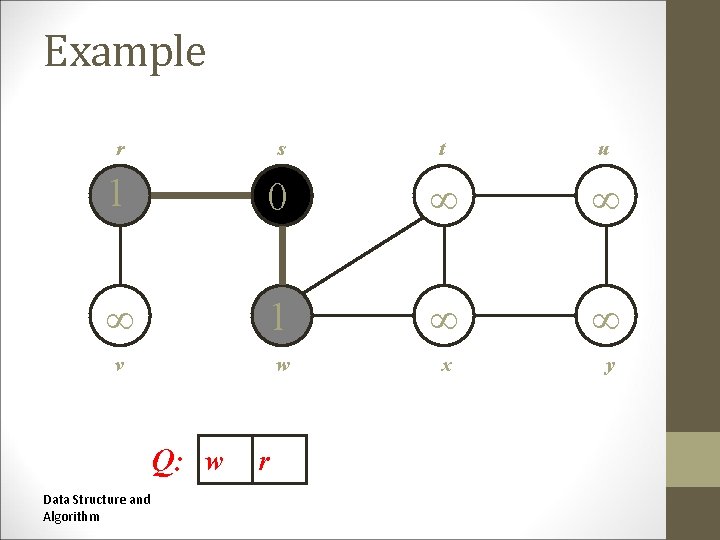
Example r s t u 1 0 1 v w x y Q: w Data Structure and Algorithm r

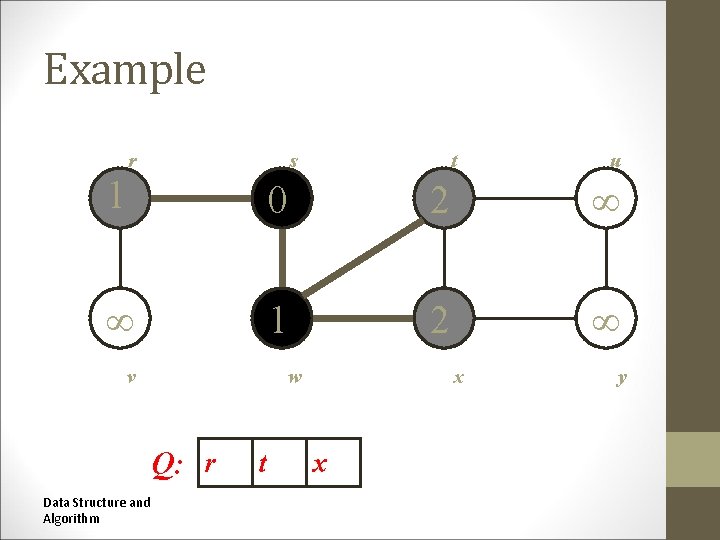
Example r s r t s t u u 1 0 2 1 2 v w w v Q: r Data Structure and Algorithm t x x x y y

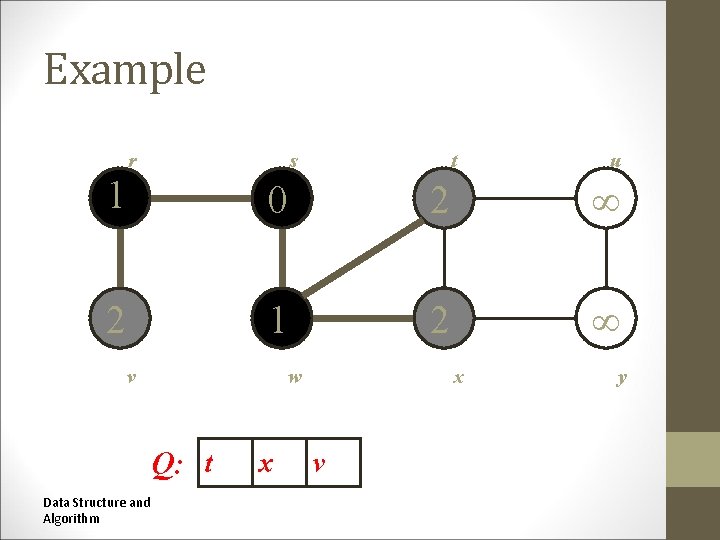
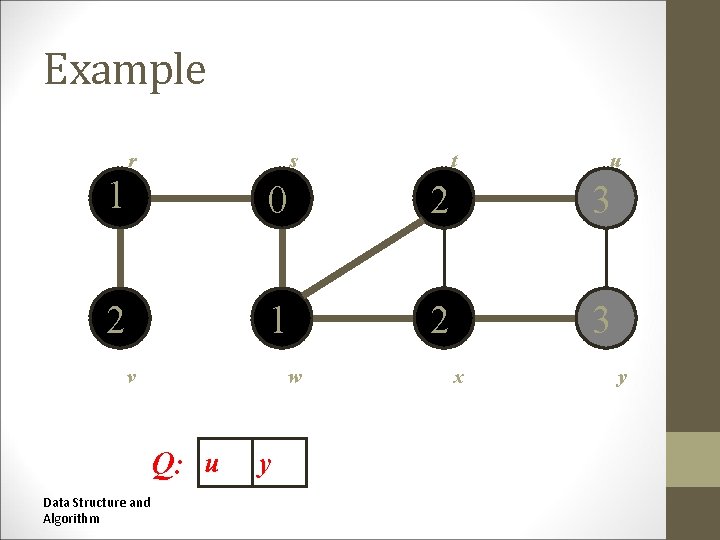
Example r s r t s t u u 1 0 2 2 1 2 v w w v Q: t Data Structure and Algorithm x x v x y y

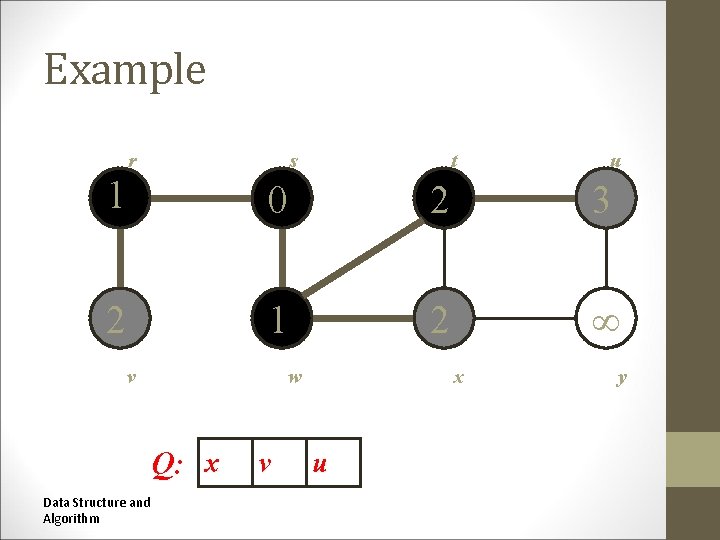
Example r s r t s t u u 1 0 2 3 2 1 2 v w w v Q: x Data Structure and Algorithm v x u x y y

Example r s r t s t u u 1 0 2 3 2 1 2 3 v w w v Q: v Data Structure and Algorithm u x y y

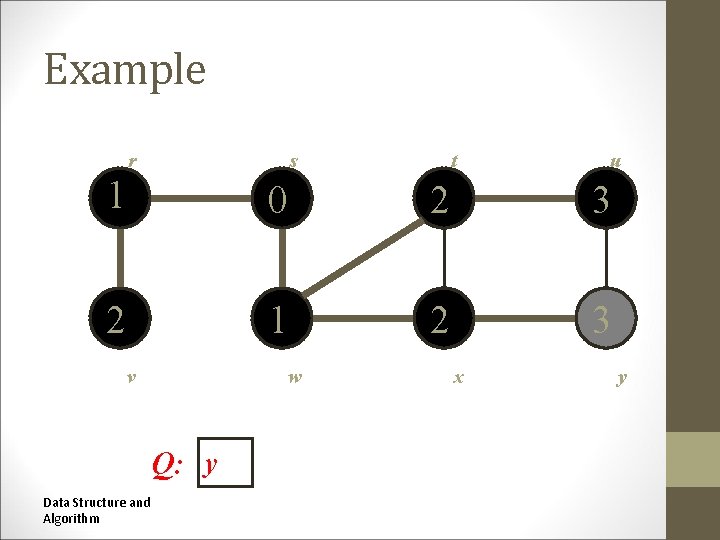
Example r s t t u u 1 0 2 3 2 1 2 3 v w w v Q: u Data Structure and Algorithm y x x y y

Example r s t t u u 1 0 2 3 2 1 2 3 v w w v Q: y Data Structure and Algorithm x x y y

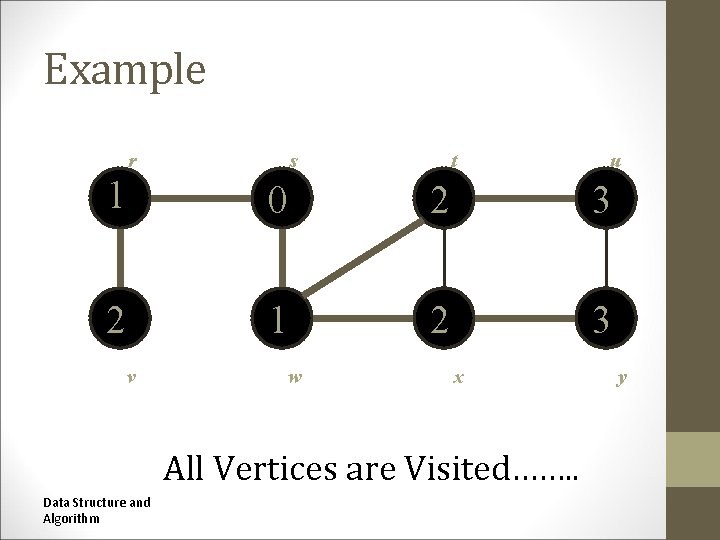
Example r s t t u u 1 0 2 3 2 1 2 3 v w w v x x Q: AllØVertices are Visited……. . Data Structure and Algorithm y y

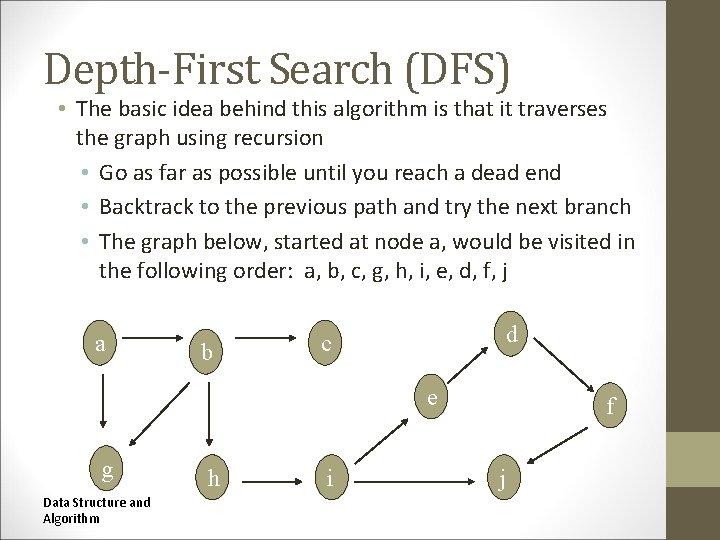
Depth-First Search (DFS) • The basic idea behind this algorithm is that it traverses the graph using recursion • Go as far as possible until you reach a dead end • Backtrack to the previous path and try the next branch • The graph below, started at node a, would be visited in the following order: a, b, c, g, h, i, e, d, f, j a b d c e g Data Structure and Algorithm h i f j

Depth-First Search depth. First. Search(v) { Label vertex v as reached. for (each unreached vertex u adjacenct from v) depth. First. Search(u); }

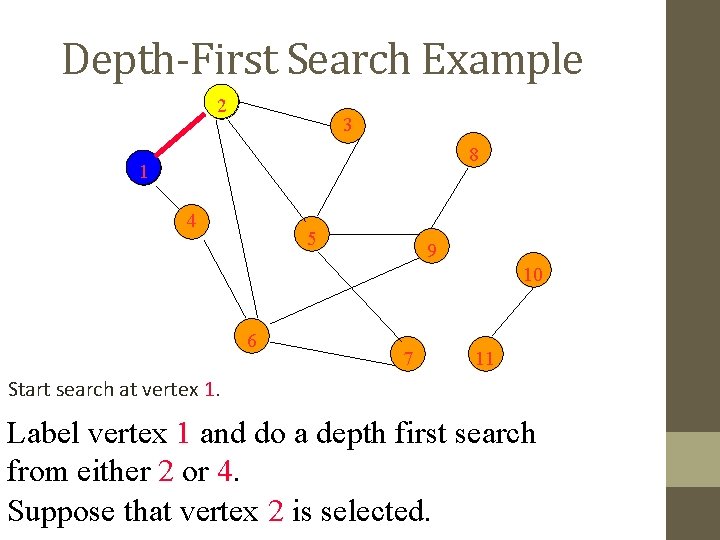
Depth-First Search Example 2 3 8 1 4 5 9 10 6 7 11 Start search at vertex 1. Label vertex 1 and do a depth first search from either 2 or 4. Suppose that vertex 2 is selected.

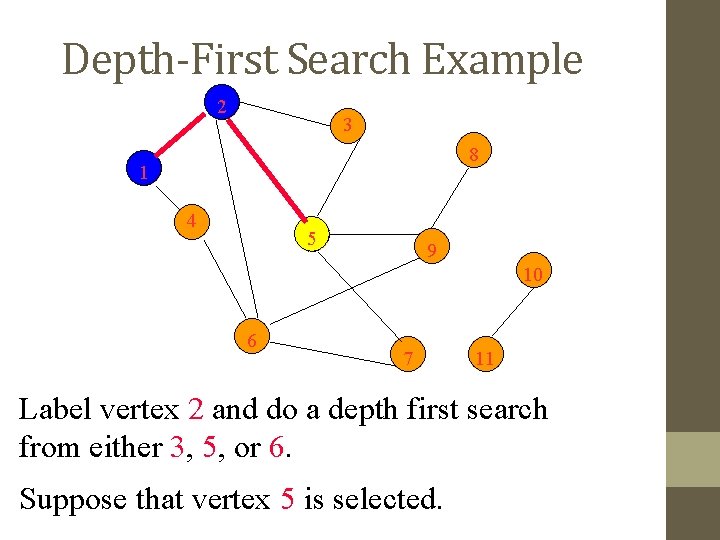
Depth-First Search Example 2 3 8 1 4 5 9 10 6 7 11 Label vertex 2 and do a depth first search from either 3, 5, or 6. Suppose that vertex 5 is selected.

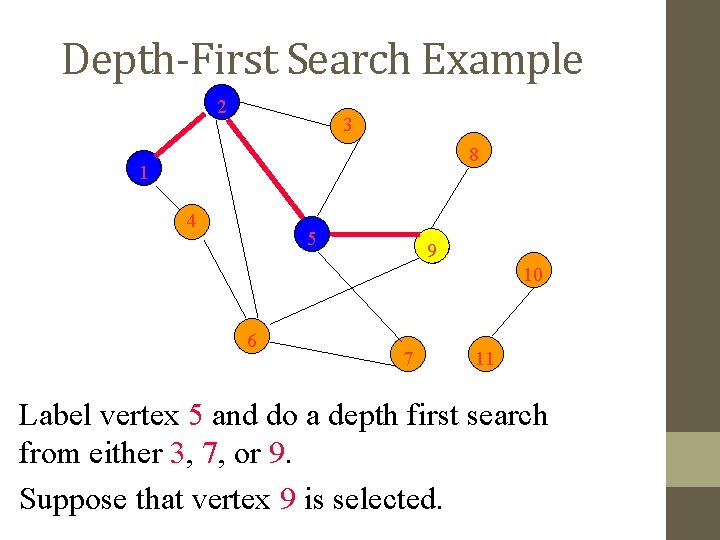
Depth-First Search Example 2 3 8 1 4 5 9 10 6 7 11 Label vertex 5 and do a depth first search from either 3, 7, or 9. Suppose that vertex 9 is selected.

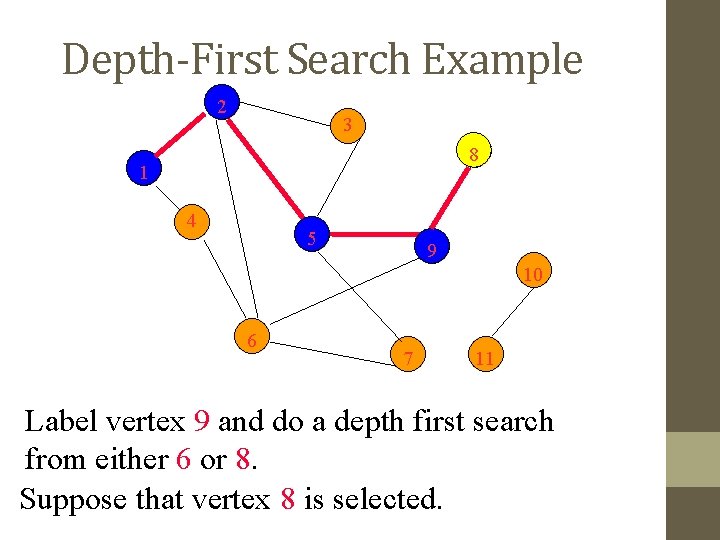
Depth-First Search Example 2 3 8 1 4 5 9 10 6 7 11 Label vertex 9 and do a depth first search from either 6 or 8. Suppose that vertex 8 is selected.

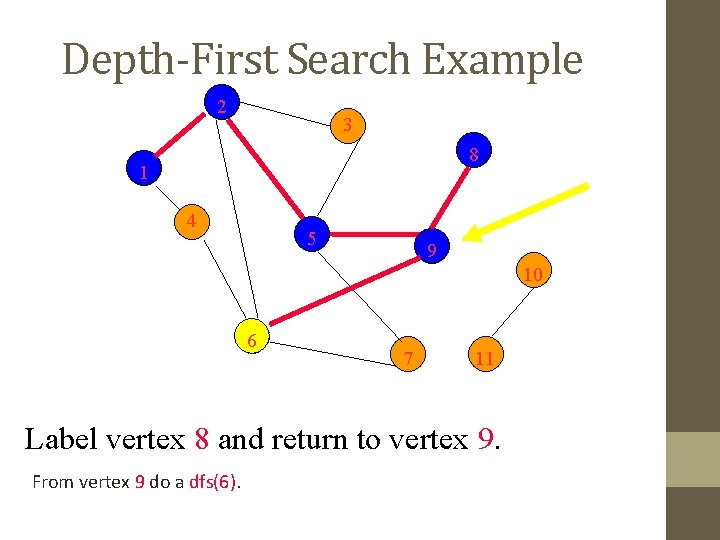
Depth-First Search Example 2 3 8 1 4 5 9 10 6 7 11 Label vertex 8 and return to vertex 9. From vertex 9 do a dfs(6).

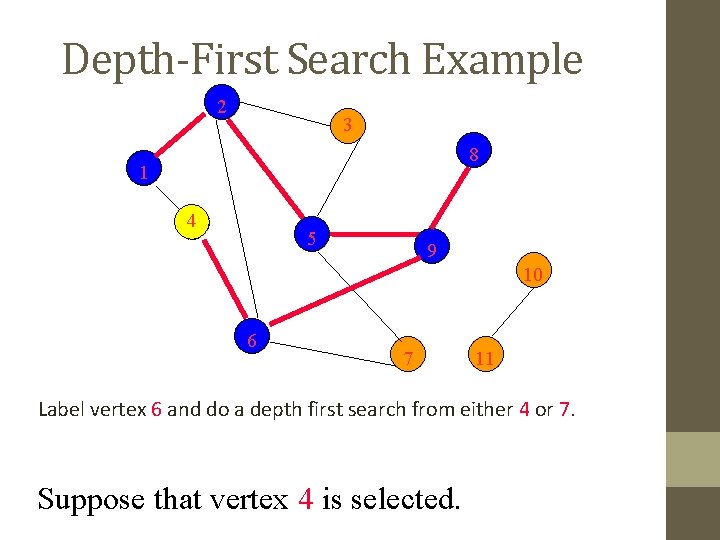
Depth-First Search Example 2 3 8 1 4 5 9 10 6 7 11 Label vertex 6 and do a depth first search from either 4 or 7. Suppose that vertex 4 is selected.

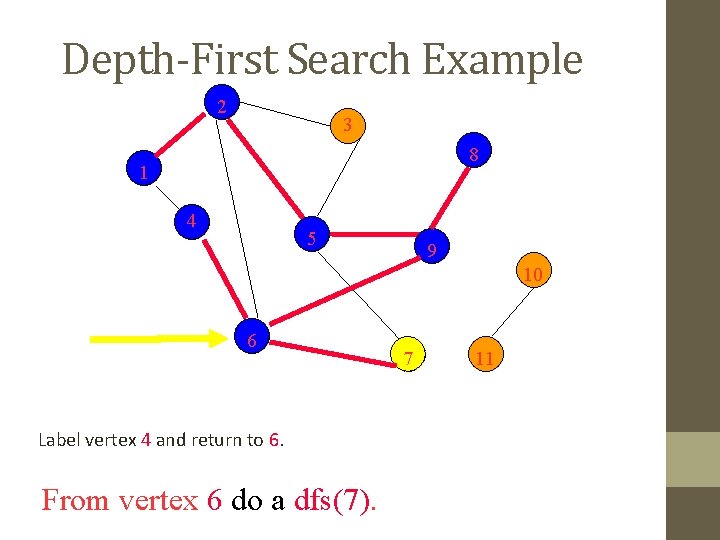
Depth-First Search Example 2 3 8 1 4 5 9 10 6 Label vertex 4 and return to 6. From vertex 6 do a dfs(7). 7 11

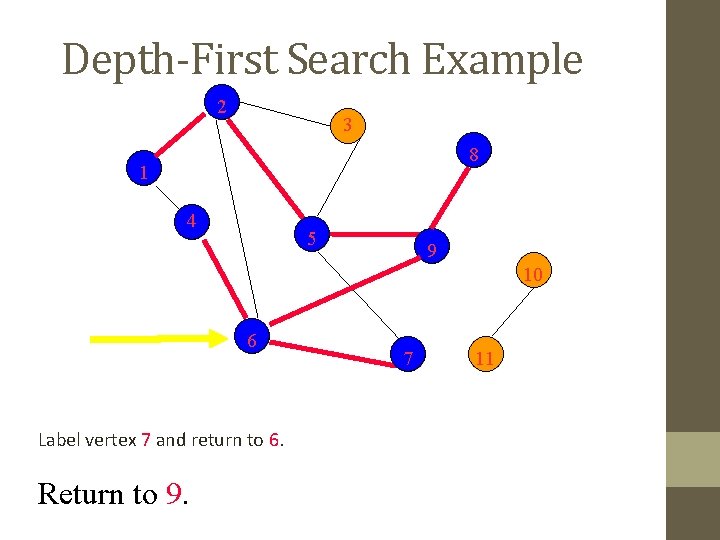
Depth-First Search Example 2 3 8 1 4 5 9 10 6 Label vertex 7 and return to 6. Return to 9. 7 11

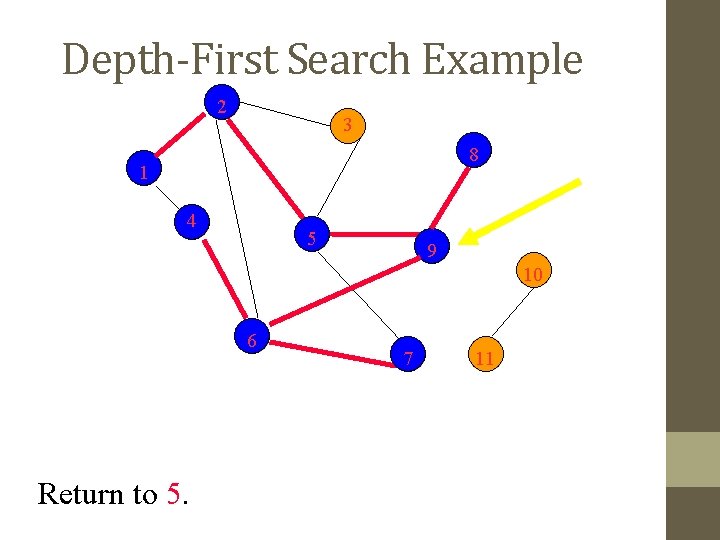
Depth-First Search Example 2 3 8 1 4 5 9 10 6 Return to 5. 7 11

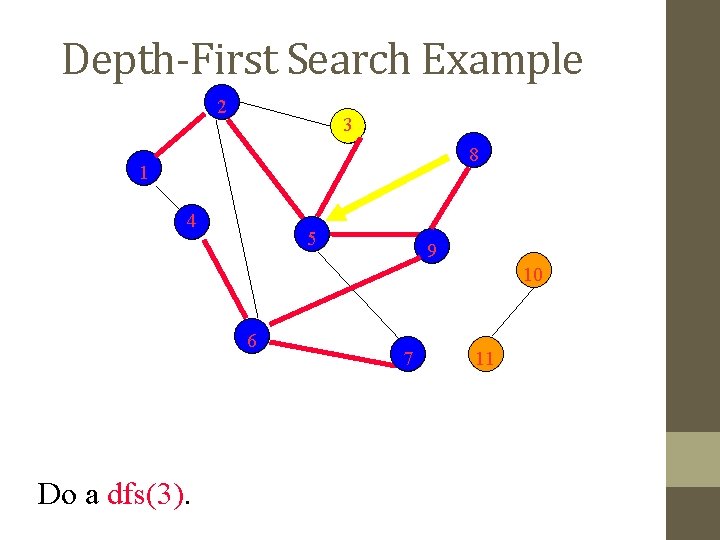
Depth-First Search Example 2 3 8 1 4 5 9 10 6 Do a dfs(3). 7 11

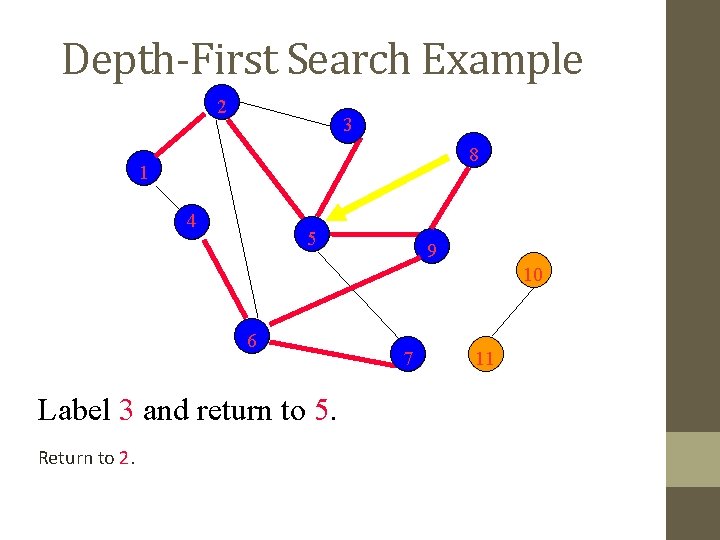
Depth-First Search Example 2 3 8 1 4 5 9 10 6 Label 3 and return to 5. Return to 2. 7 11

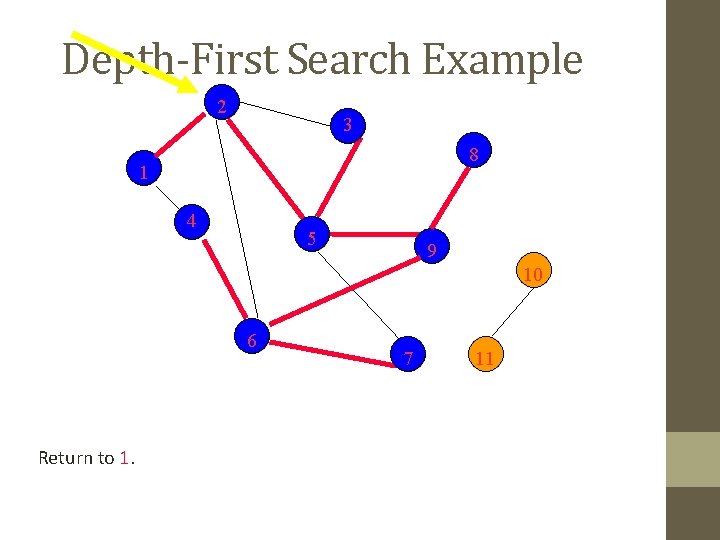
Depth-First Search Example 2 3 8 1 4 5 9 10 6 Return to 1. 7 11

Depth-First Search Example 2 3 8 1 4 5 9 10 6 7 11 Return to invoking method. For more detail contact us