DivideandConquer The mostwell known algorithm design strategy 1

Divide-and-Conquer The most-well known algorithm design strategy: 1. Divide instance of problem into two or more smaller instances 2. Solve smaller instances recursively 3. Obtain solution to original (larger) instance by combining these solutions Distinction between divide and conquer and decrease and conquer is somewhat vague. Dec/con typically does not solve both subproblems. A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 1

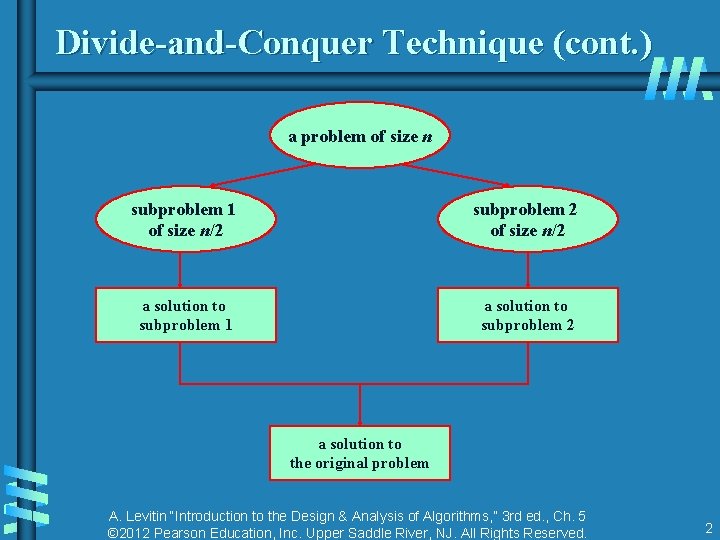
Divide-and-Conquer Technique (cont. ) a problem of size n subproblem 1 of size n/2 subproblem 2 of size n/2 a solution to subproblem 1 a solution to subproblem 2 a solution to the original problem A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 2

Divide-and-Conquer Examples b Sorting: mergesort and quicksort b Binary tree traversals b Multiplication of large integers b Matrix multiplication: Strassen’s algorithm b Closest-pair and convex-hull algorithms b Binary search: decrease-by-half (or degenerate divide&conq. ) A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 3

General Divide-and-Conquer Recurrence T(n) = a. T(n/b) + f (n) where f(n) (nd), d 0 Master Theorem: If a < bd, T(n) (nd) If a = bd, T(n) (nd log n) If a > bd, T(n) (nlog b a ) Note: The same results hold with O instead of . Examples: T(n) = 4 T(n/2) + n 2 T(n) = 4 T(n/2) + n 3 T (n ) ? A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 4

Mergesort Example A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 5

Mergesort b b b Split array A[0. . n-1] in two about equal halves and make copies of each half in arrays B and C Sort arrays B and C recursively Merge sorted arrays B and C into array A as follows: • Repeat the following until no elements remain in one of the arrays: – compare the first elements in the remaining unprocessed portions of the arrays – copy the smaller of the two into A, while incrementing the index indicating the unprocessed portion of that array • Once all elements in one of the arrays are processed, copy the remaining unprocessed elements from the other array into A. A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 6

Pseudocode of Mergesort Thinking about recursive programs: Assume recursive calls work and ask does the whole program then work? A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 7

Pseudocode of Merge A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 8

Analysis of Mergesort b Number of key comparisons – recurrence: C (n ) = … For merge step: C’(n) = … A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 9

Analysis of Mergesort b Number of key comparisons – recurrence: C(n) = 2 C(n/2) + C’(n) = 2 C(n/2) + n-1 For merge step – worst case: C’(n) = n-1 b How to solve? b Number of calls? Number of active calls? A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 10

General Divide-and-Conquer Recurrence T(n) = a. T(n/b) + f (n) where f(n) (nd), d 0 Master Theorem: If a < bd, T(n) (nd) If a = bd, T(n) (nd log n) If a > bd, T(n) (nlog b a ) Using log – Take log b of both sides: Case 1: logb a < d, T(n) (nd) Case 2: logb a = d, T(n) (nd logb n) Case 3: logb a > d, T(n) (nlog b a ) A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 11

Analysis of Mergesort b b b All cases have same efficiency: Θ(n log n) Number of comparisons in the worst case is close to theoretical minimum for comparison-based sorting: - Theoretical min: log 2 n! ≈ n log 2 n - 1. 44 n Space requirement: • Book’s algorithm? A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 12

Analysis of Mergesort b b b All cases have same efficiency: Θ(n log n) Number of comparisons in the worst case is close to theoretical minimum for comparison-based sorting: - Theoretical min: log 2 n! ≈ n log 2 n - 1. 44 n Space requirement: • Book’s algorithm: n + n Sum(1+1/2+1/4+…) = n + n Θ(2)= Θ(3 n) • Can be done Θ(2 n) : Don’t copy in sort; just specify bounds, copy into extra array on merge, then copy back – Any other space required? • Can be implemented in place. How … b Can be implemented without recursion (bottom-up) A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 13

Mergesort Example A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 14

Quicksort b b Select a pivot (partitioning element) – here, the first element Rearrange the list so that all the elements in the first s positions are smaller than or equal to the pivot and all the elements in the remaining n-s positions are larger than or equal to the pivot (see next slide for an algorithm) p A[i] p b b A[i] p Exchange the pivot with the last element in the first (i. e. , ) subarray — the pivot is now in its final position Sort the two subarrays recursively A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 15

Quicksort Algorithm QS (A, l, r) if l < r then s = partition (A, l, r) QS (A, , ) A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 16

Quicksort Algorithm QS (A, l, r) if l < r then s = partition (A, l, r) QS (A, l , s-1) QS (A, s+1, r ) Ask later: What if we skip final swap and use simpler bounds for first recursive call? A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 17

Hoare’s (Two-way) Partition Algorithm A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 18

Quicksort Example 5 3 1 9 8 2 4 7 A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 19

Quicksort Recursion Tree 0 1 2 3 4 5 6 7 5 3 1 9 8 2 4 7 0. . 7 / s=4 0. . 3 / s=x 0. . s-1 / s=? s+1. . 3 5. . 7 / s=y 5. . y-1 / s=? y+1. . 7 / s=? A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 20

Analysis of Quicksort Recurrences: b Best case: b Worst case: b Average case: Performance: b Best case: b Worst case: b Average case: A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 21

Analysis of Quicksort Recurrences: b Best case: T(n) = T(n/2) + Θ (n) b Worst case: T(n) = T(n-1) + Θ (n) b Average case: Performance: b Best case: b Worst case: b Average case: A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 22

Analysis of Quicksort Recurrences: b Best case: T(n) = T(n/2) + Θ (n) b Worst case: T(n) = T(n-1) + Θ (n) b Average case: Performance: b Best case: split in the middle — Θ(n log n) b Worst case: sorted array! — Θ(n 2) b Average case: random arrays — Θ(n log n) A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 23

Analysis of Quicksort b Problems: • Duplicate elements b Improvements: • better pivot selection: median of three partitioning • switch to insertion sort on small sub-arrays • elimination of recursion – How? These combine to 20 -25% improvement b Improvements: Dual Pivot b Method of choice for internal sorting of large files (n ≥ 10000) A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 24

Binary Tree Algorithms Binary tree is a divide-and-conquer ready structure! Ex. 1: Classic traversals (preorder, inorder, postorder) Algorithm Inorder(T) a a b c d b e c e d Efficiency: Θ(n) A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 25

Binary Tree Algorithms Binary tree is a divide-and-conquer ready structure! Ex. 1: Classic traversals (preorder, inorder, postorder) Algorithm Inorder(T) if T Inorder(Tleft) print(root of T) Inorder(Tright) a b a c d b e c e d Efficiency: Θ(n) A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 26

Binary Tree Algorithms (cont. ) Ex. 2: Computing the height of a binary tree h(T) = ? ? Efficiency: Θ(n) A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 27

Binary Tree Algorithms (cont. ) Ex. 2: Computing the height of a binary tree h(T) = max{h(TL), h(TR)} + 1 if T and h( ) = -1 Efficiency: Θ(n) A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 28

Multiplication of Large Integers Consider the problem of multiplying two (large) n-digit integers represented by arrays of their digits such as: A = 12345678901357986429 B = 87654321284820912836 The grade-school algorithm: a 1 a 2 … an b 1 b 2 … bn (d 10) d 11 d 12 … d 1 n (d 20) d 21 d 22 … d 2 n ………………… (dn 0) dn 1 dn 2 … dnn Efficiency: ? ? one-digit multiplications A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 29

Multiplication of Large Integers Consider the problem of multiplying two (large) n-digit integers represented by arrays of their digits such as: A = 12345678901357986429 B = 87654321284820912836 The grade-school algorithm: a 1 a 2 … an b 1 b 2 … bn (d 10) d 11 d 12 … d 1 n (d 20) d 21 d 22 … d 2 n ………………… (dn 0) dn 1 dn 2 … dnn Efficiency: n 2 one-digit multiplications A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 30

First Divide-and-Conquer Algorithm A small example: A B where A = 2135 and B = 4014 A = (21· 102 + 35), B = (40 · 102 + 14) So, A B = (21 · 102 + 35) (40 · 102 + 14) = 21 40 · 104 + (21 14 + 35 40) · 102 + 35 14 In general, if A = A 1 A 2 and B = B 1 B 2 (where A and B are n-digit, and A 1, A 2, B 1, B 2 are n / 2 -digit numbers), A B = A 1 B 1· 10 n + (A 1 B 2 + A 2 B 1) · 10 n/2 + A 2 B 2 Recurrence for the number of one-digit multiplications M(n): M(n) = 4 M(n/2), M(1) = 1 Solution: M(n) = n 2 A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 31

Second Divide-and-Conquer Algorithm A B = A 1 B 1· 10 n + (A 1 B 2 + A 2 B 1) · 10 n/2 + A 2 B 2 The idea is to decrease the number of multiplications from 4 to 3: (A 1 + A 2 ) (B 1 + B 2 ) = A 1 B 1 + (A 1 B 2 + A 2 B 1) + A 2 B 2, I. e. , (A 1 B 2 + A 2 B 1) = (A 1 + A 2 ) (B 1 + B 2 ) - A 1 B 1 - A 2 B 2, which requires only 3 multiplications at the expense of (4 -1=3) extra additions and subtractions (2 adds and 2 subs – 1 add) Recurrence for the number of multiplications M(n): M(n) = 3 M(n/2), M(1) = 1 Solution: M(n) = 3 log 2 n = nlog 23 ≈ n 1. 585 A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 32

Example of Large-Integer Multiplication 2135 4014 A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 33

Strassen’s Matrix Multiplication Strassen observed [1969] that the product of two matrices can be computed as follows: C 00 C 01 A 00 A 01 = C 10 C 11 B 00 B 01 * A 10 A 11 B 10 B 11 M 1 + M 4 - M 5 + M 7 M 3 + M 5 = M 2 + M 4 b b M 1 + M 3 - M 2 + M 6 Example: M 2 + M 4 = (A 10 + A 11) B 00 + A 11 (B 10 - B 00) = A 10 B 00 + A 11 B 10 A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 34

Formulas for Strassen’s Algorithm M 1 = (A 00 + A 11) (B 00 + B 11) M 2 = (A 10 + A 11) B 00 M 3 = A 00 (B 01 - B 11) M 4 = A 11 (B 10 - B 00) M 5 = (A 00 + A 01) B 11 M 6 = (A 10 - A 00) (B 00 + B 01) M 7 = (A 01 - A 11) (B 10 + B 11) A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 35

Analysis of Strassen’s Algorithm If n is not a power of 2, matrices can be padded with zeros. Number of multiplications: M(n) = 7 M(n/2), M(1) = 1 Solution: M(n) = 7 log 2 n = nlog 27 ≈ n 2. 807 vs. n 3 of brute-force alg. Algorithms with better asymptotic efficiency are known but they are even more complex. A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 36

Closest-Pair Problem by Divide-and-Conquer Step 1 Divide the points given into two subsets Pl and Pr by a vertical line x = m so that half the points lie to the left or on the line and half the points lie to the right or on the line. A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 37

Closest-Pair Driver b b b CP_Driver(A) Pre => A(1. . n), n > 1, is an array of (X, Y), pairs Post => Returns distance between closest pair in A b P(1. . n) : = Copy of A, sorted by X Q(1. . n) : = Copy of A, sorted by Y b return CP(P, Q) b A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 38

Closest-Pair Problem by Divide-and-Conquer b • • • • CP(P, Q) – Pre=> P (1. . n) and Q (1. . n) have same points, P is x-sorted, Q y-sorted If n <= 3 then return CPBF(P) Copy P(1. . n/2) into PL(1. . n/2) Distribute-copy the same n/2 points from Q into QL (anti-merge) Copy P(n/2+1. . n) into PR(1. . n/2) Distribute-copy the same n/2 points from Q into QR !! Careful d. L : = CP(PL, QL); d. R : = CP(PR, QR) d : = min(d. L, d. R); dsq : = d ** 2 midx = P(n/2). x strip(1. . num) => strip(i) : = Q(k) iff | Q(k). x – midx | <= d For i in 1. . Num – 1 loop k : = i + 1 while k <= num and (strip(i). y – strip(k). y)**2 < dsq loop dsq : = min (dsq, (strip(i). x – strip(k). x)**2 + (strip(i). y – strip(k). y)**2) k : = k + 1 return sqrt(dsq) A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 39

CP Notes b • • • • CP(P, Q) – Pre=>P and Q have same points, P x sorted, Q y sorted y, P(1. . n), n> 1 Copy P(1. . n/2) into PL(1. . n/2) and same n/2 points from Q into QL Copy P(n/2+1. . n) into PR(1. . n/2)and same n/2 points from Q into QR -- Divide Q based on Q(i). x < P(n/2). x. if Q(k). x = P(n/2). x must send to correct side -- N. B. P and Q are sorted. PL, PR, QL, QR are distributed, not resorted. d. L : = CP(PL, QL); d. R : = CP(PR, QR) d : = min(d. L, d. R) ; dsq : = d** 2 -- For efficiency midx = P(n/2). x -- x value of middle point strip(1. . num) => strip(i) : = Q(k) iff | Q(k). x – midx | <= d -- Copy points of Q within distance d of middle into strip. Num such points. For i in 1. . Num – 1 loop k : = i + 1 while k <= num and (strip(i). y – strip(k). y)**2 < dsq loop dsq : = min (dsq, (strip(i). x – strip(k). x)**2 + (strip(i). y – strip(k). y)**2) k : = k + 1 return sqrt(dsq) -- CP can add sorted P index to points of Q, simplifying distribution! A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 40

CP Assignment: Performance Measurement b • • • • CP(P, Q) – Pre=>P and Q have same points, P x sorted, Q y sorted y, P(1. . n), n> 1 -- Count number of calls here, using a GLOBAL VARIABLE Copy P(1. . n/2) into PL(1. . n/2) and same n/2 points from Q into QL Copy P(n/2+1. . n) into PR(1. . n/2)and same n/2 points from Q into QR d. L : = CP(PL, QL); d. R : = CP(PR, QR) d : = min(d. L, d. R) ; dsq : = d** 2 midx = P(n/2). x strip(1. . num) => strip(i) : = Q(k) iff | Q(k). x – midx | <= d For i in 1. . Num – 1 loop k : = i + 1 while k <= num and (strip(i). y – strip(k). y)**2 < dsq loop -- Count number of distance calculations here, using a global dsq : = min (dsq, (strip(i). x – strip(k). x)**2 + (strip(i). y – strip(k). y)**2) k : = k + 1 return sqrt(dsq) A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 41

Closest Pair by Divide-and-Conquer (cont. ) Step 2 Find recursively the closest pairs for the left and right subsets. Step 3 Set d = min{dl, dr} We can limit our attention to the points in the symmetric vertical strip S of width 2 d as possible closest pair. (The points are stored and processed in increasing order of their y coordinates. ) Step 4 Scan the points in the vertical strip S from the lowest up. For every point p(x, y) in the strip, inspect points in in the strip that may be closer to p than d. There can be no more than 5 such points following p on the strip list! A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 42

Closest Pair by Divide-and-Conquer (cont. ) How many points could be in each strip? n/2 Brute force would look at all n/2 x n/2 pairs Why can we restrict ourselves to calculating the distance from each point to the next 5 points Because only the next 5 points could be within distance d of the current point. Why? Consider a square of size d: No two points in it can be closer than d. How many points can it contain. No more than 4 (since 5 won’t fit). Thus a rectangle of size dx 2 d can only contain 8 points (or 6 if duplicates are not allowed). So from a point, only check the next 7 (or 5) points. A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 43

Efficiency of the Closest-Pair Algorithm Running time of the algorithm is described by T(n) = 2 T(n/2) + M(n), where M(n) O(n) By the Master Theorem (with a = 2, b = 2, d = 1) T(n) O(n log n) A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 44

Quickhull Algorithm Convex hull: smallest convex set that includes given points b Assume points are sorted by x-coordinate values b Identify extreme points P 1 and P 2 (leftmost and rightmost) b Compute upper hull recursively: • • • b find point Pmax that is farthest away from line P 1 P 2 compute the upper hull of the points to the left of line P 1 Pmax compute the upper hull of the points to the left of line Pmax. P 2 Compute lower hull in a similar manner Pmax P 2 P 1 A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 45

Efficiency of Quickhull Algorithm b b Finding point farthest away from line P 1 P 2 can be done in linear time Time efficiency: • Assume nu and nl points in upper and lower hulls • Performance: T(n) = T(? ) + Θ(? ) • Worst case: T(n) = T(? ) + Θ(? ) • Expected case: T(n) = T(? ) + Θ(? ) A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 46

Efficiency of Quickhull Algorithm b b Finding point farthest away from line P 1 P 2 can be done in linear time Time efficiency: • Assume nu and nl points in upper and lower hulls • Performance: T(n) = T(nu) + T(nl) + Θ(n) • Worst case: T(n) = T(1) + T(n-1) + Θ n) = ? • Expected case: T(n) = T(n/2) + Θ(n) = ? A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 47

Efficiency of Quickhull Algorithm b b Finding point farthest away from line P 1 P 2 can be done in linear time Time efficiency: • Assume nu and nl points in upper and lower hulls • Performance: T(n) = T(nu) + T(nl) + Θ(n) • Worst case: T(n) = T(1) + T(n-1) + Θ(n) = Θ(n^2) • Expected case: T(n) = T(n/2) + Θ(n) = Θ(n lg n) Can we do better? A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 48

Efficiency of Quickhull Algorithm b Finding point farthest from line P 1 P 2 can be done in Θ(n) b Time efficiency: • Assume nu and nl points in upper and lower hulls • Performance: T(n) = T(nu) + T(nl) + Θ(n) • Worst case: T(n) = T(1) + T(n-1) + Θ(n) = Θ(n^2) • Expected case: T(n) = T(n/2) + Θ(n) = Θ(n lg n) Can we do better? T(n) = T(n/4) + Θ(n) = Θ(n) A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 49

Efficiency of Quickhull Algorithm b Finding point farthest from line P 1 P 2 can be done in Θ(n) b Time efficiency: • worst case: Θ(n 2) (as quicksort) • average case: Θ(n lg n) or Θ(n) (assuming reasonable distribution of points) b If points are not initially sorted by x-coordinate value, this can be accomplished in O(n log n) time b Several O(n log n) algorithms for convex hull are known Field is called Computational Geometry b A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All Rights Reserved. 50