Divide and Conquer The most well known algorithm



![Mergesort Algorithm: b Split array A[1. . n] in two and make copies of Mergesort Algorithm: b Split array A[1. . n] in two and make copies of](https://slidetodoc.com/presentation_image_h/16374d27129376d4a7fd2fe50497b704/image-5.jpg)













![Strassen’s matrix multiplication b Strassen observed [1969] that the product of two matrices A Strassen’s matrix multiplication b Strassen observed [1969] that the product of two matrices A](https://slidetodoc.com/presentation_image_h/16374d27129376d4a7fd2fe50497b704/image-19.jpg)


- Slides: 21

Divide and Conquer The most well known algorithm design strategy: 1. Divide instance of problem into two or more smaller instances 2. Solve smaller instances recursively 3. Obtain solution to original (larger) instance by combining these solutions Design and Analysis of Algorithms - Chapter 4 1

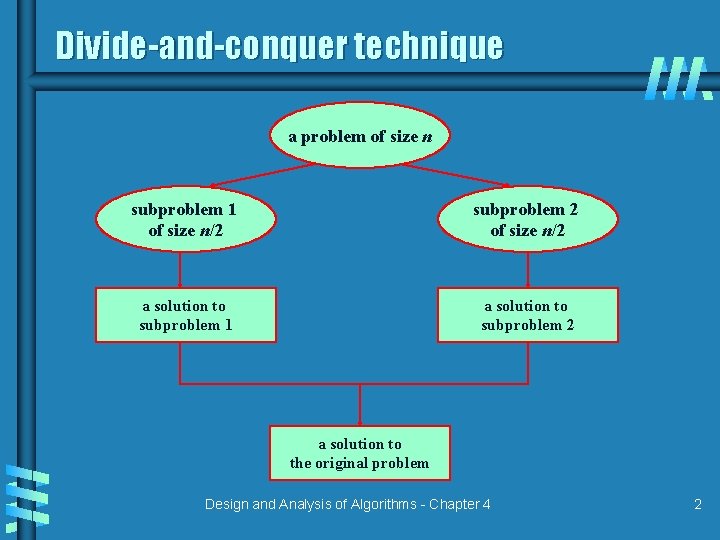
Divide-and-conquer technique a problem of size n subproblem 1 of size n/2 subproblem 2 of size n/2 a solution to subproblem 1 a solution to subproblem 2 a solution to the original problem Design and Analysis of Algorithms - Chapter 4 2

Divide and Conquer Examples b b b Sorting: mergesort and quicksort Tree traversals Binary search Matrix multiplication - Strassen’s algorithm Convex hull - Quick. Hull algorithm Design and Analysis of Algorithms - Chapter 4 3

General Divide and Conquer recurrence: T(n) = a. T(n/b) + f (n) 1. 2. 3. a < bk a = bk a > bk where f (n) ∈ Θ(nk) T(n) ∈ Θ(nk lg n ) T(n) ∈ Θ(nlog b a) Note: the same results hold with O instead of Θ. Design and Analysis of Algorithms - Chapter 4 4
![Mergesort Algorithm b Split array A1 n in two and make copies of Mergesort Algorithm: b Split array A[1. . n] in two and make copies of](https://slidetodoc.com/presentation_image_h/16374d27129376d4a7fd2fe50497b704/image-5.jpg)
Mergesort Algorithm: b Split array A[1. . n] in two and make copies of each half in arrays B[1. . n/2 ] and C[1. . n/2 ] b Sort arrays B and C b Merge sorted arrays B and C into array A as follows: • Repeat until no elements remain in one of the arrays: – compare the first elements in the remaining unprocessed portions of the arrays – copy the smaller of the two into A, while incrementing the index indicating the unprocessed portion of that array • Once all elements in one of the arrays are processed, copy the remaining unprocessed elements from the other array into A. Design and Analysis of Algorithms - Chapter 4 5

Mergesort Example 7 2 1 6 4 Design and Analysis of Algorithms - Chapter 4 6

Efficiency of mergesort b C(n) = 2 C(n/2) + Cmerge(n) for n>1, C(1)=0 b All cases have same efficiency: Θ(n log n) b Number of comparisons is close to theoretical minimum for comparison-based sorting: • log n ! ≈ n lg n - 1. 44 n b Space requirement: Θ(n) (NOT in-place) b Can be implemented without recursion (bottom-up) Design and Analysis of Algorithms - Chapter 4 7

Quicksort b Select a pivot (partitioning element) b Rearrange the list so that all the elements in the positions before the pivot are smaller than or equal to the pivot and those after the pivot are larger than the pivot (See algorithm Partition in section 4. 2) b Exchange the pivot with the last element in the first (i. e. , ≤ sublist) – the pivot is now in its final position b Sort the two sublists p A[i]≤p A[i]>p Design and Analysis of Algorithms - Chapter 4 8

The partition algorithm Design and Analysis of Algorithms - Chapter 4 9

Quicksort Example 15 22 13 27 12 10 20 25 Design and Analysis of Algorithms - Chapter 4 10

Efficiency of quicksort b Best case: split in the middle — Θ( n log n) b Worst case: sorted array! — Θ( n 2) b Average case: random arrays — Θ( n log n) b Improvements: • better pivot selection: median of three partitioning avoids worst case in sorted files • switch to insertion sort on small subfiles • elimination of recursion these combine to 20 -25% improvement b Considered the method of choice for internal sorting for large files (n ≥ 10000) Design and Analysis of Algorithms - Chapter 4 11

Multiplication of large integers b To multiply two integers of n 1 and n 2 digits by a pen-and-pencil algorithm, we perform n 1 n 2 multiplications b However, remark the example of 23*14, where 23=2. 101+3. 100 and 14=1. 101+4. 100 b In general: c=a*b=c 2. 10 n+c 1. 10 n/2+c 0. 100 where c 2=a 1*b 1, c 0=a 0*b 0, c 1=(a 1+a 0)*(b 1+b 0)-(c 2+c 0) a 0, a 1, b 0, b 1 be the left and right parts of a and b. b Recurrence relation b Efficiency Design and Analysis of Algorithms - Chapter 4 12

Closest Pair Problem b Problem: find closest points among n ones in k- dimensional space b Assume points are sorted by x-coordinate values b Divide the points in two subsets S 1 and S 2 of n/2 points by drawing a vertical line at x=c b Select the closest pair among the closest pair of the left subset (distance d 1), of the closest pair of the right subset (distance d 2), and the closest pair with points from both sides b We need to examine a stripe of width 2 d, where d=min[d 1, d 2] Design and Analysis of Algorithms - Chapter 4 13

Closest Pair Problem (2) b Geometric explanation b Recurrence relation T(n) = 2 T(n/2) + M(n) b Efficiency in O(n logn) b Optimality Design and Analysis of Algorithms - Chapter 4 14

Quick. Hull Algorithm Inspired by Quicksort compute Convex Hull: b Assume points are sorted by x-coordinate values b Identify extreme points P 1 and P 2 (part of hull) b The set S of points is divided in two subsets S 1 and S 2 b Compute Convex Hull for S 1 b Compute Convex Hull for S 2 in a similar manner Pmax P 2 P 1 Design and Analysis of Algorithms - Chapter 4 15

Quick. Hull Algorithm (2) b How to compute the Convex (upper) Hull for S 1 • find point Pmax that is farthest away from line P 1 P 2 • compute the hull of the points to the left of line P 1 Pmax • compute the hull of the points to the left of line Pmax. P 2 b How to find the Pmax point • Pmax maximizes the area of the triangle Pmax. P 1 P 2 • if tie, select the Pmax that maximizes the angle Pmax. P 1 P 2 b The points inside triangle Pmax. P 1 P 2 can be excluded from further consideration b How to find geometrically the point Pmax and the points to the left of line P 1 Pmax Design and Analysis of Algorithms - Chapter 4 16

Quick. Hull Algorithm (3) b How to find geometrically the point Pmax and the points to the left of line P 1 Pmax • Given points P 1(x 1, y 1), P 2(x 2, y 2), Pmax(xmax, ymax) • The area of the triangle is half of the magnitude of the determinant x 1 y 1 1 x 2 y 2 1 =x 1 y 2+xmaxy 1+x 2 ymax–xmaxy 2–x 2 y 1 -x 1 ymax xmax ymax 1 • The sign of the expression is positive if and only if the point Pmax is to the left of the line P 1 P 2 Design and Analysis of Algorithms - Chapter 4 17

Efficiency of Quick. Hull algorithm b Finding point farthest away from line P 1 P 2 can be done in linear time b This gives same efficiency as quicksort: • • Worst case: Θ(n 2) Average case: Θ(n log n) If points are not initially sorted by x-coordinate value, this can be accomplished in Θ(n log n) — no increase in asymptotic efficiency class b Other algorithms for convex hull: b • Graham’s scan • DCHull also in Θ(n log n) Design and Analysis of Algorithms - Chapter 4 18
![Strassens matrix multiplication b Strassen observed 1969 that the product of two matrices A Strassen’s matrix multiplication b Strassen observed [1969] that the product of two matrices A](https://slidetodoc.com/presentation_image_h/16374d27129376d4a7fd2fe50497b704/image-19.jpg)
Strassen’s matrix multiplication b Strassen observed [1969] that the product of two matrices A and B (of size 2 nx 2 n) can be computed as follows: C 00 C 01 A 00 A 01 = C 10 C 11 B 00 B 01 * A 10 A 11 B 10 B 11 M 1 + M 4 - M 5 + M 7 M 3 + M 5 = M 2 + M 4 M 1 + M 3 - M 2 + M 6 Design and Analysis of Algorithms - Chapter 4 19

Submatrices: b M 1 = (A 00 + A 11) * (B 00 + B 11) b M 2 = (A 10 + A 11) * B 00 b M 3 = A 00 * (B 01 - B 11) b M 4 = A 11 * (B 10 - B 00) b M 5 = (A 00 + A 01) * B 11 b M 6 = (A 10 - A 00) * (B 00 + B 01) b M 7 = (A 01 - A 11) * (B 10 + B 11) Design and Analysis of Algorithms - Chapter 4 20

Efficiency of Strassen’s algorithm b b b If n is not a power of 2, matrices can be padded with zeros Number of multiplications: Number of additions: Recurrence relations: Other algorithms have improved this result, but are even more complex Design and Analysis of Algorithms - Chapter 4 21