A and AO Search Algorithm Hananel Hazan Based

A* and AO* Search Algorithm Hananel Hazan Based on Prof. Larry Manevitz’s slides

Draughts (or checkers) דמקה https: //en. wikipedia. org/wiki/Freeciv https: //en. wikipedia. org/wiki/Draughts • In the 1950 s, Arthur Samuel created one of the first board gameplaying programs of any kind • in 2007 scientists at the University of Alberta[13] evolved their "Chinook" program up to the point where it is unbeatable. A brute force approach that took hundreds of computers working nearly 2 decades was used to solve the game, [14] showing that a game of draughts will always end in a stalemate if neither player makes a mistake. [15][16]

RPG situation
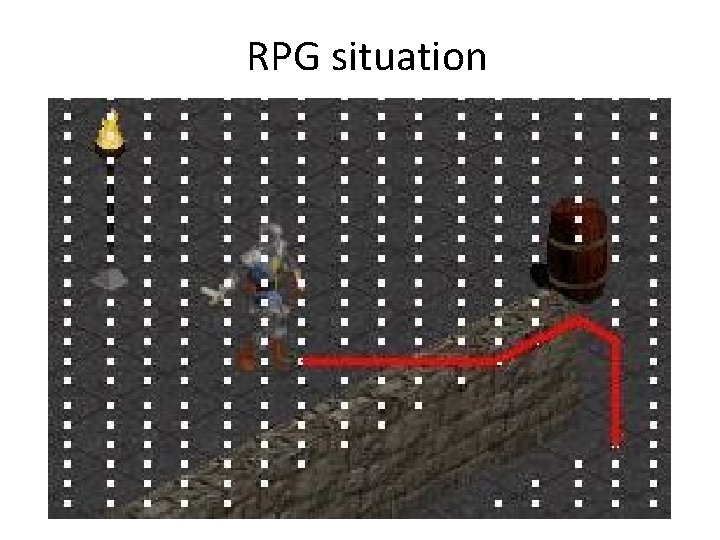
RPG situation


RPG situation






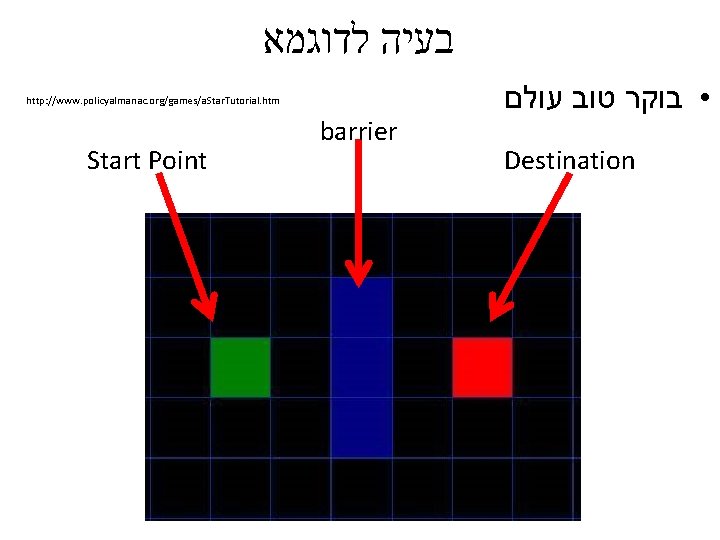
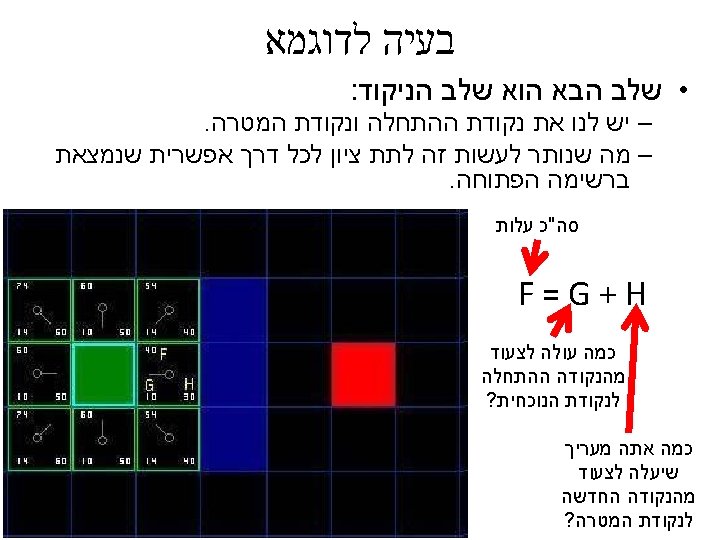
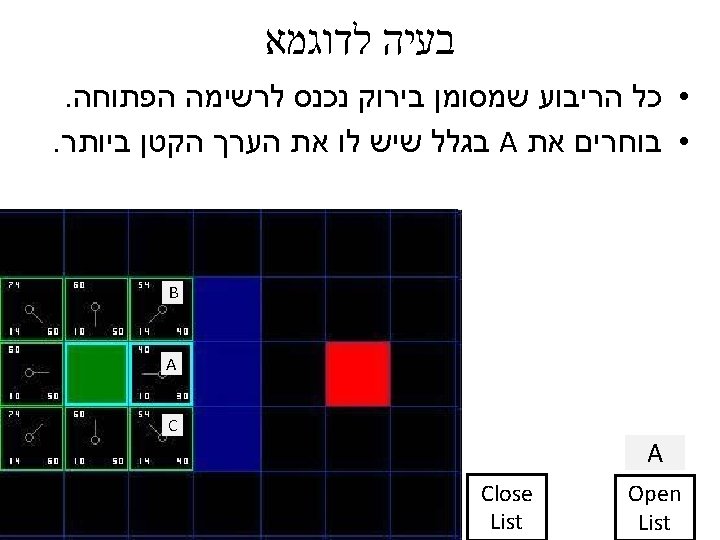
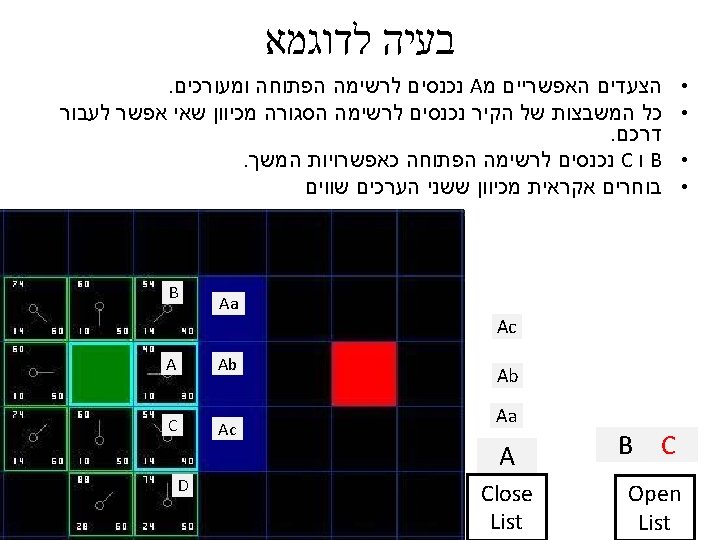
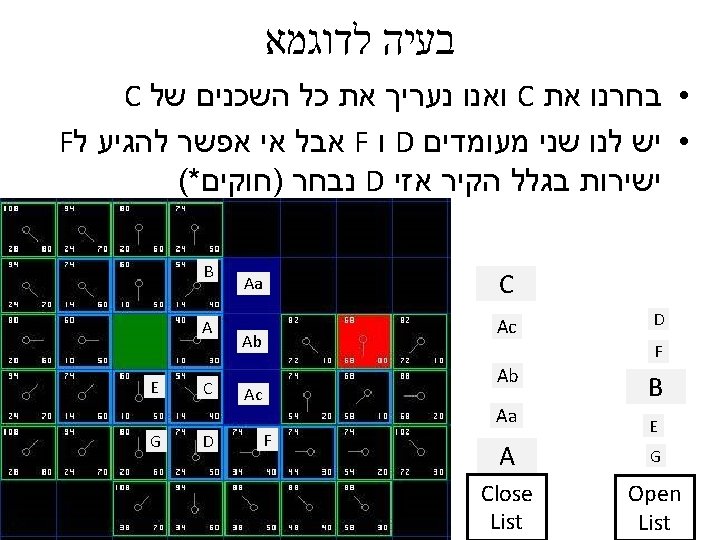
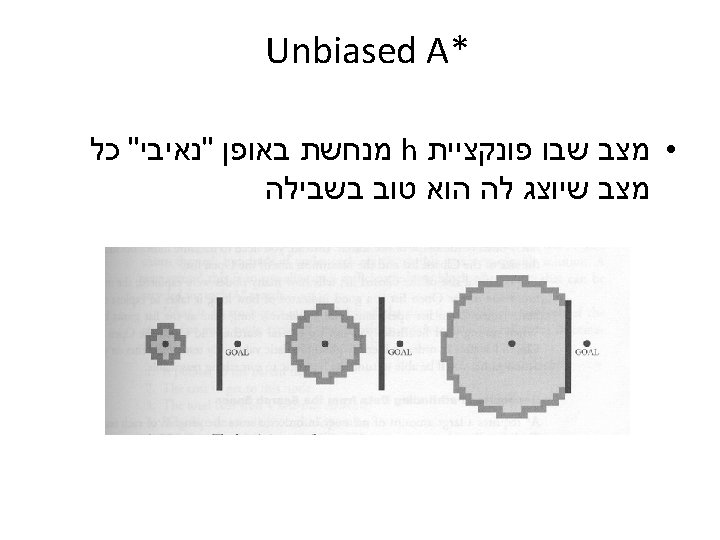
בעיה לדוגמא http: //www. policyalmanac. org/games/a. Star. Tutorial. htm Start Point barrier • בוקר טוב עולם Destination
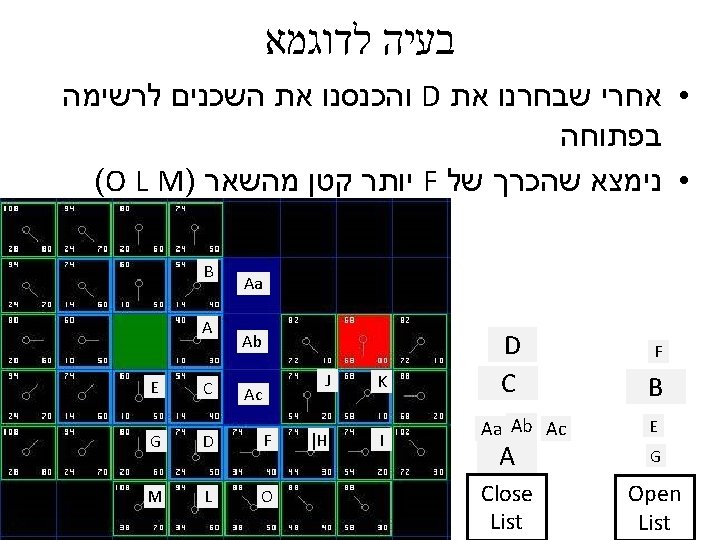
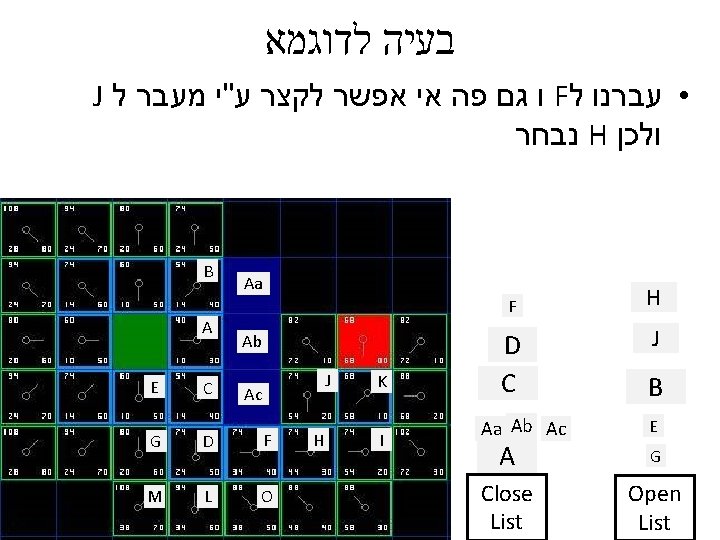
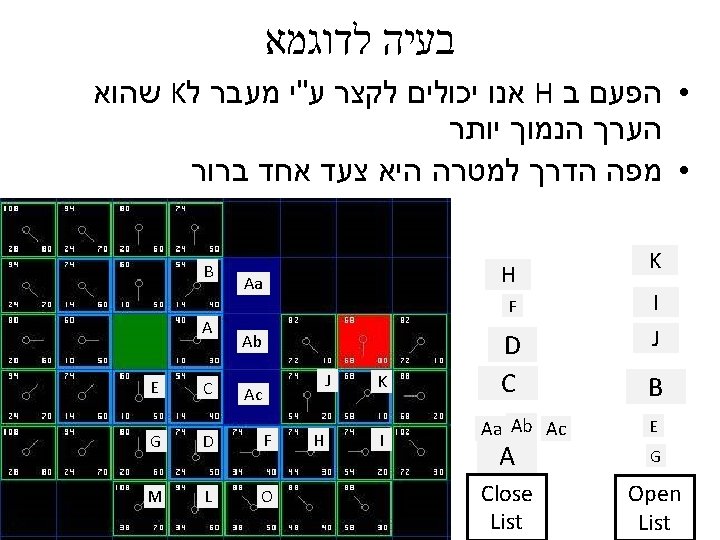
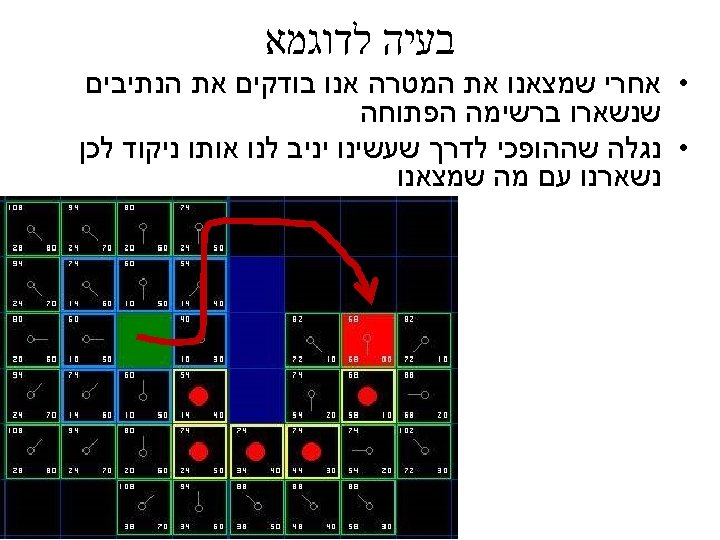
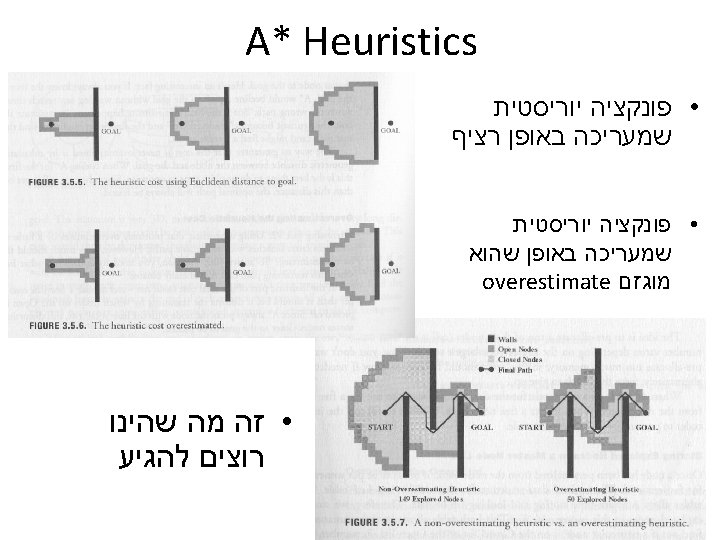



AO* (star) ? ?

What are difference between A and AO algorithm? • The main difference between the A*(A star) and AO*(AO star) algorithms is that A* algorithm is a OR graph algorithm and AO* is a AND-OR graph algorithm. • In OR graph algorithm it just find only one solution (i. e. either OR solution means this OR this). • But in the AND-OR graph algorithm it find more than one solution by ANDing two or more branches.
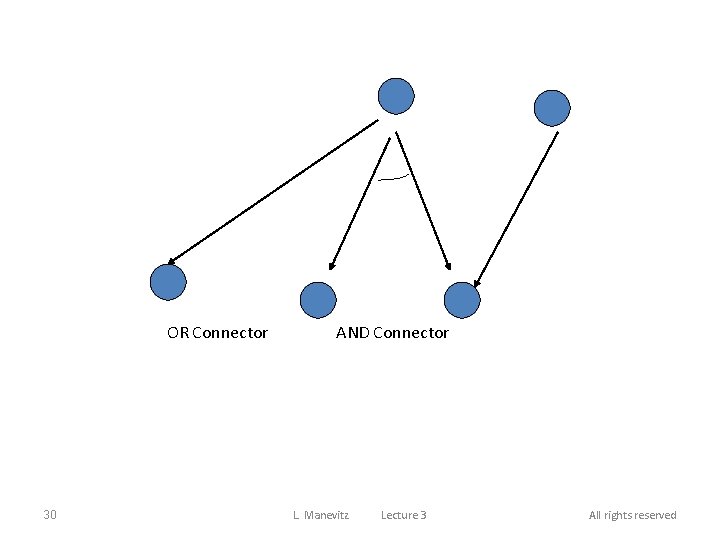
OR Connector 30 AND Connector L. Manevitz Lecture 3 All rights reserved

הנחות עבודה • Data Structure – Graph – Marked Connectors (down; unlike A*) – Costs q() maintained on nodes – SOLVED markings – Note: We’ll discuss on acyclic graphs.
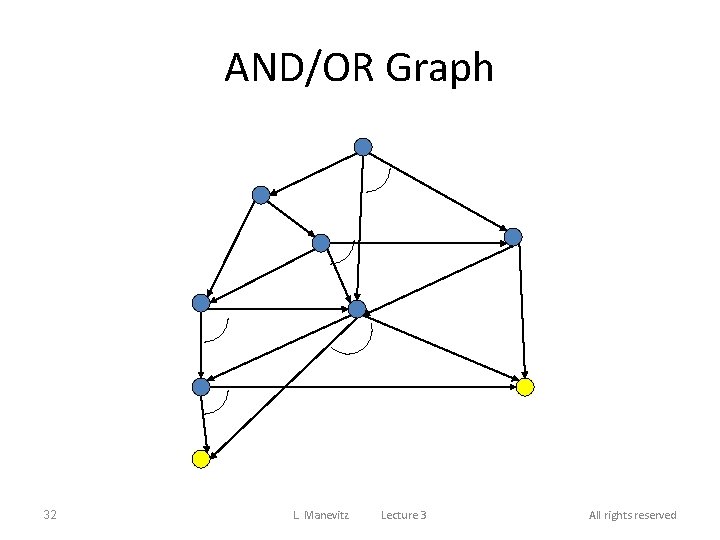
AND/OR Graph 32 L. Manevitz Lecture 3 All rights reserved
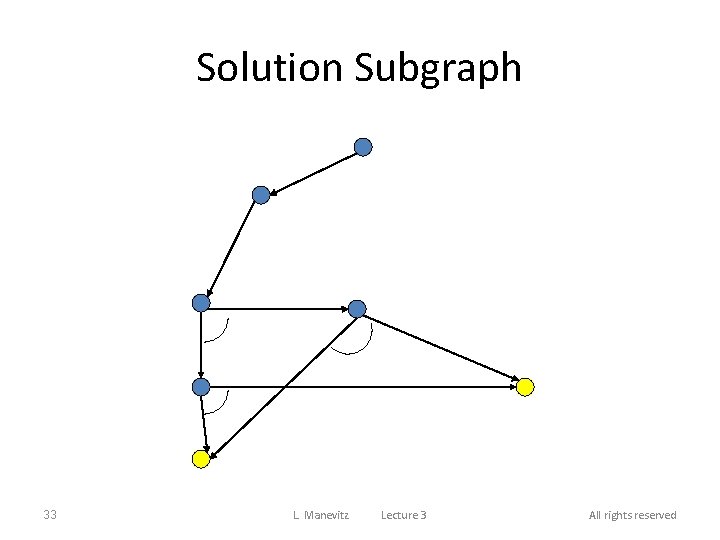
Solution Subgraph 33 L. Manevitz Lecture 3 All rights reserved
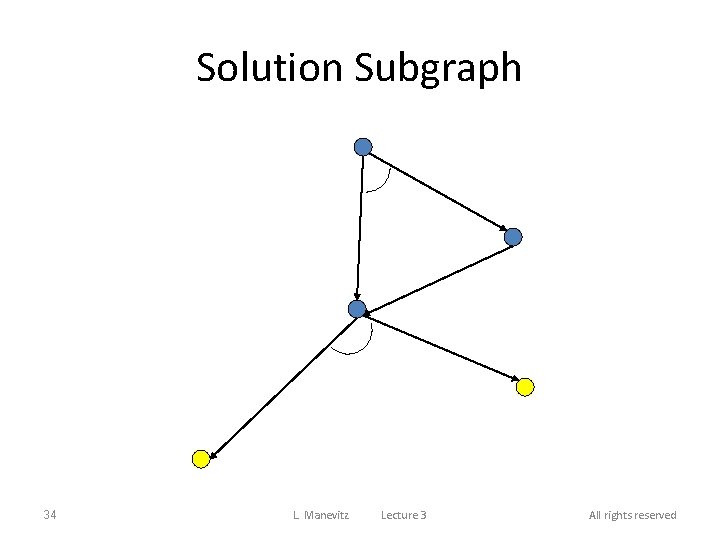
Solution Subgraph 34 L. Manevitz Lecture 3 All rights reserved
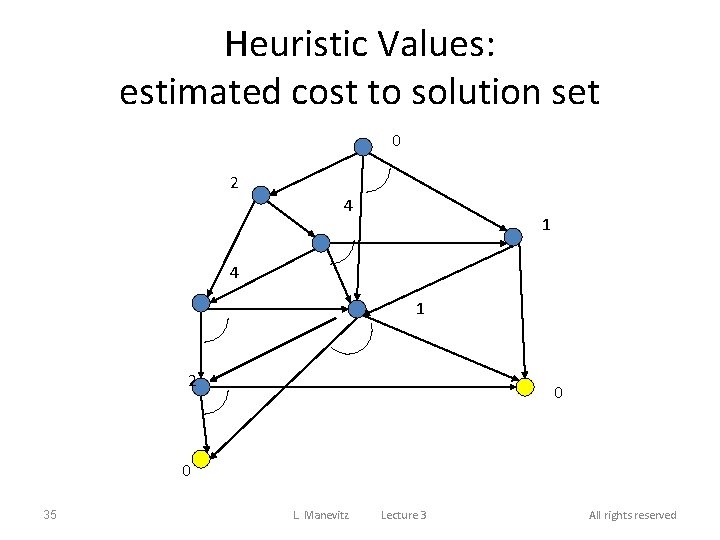
Heuristic Values: estimated cost to solution set 0 2 4 1 2 0 0 35 L. Manevitz Lecture 3 All rights reserved

Basic Idea of A/O* • First top-down graph growing picks out best available partial solution sub-graph from explicit graph. • One leaf node of this graph is expanded • Second, bottom-up cost-revising, connectormarking, SOLVE-labeling. 36 L. Manevitz Lecture 3 All rights reserved

AO* Algorithm 1. Create G = <s> ; q(s) = h (s) If s e TERM mark s SOLVED 2. Until s labeled SOLVED do: 1. Compute G’ partial solution subgraph of G by tracing down marked connectors in G from s. 2. Select n in G’, n not in TERM, n a leaf. 3. Expand n , place successors in G, for each successor not already in G let q(successor)=h (successor). Label SOLVED all successors in TERM. (If no successors, reset q(n) : = infinity ). 37 L. Manevitz Lecture 3 All rights reserved

AO* Algorithm cont. 4. Let S : = {n}. 5. Until S = f do : 1. Remove a node, m, from S which has no descendent in G also in S (minimal node). 2. Revise cost for m, (check each connector from m) q(m)=min [c +q(n 1)+…+q(nk)]. Mark chosen connector. If all successors their connectors are SOLVED then mark m SOLVED. 3. If m SOLVED or changed q(m) then add to S all “preferred” parents of m. 4. End. 6. End. 38 L. Manevitz Lecture 3 All rights reserved

Montone Restriction • h(n) <= c + h(n 1) + h(n 2) + … h(nk) Where c is cost of connector between n and set of n 1, … , nk. This guarantees that h(n) <= h*(n). 39 L. Manevitz Lecture 3 All rights reserved

Cost (q(n) ) Values • If n has no successors then q(n) = h (n) • Otherwise working from bottom, – q(n) = connector cost + sum of q(successors) Pick smallest of above; and mark direction. If that direction has all successors SOLVED then n is marked SOLVED. 40 L. Manevitz Lecture 3 All rights reserved

AO* weighted Example http: //artificialintelligence-notes. blogspot. co. il/2010/07/problem-reduction-with-ao-algorithm. html (Refered From Artificial Intelligence TMH)
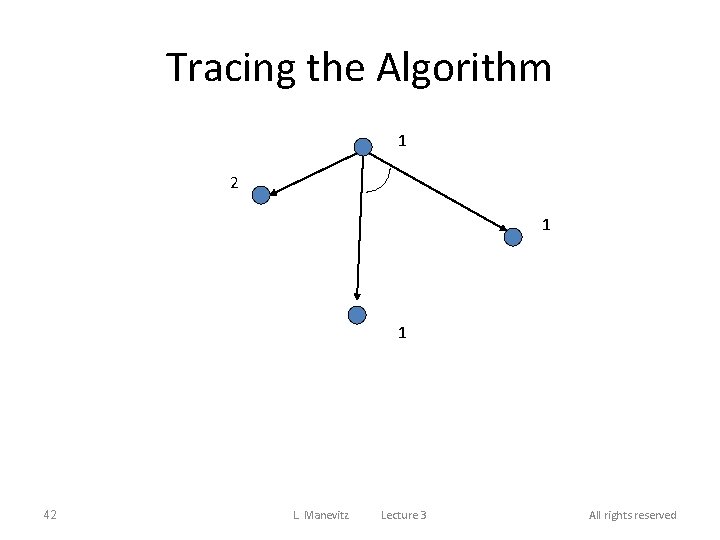
Tracing the Algorithm 1 2 1 1 42 L. Manevitz Lecture 3 All rights reserved
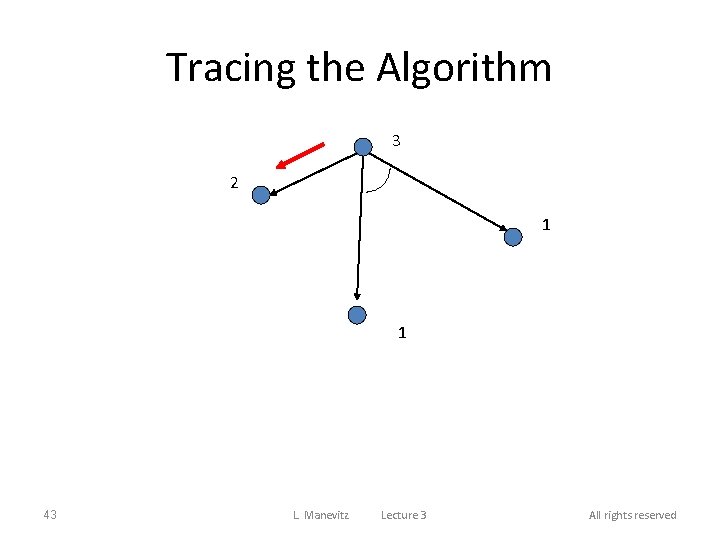
Tracing the Algorithm 3 2 1 1 43 L. Manevitz Lecture 3 All rights reserved
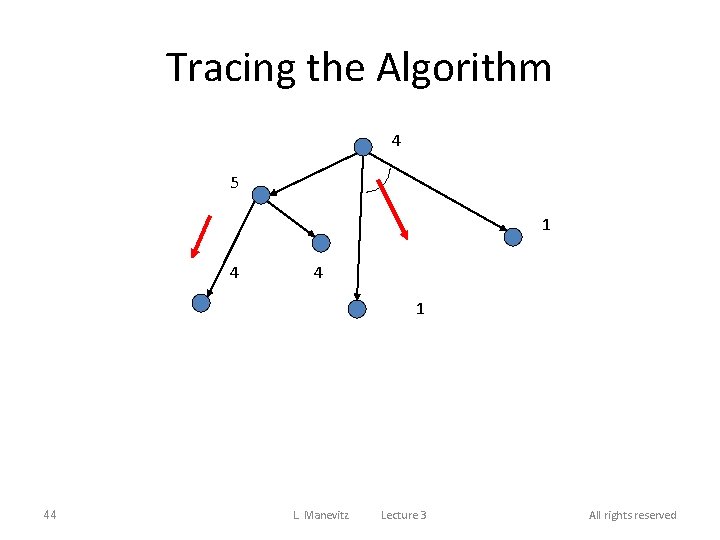
Tracing the Algorithm 4 5 1 4 4 1 44 L. Manevitz Lecture 3 All rights reserved
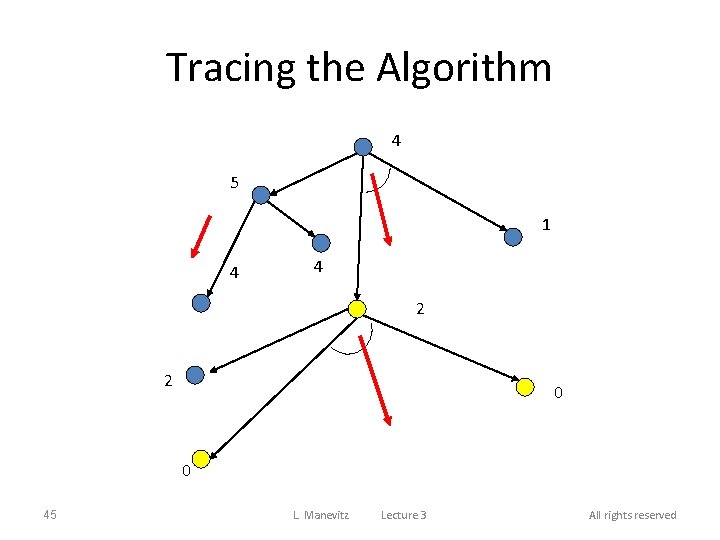
Tracing the Algorithm 4 5 1 4 4 2 2 0 0 45 L. Manevitz Lecture 3 All rights reserved
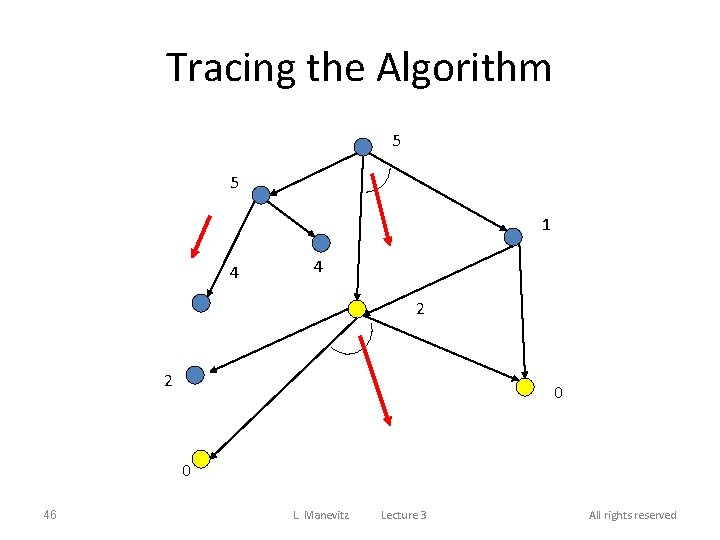
Tracing the Algorithm 5 5 1 4 4 2 2 0 0 46 L. Manevitz Lecture 3 All rights reserved
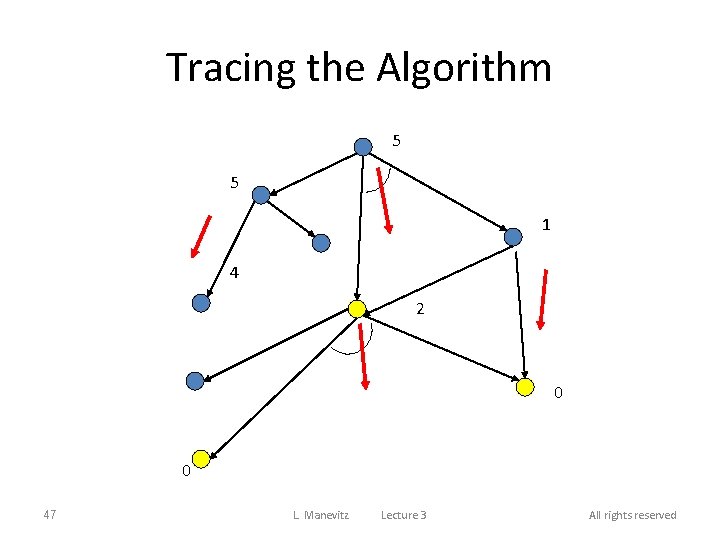
Tracing the Algorithm 5 5 1 4 2 0 0 47 L. Manevitz Lecture 3 All rights reserved
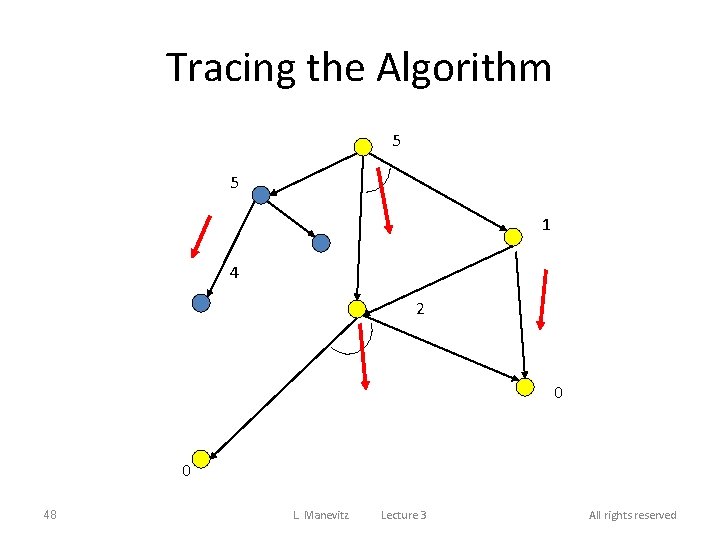
Tracing the Algorithm 5 5 1 4 2 0 0 48 L. Manevitz Lecture 3 All rights reserved

- Slides: 49