DivideandConquer DivideandConquer The most wellknown algorithm design strategy

Divide-and-Conquer

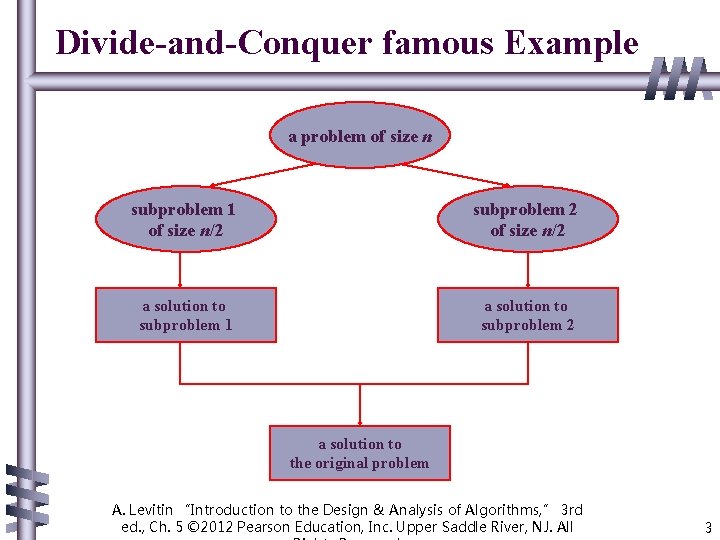
Divide-and-Conquer The most well-known algorithm design strategy: 1. Divide instance of problem into two or more smaller instances 2. Solve smaller instances recursively 3. Obtain solution to original (larger) instance by combining these solutions A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All 2

Divide-and-Conquer famous Example a problem of size n subproblem 1 of size n/2 subproblem 2 of size n/2 a solution to subproblem 1 a solution to subproblem 2 a solution to the original problem A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All 3

General Concept of Divide & Conquer Given a function to compute on n inputs, the divide-andconquer strategy consists of: 1. splitting input into k distinct subsets, 1<k<n, yielding k subproblems. 2. solving these subproblems 3. combining the sub-solutions into solution of the whole problem. • if the subproblems are relatively large, then divide-and-conquer is applied again. • if the subproblems are small, the are solved without splitting. 4

The Divide and Conquer Algorithm Divide_Conquer(problem P){ if Small(P) return Simple. Solution(P); else { divide P into smaller instances P 1, P 2, …, Pk, k 2; Apply Divide_Conquer to each of these subproblems; } return Combine(Divide_Conque(P 1), Divide_Conque(P 2), …, Divide_Conque(Pk)); } 5

Divide and Conquer Three Steps of The Divide and Conquer Approach 1. Divide the problem into two or more smaller subproblems. 2. Conquer the subproblems by solving them recursively. 3. Combine the solutions to the subproblems into the solutions for the original problem. 6

Divide and Conquer Runtime b Master Theorem is optional in our course b An instance of size n can be divided into b instances of size n/b, with a of them needing to be solved. (a and b are constants; a ≥ 1 and b > 1. ) b Runtime is given by 7

Divide-and-Conquer Examples b Sorting: mergesort and quicksort b Counting inversions b Closest-pair algorithm A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All 8

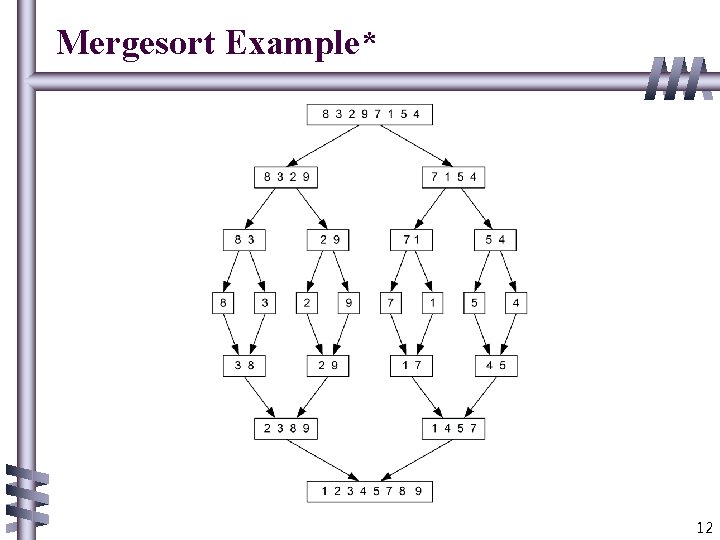
Mergesort b b b Split array A[0. . n-1] in two about equal halves and make copies of each half in arrays B and C Sort arrays B and C recursively Merge sorted arrays B and C into array A as follows: • Repeat the following until no elements remain in one of the arrays: – compare the first elements in the remaining unprocessed portions of the arrays – copy the smaller of the two into A, while incrementing the index indicating the unprocessed portion of that array • Once all elements in one of the arrays are processed, copy the remaining unprocessed elements from the other array into A. 9

Pseudocode of Mergesort 10

Pseudocode of Merge 11

Mergesort Example* 12

Analysis of Mergesort b All cases have same efficiency: Θ(n log n) b Number of comparisons in the worst case is close to theoretical minimum for comparison-based sorting: log 2 n! ≈ n log 2 n - 1. 44 n b Space requirement: Θ(n) (not in-place) b Stable? yes b Can be implemented without recursion (bottom-up) 13

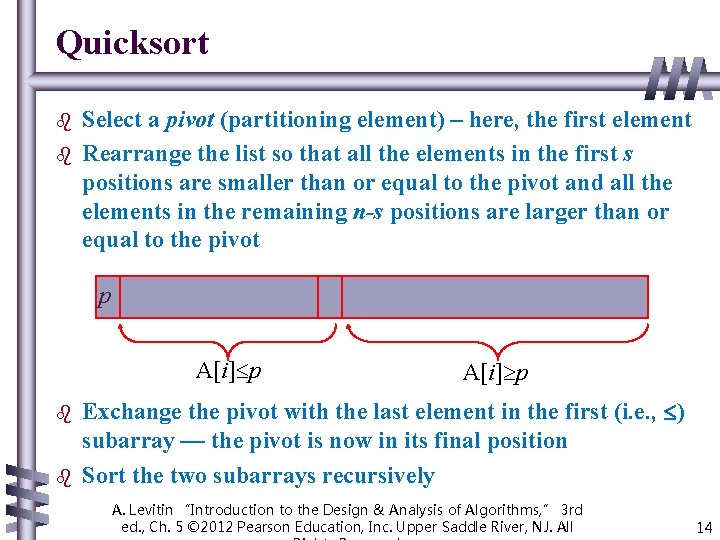
Quicksort b b Select a pivot (partitioning element) – here, the first element Rearrange the list so that all the elements in the first s positions are smaller than or equal to the pivot and all the elements in the remaining n-s positions are larger than or equal to the pivot p A[i] p b b A[i] p Exchange the pivot with the last element in the first (i. e. , ) subarray — the pivot is now in its final position Sort the two subarrays recursively A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All 14

Hoare’s Partitioning Algorithm b 2 directional scan b Full details in [L] page 177 -178 15

Hoare’s Partitioning Algorithm 16

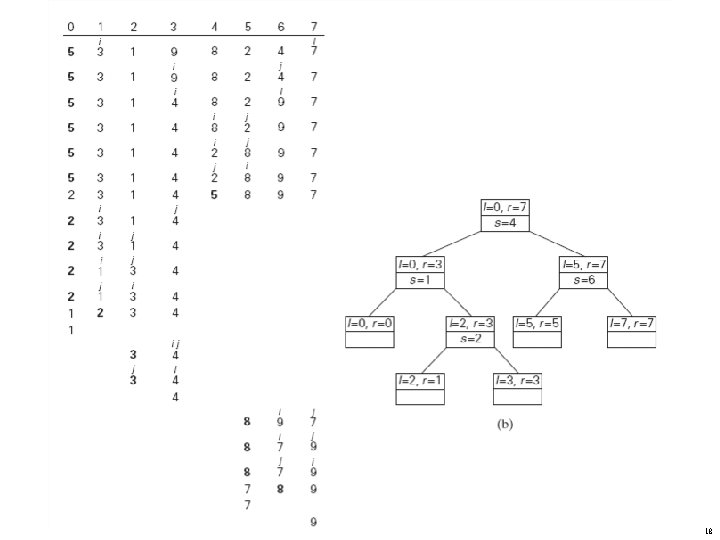
Quicksort Example 5 2 9 1 4 8 3 7 2 3 1 4 5 8 9 7 1 2 3 4 5 7 8 9 A. Levitin “Introduction to the Design & Analysis of Algorithms, ” 3 rd ed. , Ch. 5 © 2012 Pearson Education, Inc. Upper Saddle River, NJ. All 17

Quicksort Example 18

Analysis of Quicksort b b b Best case: split in the middle — Θ(n log n) Worst case: sorted array! — Θ(n 2) Average case: random arrays — Θ(n log n) b Improvements: • better pivot selection: median of three partitioning • switch to insertion sort on small subfiles • elimination of recursion These combine to 20 -25% improvement b Stable ? No 19

[K] 5. 3 Counting Inversions

Counting Inversions Music site tries to match your song preferences with others. You rank n songs. Music site consults database to find people with similar tastes. n n Similarity metric: number of inversions between two rankings. My rank: 1, 2, …, n. Your rank: a 1, a 2, …, an. Songs i and j inverted if i < j, but ai > aj. n n n Songs A B C D E Me 1 2 3 4 5 You 1 3 4 2 5 Inversions 3 -2, 4 -2 Brute force: check all (n 2) pairs i and j. 21

Applications. Voting theory. Collaborative filtering. Measuring the "sortedness" of an array. Sensitivity analysis of Google's ranking function. Rank aggregation for meta-searching on the Web. Nonparametric statistics (e. g. , Kendall's Tau distance). etc. n n n n 22

Counting Inversions: Divide-and-Conquer Divide-and-conquer. 1 5 4 8 10 2 6 9 12 11 3 7 23

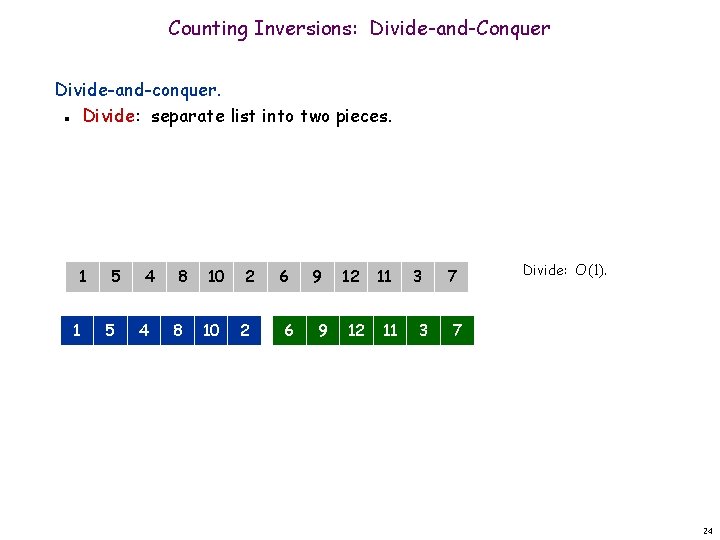
Counting Inversions: Divide-and-Conquer Divide-and-conquer. Divide: separate list into two pieces. n 1 1 5 5 4 4 8 8 10 10 2 2 6 6 9 9 12 12 11 11 3 3 7 Divide: O(1). 7 24

Counting Inversions: Divide-and-Conquer Divide-and-conquer. Divide: separate list into two pieces. Conquer: recursively count inversions in each half. n n 1 1 5 5 4 4 8 8 10 10 5 blue-blue inversions 5 -4, 5 -2, 4 -2, 8 -2, 10 -2 2 2 6 6 9 9 12 12 11 11 3 3 7 7 Divide: O(1). Conquer: 2 T(n / 2) 8 green-green inversions 6 -3, 9 -7, 12 -3, 12 -7, 12 -11, 11 -3, 11 -7 25

Counting Inversions: Divide-and-Conquer Divide-and-conquer. Divide: separate list into two pieces. Conquer: recursively count inversions in each half. Combine: count inversions where ai and aj are in different halves, and return sum of three quantities. n n n 1 1 5 5 4 4 8 8 10 10 2 2 6 6 5 blue-blue inversions 9 9 12 12 11 11 3 3 7 7 Divide: O(1). Conquer: 2 T(n / 2) 8 green-green inversions 9 blue-green inversions 5 -3, 4 -3, 8 -6, 8 -3, 8 -7, 10 -6, 10 -9, 10 -3, 10 -7 Combine: ? ? ? Total = 5 + 8 + 9 = 22. 26

Counting Inversions: Combine: count blue-green inversions Assume each half is sorted. Count inversions where ai and aj are in different halves. Merge two sorted halves into sorted whole. n n n to maintain sorted invariant 3 7 10 14 18 19 2 11 16 17 23 25 6 3 2 2 0 0 13 blue-green inversions: 6 + 3 + 2 + 0 2 3 7 10 11 14 16 17 18 19 Count: O(n) 23 25 Merge: O(n) 27

Counting Inversions: Implementation Pre-condition. [Merge-and-Count] A and B are sorted. Post-condition. [Sort-and-Count] L is sorted. Sort-and-Count(L) { if list L has one element return 0 and the list L Divide the list into two halves A and B (r. A, A) Sort-and-Count(A) (r. B, B) Sort-and-Count(B) (r. B, L) Merge-and-Count(A, B) } return r = r. A + r. B + r and the sorted list L 28

Counting Inversions: Implementation Merge-and-Count(A, B) Maintain a Current pointer into each list, initialized to point to the front elements Inversions_count = 0 While both lists are not empty: Let ai and bj be the elements pointed to by the pointers Append the smaller of these two to the output list If bj is the smaller element then Inversions_count += the number of elements remaining in A Endif Advance the Current pointer in the list from which the smaller element was selected. End. While Once one list is empty, append the remainder of the other list to the output Return Inversions_count and the merged list 29

Closest Pair of Points

Closest Pair of Points Closest pair. Given n points in the plane, find a pair with smallest Euclidean distance between them. Fundamental geometric primitive. Graphics, computer vision, geographic information systems, molecular modeling, air traffic control. Special case of nearest neighbor. n n fast closest pair inspired fast algorithms for these problems Brute force. Check all pairs of points p and q with (n 2) comparisons. 1 -D version. O(n log n) easy if points are on a line. *How? Assumption. No two points have same x coordinate. Only to make presentation cleaner 31

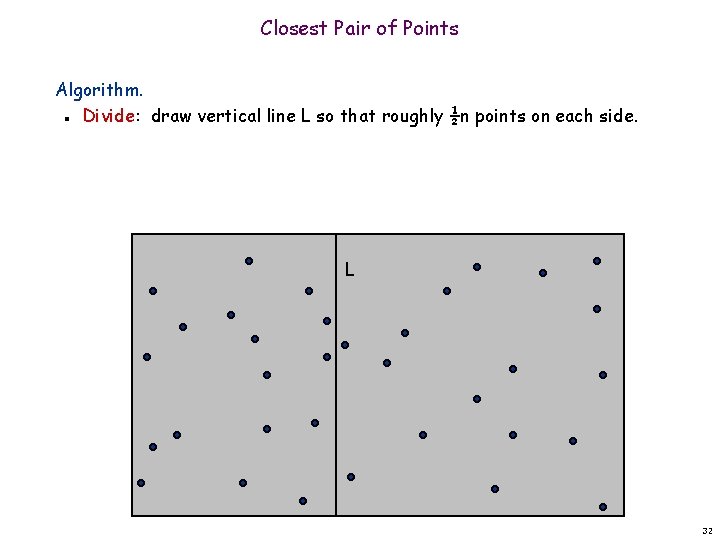
Closest Pair of Points Algorithm. Divide: draw vertical line L so that roughly ½n points on each side. n L 32

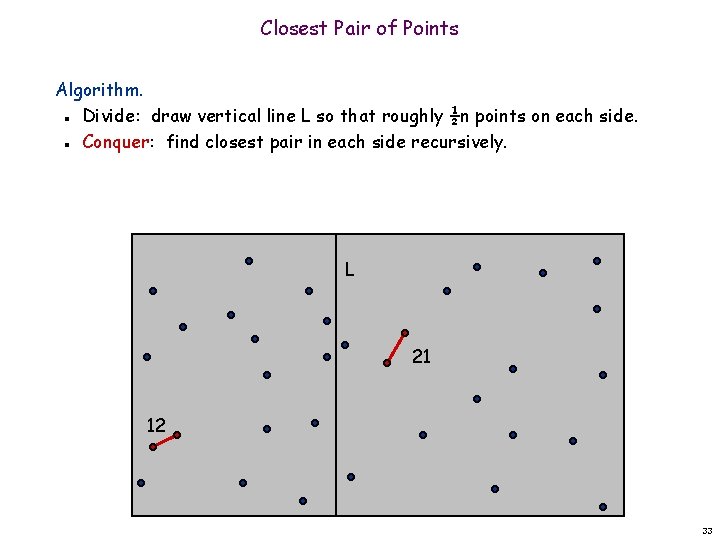
Closest Pair of Points Algorithm. Divide: draw vertical line L so that roughly ½n points on each side. Conquer: find closest pair in each side recursively. n n L 21 12 33

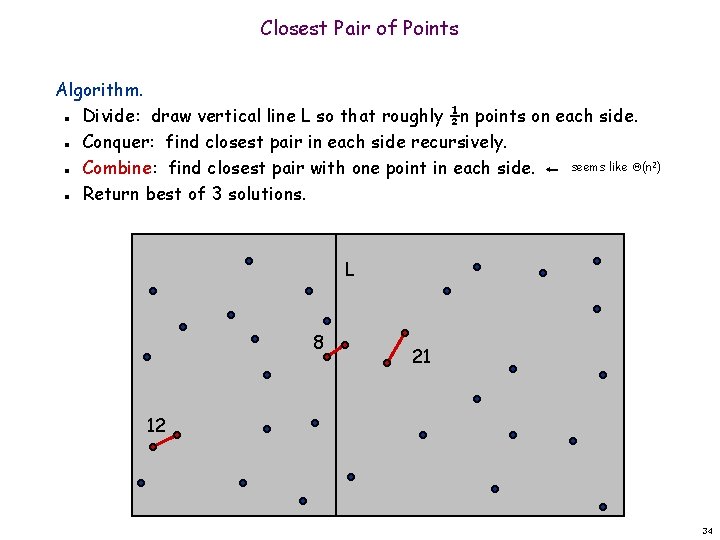
Closest Pair of Points Algorithm. Divide: draw vertical line L so that roughly ½n points on each side. Conquer: find closest pair in each side recursively. seems like (n 2) Combine: find closest pair with one point in each side. Return best of 3 solutions. n n L 8 21 12 34

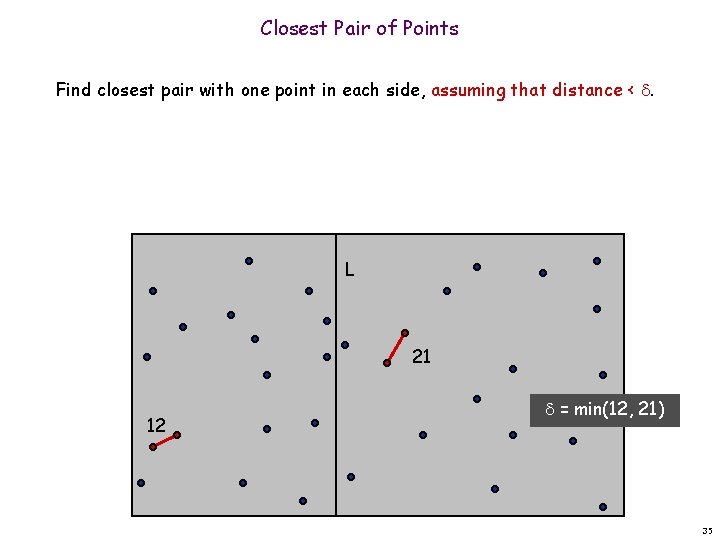
Closest Pair of Points Find closest pair with one point in each side, assuming that distance < . L 21 12 = min(12, 21) 35

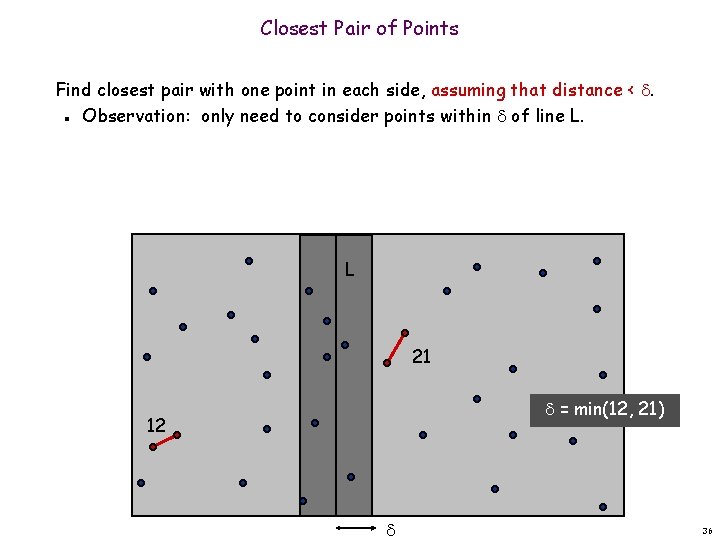
Closest Pair of Points Find closest pair with one point in each side, assuming that distance < . Observation: only need to consider points within of line L. n L 21 = min(12, 21) 12 36

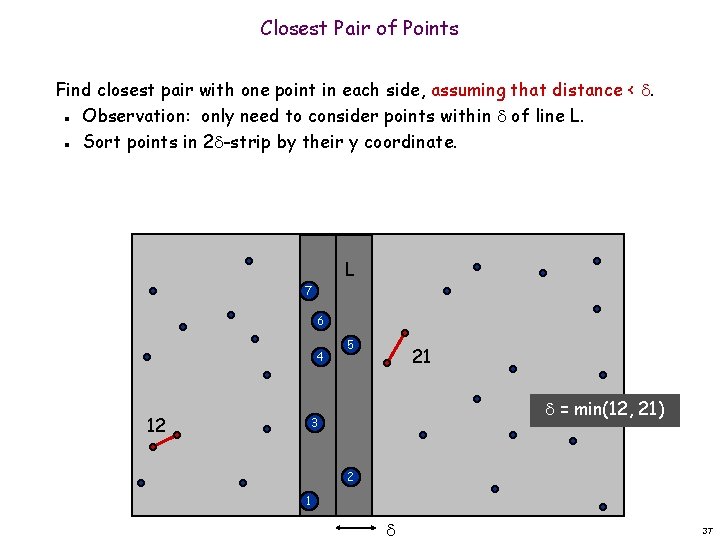
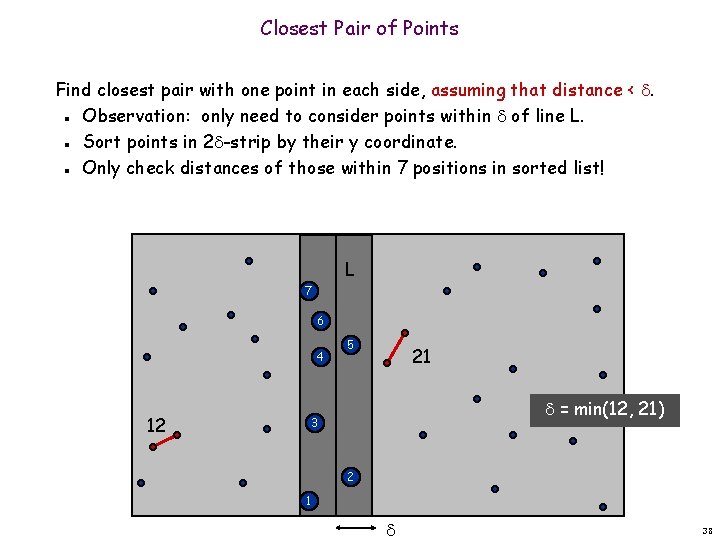
Closest Pair of Points Find closest pair with one point in each side, assuming that distance < . Observation: only need to consider points within of line L. Sort points in 2 -strip by their y coordinate. n n L 7 6 4 12 5 21 = min(12, 21) 3 2 1 37

Closest Pair of Points Find closest pair with one point in each side, assuming that distance < . Observation: only need to consider points within of line L. Sort points in 2 -strip by their y coordinate. Only check distances of those within 7 positions in sorted list! n n n L 7 6 4 12 5 21 = min(12, 21) 3 2 1 38

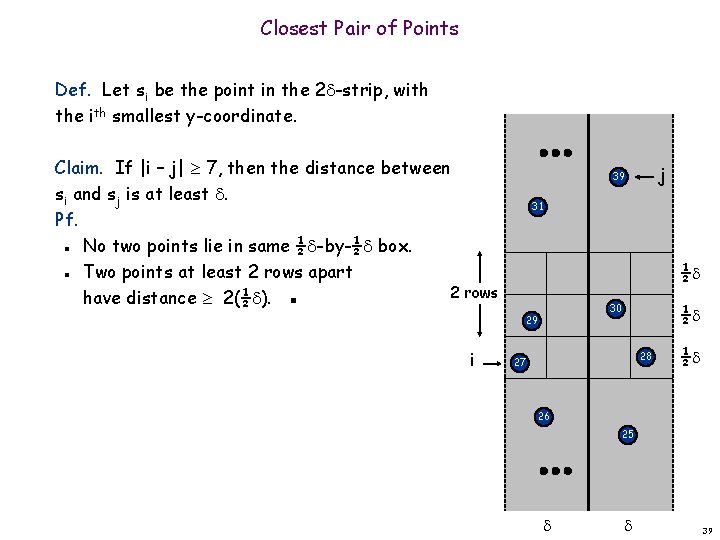
Closest Pair of Points Def. Let si be the point in the 2 -strip, with the ith smallest y-coordinate. Claim. If |i – j| 7, then the distance between si and sj is at least . Pf. No two points lie in same ½ -by-½ box. Two points at least 2 rows apart 2 rows have distance 2(½ ). ▪ j 39 31 n ½ n i ½ 30 29 28 27 ½ 26 25 39

O(n log n) 40

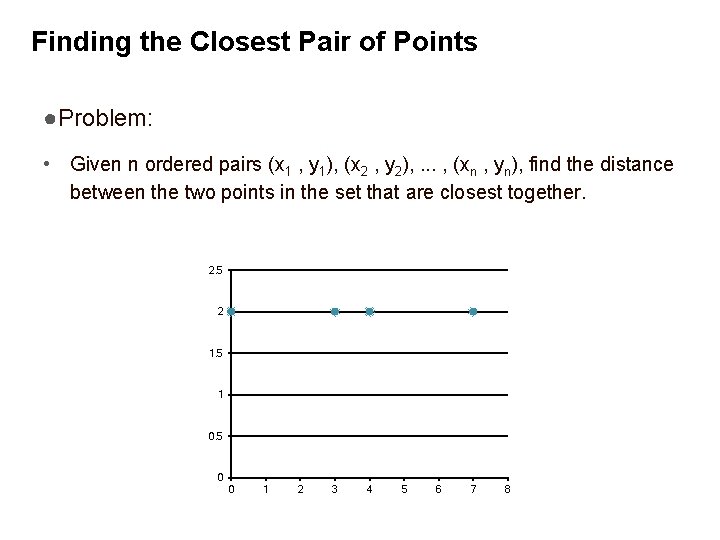
Finding the Closest Pair of Points ●Problem: • Given n ordered pairs (x 1 , y 1), (x 2 , y 2), . . . , (xn , yn), find the distance between the two points in the set that are closest together. 2. 5 2 1. 5 1 0. 5 0 0 1 2 3 4 5 6 7 8

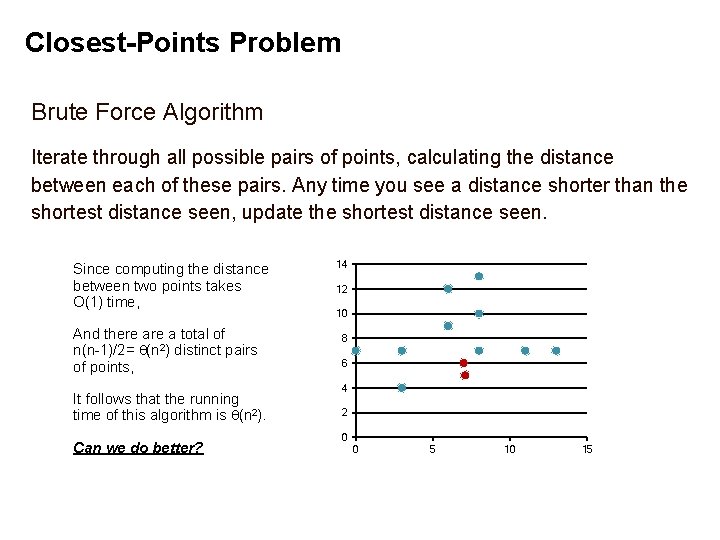
Closest-Points Problem Brute Force Algorithm Iterate through all possible pairs of points, calculating the distance between each of these pairs. Any time you see a distance shorter than the shortest distance seen, update the shortest distance seen. Since computing the distance between two points takes O(1) time, And there a total of n(n-1)/2= (n 2) distinct pairs of points, It follows that the running time of this algorithm is (n 2). Can we do better? 14 12 10 8 6 4 2 0 0 5 10 15

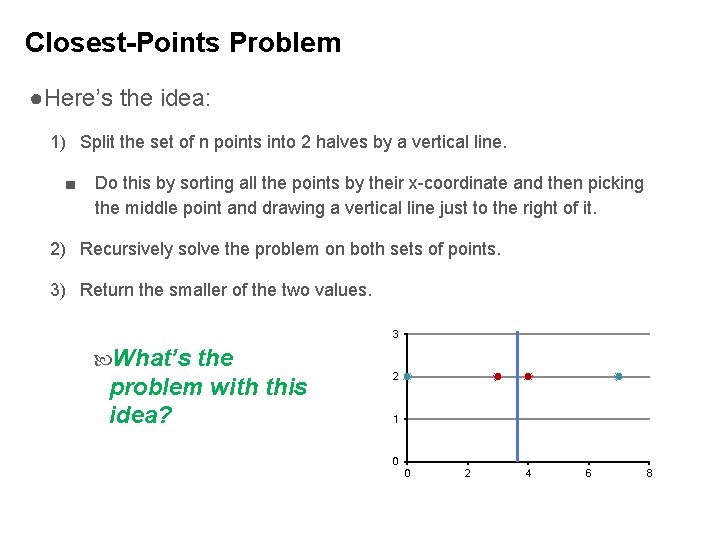
Closest-Points Problem ●Here’s the idea: 1) Split the set of n points into 2 halves by a vertical line. ■ Do this by sorting all the points by their x-coordinate and then picking the middle point and drawing a vertical line just to the right of it. 2) Recursively solve the problem on both sets of points. 3) Return the smaller of the two values. 3 What’s the problem with this idea? 2 1 0 0 2 4 6 8

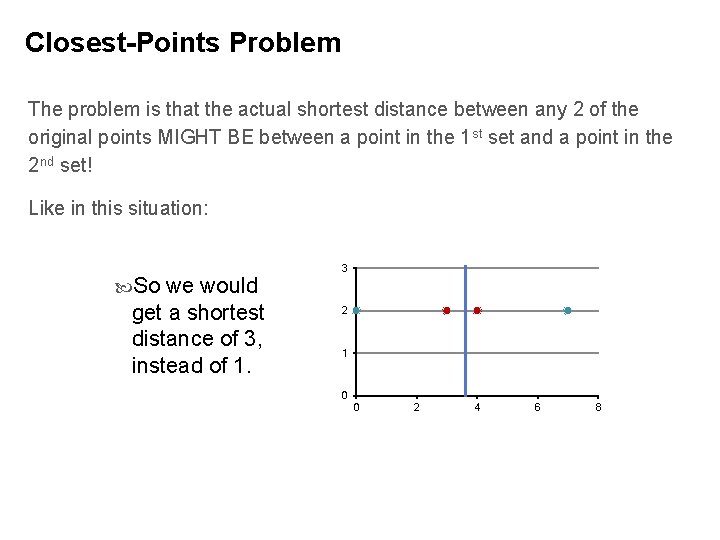
Closest-Points Problem The problem is that the actual shortest distance between any 2 of the original points MIGHT BE between a point in the 1 st set and a point in the 2 nd set! Like in this situation: So we would get a shortest distance of 3, instead of 1. 3 2 1 0 0 2 4 6 8

We must adapt our approach: In step 3, we can “save” the smaller of the two values (called δ), then we have to check to see if there are points that are closer than δ apart. Do we need to search thru all possible pairs of points from the 2 different sides? NO, we can only consider points that are within δ of our dividing line. δ 3 2 1 0 0 2 4 6 8

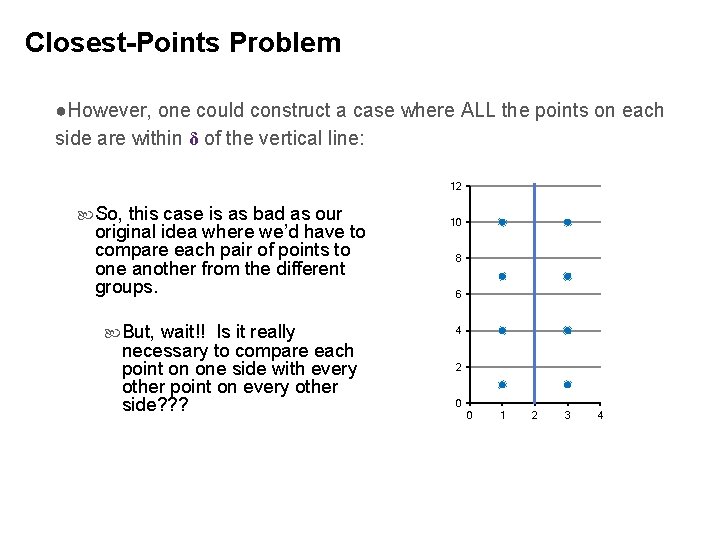
Closest-Points Problem ●However, one could construct a case where ALL the points on each side are within δ of the vertical line: 12 So, this case is as bad as our original idea where we’d have to compare each pair of points to one another from the different groups. But, wait!! Is it really necessary to compare each point on one side with every other point on every other side? ? ? 10 8 6 4 2 0 0 1 2 3 4

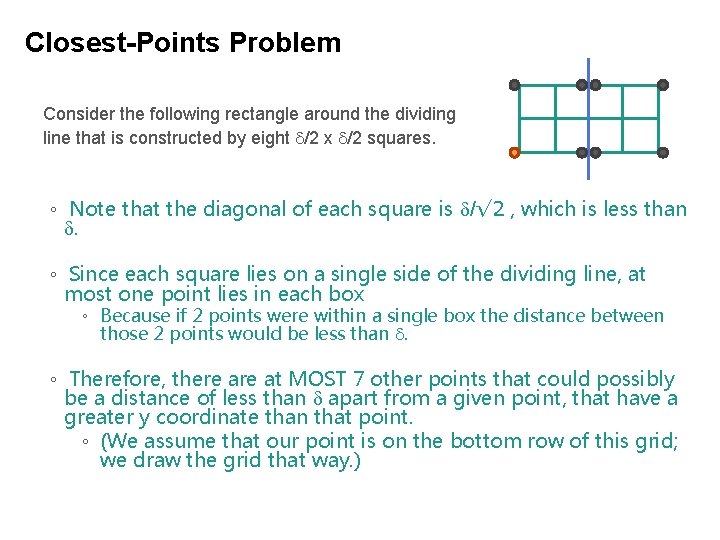
Closest-Points Problem Consider the following rectangle around the dividing line that is constructed by eight /2 x /2 squares. ◦ Note that the diagonal of each square is /√ 2 , which is less than . ◦ Since each square lies on a single side of the dividing line, at most one point lies in each box ◦ Because if 2 points were within a single box the distance between those 2 points would be less than . ◦ Therefore, there at MOST 7 other points that could possibly be a distance of less than apart from a given point, that have a greater y coordinate than that point. ◦ (We assume that our point is on the bottom row of this grid; we draw the grid that way. )

Closest-Points Problem Now we have the issue of how do we know which 7 points to compare a given point with? The idea is: As you are processing the points recursively, SORT them based on the y-coordinate. Then for a given point within the strip, you only need to compare with the next 7 points.

// Combine mid. Point pts. By. X[mid] lr. Dist min(dist. L, dist. R) { Closest. Pair(pts. By. X, pts. By. Y, n) if (n = 1) return 1 if (n = 2) return distance(pts. By. X[0], pts. By. X[1]) Construct array y. Strip, in increasing y order, of all points p in pts. By. Y s. t. |p. x − mid. Point. x| < lr. Dist // Divide into two subproblems mid n/2 -1 copy pts. By. X[0. . . mid] into new array XL in x // Check y. Strip min. Dist lr. Dist for (j 0; j ≤ y. Strip. length − 2; j++) { k j+1 while (k y. Strip. length − 1 and y. Strip[k]. y − y. Strip[j]. y < lr. Dist) { d distance(y. Strip[j], y. Strip[k]) min. Dist min(min. Dist, d) k++ } } return min. Dist order. copy pts. By. X[mid+1. . . n − 1] into new array XR copy pts. By. Y into arrays Y L and Y R in y order, s. t. XL and Y L refer to same points, as do XR, Y R. // Conquer dist. L Closest. Pair(XL, Y L, n/2) dist. R Closest. Pair(XR, Y R, n/2) }

Reading • [L] Chapter 5 • • Section 5. 4 is NOT required All about Convex-Hull is optional [K] Section 5. 3 • • • Section 5. 3 is NOT required All about Trees is not required <yet> All about Graphs is not required <yet> Repeated topics in: • [K] 5. 4 and [C] Chapter 7 50