An Overview of Constraint Programming MSORM 2000 Tutorial

An Overview of Constraint Programming MSORM 2000 Tutorial November 20/21, 2000 Martin Henz, National University of Singapore MSORM 2000 Constraint Programming Tutorial

Material and Other References h Tutorial Material h Slides (distributed in conference bag) h Henz, Müller: An Overview of Finite Domain Constraint Programming (distributed in conference bag) h Programs and slides available at www. comp. nus. edu. sg/~henz/talks/msorm/ h Oz and Mozart h Programming language Oz hdeveloped 1992 -1999 by Programming Systems Lab h Programming system Mozart hdeveloped 1996 -2000 by Mozart Consortium h more information at www. mozart-oz. org MSORM 2000 Constraint Programming Tutorial 2

Initial Remarks h Here, we focus on Finite Domain Constraint Programming CP(FD); CP initially conceived as framework CLP(X) [Jaffar, Lassez 1987] h Communication problems CS OR; Program [Lustig, Puget 1999] h Within CP(FD), we focus on constraint-based tree search h Programming language software framework MSORM 2000 Constraint Programming Tutorial 3

Overview h Constraint I II Programming in a Nutshell h Elements of Constraint Programming h Case study: ACC 97/98 Basketball h Excursions: Constraint Programming in Oz h Constraint Programming Techniques h Constraint-based Scheduling MSORM 2000 Constraint Programming Tutorial 4

Overview h Constraint Programming in a Nutshell h Elements of Constraint Programming h Case study: ACC 97/98 Basketball h Excursions: Constraint Programming in Oz h Constraint Programming Techniques h Constraint-based Scheduling MSORM 2000 Constraint Programming Tutorial 5

Constraint Programming in a Nutshell SEND MSORM 2000 MORE MONEY Constraint Programming Tutorial 6

Constraint Programming in a Nutshell SEND + MORE MSORM 2000 = MONEY Constraint Programming Tutorial 7

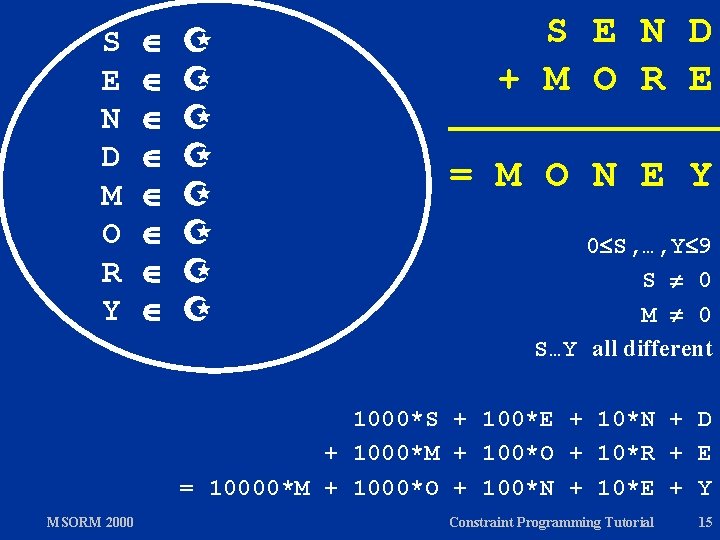
SEND + MORE = MONEY Assign distinct digits to the letters S, E, N, D, M, O, R, Y such that S E N D + M O R E = M O N E Y holds. MSORM 2000 Constraint Programming Tutorial 8

SEND + MORE = MONEY Assign distinct digits to the letters S, E, N, D, M, O, R, Y Solution such that 9 5 6 7 S E N D + 1 0 8 5 + M O R E = M O N E Y = 1 0 6 5 2 holds. MSORM 2000 Constraint Programming Tutorial 9

Modeling Formalize the problem as a constraint problem: h number of variables: n h constraints: c 1, …, cm n h problem: Find a = (v 1, …, vn) n such that a ci , for all 1 i m MSORM 2000 Constraint Programming Tutorial 10

A Model for MONEY h number of variables: 8 h constraints: c 1 = {(S, E, N, D, M, O, R, Y) c 2 = {(S, E, N, D, M, O, R, Y) 1000*S + 1000*M = 10000*M + 1000*O MSORM 2000 8 8 + + + | 0 | 100*E 100*O 100*N S, …, Y 9 } + 10*N + D + 10*R + E + 10*E + Y} Constraint Programming Tutorial 11

A Model for MONEY (continued) h more constraints c 3 = {(S, E, N, D, M, O, R, Y) 8 | S 0 } c 4 = {(S, E, N, D, M, O, R, Y) 8 | M 0 } c 5 = {(S, E, N, D, M, O, R, Y) 8 | S…Y all different} MSORM 2000 Constraint Programming Tutorial 12

Solution for MONEY c 1 = {(S, E, N, D, M, O, R, Y) 8 | 0 S, …, Y 9 } c 2 = {(S, E, N, D, M, O, R, Y) 8 | 1000*S + 100*E + 10*N + D + 1000*M + 100*O + 10*R + E = 10000*M + 1000*O + 100*N + 10*E + Y} c 3 = {(S, E, N, D, M, O, R, Y) 8 | S 0 } c 4 = {(S, E, N, D, M, O, R, Y) 8 | M 0 } c 5 = {(S, E, N, D, M, O, R, Y) 8 | S…Y all different} Solution: (9, 5, 6, 7, 1, 0, 8, 2) 8 MSORM 2000 Constraint Programming Tutorial 13

Elements of Constraint Programming Exploiting constraints during tree search h Use propagation algorithms for constraints h Employ branching algorithm h Execute exploration algorithm MSORM 2000 Constraint Programming Tutorial 14

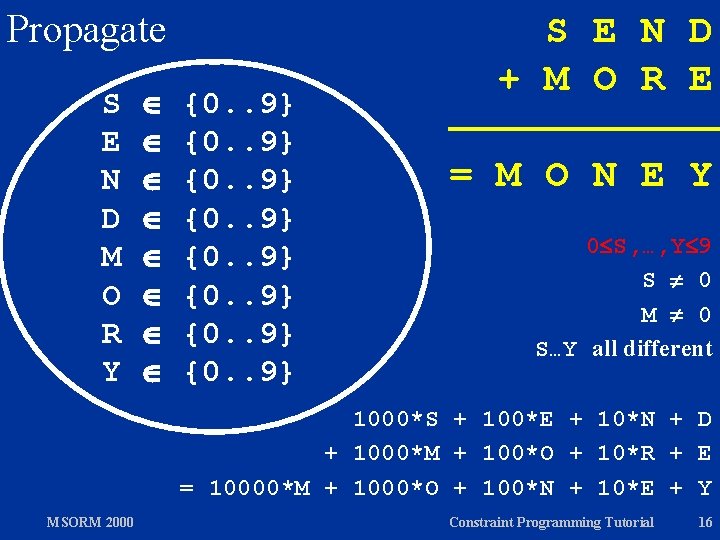
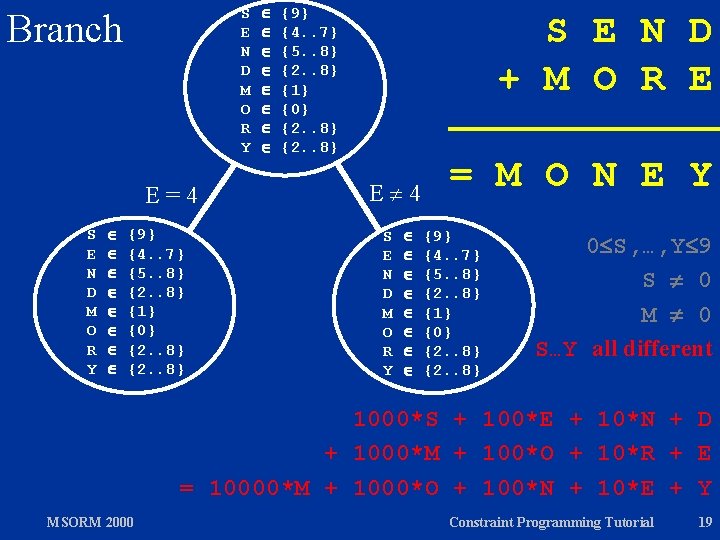
S E N D M O R Y S E N D + M O R E = M O N E Y 0 S, …, Y 9 S 0 M 0 S…Y all different 1000*S + 100*E + 10*N + D + 1000*M + 100*O + 10*R + E = 10000*M + 1000*O + 100*N + 10*E + Y MSORM 2000 Constraint Programming Tutorial 15

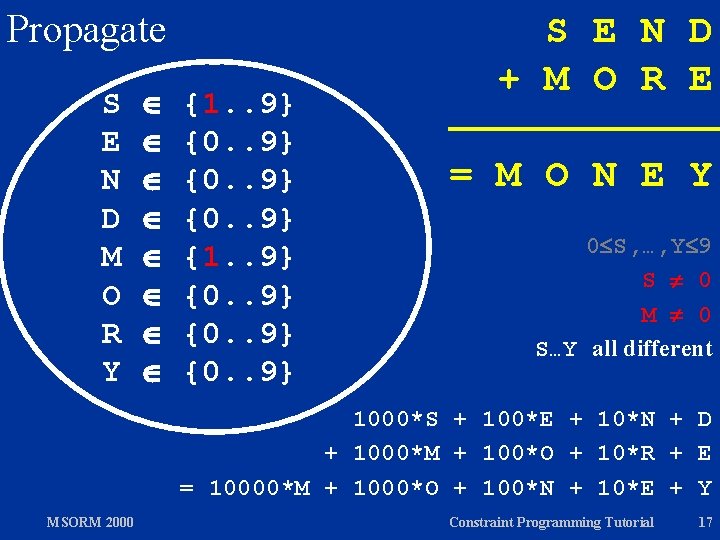
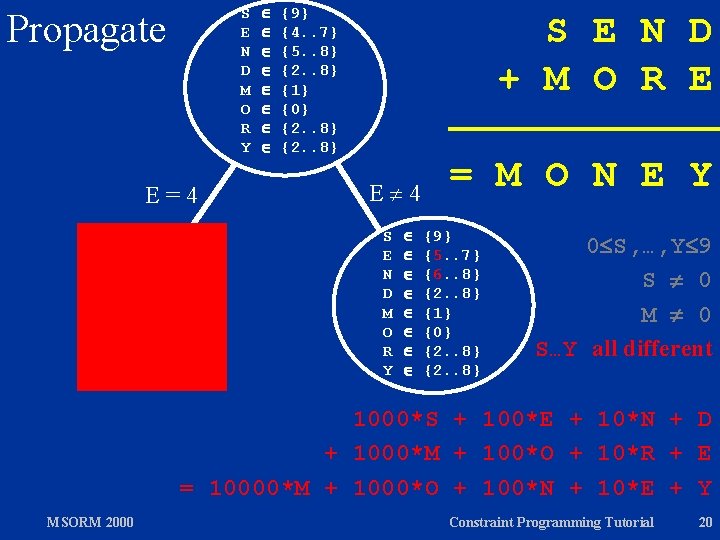
Propagate S E N D M O R Y {0. . 9} {0. . 9} S E N D + M O R E = M O N E Y 0 S, …, Y 9 S 0 M 0 S…Y all different 1000*S + 100*E + 10*N + D + 1000*M + 100*O + 10*R + E = 10000*M + 1000*O + 100*N + 10*E + Y MSORM 2000 Constraint Programming Tutorial 16

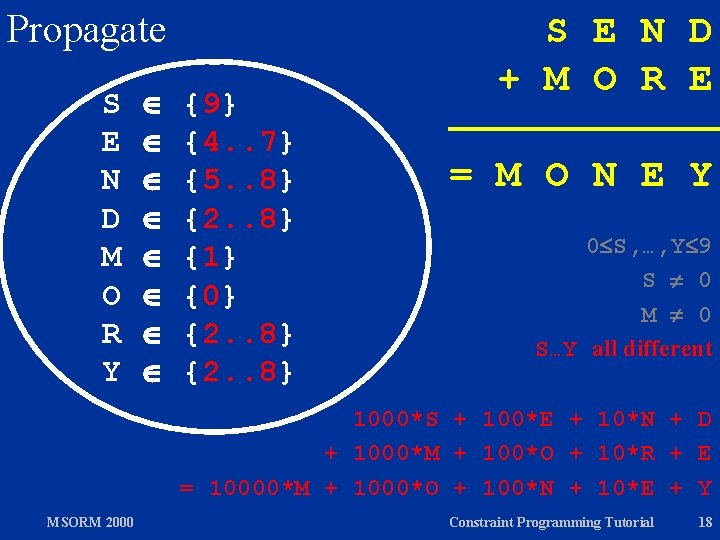
Propagate S E N D M O R Y {1. . 9} {0. . 9} S E N D + M O R E = M O N E Y 0 S, …, Y 9 S 0 M 0 S…Y all different 1000*S + 100*E + 10*N + D + 1000*M + 100*O + 10*R + E = 10000*M + 1000*O + 100*N + 10*E + Y MSORM 2000 Constraint Programming Tutorial 17

Propagate S E N D M O R Y {9} {4. . 7} {5. . 8} {2. . 8} {1} {0} {2. . 8} S E N D + M O R E = M O N E Y 0 S, …, Y 9 S 0 M 0 S…Y all different 1000*S + 100*E + 10*N + D + 1000*M + 100*O + 10*R + E = 10000*M + 1000*O + 100*N + 10*E + Y MSORM 2000 Constraint Programming Tutorial 18

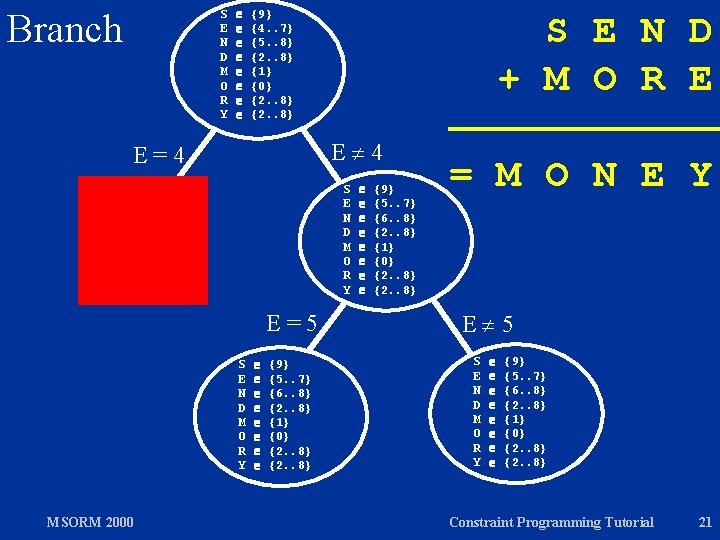
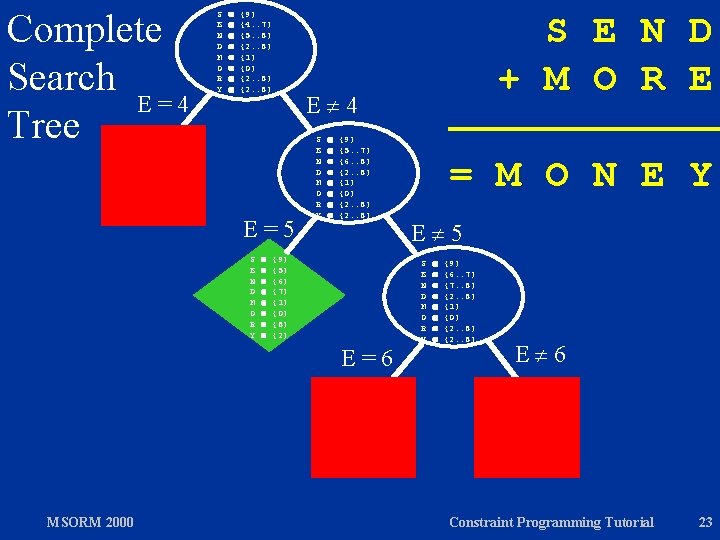
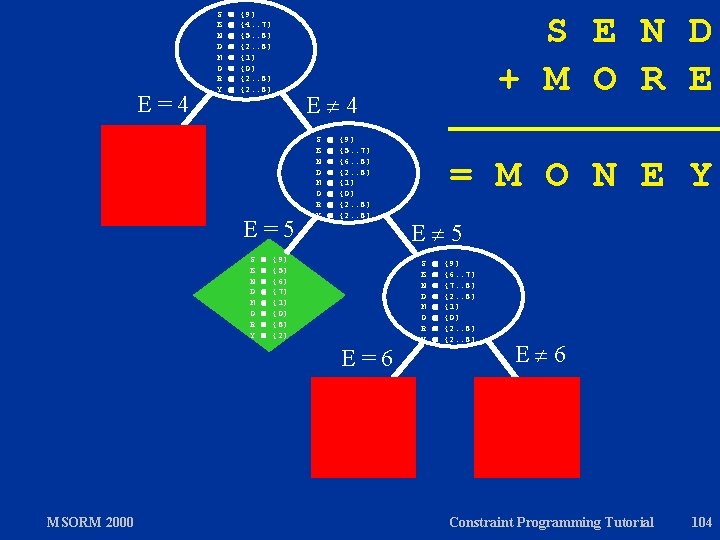
S E N D M O R Y Branch E=4 S E N D M O R Y {9} {4. . 7} {5. . 8} {2. . 8} {1} {0} {2. . 8} S E N D + M O R E E 4 S E N D M O R Y = M O N E Y {9} {4. . 7} {5. . 8} {2. . 8} {1} {0} {2. . 8} 0 S, …, Y 9 S 0 M 0 S…Y all different 1000*S + 100*E + 10*N + D + 1000*M + 100*O + 10*R + E = 10000*M + 1000*O + 100*N + 10*E + Y MSORM 2000 Constraint Programming Tutorial 19

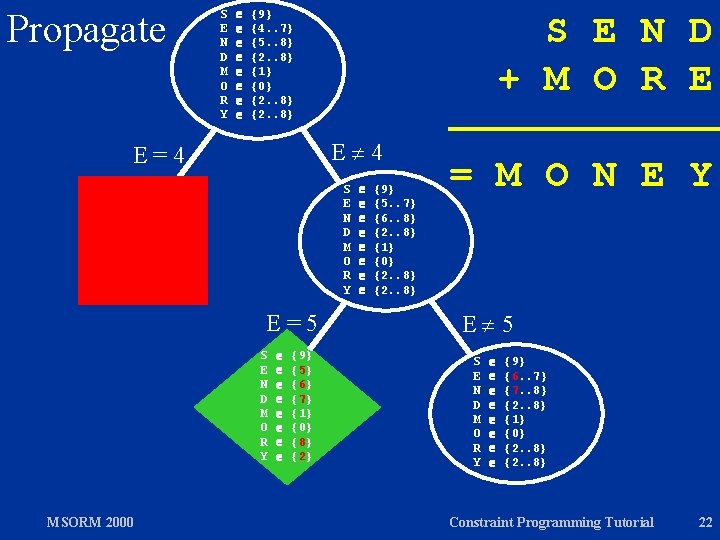
S E N D M O R Y Propagate E=4 {9} {4. . 7} {5. . 8} {2. . 8} {1} {0} {2. . 8} S E N D + M O R E E 4 S E N D M O R Y = M O N E Y {9} {5. . 7} {6. . 8} {2. . 8} {1} {0} {2. . 8} 0 S, …, Y 9 S 0 M 0 S…Y all different 1000*S + 100*E + 10*N + D + 1000*M + 100*O + 10*R + E = 10000*M + 1000*O + 100*N + 10*E + Y MSORM 2000 Constraint Programming Tutorial 20

Branch S E N D M O R Y {9} {4. . 7} {5. . 8} {2. . 8} {1} {0} {2. . 8} S E N D + M O R E E 4 E=4 S E N D M O R Y E=5 S E N D M O R Y MSORM 2000 {9} {5. . 7} {6. . 8} {2. . 8} {1} {0} {2. . 8} = M O N E Y E 5 S E N D M O R Y {9} {5. . 7} {6. . 8} {2. . 8} {1} {0} {2. . 8} Constraint Programming Tutorial 21

Propagate S E N D M O R Y {9} {4. . 7} {5. . 8} {2. . 8} {1} {0} {2. . 8} S E N D + M O R E E 4 E=4 S E N D M O R Y E=5 S E N D M O R Y MSORM 2000 {9} {5} {6} {7} {1} {0} {8} {2} {9} {5. . 7} {6. . 8} {2. . 8} {1} {0} {2. . 8} = M O N E Y E 5 S E N D M O R Y {9} {6. . 7} {7. . 8} {2. . 8} {1} {0} {2. . 8} Constraint Programming Tutorial 22

Complete Search E=4 Tree S E N D M O R Y {9} {4. . 7} {5. . 8} {2. . 8} {1} {0} {2. . 8} E 4 E=5 S E N D M O R Y {9} {5. . 7} {6. . 8} {2. . 8} {1} {0} {2. . 8} {9} {5} {6} {7} {1} {0} {8} {2} E=6 MSORM 2000 S E N D + M O R E = M O N E Y E 5 S E N D M O R Y {9} {6. . 7} {7. . 8} {2. . 8} {1} {0} {2. . 8} E 6 Constraint Programming Tutorial 23

Relation to Integer Programming h More general notion of problem; constraints can be any relation, not just arithmetic or even just linear arithmetic constraints h De-emphasize optimization (optimization as after-thought) h Focus on software engineering h no push-button solver, but glass-box or no-box h experimentation platforms h extensive support for “performance debugging” MSORM 2000 Constraint Programming Tutorial 24

Constraint Programming Systems Role: support elements of constraint programming h Provide propagation algorithms for constraints h all different (e. g. wait for fixing) h summation (e. g. interval consistency) h Allow choice of branching algorithm (e. g. first-fail) h Allow choice of exploration algorithm (e. g. depth-first search) MSORM 2000 Constraint Programming Tutorial 25

Using Oz proc {Money Root} S E N D M O R Y in Root=sol(s: S e: E n: N d: D m: M o: O r: R Root : : : 0#9 {FD. distinct Root} S =: 0 M =: 0 1000*S + 100*E + 10*N + + 1000*M + 100*O + 10*R + =: 10000*M + 1000*O + 100*N + 10*E + {FD. distribute ff Root} end {Explore. All Money} y: Y) Modeling D E Y Propagation Branching Exploration MONEY Demo MSORM 2000 Constraint Programming Tutorial 26

The Art of Constraint Programming h Choose model h Choose propagation algorithms h Choose branching algorithm h Choose exploration algorithm MSORM 2000 Constraint Programming Tutorial 27

Programming Systems for Finite Domain Constraint Programming h Finite domain constraint programming libraries h PECOS [Puget 1992] h ILOG Solver [Puget 1993] h Finite domain constraint programming languages h CHIP [Dincbas, Hentenryck, Simonis, Aggoun 1988] h SICStus Prolog [Haridi, Carlson 1995] h Oz [Smolka and others 1995] h CLAIRE [Caseau, Laburthe 1996] h OPL [van Hentenryck 1998] MSORM 2000 Constraint Programming Tutorial 28

Overview h Constraint Programming in a Nutshell h Elements of Constraint Programming h Case study: ACC 97/98 Basketball h Excursions: Constraint Programming in Oz h Constraint Programming Techniques h Constraint-based Scheduling MSORM 2000 Constraint Programming Tutorial 29

Constraint Problems A finite domain constraint problem consists of: h number of variables: n h constraints: c 1, …, cm n The problem is to find a = (v 1, …, vn) n such that a ci , for all 1 i m MSORM 2000 Constraint Programming Tutorial 30

Constraint Solving Given: a satisfiable constraint C and a new constraint C’. Constraint solving means deciding whether C C’ is satisfiable. Example: C: C’: MSORM 2000 n > 2 an + bn = cn Constraint Programming Tutorial 31

Constraint Solving Constraint solving is not possible for general constraints. Constraint programming separates constraints into h basic constraints: complete constraint solving h non-basic constraints: propagation (incomplete); search needed MSORM 2000 Constraint Programming Tutorial 32

Basic Constraints in Finite Domain Constraint Programming h Basic constraints are conjunctions of constraints of the form X S, where S is a finite set of integers. h Constraint solving is done by intersecting domains. Example: C= ( X {1. . 10} Y {9. . 20} ) C’ = ( X {9. . 15} Y {14. . 30} ) h In practice, we keep a solved form, storing the current domain of every variable. MSORM 2000 Constraint Programming Tutorial 33

Basic Constraints and Propagators 1000*S + 100*E + 10*N + D + 1000*M + 100*O + 10*R + E = 10000*M + 1000*O + 100*N + 10*E + Y all_different(S, E, N, D, M, O, R, Y) S E N D M O R Y MSORM 2000 {1. . 9} {0. . 9} Constraint Programming Tutorial 34

Basic Constraints and Propagators 1000*S + 100*E + 10*N + D + 1000*M + 100*O + 10*R + E = 10000*M + 1000*O + 100*N + 10*E + Y all different(S, E, N, D, M, O, R, Y) S E N D M O R Y MSORM 2000 {1. . 9} {0. . 9} {1} {0. . 9} Constraint Programming Tutorial 35

Basic Constraints and Propagators 1000*S + 100*E + 10*N + D + 1000*M + 100*O + 10*R + E = 10000*M + 1000*O + 100*N + 10*E + Y all different(S, E, N, D, M, O, R, Y) S E N D M O R Y MSORM 2000 {2. . 9} {0, 2. . 9} {1} {0, 2. . 9} Constraint Programming Tutorial 36

Basic Constraints and Propagators 1000*S + 100*E + 10*N + D + 1000*M + 100*O + 10*R + E = 10000*M + 1000*O + 100*N + 10*E + Y all different(S, E, N, D, M, O, R, Y) S E N D M O R Y MSORM 2000 {2. . 9} {0, 2. . 9} {1} {0, 2. . 9} and so on Constraint Programming Tutorial 37

Basic Constraints and Propagators 1000*S + 100*E + 10*N + D + 1000*M + 100*O + 10*R + E = 10000*M + 1000*O + 100*N + 10*E + Y all different(S, E, N, D, M, O, R, Y) S E N D M O R Y MSORM 2000 {9} {5. . 7} {6. . 8} {2. . 8} {1} {0} {2. . 8} Constraint Programming Tutorial 38

Issues in Propagation h Expressivity: What kind of information can be expressed as propagators? h Completeness: What behavior can be expected from propagation? h Efficiency: How much computational resources does propagation consume? MSORM 2000 Constraint Programming Tutorial 39

Completeness of Propagation h Given: Basic constraint C and propagator P. h Propagation is complete, if for every variable x and every value v in the domain of x, there is an assignment in which x=v that satisfies C and P. h Complete propagation is also called domain-consistency or arc-consistency. MSORM 2000 Constraint Programming Tutorial 40

Completeness of Propagation h General arithmetic constraints are undecidable (Hilbert’s Tenth Problem). h Propagation cannot always exhibit all inconsistencies. h Example: c 1: c 2: MSORM 2000 n > 2 a n + bn = cn Constraint Programming Tutorial 41

Example: Complete All Different w {1, 2, 3, 4} x { 2, 3, 4} y { 2, 3, 4} z { 2, 3, 4} h P: all_different(w, x, y, z) h C: MSORM 2000 Constraint Programming Tutorial 42

Example: Complete All Different w {1, 2, 3, 4} x { 2, 3, 4} y { 2, 3, 4} z { 2, 3, 4} h P: all_different(w, x, y, z) h C: h Most efficient known algorithm: O(|X|2 dmax 2) Regin [1994], using graph matching MSORM 2000 Constraint Programming Tutorial 43

Basic Constraints vs. Propagators h. Basic constraints hare conjunctions of constraints of the form X S, where S is a finite set of integers h. Enjoy complete constraint solving h. Propagators hcan be arbitrarily expressive (arithmetic, symbolic) himplementation typically fast but incomplete MSORM 2000 Constraint Programming Tutorial 44

Propagation vs Branching Obvious trade-off: Complex propagation algorithms result in fewer, but more expensive nodes in the search tree. Example: MONEY with alldiff and sum: only test fixed assignment MSORM 2000 alldiff: wait for fixed variables sum: interval cons. alldiff and sum: domain consistency Constraint Programming Tutorial 45

Some Propagator Classes h Symbolic propagators h Arithmetic propagators h Scheduling propagators h Reification MSORM 2000 Constraint Programming Tutorial 46

Symbolic Propagators Example: The “Element” Propagator Oz: {FD. element I Vector X} Meaning: X is the Ith element of Array Example: A = [5 6 7 8] I {0, 9} X {0, 9} Propagation in both directions: I {1, 3} X {5, 7} X {7} I {4} MSORM 2000 Constraint Programming Tutorial 47

Arithmetic Propagators General arithmetic equations: I 1*X 11*…*X 1 m 1 + … + In*Xn 1*…*Xnmn =: 0 <: MSORM 2000 >: =<: >=: =: Constraint Programming Tutorial 48

Scheduling Propagators Details later. Scheduling constraint classes: h resource constraints h precedence constraints MSORM 2000 Constraint Programming Tutorial 49

Reified Constraints Reflecting the validity of a constraint in a 0/1 variable Example: Reified arithmetic equations X = (I 1*X 11*…*X 1 m 1 + … + In*Xn 1*…*Xnmn =: 0) <: MSORM 2000 >: =<: >=: Constraint Programming Tutorial =: 50

Excursion: From Propagation to Problem Solving see Part II MSORM 2000 Constraint Programming Tutorial 51

Branching Algorithms Constraint programming systems provide h libraries of predefined branching algorithms h programming support for user-defined branching algorithms MSORM 2000 Constraint Programming Tutorial 52

Branching for MONEY proc {Money Root} S E N D M O R Y in Root=sol(s: S e: E n: N d: D m: M o: O r: R Root : : : 0#9 {FD. distinct Root} S =: 0 M =: 0 1000*S + 100*E + 10*N + + 1000*M + 100*O + 10*R + =: 10000*M + 1000*O + 100*N + 10*E + {FD. distribute ff Root} end {Explore. All Money} MSORM 2000 y: Y) Modeling D E Y Propagation Branching Exploration Constraint Programming Tutorial 53

Basic Choice Points choice x <: y [] x >=: y end x < y MSORM 2000 x >= y Constraint Programming Tutorial 54

Choice Point Sequences choice x <: y [] x >=: y end choice z = 1 [] z = 2 end x <: y z = 1 MSORM 2000 z = 2 x >=: y z = 1 z = 2 Constraint Programming Tutorial 55

Examples of Branching Algorithms h Enumeration: Choose variable, choose value h naive enumeration: choose variables and values in a fixed sequence h first-fail enumeration: choose a variable with minimal domain size h Domain-splitting: choice X <: Mid [] X >=: Mid end h Task MSORM 2000 sequencing for scheduling (later) Constraint Programming Tutorial 56

Excursion: Branching Algorithms in Oz see Part II MSORM 2000 Constraint Programming Tutorial 57

Exploration Algorithms Combinations of aspects such as: h Order of exploration h Interaction h Optimization h Visualization MSORM 2000 Constraint Programming Tutorial 58

Exploration for MONEY proc {Money Root} S E N D M O R Y in Root=sol(s: S e: E n: N d: D m: M o: O r: R Root : : : 0#9 {FD. distinct Root} S =: 0 M =: 0 1000*S + 100*E + 10*N + + 1000*M + 100*O + 10*R + =: 10000*M + 1000*O + 100*N + 10*E + {FD. distribute ff Root} end {Explore. All Money} MSORM 2000 y: Y) Modeling D E Y Propagation Branching Exploration Constraint Programming Tutorial 59

Order of Exploration h Depth-first search h Iterative Deepening h Limited discrepancy search [Harvey/Ginsberg 95] MSORM 2000 Constraint Programming Tutorial 60

Interaction h First-solution search h All solution search h Last solution search h Search with user interaction MSORM 2000 Constraint Programming Tutorial 61

Optimization h Branch-and-bound h Restart MSORM 2000 optimization Constraint Programming Tutorial 62

Visualization Example: Oz Explorer [Schulte 1997] Oz Explorer combines hvisualization hfirst/all solution / user interaction hbranch-and-bound optimization hdepth-first search MSORM 2000 Constraint Programming Tutorial 63

Excursion: Exploration Algorithms in Oz see Part II MSORM 2000 Constraint Programming Tutorial 64

Overview h Constraint Programming in a Nutshell h Elements of Constraint Programming h Case study: ACC 97/98 Basketball h Excursions: Constraint Programming in Oz h Constraint Programming Techniques h Constraint-based Scheduling MSORM 2000 Constraint Programming Tutorial 65

ACC 1997/98: A Success Story of Constraint Programming h Integer programming + enumeration, 24 hours Nemhauser, Trick: Scheduling a Major College Basketball Conference, Operations Research, January 1998, 46(1) h Constraint programming, less than 1 minute Henz: Scheduling a Major College Basketball Conference - Revisited, Operations Research, January 2001, 49(1) MSORM 2000 Constraint Programming Tutorial 66

Round Robin Tournament Planning Problems hn teams, each playing a fixed number of times r against every other team h r = 1: single, r = 2: double round robin. h Each match is home match for one and away match for the other h Dense round robin: h At each date, each team plays at most once. h The number of dates is minimal. MSORM 2000 Constraint Programming Tutorial 67

The ACC 1997/98 Problem h 9 teams participate in tournament h Dense double round robin: h there are 2 * 9 dates h at each date, each team plays either home, away or has a “bye” h Alternating MSORM 2000 weekday and weekend matches Constraint Programming Tutorial 68

The ACC 1997/98 Problem (cont’d) h No team can play away on both last dates. h No team may have more than two away matches in a row. h No team may have more than two home matches in a row. h No team may have more than three away matches or byes in a row. h No team may have more than four home matches or byes in a row. MSORM 2000 Constraint Programming Tutorial 69

The ACC 1997/98 Problem (cont’d) h Of the weekends, each team plays four at home, four away, and one bye. h Each team must have home matches or byes at least on two of the first five weekends. h Every team except FSU has a traditional rival. The rival pairs are Clem-GT, Duke-UNC, UMDUVA and NCSt-Wake. In the last date, every team except FSU plays against its rival, unless it plays against FSU or has a bye. MSORM 2000 Constraint Programming Tutorial 70

The ACC 1997/98 Problem (cont’d) h The following pairings must occur at least once in dates 11 to 18: Duke-GT, Duke-Wake, GTUNC, UNC-Wake. h No team plays in two consecutive dates away against Duke and UNC. No team plays in three consecutive dates against Duke UNC and Wake. h UNC plays Duke in last date and date 11. h UNC plays Clem in the second date. h Duke has bye in the first date 16. MSORM 2000 Constraint Programming Tutorial 71

The ACC 1997/98 Problem (cont’d) h Wake does not play home in date 17. h Wake has a bye in the first date. h Clem, Duke, UMD and Wake do not play away in the last date. h Clem, FSU, GT and Wake do not play away in the fist date. h Neither FSU nor NCSt have a bye in the last date. h UNC does not have a bye in the first date. MSORM 2000 Constraint Programming Tutorial 72

Nemhauser/Trick Solution h Enumerate h explicit enumeration (very fast) h Compute h integer MSORM 2000 abstract schedules [Schreuder 1992] programming (several minutes) h Compute h explicit pattern sets programming (below 1 minute) h Compute h integer home/away/bye patterns concrete schedules enumeration (approx. 24 hours) Constraint Programming Tutorial 73

Constraint Programming Solution h Enumerate h constraint h Compute programming (very fast) pattern sets h constraint h Assign home/away/bye patterns programming (below 10 seconds) teams to patterns h constraint h Compute concrete schedules h constraint MSORM 2000 programming (below 30 seconds) programming (below 20 seconds) Constraint Programming Tutorial 74

Modeling ACC 97/98 as Constraint Satisfaction Problem Variables h 9 * 18 variables taking values from {0, 1} that express which team plays home when. Example: HUNC, 5=1 means UNC plays home on date 5. h away, bye similar, e. g. AUNC, 5 or BUNC, 5 h 9 * 18 variables taking values from {0, 1, . . . , 9} that express against which team which other team plays. Example: UNC, 5 =1 means UNC plays team 1 (Clem) on date 5 MSORM 2000 Constraint Programming Tutorial 75

Assessment h Naive branching algorithm suffices h Naive exploration algorithm suffices h Mission-critical component: Propagation algorithms! h Element propagator for assigning patterns to teams h All-different propagator for opponents in one season h Symmetric all-different propagator for opponents in one round h More references (see www. comp. nus. edu. sg/~henz) h Constraint-based Round Robin Scheduling, ICLP 99 h Global Constraints for Round Robin Tournaments, draft MSORM 2000 Constraint Programming Tutorial 76

Friar Tuck h Constraint programming tool for sport scheduling, ACC 97/98 just one instance h Used by sports leagues in US and Europe h Convenient entry of constraints through GUI h Friar Tuck 1. 1 available for Unix and Windows 95/98 (www. comp. nus. edu. sg/~henz/projects/Friar. Tuck) h Implementation language: Oz using Mozart Friar Tuck Demo MSORM 2000 Constraint Programming Tutorial 77

Overview h Constraint I II Programming in a Nutshell h Elements of Constraint Programming h Case study: ACC 97/98 Basketball h Concluding Part I h Excursions: Constraint Programming in Oz h Constraint Programming Techniques h Constraint-based Scheduling MSORM 2000 Constraint Programming Tutorial 78

Assessment: Don’t Use It! Don’t use constraint programming for: h Problems for which there are known efficient algorithms or heuristics. Example: Traveling salesman. h Problems for which integer programming works well, such as many discrete assignment problems. h Problems with weak constraints and a complex optimization function, such as many timetabling problems. MSORM 2000 Constraint Programming Tutorial 79

Assessment: Do Use It! Use constraint programming for: h Problems for which integer programming does not work (linear models too large) and for which there are no efficient heuristic solutions available. h Problems with tight constraints, where propagation can be employed. Example: ACC 97/98. h Problems for which strong branching algorithms exist. Example: Scheduling with unary resources. h Problems that need customized branching or search algorithms, extensive performance debugging or tight software integration MSORM 2000 Constraint Programming Tutorial 80

Myths Debunked h. A fad! Constraint programming has been used successfully in a number of application areas, most spectacularly in scheduling h Universal! More failure stories than success stories. h All new! Many ideas come from AI search and Operations Research. In particular, the important ideas for scheduling come from OR. h Artificial Intelligence! Mostly quite earthly algorithms. Constraint programming systems provide software framework for these algorithms to interact with each other. MSORM 2000 Constraint Programming Tutorial 81

The Future h Constraint programming will become a standard technique in OR for solving combinatorial problems, along with local search and integer programming. h Constraint programming techniques will be tightly integrated with integer programming and local search. h Specific propagation algorithms will be developed to cater for important application domains. MSORM 2000 Constraint Programming Tutorial 82

Overview h Constraint Programming in a Nutshell h Elements of Constraint Programming h Case study: ACC 97/98 Basketball h Excursions: Constraint Programming in Oz h Constraint Programming Techniques h Constraint-based Scheduling MSORM 2000 Constraint Programming Tutorial 83

Excursion: From Propagation to Problem Solving Start Oz Programming Interface MSORM 2000 Constraint Programming Tutorial 84

Excursion: Branching Algorithms in Oz Start Oz Programming Interface MSORM 2000 Constraint Programming Tutorial 85

Excursion: Exploration Algorithms in Oz Start Oz Programming Interface MSORM 2000 Constraint Programming Tutorial 86

Overview h Constraint Programming in a Nutshell h Elements of Constraint Programming h Case study: ACC 97/98 Basketball h Excursions: Constraint Programming in Oz h Constraint Programming Techniques h Constraint-based Scheduling MSORM 2000 Constraint Programming Tutorial 87

Constraint Programming Techniques h Symmetry Breaking h Redundant Constraints h Parameterized Problems MSORM 2000 Constraint Programming Tutorial 88

Symmetry Breaking Often, the most efficient model admits many different solutions that are essentially the same (“symmetric” to each other). Symmetry breaking tries to improve the performance of search by eliminating such symmetries. MSORM 2000 Constraint Programming Tutorial 89

Redundant Constraints h Pruning of original model is often not sufficient h Adding redundant constraints sometimes helps MSORM 2000 Constraint Programming Tutorial 90

Example: Grocery Puzzle A kid goes into a grocery store and buys four items. The cashier charges $7. 11. The kid pays and is about to leave when the cashier calls the kid back, and says “Hold on, I multiplied the four items instead of adding them; I’ll try again… Gosh, with adding them the price still comes to $7. 11”! What were the prices of the four items? MSORM 2000 Constraint Programming Tutorial 91

Model for Grocery Puzzle h Variables A, B, C, D represent prices of items in cents. h Constraints: h. A + B + C + D = 711 h A * B * C * D = 711 * 100 MSORM 2000 Constraint Programming Tutorial 92

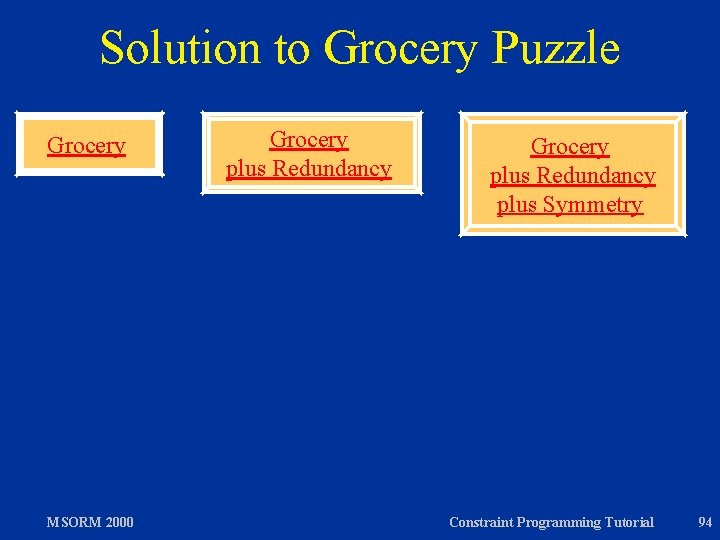
Additional Constraints h Redundant constraint 79 is prime factor of 711. Thus without loss of generality: A divisible by 79. h Symmetries B C D MSORM 2000 Constraint Programming Tutorial 93

Solution to Grocery Puzzle Grocery MSORM 2000 Grocery plus Redundancy plus Symmetry Constraint Programming Tutorial 94

Example: Fractions Find distinct non-zero digits such that the following equation holds: A D + B C MSORM 2000 G + E F = 1 H I Constraint Programming Tutorial 95

Model for Fractions h One variable for each letter, similar to MONEY h Constraint A*E*F*H*I + D*B*C*H*I + G*B*C*E*F = MSORM 2000 B*C*E*F*H*I Constraint Programming Tutorial 96

Additional Constraints h Symmetries A D B C h Redundant constraints E F A 3 * G H I 1 B C G 3 * 1 H I MSORM 2000 Constraint Programming Tutorial 97

Fractions plus Symmetries h Constraint A*E*F*H*I + D*B*C*H*I + G*B*C*E*F = B*C*E*F*H*I h Symmetries A*E*F >= D*B*C D*H*I >= G*E*F h Redundant Constraints 3*A >= B*C 3*G =< H*I MSORM 2000 Fractions plus Symmetries plus Redundancies Constraint Programming Tutorial 98

Redundant Constraints Adding redundant constraints sometimes results in dramatic performance improvements. MSORM 2000 Constraint Programming Tutorial 99

Performance of Symmetry Breaking h All solution search: Symmetry breaking usually improves performance; often dramatically h One solution search: Symmetry breaking may or may not improve performance MSORM 2000 Constraint Programming Tutorial 100

Parameterized Problems h Modeling facilities in Oz are embedded in advanced programming language. h Problem scripts can be result of computation. h Applications: h Embedding problem solving in complex applications h Parameterized problems Excursion: N Queens MSORM 2000 Start Oz Programming Interface Constraint Programming Tutorial 101

Overview h Constraint Programming in a Nutshell h Elements of Constraint Programming h Case study: ACC 97/98 Basketball h Excursions: Constraint Programming in Oz h Constraint Programming Techniques h Constraint-based Scheduling MSORM 2000 Constraint Programming Tutorial 102

Review Constraint programming is a framework for integrating three families of algorithms h Propagation algorithms h Branching algorithms h Exploration algorithms MSORM 2000 Constraint Programming Tutorial 103

E=4 S E N D M O R Y {9} {4. . 7} {5. . 8} {2. . 8} {1} {0} {2. . 8} E 4 E=5 S E N D M O R Y {9} {5. . 7} {6. . 8} {2. . 8} {1} {0} {2. . 8} {9} {5} {6} {7} {1} {0} {8} {2} E=6 MSORM 2000 S E N D + M O R E = M O N E Y E 5 S E N D M O R Y {9} {6. . 7} {7. . 8} {2. . 8} {1} {0} {2. . 8} E 6 Constraint Programming Tutorial 104

Optimization h Modeling: define optimization function h Propagation algorithms: identify propagation algorithms for optimization function h Branching algorithms: identify branching algorithms that lead to good solutions early h Exploration algorithms: extend existing exploration algorithms to achieve optimization MSORM 2000 Constraint Programming Tutorial 105

Optimization: Example SEND + MOST MSORM 2000 = MONEY Constraint Programming Tutorial 106

SEND + MOST = MONEY Assign distinct digits to the letters S, E, N, D, M, O, T, Y such that S E N D + M O S T = M O N E Y holds and M O N E Y is maximal. MSORM 2000 Constraint Programming Tutorial 107

Modeling Formalize the problem as a constraint optimization problem: h Number of variables: n h Constraints: c 1, …, cm n n n h Optimization constraints: d 1, …, dm 2 Given a solution a, and an optimization constraint di , the constraint di(a) n contains only assignments that are better than a. MSORM 2000 Constraint Programming Tutorial 108

A Model for MONEY h number of variables: 8 h constraints: c 1 = {(S, E, N, D, M, O, T, Y) c 2 = {(S, E, N, D, M, O, T, Y) 1000*S + 1000*M = 10000*M + 1000*O MSORM 2000 8 8 + + + | 0 | 100*E 100*O 100*N S, …, Y 9 } + 10*N + D + 10*S + T + 10*E + Y} Constraint Programming Tutorial 109

A Model for MONEY (continued) h more constraints c 3 = {(S, E, N, D, M, O, T, Y) 8 | S 0 } c 4 = {(S, E, N, D, M, O, T, Y) 8 | M 0 } c 5 = {(S, E, N, D, M, O, T, Y) 8 | S…Y all different} h optimization constraint: d : (s, e, n, d, m, o, t, y) {(S, E, N, D, M, O, T, Y) 8 | 10000*m + 1000*o + 100*n + 10*e + y < 10000*M + 1000*O + 100*N + 10*E + Y } MSORM 2000 Constraint Programming Tutorial 110

Propagation Algorithms Identify a propagation algorithm to implement the optimization constraints Example: SEND + MOST = MONEY d : (s, e, n, d, m, o, t, y) {(S, E, N, D, M, O, T, Y)) 8 8 | 10000*m + 1000*o + 100*n + 10*e + y < 10000*M + 1000*O + 100*N + 10*E + Y } Given a solution a, choose propagation algorithm for d(a). MSORM 2000 Constraint Programming Tutorial 111

Branching Algorithms Identify a branching algorithm that finds good solutions early. Example: SEND + MOST = MONEY Idea: Naive enumeration in the order M, O, N, E, Y. Try highest values first. MSORM 2000 Constraint Programming Tutorial 112

Exploration Algorithms Modify exploration such that for each solution a, corresponding optimization constraints are added. Two strategies: h branch-and-bound: continue as in original exploration h restart optimization: after each solution, start from the root. MSORM 2000 Constraint Programming Tutorial 113

Using Oz proc {Money Root} S E N D M O R Y in Root=sol(s: S e: E n: N d: D m: M o: O r: R y: Y) Root : : : 0#9 {FD. distinct Root} S =: 0 M =: 0 1000*S + 100*E + 10*N + D + 1000*M + 100*O + 10*R + E =: 10000*M + 1000*O + 100*N + 10*E + Y {FD. distribute ff Root} end proc {Optimization. Constraint Old New} sol(s: S 1 e: E 1 n: N 1 d: D 1 m: M 1 o: O 1 t: T 1 y: Y 1) = Old sol(s: S 2 e: E 2 n: N 2 d: D 2 m: M 2 o: O 2 t: T 2 y: Y 2) = New in 10000*M 1 + 1000*O 1 + 100*N 1 + 10*E 1 + Y 1 <: 10000*M 2 + 1000*O 2 + 100*N 2 + 10*E 2 + Y 2 end {Explorer. object script(Money Optimization. Constraint)} MSORM 2000 Constraint Programming Tutorial 114

Experiments with MONEY Search MONEY Optimization MSORM 2000 Constraint Programming Tutorial 115

Scheduling h Scheduling Problems h Propagation Algorithms for Resource Constraints h Branching Algorithms h Other Constraints h Exploration Algorithms h Literature MSORM 2000 Constraint Programming Tutorial 116

Scheduling Problems Assign starting times (and sometimes durations) to tasks, subject to h resource constraints, h precedence constraints, h idiosyncratic and other constraints, and h an optimization function, often to minimize overall schedule duration. MSORM 2000 Constraint Programming Tutorial 117

Example: Building a Bridge Animate Solution h Resource Show Constraints Gantt Chart constraints Example: a 1 and a 2 use excavator, cannot overlap in time h Precedence constraints Example: p 1 requires a 3, a 3 must end before p 1 starts MSORM 2000 Constraint Programming Tutorial 118

Modeling h Indices: Tasks = [beg a 1 a 2 a 3 a 4 a 5 a 6 p 1] h Constants: duration of tasks Duration = d(beg: 0 a 1: 4 a 2: 2. . . ) h Variables: represent each task with a finite domain variable representing its starting time. Start = {FD. record start Tasks 0#Max. Time} Start. t is finite domain variable representing the starting time of task t MSORM 2000 Constraint Programming Tutorial 119

Precedence Constraints For each two tasks t 1, t 2, where t 1 must precede t 2, introduce a constraint Start. t 1 + Duration. t 1 Start. t 2 MSORM 2000 Constraint Programming Tutorial 120

Resource Constraints For each two tasks t 1, t 2 that require a unary resource r, we have the constraint Start. t 1 + Duration. t 1 Start. t 2 + Duration. t 2 Start. t 1 But: many constraints and weak propagation. Thus, introduce global resource constraints. MSORM 2000 Constraint Programming Tutorial 121

Global Resource Constraints in Oz {Schedule. serialized. Disj [ [a 1 a 2 a 3 a 4 a 5 a 6] % excavator [p 1 p 2] % pile driver. . . ] Start Duration} User chooses among Schedule. serialized. Disj Schedule. task. Intervals MSORM 2000 Constraint Programming Tutorial 122

Propagation: Using Disjunction For all tasks t 1, t 2 using the same resource: Start. t 1 + Duration. t 1 Start. t 2 + Duration. t 2 Start. t 1 Weakest but fastest form of propagation for unary resources. MSORM 2000 Constraint Programming Tutorial 123

Propagation: Edge finding For a given task t and set of tasks S, all sharing the same unary resource , find out whether t can occur h before all tasks in S, h after all tasks in S, h between two tasks in S, and infer corresponding basic constraints. MSORM 2000 Constraint Programming Tutorial 124

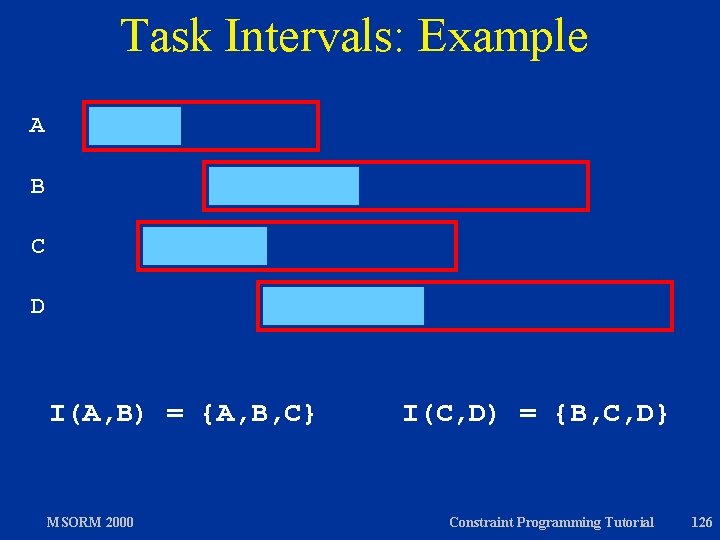
Propagation: Task Intervals Notation: est(t): earliest starting time lct(t): latest completion time For two tasks t 1 and t 2 where est(t 1) est(t 2) and lct(t 1) lct(t 2), the task interval I(t 1, t 2) is defined: I(t 1, t 2) = { t | est(t 1) est(t) and lct(t) lct(t 2) } Perform edge finding on all task intervals. MSORM 2000 Constraint Programming Tutorial 125

Task Intervals: Example A B C D I(A, B) = {A, B, C} MSORM 2000 I(C, D) = {B, C, D} Constraint Programming Tutorial 126

Which Edge Finder? As usual, trade-off between run-time of propagation algorithm and strength of propagation. Edge finding can be expensive depending on which tasks are considered. Recent edge finders have complexity n 2 for one propagation step, where n is the number of tasks using the resource. Edge finding based on task intervals can be stronger than these, but typically have complexity n 3. MSORM 2000 Constraint Programming Tutorial 127

Demo: Propagation for Unary Resources Bridge MSORM 2000 Constraint Programming Tutorial 128

Branching Algorithms: Serializers h Simple enumeration techniques such as first-fail are hopeless for scheduling. h Use unary resources to guide branching. h For two tasks t 1, t 2 sharing the same resource, use the constraints Start. t 1 + Duration. t 1 Start. t 2 and Start. t 2 + Duration. t 2 Start. t 1 for branching. MSORM 2000 Constraint Programming Tutorial 129

Which Tasks To Serialize? h Resource-oriented serialization: Serialize all tasks of one resource completely, before tasks of another resource are serialized. h Most-used-resource serialization h Global slack h Local slack h Task-oriented serialization: Choose two suitable tasks at a time, regardless of resources. h Slack-based MSORM 2000 task serialization (see later) Constraint Programming Tutorial 130

Most-used-resource Serialization “Most-used-resource” serialization: serialize first the resource that is used the most. Let T be a set of tasks running on resource r. demand(T) = t T Duration. t Let S be the set of all tasks using resource r. demand(r) : = demand(S) Serialize the resource r with maximal demand(r) first. MSORM 2000 Constraint Programming Tutorial 131

Slack-based Resource Serialization Let T be a set of tasks running on resource r. supply(T) = lct(T) - est(T) demand(T) = t T Duration. t slack(T) = supply(T) - demand(T) Let S be the set of all tasks using resource r. slack(r) : = slack(S), S is set of all task running on r. Global slack serialization: Serialize resource with smallest slack first MSORM 2000 Constraint Programming Tutorial 132

Local-Slack Resource Serialization Let Ir be all task intervals on r. The local slack is defined as min {slack(I) | I Ir} Local slack serialization: Serialize resource with smallest local slack first. Use global slack for tie -breaking. MSORM 2000 Constraint Programming Tutorial 133

Which Tasks Are Serialized? Ideas: h Use edge finding to look for possible first tasks (and last tasks) h Choose tasks according to their est, lst (lct, ect). MSORM 2000 Constraint Programming Tutorial 134

Task-oriented Serialization Among all tasks using all resources, select a pair of tasks according to local/global slack criteria and other considerations, regardless what resources are serialized already. Provides more fine-grained control at the expense of runtime for finding candidate task pairs among all tasks. MSORM 2000 Constraint Programming Tutorial 135

Demo: Serialization Algorithms Bridge MSORM 2000 Constraint Programming Tutorial 136

Exploration Algorithms h Usually: branch-and-bound using minimization of the starting time of a “last” task minimize a[end]. start subject to {. . . } h Lower-bounding: Prove the non-existence of a solution with Start. last n, add constraint Start. last > n; increase n by . h Upper-bounding: Find solution with Start. last = n, add constraint Start. last < n; decrease n by . MSORM 2000 Constraint Programming Tutorial 137

Literature on CP & Scheduling h Van Hentenryck: The OPL optimization programming language, 1999 h Constraint Programming Tutorial of Mozart, 2000 (www. mozart-oz. org) h Applegate, Cook: A computational study of the job -shop scheduling problem, 1991 h Carlier, Pinson: An algorithm for solving the jobshop scheduling problem, 1989 h Various papers by Laburthe, Caseau, Baptiste, Le Pape, Nuijten, see “Overview” paper MSORM 2000 Constraint Programming Tutorial 138

Overview h Constraint Programming in a Nutshell h Elements of Constraint Programming h Case study: ACC 97/98 Basketball h Constraint Programming Techniques h Excursions: Constraint Programming in Oz h Constraint-based Scheduling h Some Final Thoughts MSORM 2000 Constraint Programming Tutorial 139

Assessment: Don’t Use It! Don’t use constraint programming for: h Problems for which there are known efficient algorithms or heuristics. Example: Traveling salesman. h Problems for which integer programming works well, such as many discrete assignment problems. h Problems with weak constraints and a complex optimization function, such as many timetabling problems. MSORM 2000 Constraint Programming Tutorial 140

Assessment: Do Use It! Use constraint programming for: h Problems for which integer programming does not work (linear models too large) and for which there are no efficient solutions available. h Problems with tight constraints, where propagation can be employed. Example: ACC 97/98. h Problems for which strong branching algorithms exist. Example: Scheduling with unary resources. h Problems that need customized branching or search algorithms, extensive performance debugging or tight software integration MSORM 2000 Constraint Programming Tutorial 141

Myths Debunked h. A fad! Constraint programming has been used successfully in a number of application areas, most spectacularly in scheduling h Universal! More failure stories than success stories. h All new! Many ideas come from AI search and Operations Research. In particular, the important ideas for scheduling come from OR. h Artificial Intelligence! Mostly quite earthly algorithms. Constraint programming systems provide software framework for these algorithms to interact with each other. MSORM 2000 Constraint Programming Tutorial 142

The Future h Constraint programming will become a standard technique in OR for solving combinatorial problems, along with local search and integer programming. h Constraint programming techniques will be tightly integrated with integer programming and local search. h Specific propagation algorithms will be developed to cater for important application domains. MSORM 2000 Constraint Programming Tutorial 143