An Introduction to Constraint Programming in JChoco Constraint

An Introduction to Constraint Programming in JChoco

Constraint satisfaction • Constraint satisfaction problem (CSP) is a triple <V, D, C> where: – V is set of variables – Each X in V has set of values, D_X • Usually assume finite domain • {true, false}, {red, blue, green}, [0, 10], … – C is set of constraints Goal: find assignment of values to variables to satisfy all the constraints

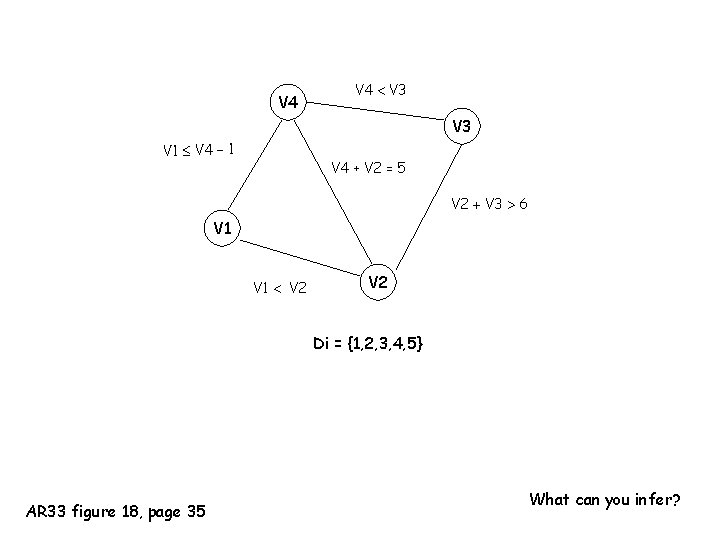
V 4 V 3 V 1 V 4 1 V 4 + V 2 = 5 V 2 V 3 6 V 1 V 2 Di = {1, 2, 3, 4, 5} AR 33 figure 18, page 35 What can you infer?

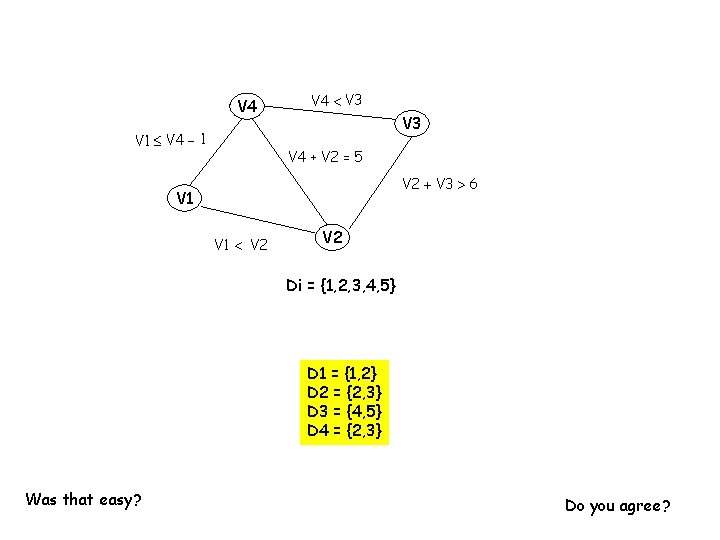
V 4 V 1 V 4 1 V 4 V 3 V 4 + V 2 = 5 V 2 V 3 6 V 1 V 2 Di = {1, 2, 3, 4, 5} D 1 = {1, 2} D 2 = {2, 3} D 3 = {4, 5} D 4 = {2, 3} Was that easy? Do you agree?

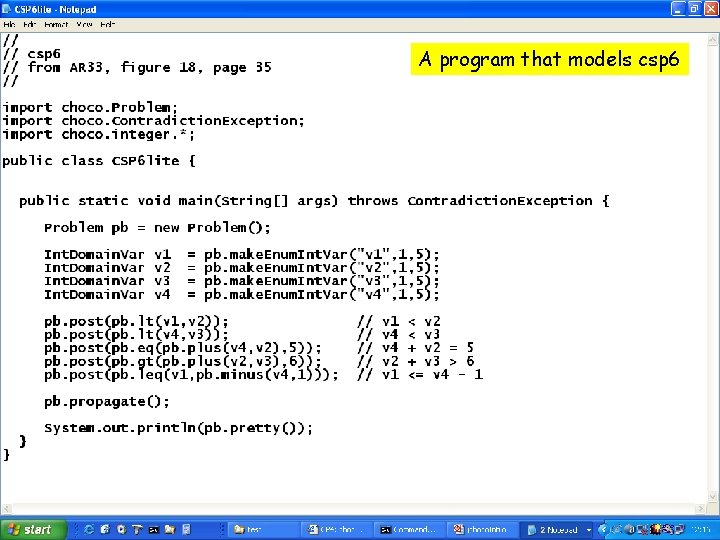
A program that models csp 6

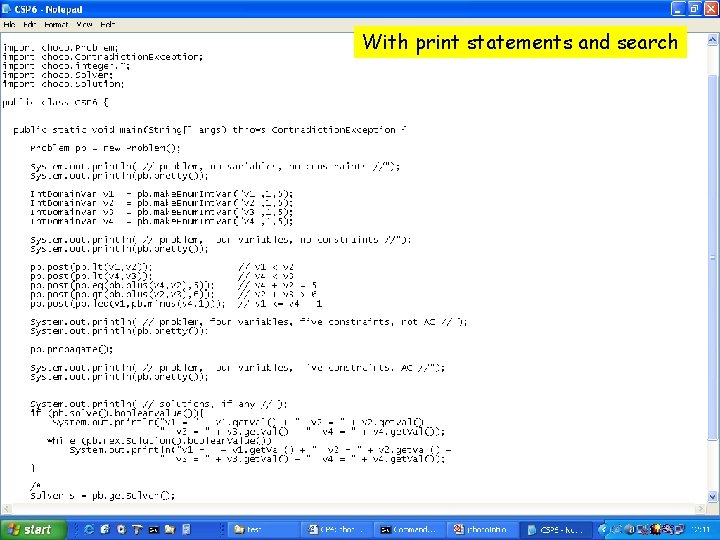
With print statements and search

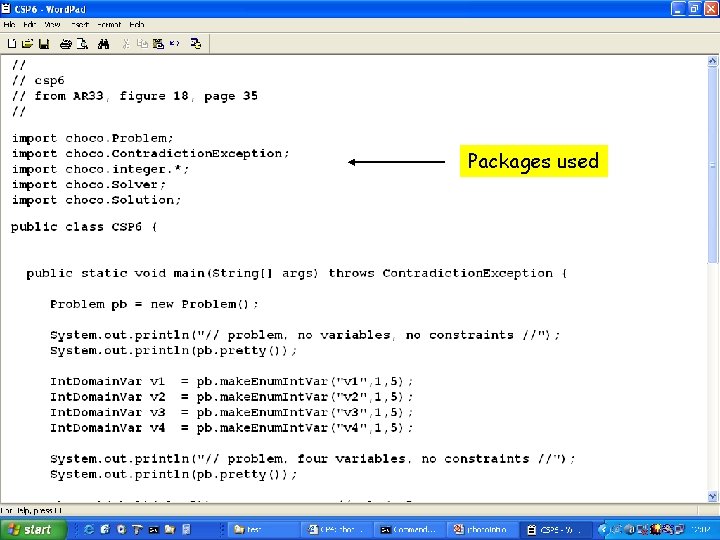
Packages used

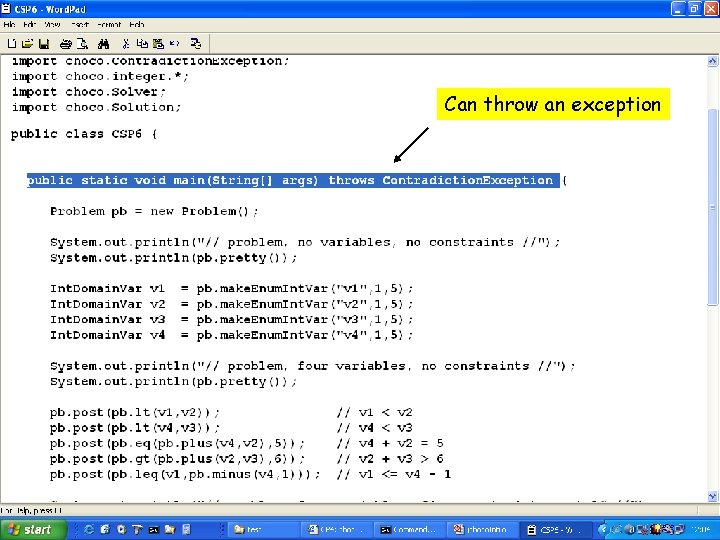
Can throw an exception

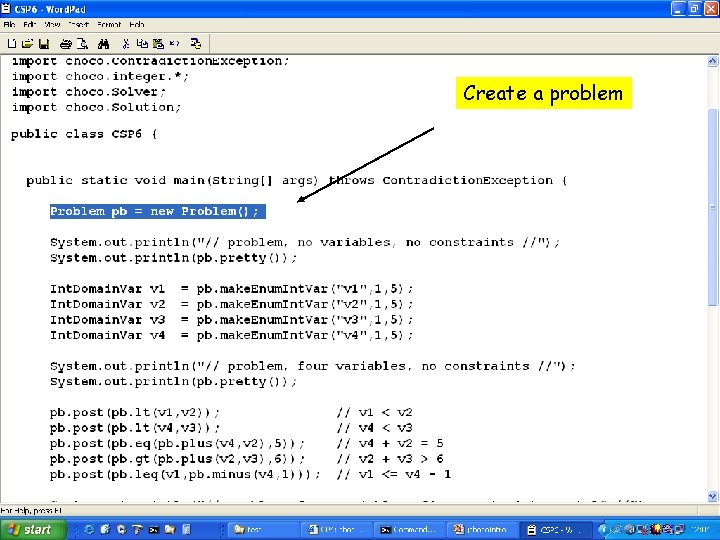
Create a problem

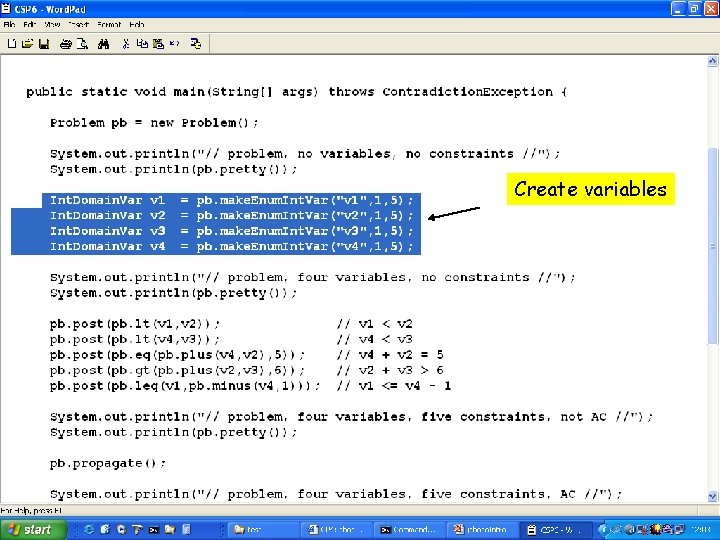
Create variables

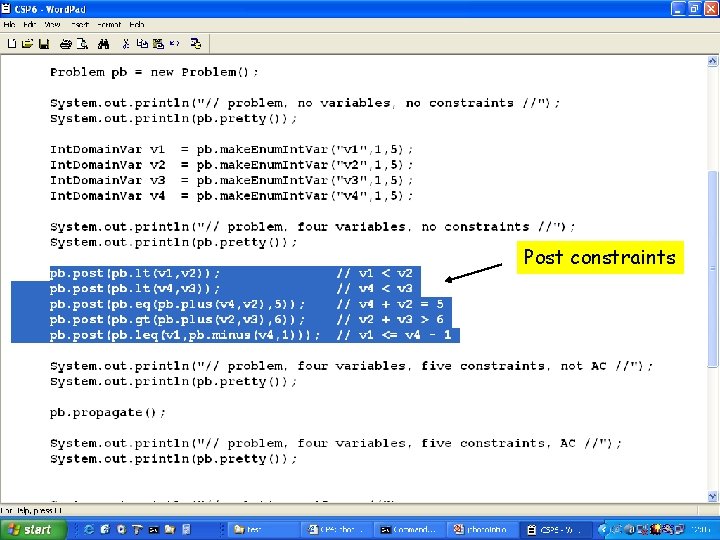
Post constraints

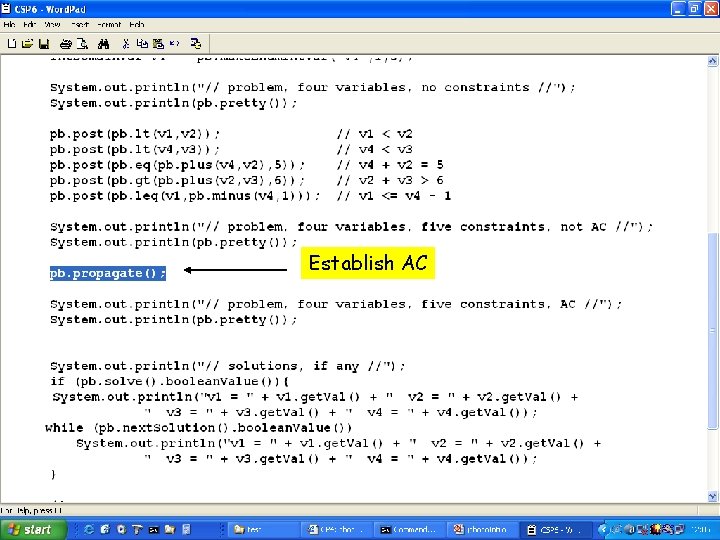
Establish AC

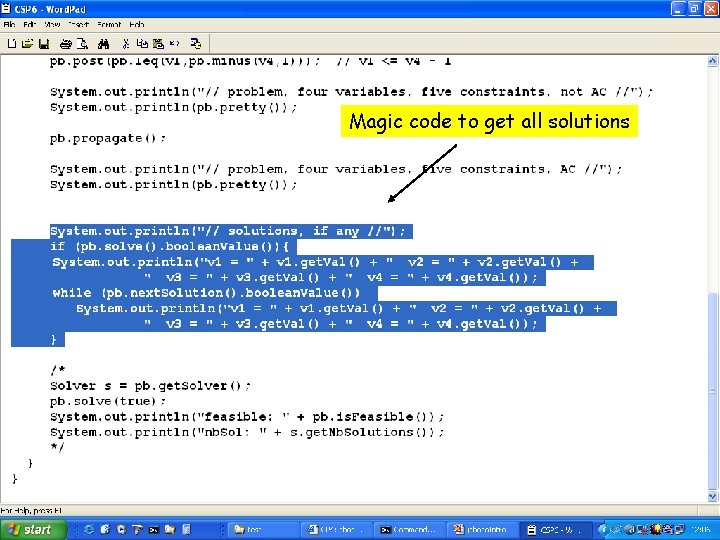
Magic code to get all solutions

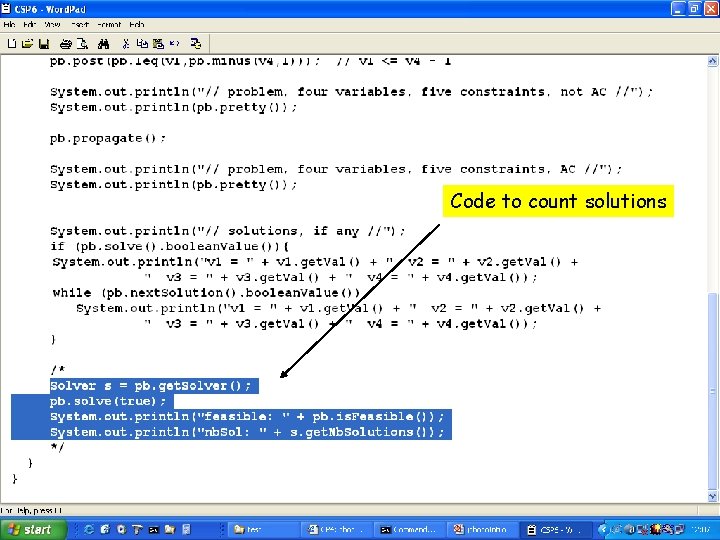
Code to count solutions

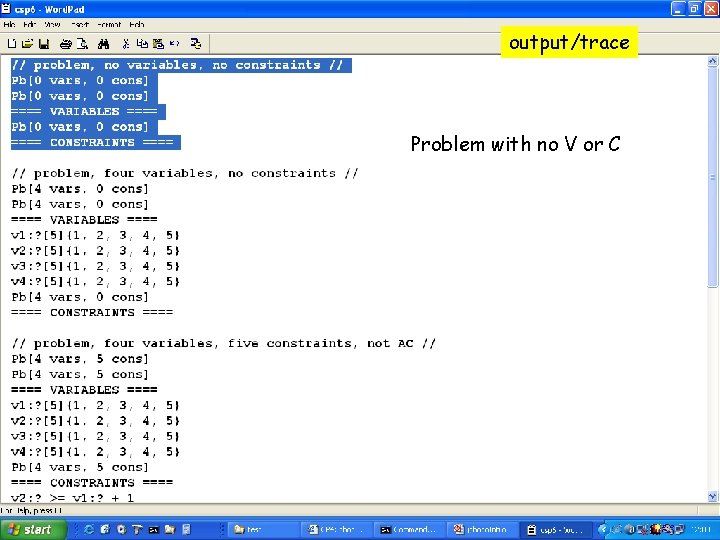
output/trace Problem with no V or C

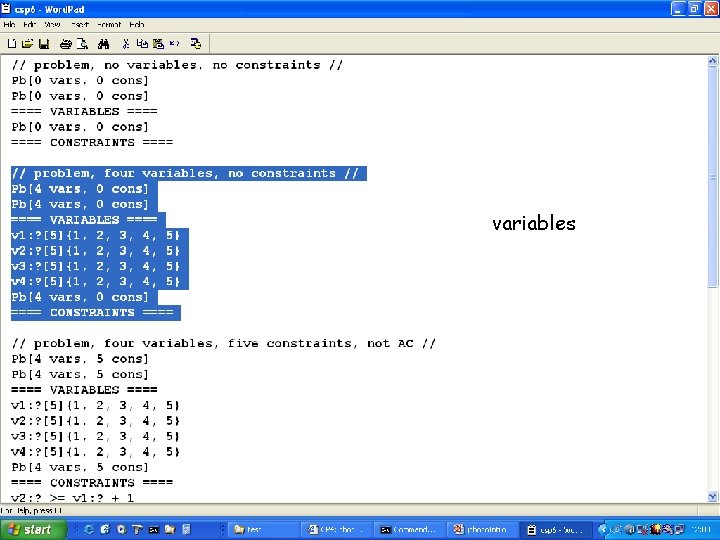
variables

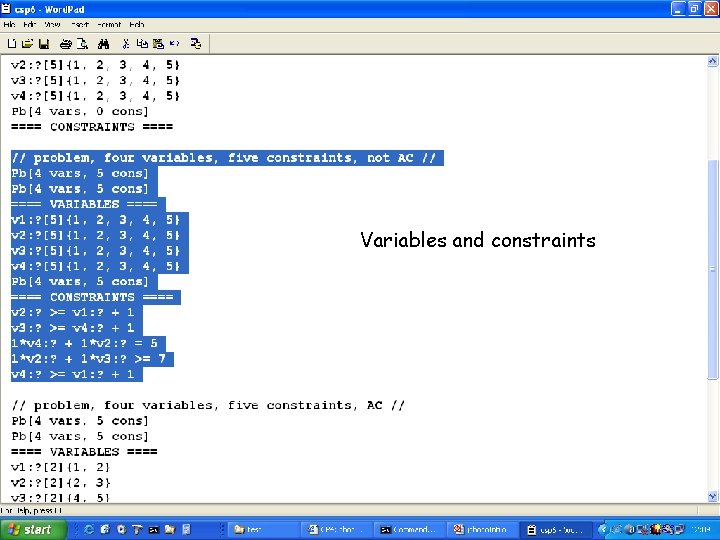
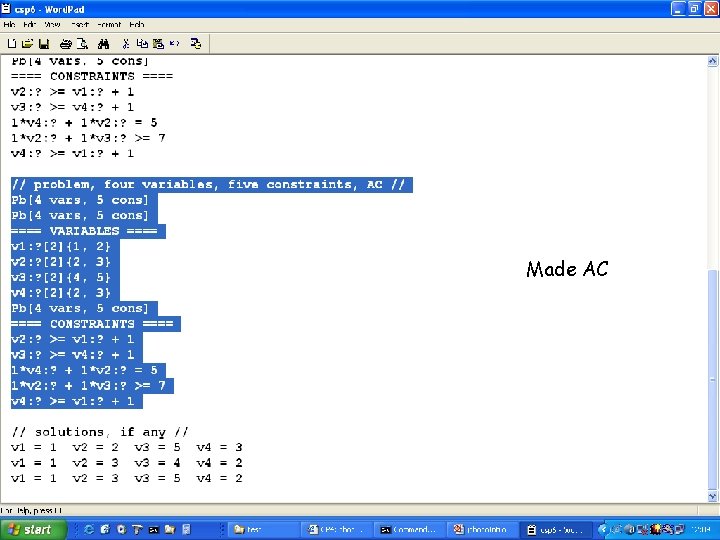
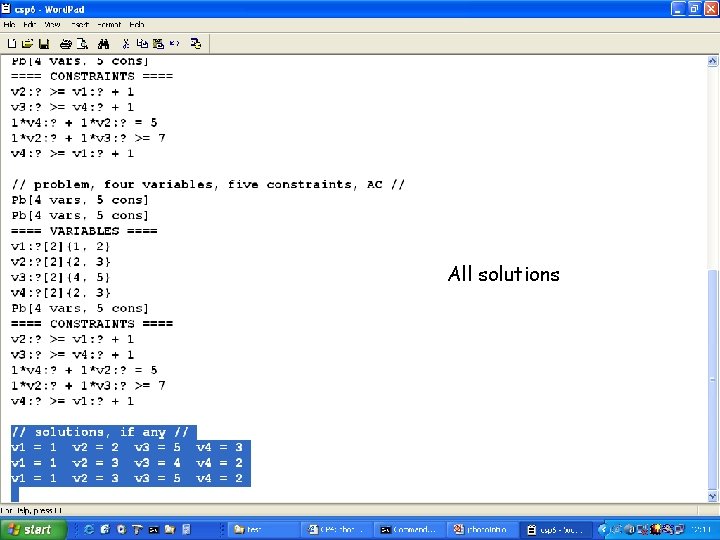
Variables and constraints

Made AC

All solutions

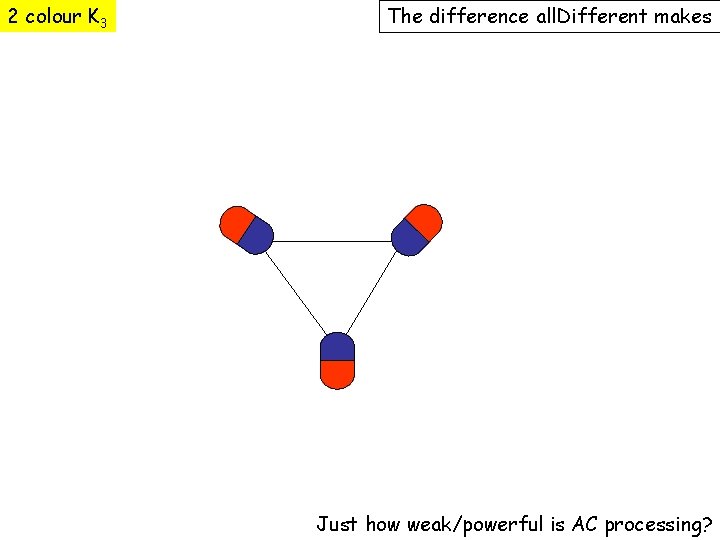
2 colour K 3 The difference all. Different makes Just how weak/powerful is AC processing?

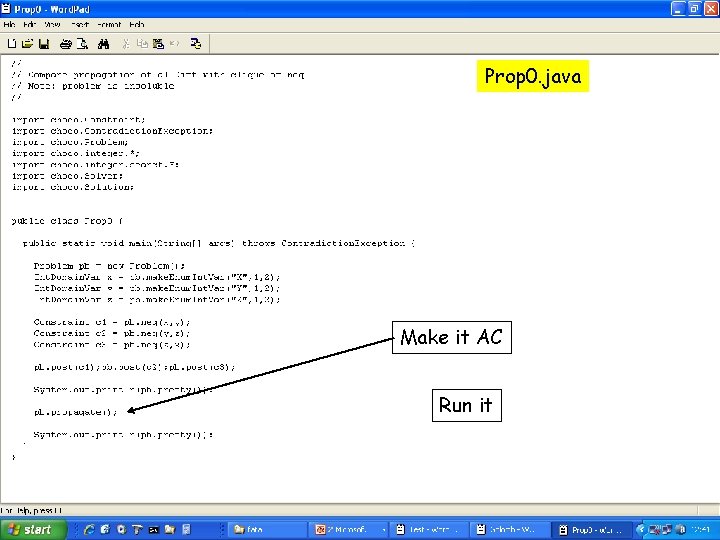
Prop 0. java Make it AC Run it

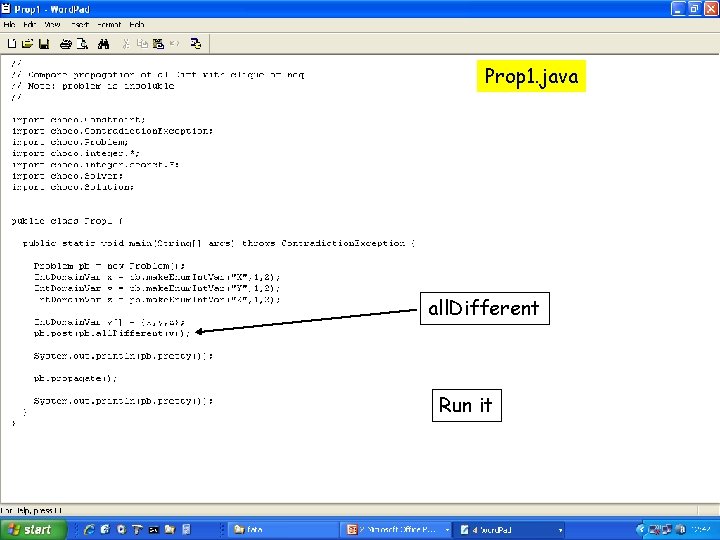
Prop 1. java all. Different Run it

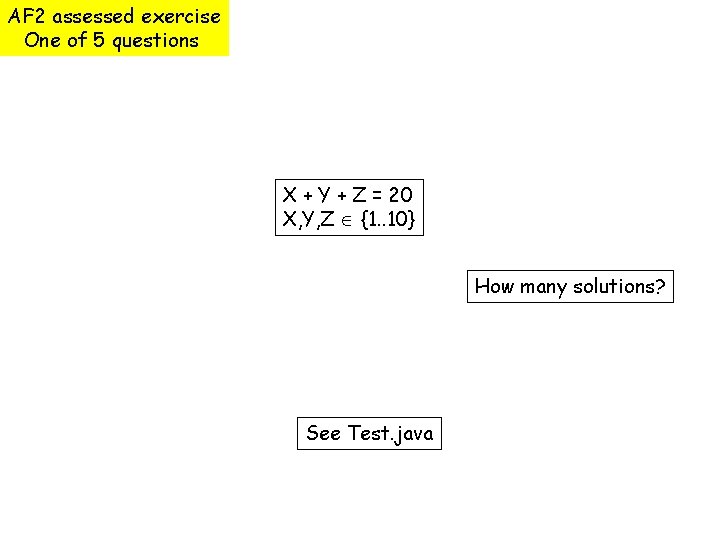
AF 2 assessed exercise One of 5 questions X + Y + Z = 20 X, Y, Z {1. . 10} How many solutions? See Test. java

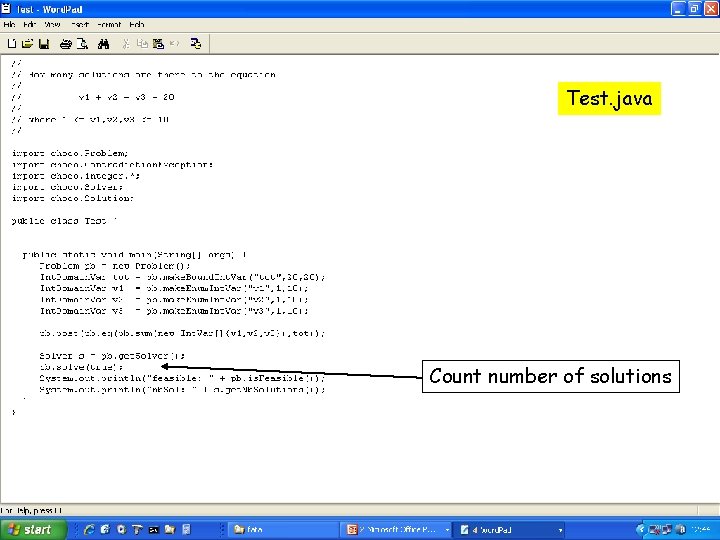
Test. java Count number of solutions

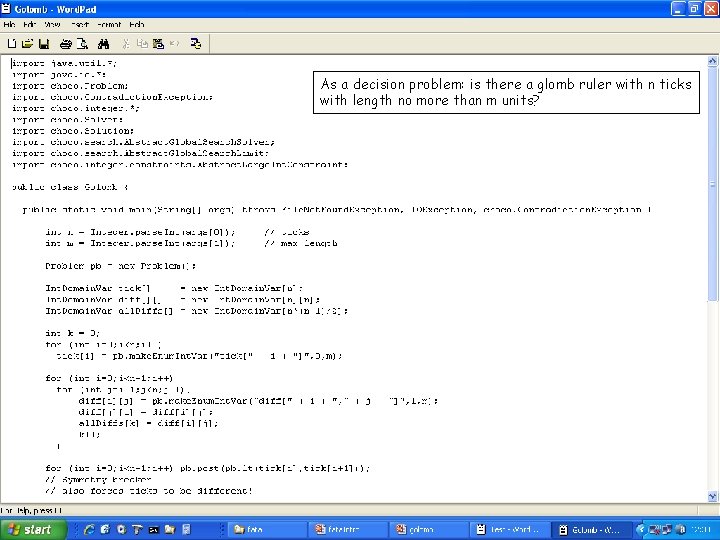
As a decision problem: is there a glomb ruler with n ticks with length no more than m units?

AF 2 assessed exercise How many n digit numbers are there where the number must contain at least 0 ne number 3 and at least one number 5? n=6 330095 501633 333335 120583 555355 … See Threes. And. Fives. java

Magic square An example of how to represent a problem An idea from Chris Beck

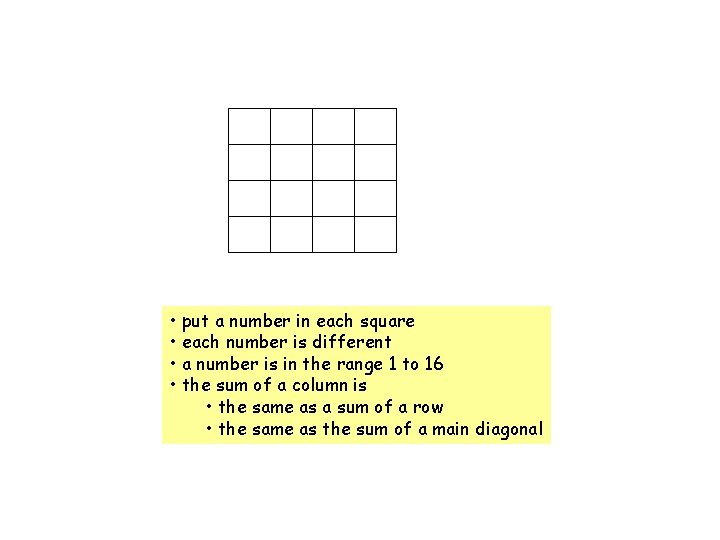
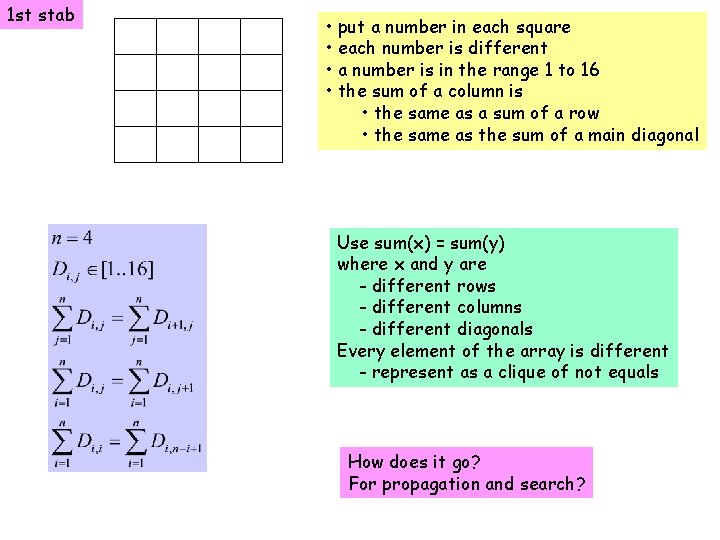
• put a number in each square • each number is different • a number is in the range 1 to 16 • the sum of a column is • the same as a sum of a row • the same as the sum of a main diagonal

1 st stab • put a number in each square • each number is different • a number is in the range 1 to 16 • the sum of a column is • the same as a sum of a row • the same as the sum of a main diagonal Use sum(x) = sum(y) where x and y are - different rows - different columns - different diagonals Every element of the array is different - represent as a clique of not equals How does it go? For propagation and search?

2 nd stab • put a number in each square • each number is different • a number is in the range 1 to 16 • the sum of a column is • the same as a sum of a row • the same as the sum of a main diagonal But what is k? How does model perform?

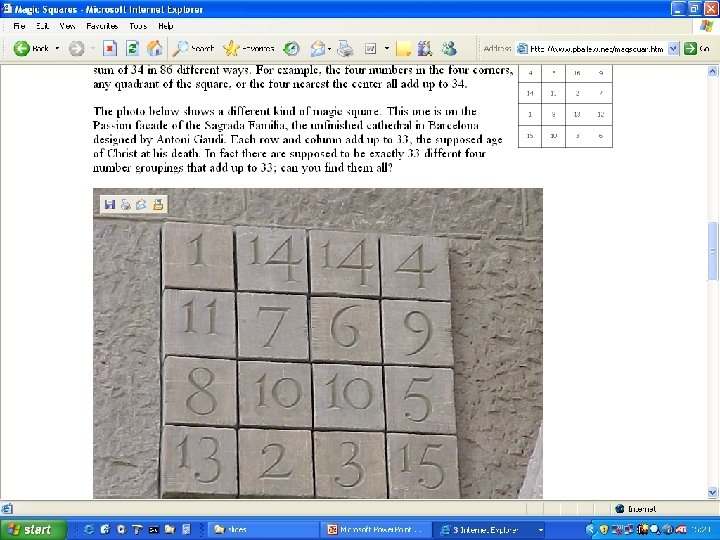
Magic square on the web http: //mathworld. wolfram. com/Magic. Square. html http: //mathforum. org/alejandre/magic. square. html

Thanks to Chris Beck

Thanks to Bouygues