Constraint processing An efficient alternative for search Constraint

























- Slides: 47

Constraint processing An efficient alternative for search

Constraint Processing: Overview ¤ Illustrating the idea with examples: è Numerical constraint nets, Spreadsheets ¤ Defining constraint problems ¤ Techniques for solving them: è A variety of backtracking techniques è Consistency and relaxation è Hybrid constraint techniques ¤ Some applications: è Understanding line drawings è Disambiguating natural language 2

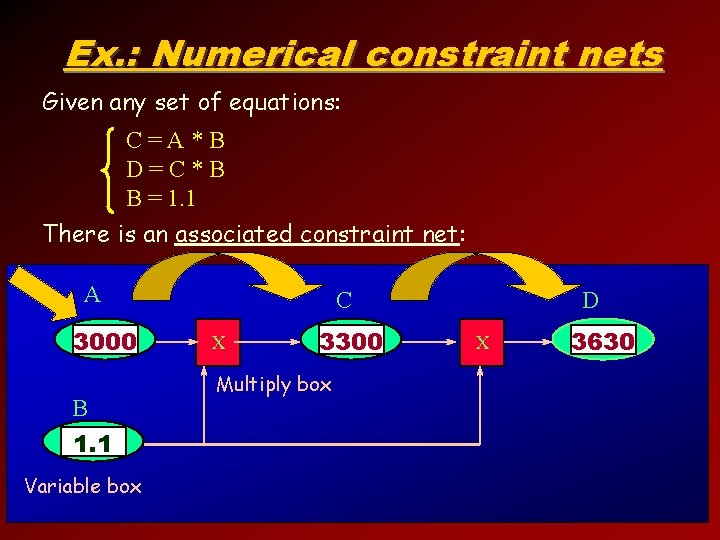
Ex. : Numerical constraint nets Given any set of equations: C=A*B D=C*B B = 1. 1 There is an associated constraint net: A 3000 B 1. 1 Variable box C X 3300 Multiply box D X 3630

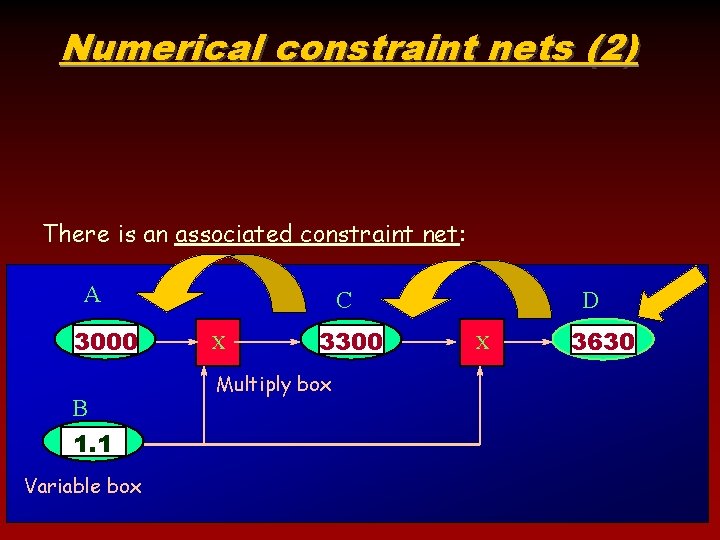
Numerical constraint nets (2) There is an associated constraint net: A 3000 B 1. 1 Variable box C X 3300 Multiply box D X 3630

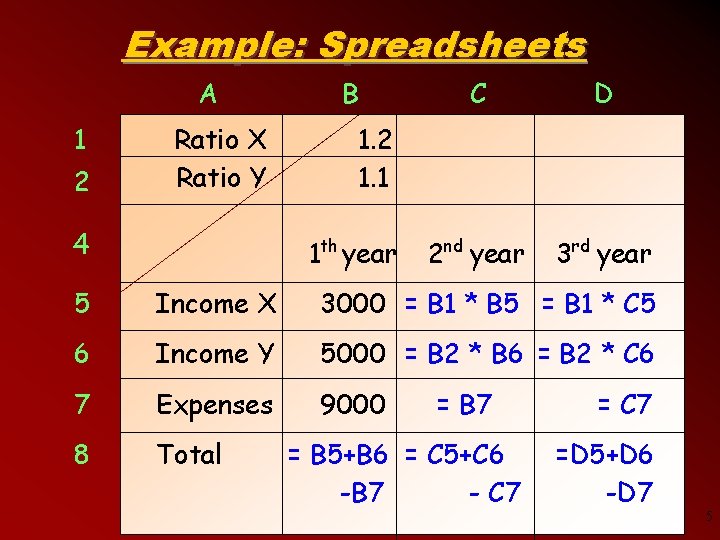
Example: Spreadsheets A 1 2 Ratio X Ratio Y 4 B C D 2 nd year 3 rd year 1. 2 1. 1 1 th year 5 Income X 3000 = B 1 * B 5 = B 1 * C 5 6 Income Y 5000 = B 2 * B 6 = B 2 * C 6 7 Expenses 9000 8 Total = B 7 = B 5+B 6 = C 5+C 6 - C 7 -B 7 = C 7 =D 5+D 6 -D 7 5

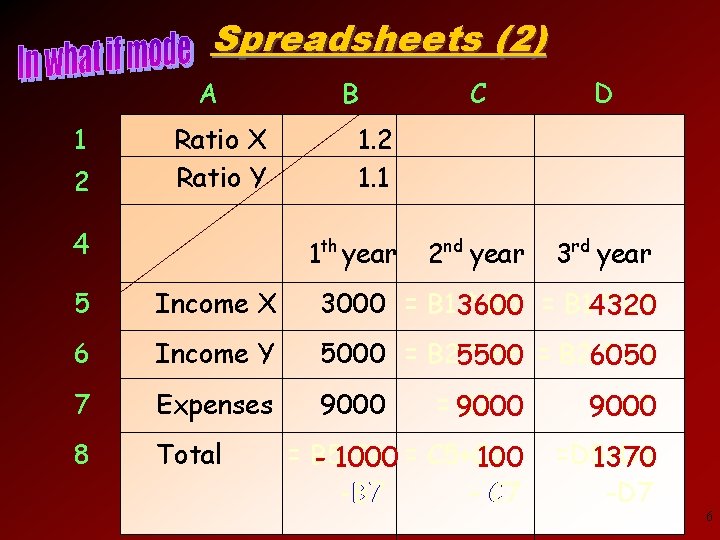
Spreadsheets (2) A 1 2 Ratio X Ratio Y 4 B C D 2 nd year 3 rd year 1. 2 1. 1 1 th year 5 Income X 3000 = B 13600 * B 5 = B 14320 * C 5 6 Income Y 5000 = B 25500 * C 6 * B 6 = B 26050 7 Expenses 9000 8 Total = 9000 B 7 = C 7 9000 = B 5+B 6 - 1000 = C 5+C 6 100 - C 7 -B 7 =D 5+D 6 1370 -D 7 6

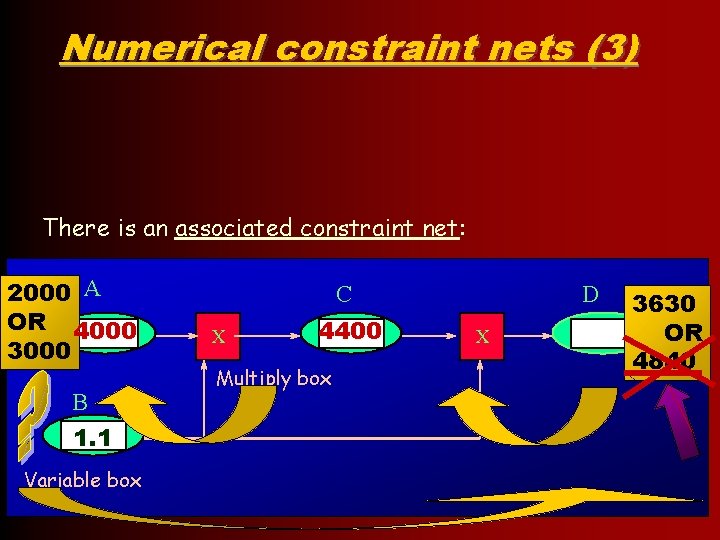
Numerical constraint nets (3) There is an associated constraint net: 2000 A OR 4000 3000 B 1. 1 Variable box C X 4400 Multiply box D X 3630 OR 4840

Defining Constraint problems Definition File rouge

Defining Constraint problems ¤ Definition: A constraint problem (or consistent labeling problem) consists of: è a finite set of variables: z 1, z 2, … , zn è for each variable: an associated finite domain of possible values di = {ai 1, ai 2, … , aini} è for each two variables zi, zj, i j, a constraint c(zi, zj) u ex. : zi zj zi + i zj - j u we restrict ourselves to binary CPS ¤ Problem: build efficient techniques to assign to each zi a value aij from its domain di such that all c(zi, zj) are true. 9

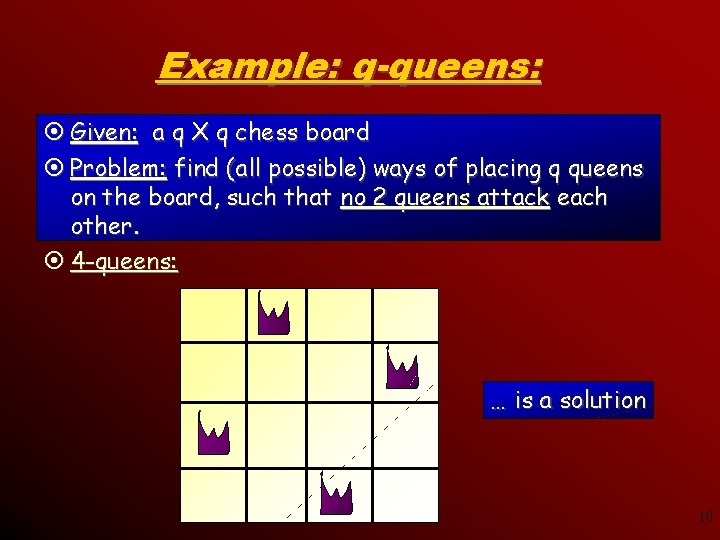
Example: q-queens: ¤ Given: a q X q chess board ¤ Problem: find (all possible) ways of placing q queens on the board, such that no 2 queens attack each other. ¤ 4 -queens: … is a solution 10

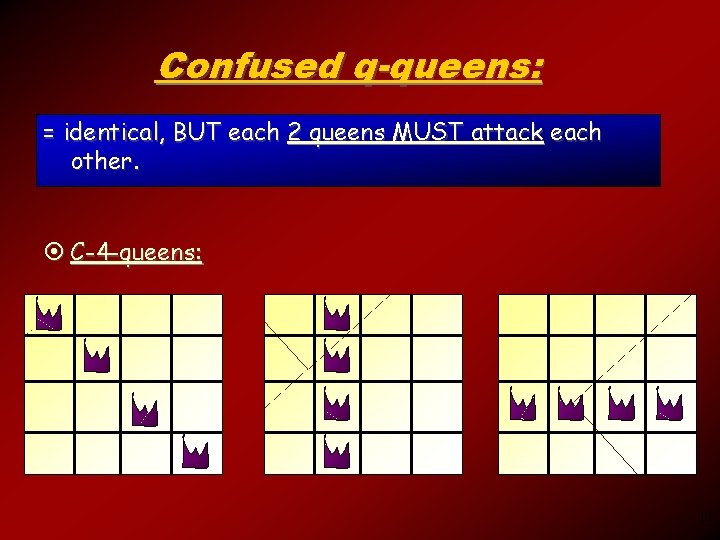
Confused q-queens: = identical, BUT each 2 queens MUST attack each other. ¤ C-4 -queens: 11

Constraint formulation? ¤ Q-queens and C-q-queens define a set of constraint problems: è depends on choice of domains, constraints ¤ One possibility: è for each queen: a variable zi è for each zi, domain di is all possible board positions: u di = { (1, 1), (1, 2), …, (1, q), (2, 1), (2, 2), … } è c(zi, zj) = row(zi) row(zj) col(zi) col(zj) |row(zi) - row(zj)| |col(zi) - col(zj)| 12

A ‘better’ formulation: ¤ We agree that each queen is placed on a specific row: 1 2 3 4 z 1 z 2 z 3 z 4 ¤ The representation: è for queen on row i: a variable zi è for each zi, domain di = { 1, 2, … , q} è c(zi, zj) = zi zj |zi - zj| |i - j| 13

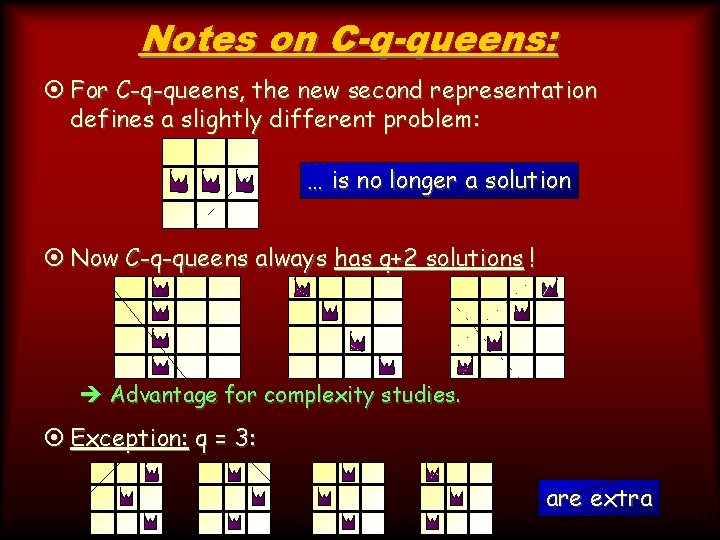
Notes on C-q-queens: ¤ For C-q-queens, the new second representation defines a slightly different problem: … is no longer a solution ¤ Now C-q-queens always has q+2 solutions ! è Advantage for complexity studies. ¤ Exception: q = 3: are extra 14

Representing the search Or-tree representation Constraint Networks

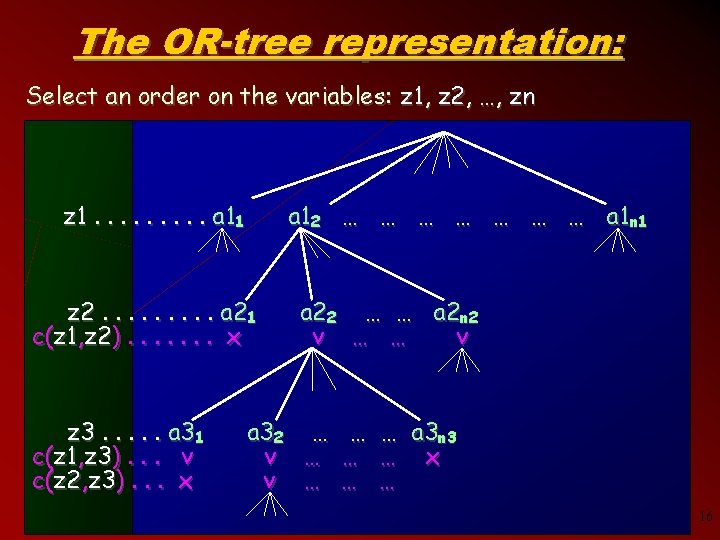
The OR-tree representation: Select an order on the variables: z 1, z 2, …, zn z 1. . a 11 a 12 … … … … a 1 n 1 z 2. . a 21 c(z 1, z 2). . . . x z 3. . . a 31 c(z 1, z 3). . . v c(z 2, z 3). . . x a 22 … … a 2 n 2 v … … v a 32 … … … a 3 n 3 v … … … x v … … … 16

OR-tree: explicitly ¤ For each layer (i) in the OR-tree: è Create a branch for every possible assignment to zi è Verify all constraints c(zj, zi), j i è If all constraints are satisfied, proceed to level i+1 ¤ NOTE: this is only a representation for the search è search itself consists of building a (small) part of this tree (as in search techniques) 17

Constraint Networks {a 11, a 12, …, a 1 n 1} z 1 c(z 1, z 2) c(z 1, z 4) {a 21, a 22, …, a 2 n 2} c(z 1, z 3) {a 41, a 42, …, a 4 n 4} z 2 z 4 c(z 2, z 4) c(z 2, z 3) c(z 3, z 4) z 3 {a 31, a 32, …, a 3 n 3} + relaxation = select an arc (constraint) and remove the inconsistent domain values 18

Relaxation: c(a 1 i, a 41) is never true! {a 11, a 12, …, a 1 n 1} z 1 c(z 1, z 2) c( c(z 1 z 1, , z 4)) {a 21, a 22, …, a 2 n 2} c(z 1, z 3) {a 4 a 411, a 42, …, a 4 n 4} z 2 z 4 c(z 2, z 4) c(z 2, z 3) c(z 3, z 4) z 3 {a 31, a 32, …, a 3 n 3} 19

Backtrack algorithms Chronological Backtracking Backjumping Backmarking Intelligent Backtracking Dynamic Search Rearrangement

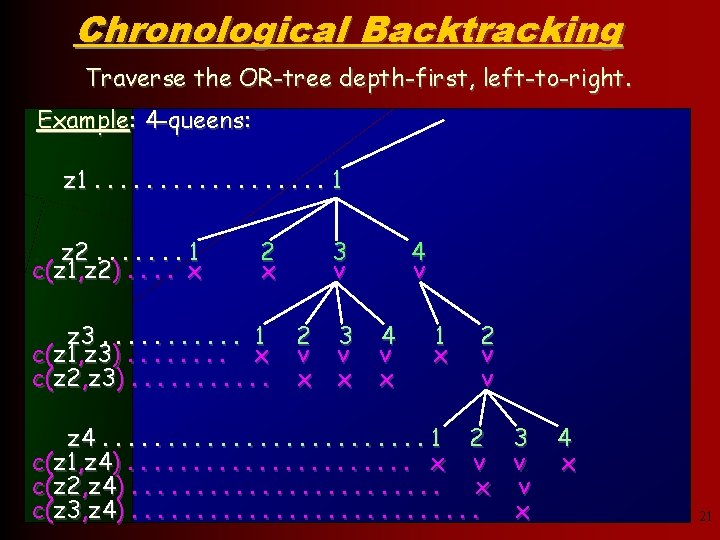
Chronological Backtracking Traverse the OR-tree depth-first, left-to-right. Example: 4 -queens: z 1. . . . 1 z 2. . . . 1 c(z 1, z 2). . x 2 x z 3. . . 1 c(z 1, z 3). . . . x c(z 2, z 3). . . 3 v 2 v x 3 v x 4 v x 1 x 2 v v z 4. . . 1 2 3 c(z 1, z 4). . . . . x v v c(z 2, z 4). . . x v c(z 3, z 4). . . . x 4 x 21

The backtrack algorithm: Backtr( depth ) For k= 1 to ndepth do zdepth. . adepth, k zdepth : = adepth, k ; c(z 1 z 1, , zzdepth v c(z 1, z c( depth)). . . v Check all constraints c(zi, zdepth) c( c(z 2 z 2, , zzdepth v c(z 2, z depth)). . . x with 1 i depth until one fails; c(zdepth-1, zdepth) v If none failed then zdepth+1. . adepth+1, 1 If depth = n then return( z 1, z 2, … , zn) Else depth : = depth + 1; Backtr( depth ) ; depth : = depth - 1; End-For Call : Backtr( 1 ) 22

Backjumping Avoid trashing

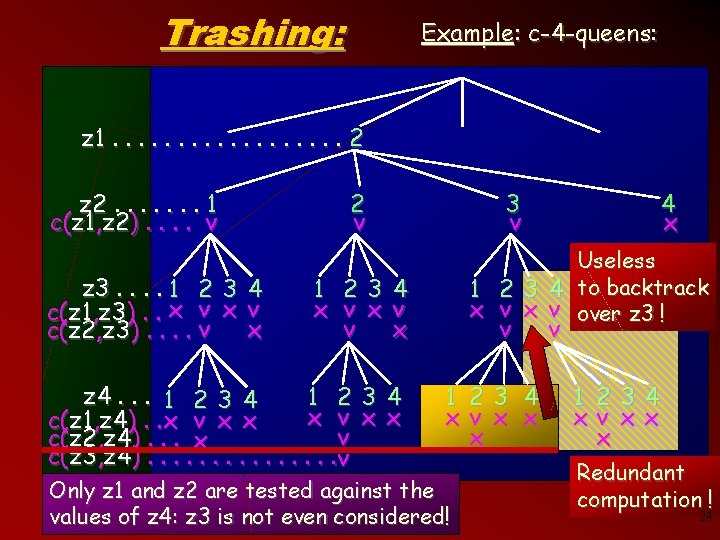
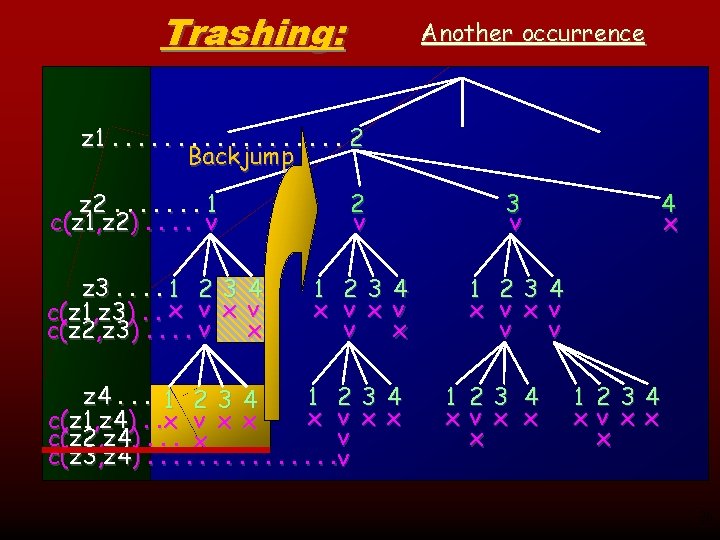
Trashing: Example: c-4 -queens: z 1. . . . 2 z 2. . . . 1 c(z 1, z 2). . v z 3. . 1 2 3 4 c(z 1, z 3). . x v x c(z 2, z 3). . v 2 v 3 v Useless 1 2 3 4 to backtrack x v over z 3 ! 1 23 4 x v v x z 4. . . 1 2 3 4 1 23 4 x v x x c(z 1, z 4). . x v x x v c(z 2, z 4). . . x c(z 3, z 4). . . . v 4 x v 1 23 4 x v x x x Only z 1 and z 2 are tested against the values of z 4: z 3 is not even considered! v 1 234 xv x x x Redundant computation ! 24

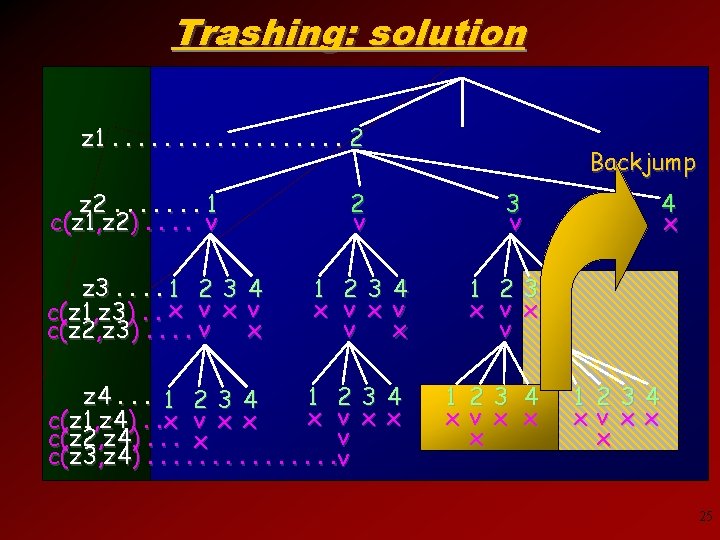
Trashing: solution z 1. . . . 2 z 2. . . . 1 c(z 1, z 2). . v z 3. . 1 2 3 4 c(z 1, z 3). . x v x c(z 2, z 3). . v Backjump 2 v 3 v 1 23 4 x v v x 1 23 4 x v v v z 4. . . 1 2 3 4 1 23 4 x v x x c(z 1, z 4). . x v x x v c(z 2, z 4). . . x c(z 3, z 4). . . . v 1 23 4 x v x x x 4 x 1 234 xv x x x 25

Trashing: Another occurrence z 1. . . . 2 Backjump z 2. . . . 1 c(z 1, z 2). . v z 3. . 1 2 3 4 c(z 1, z 3). . x v x c(z 2, z 3). . v 2 v 3 v 1 23 4 x v v x 1 23 4 x v v v z 4. . . 1 2 3 4 1 23 4 x v x x c(z 1, z 4). . x v x x v c(z 2, z 4). . . x c(z 3, z 4). . . . v 1 23 4 x v x x x 4 x 1 234 xv x x x 26

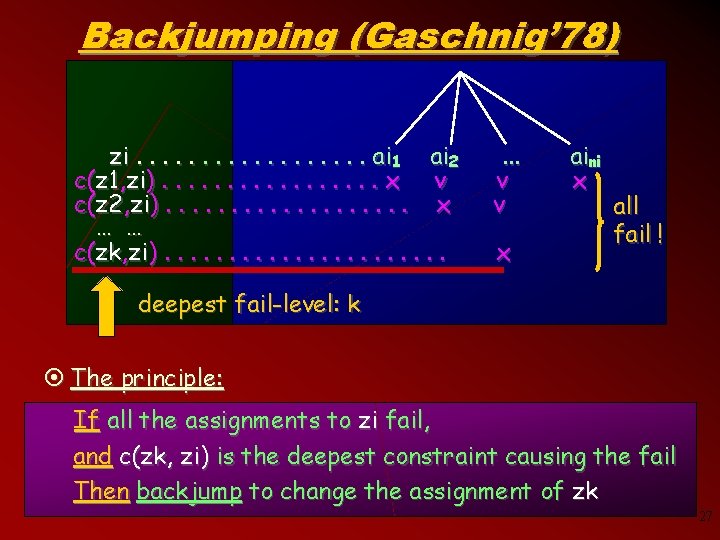
Backjumping (Gaschnig’ 78) zi. . . . ai 1 ai 2 c(z 1, zi). . . . x v c(z 2, zi). . . . . x … … c(zk, zi). . . v v x aini x all fail ! deepest fail-level: k ¤ The principle: If all the assignments to zi fail, and c(zk, zi) is the deepest constraint causing the fail Then backjump to change the assignment of zk 27

The backjump algorithm: Back. J( depth, out: jumpback ) For k= 1 to ndepth do zdepth : = adepth, k ; zdepth. . adepth, l, k Check all constraints c(zi, zdepth) zdepth c(c( z 1 z 1 , z, depth ). ). . . v v with 1 i depth until one fails; c(c( z 2 z 2 , z, depth zdepth ). ). . x. v checkdepthk : = deepest i checked; c(zm, zdepth). . . x checkdepthk = 2 If none failed then checkdepthl = m If depth = n then return( z 1, z 2, … , zn) Else depth : = depth + 1; Back. J( depth, jumpback); depth : = depth - 1; If jumpback depth then return; End-For jumpback : = max(checkdepthk) 28

Backmarking Avoiding other redundancies

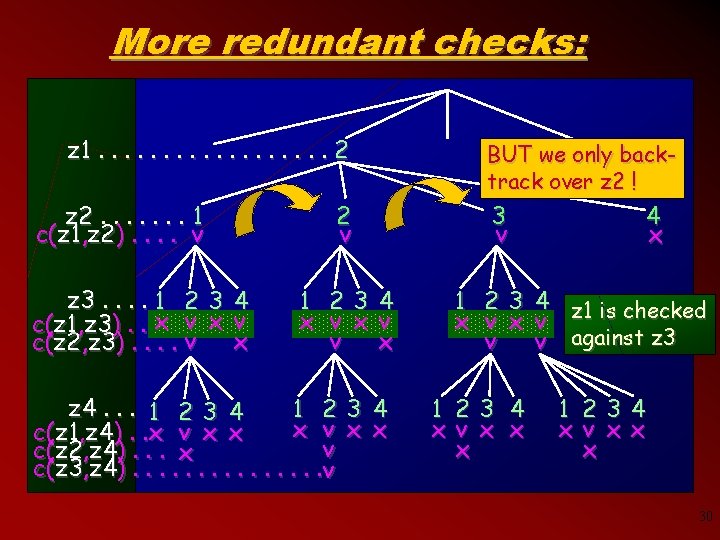
More redundant checks: z 1. . . . 2 z 2. . . . 1 c(z 1, z 2). . v z 3. . 1 2 3 4 c(z 1, z 3). . x v x c(z 2, z 3). . v 2 v 1 23 4 x v v x z 4. . . 1 2 3 4 1 23 4 x v x x c(z 1, z 4). . x v x x v c(z 2, z 4). . . x c(z 3, z 4). . . . v BUT we only backtrack over z 2 ! 3 v 4 x 1 2 3 4 z 1 is checked x v v v against z 3 1 23 4 x v x x x 1 234 xv x x x 30

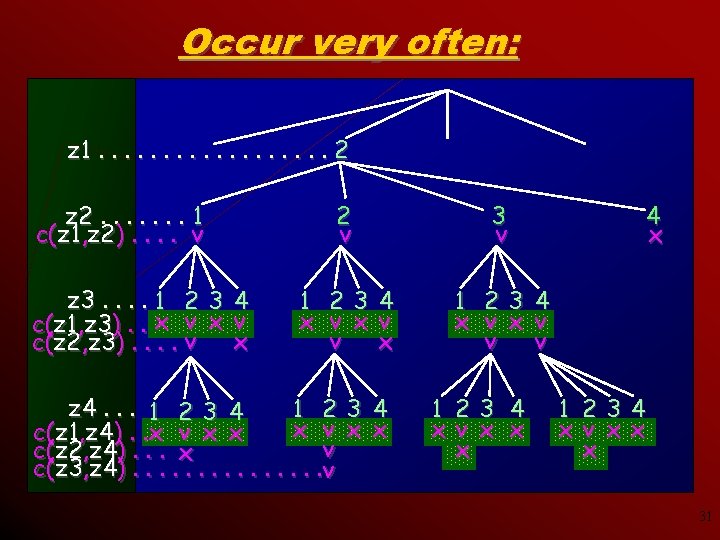
Occur very often: z 1. . . . 2 z 2. . . . 1 c(z 1, z 2). . v z 3. . 1 2 3 4 c(z 1, z 3). . x v x c(z 2, z 3). . v 2 v 3 v 1 23 4 x v v x 1 23 4 x v v v z 4. . . 1 2 3 4 1 23 4 x v x x c(z 1, z 4). . x v x x v c(z 2, z 4). . . x c(z 3, z 4). . . . v 1 23 4 x v x x x 4 x 1 234 xv x x x 31

Trashing compared to Redundant Checks: ¤ Trashing: Only when a complete BLOCK of checks FAILS. z 4. . . 1 c(z 1, z 4). . x c(z 2, z 4). . . c(z 3, z 4) 2 v x 3 x 4 x ¤ Redundant Checks: Also for SUCCESSFUL checks and for the checks performed on 1 ROW only. z 3. . 1 2 c(z 1, z 3). . x v c(z 2, z 3). . v 3 x 4 v x 1 x 2 v v 3 x 4 v x 32

Avoiding redundant checks: ¤ 2 approaches: 1. TABULATION: è lemma generation (store results of checks in a table) + lemma application (table look-up for new checks) ¤ improves speed to some extent è but does not really avoid the redundant checks ¤ increases the storage requirements 2. BACKMARKING: ¤ ~ TOTALLY speed saving (no redundant checks) ¤ only limited space-overhead (2 arrays) 33

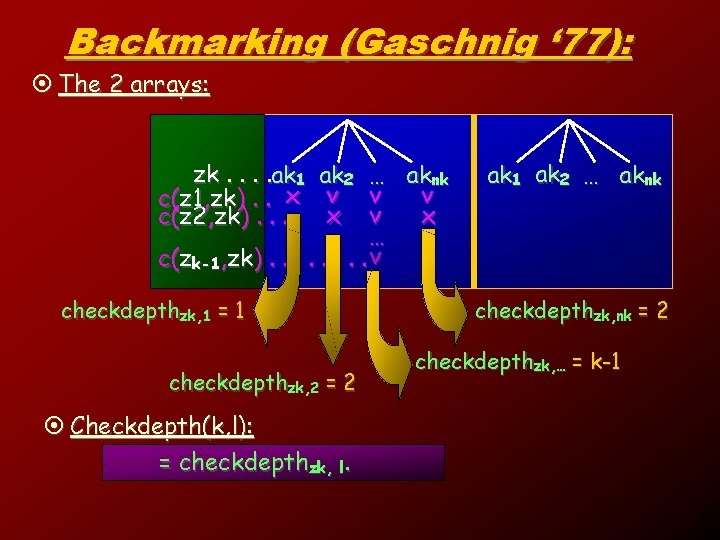
Backmarking (Gaschnig ‘ 77): ¤ The 2 arrays: zk. . ak 1 c(z 1, zk). . x c(z 2, zk). . ak 2 v x … aknk v v v x … c(zk-1, zk). . . . v checkdepthzk, 1 = 1 checkdepthzk, 2 = 2 ak 1 ak 2 … aknk checkdepthzk, nk = 2 checkdepthzk, … = k-1 ¤ Checkdepth(k, l): = checkdepthzk, l. 34

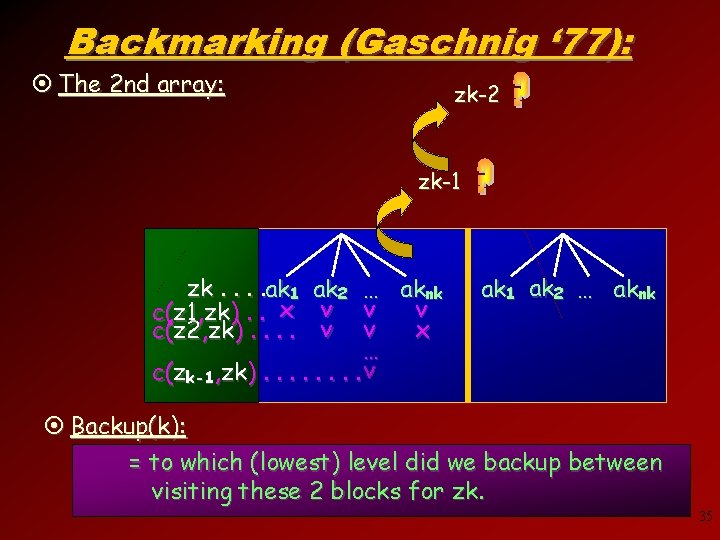
Backmarking (Gaschnig ‘ 77): ¤ The 2 nd array: zk-2 zk-1 zk. . ak 1 ak 2 … aknk v c(z 1, zk). . x v v x c(z 2, zk). . v v … c(zk-1, zk). . . . v ak 1 ak 2 … aknk ¤ Backup(k): = to which (lowest) level did we backup between visiting these 2 blocks for zk. 35

A property of Checkdepthk, l ¤ If Checkdepth k, l k-1: zk. . ak, l c(z 1, zk). . v c(z 2, zk). . v … c(zi, zk). . . x The last check needs to be a FAIL. Otherwise, checking would have continued ! ¤ If Checkdepth k, l = k-1: zk. . ak, l c(z 1, zk). . v c(z 2, zk). . v … c(zk-1, zk). x/v The last check can be either fail or succeed. 36

Properties of Checkdepth versus Backup (1): ¤ If checkdepth (k, l) backup(k) : checkdepth(k, l) k-1 zk. . . . ak, l c(z 1, zk). . . v c(z 2, zk). . . v … c(zi, zk). . . x checkdepth(k, l) … backup(k) c(zk-1, zk) The assignment ak, l to zk caused fail the previous time, and it will cause fail again this time (at the same depth) 37

Properties of Checkdepth versus Backup (2): ¤ If checkdepth (k, l) backup(k) : zk. . . . ak, l c(z 1, zk). . . v c(z 2, zk). . . v … backup(k) c(zi, zk). . . v … c(zj, zk). . v/x checkdepth(k, l) All checks for variables zm, with m lower than backup(k) succeeded before and will succeed again. 38

The Backmark algorithm: Back. M( depth, out: checkdepth, backup ) For k= 1 to ndepth do zdepth : = adepth, k ; If checkdepth(depth, k) backup(depth) Then *property 1 applied* Check all constraints c(zi, zdepth) with backup(depth 1)1 i depth until one fails; *property 2 applied* If none failed then ……… End-For 39

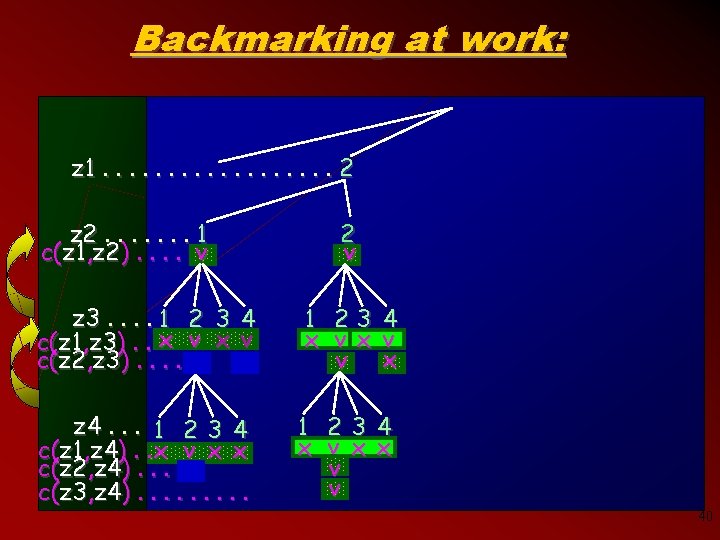
Backmarking at work: z 1. . . . 2 z 2. . . . 1 c(z 1, z 2). . v z 3. . 1 2 c(z 1, z 3). . x v c(z 2, z 3). . v 2 v 3 x 4 v x 1 x 23 v x v 4 v x z 4. . . 1 2 3 4 c(z 1, z 4). . x v x x c(z 2, z 4). . . x c(z 3, z 4). . 1 x 2 v v v 4 x 3 x 40

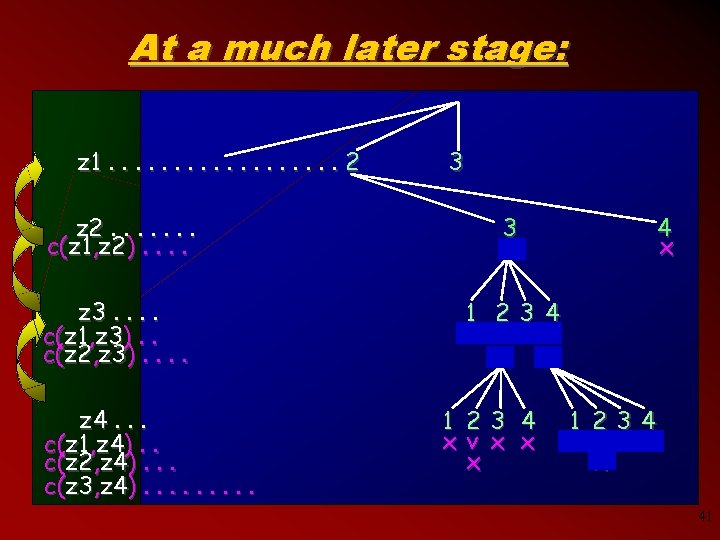
At a much later stage: z 1. . . . 2 3 z 2. . . . c(z 1, z 2). . 3 v z 3. . c(z 1, z 3). . c(z 2, z 3). . 1 23 4 x v v v z 4. . . c(z 1, z 4). . c(z 2, z 4). . . c(z 3, z 4). . 1 23 4 x v x x x 4 x 1 234 xv x x x 41

Discussion and results: Note: initial values for checkdepth(k, l) and backup(k) are all 1 ¤ Experimental results: è For c-4 -queens problem BT BJ BM Nodes 29 27 29 Checks 160 139 90 ¤ Overall: è Back. Marking = best algorithm (not absolute) ¤ Combining BJ and BM? YES ! è But does not produce the combined optimisation. 42

Dynamic Search rearrangement

Dynamic search rearrangement ¤ = any backtrack algorithm + select the order of the variables in the tree dynamically ¤ Purpose: Decrease the size of the tree due to the “first-fail principle” ¤ The first-fail principle: If assigning a value to zi is more likely to fail than assigning to zj: Then: assing to zi first. 44

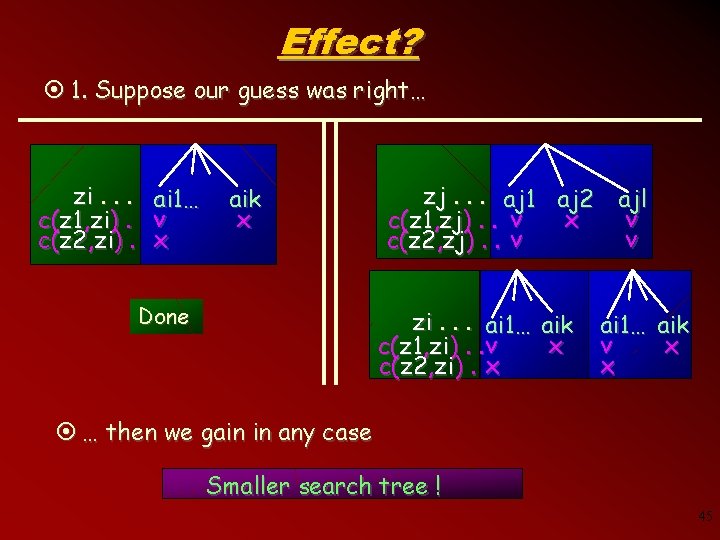
Effect? ¤ 1. Suppose our guess was right… zi. . . ai 1… c(z 1, zi). . v c(z 2, zi). . xx aik x Done zj. . . aj 1 aj 2 ajl x v c(z 1, zj). . v v c(z 2, zj). . v zi. . . ai 1… aik x c(z 1, zi). . v c(z 2, zi). x ai 1… aik v x x ¤ … then we gain in any case Smaller search tree ! 45

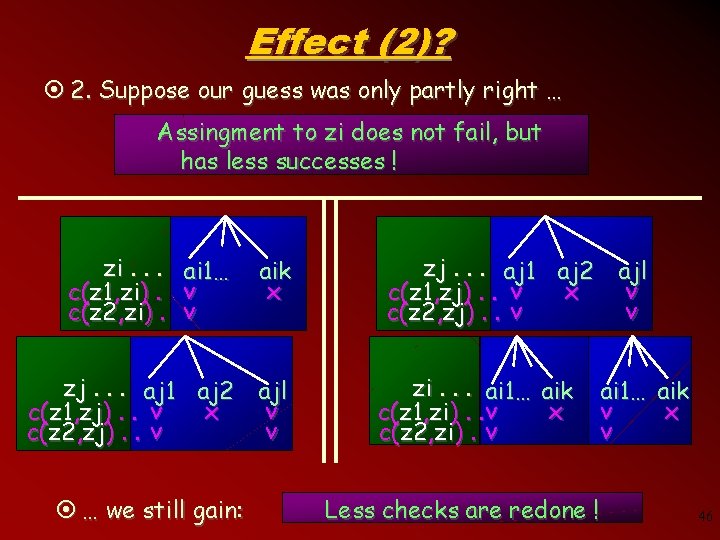
Effect (2)? ¤ 2. Suppose our guess was only partly right … Assingment to zi does not fail, but has less successes ! zi. . . ai 1… c(z 1, zi). . v c(z 2, zi). . vx aik x zj. . . aj 1 aj 2 ajl x v c(z 1, zj). . v v c(z 2, zj). . v ¤ … we still gain: zj. . . aj 1 aj 2 ajl x v c(z 1, zj). . v v c(z 2, zj). . v zi. . . ai 1… c(z 1, zi). . v c(z 2, zi). v aik x ai 1… v v Less checks are redone ! aik x 46

Some general first-fail heuristics: è Select the variable with the smallest domain first decreases the branching factor (less possibilities -> probably less successes) è Select the variable with the highest number of nontrivial constraints first: c(z 1, z 2) z 2 “true” = c(z 2, z 3) z 1 c(z 1, z 3) z 3 c(z 1, z 4) = “true” z 4 c(z 2, z 4) c(z 3, z 4) = “true” + Heuristics based on problem at hand. 47