Finite Constraint Domains 1 Finite Constraint Domains Constraint









































![Bounds Consistency arithmetic CSP: domains = integers u range: [l. . u] represents the Bounds Consistency arithmetic CSP: domains = integers u range: [l. . u] represents the](https://slidetodoc.com/presentation_image_h/782f24a12cfc923f1b7cf42b9a497ce0/image-48.jpg)





























- Slides: 77

Finite Constraint Domains 1

Finite Constraint Domains Constraint satisfaction problems (CSP) u A backtracking solver u Node and arc consistency u Bounds consistency u Generalized consistency u Optimization for arithmetic CSPs u 2

Finite Constraint Domains An important class of constraint domains u Use to model constraint problems involving choice: e. G. Scheduling, routing and timetabling u The greatest industrial impact of constraint programming has been on these problems u 3

Constraint Satisfaction Problems u A constraint satisfaction problem (CSP) consists of: u. A constraint C over variables x 1, . . . , Xn u A domain D which maps each variable xi to a set of possible values d(xi) u It is understood as the constraint 4

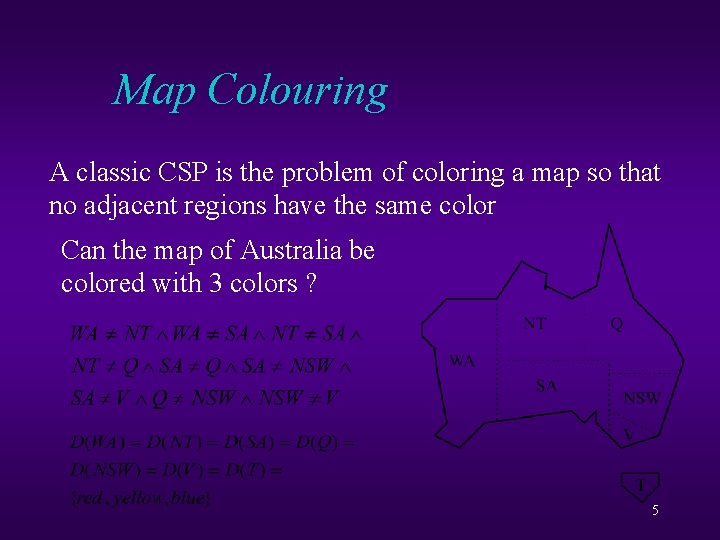
Map Colouring A classic CSP is the problem of coloring a map so that no adjacent regions have the same color Can the map of Australia be colored with 3 colors ? 5

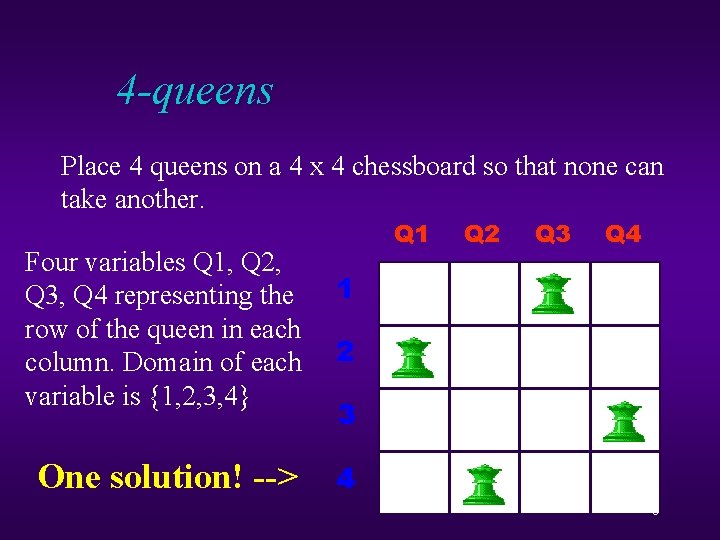
4 -queens Place 4 queens on a 4 x 4 chessboard so that none can take another. Four variables Q 1, Q 2, Q 3, Q 4 representing the row of the queen in each column. Domain of each variable is {1, 2, 3, 4} One solution! --> Q 1 Q 2 Q 3 Q 4 1 2 3 4 6

4 -queens The constraints: Not on the same row Not diagonally up Not diagonally down 7

Smugglers Knapsack Smuggler with knapsack with capacity 9, who needs to choose items to smuggle to make profit at least 30 What should be the domains of the variables? 8

Systematic Search Methods u exploring the solution space u complete and sound u efficiency issues exploring subspace u Backtracking (BT) u Generate & Test (GT) exploring individual assignments Z X 9 Y

Generate & Test probably the most general problem solving method u Algorithm: u generate labelling test satisfaction Drawbacks: blind generator late discovery of inconsistencies Improvements: smart generator --> local search testing within generator --> backtracking 10

Backtracking (BT) u u u incrementally extends a partial solution towards a complete solution Algorithm: A 1 assign value to variable B 2 check consistency 1 until all variables labelled C 2 1 1 Drawbacks: D u thrashing 1 1 2 u redundant work A = D, B D, A+C < 4 u late detection of conflict 11

GT & BT - Example u Problem: X: : {1, 2}, Y: : {1, 2}, Z: : {1, 2} X = Y, X Z, Y > Z generate & test backtracking 12

Simple Backtracking Solver The simplest way to solve CSPs is to enumerate the possible solutions u The backtracking solver: u u Enumerates values for one variable at a time u Checks that no prim. Constraint is false at each stage u Assume satisfiable(c) returns false when primitive constraint c with no variables is unsatisfiable 13

Partial Satisfiable Check whether a constraint is unsatisfiable because of a prim. Constraint with no vars u Partial_satisfiable(c) Partial_satisfiable u u For each primitive constraint c in C u If vars(c) is empty u If satisfiable(c) = false return false u Return true 14

Backtrack Solve u Back_solve(c, d) Back_solve u If vars(c) is empty return partial_satisfiable(c) partial_satisfiable u Choose x in vars(c) u For each value d in d(x) u Let C 1 be C with x replaced by d u If partial_satisfiable(c 1) partial_satisfiable( then u If back_solve(c 1, d) then return true back_solve u Return false 15

Backtracking Solve Choose Variablevar XZ X Y Choose var Y domain {1, 2} partial_satisfiable No variables, false and false No variables, and false 16

Consistency Techniques u u u removing inconsistent values from variables’ domains graph representation of the CSP u binary and unary constraints only (no problem!) A>5 u nodes = variables A u edges = constraints A<C A B node consistency (NC) arc consistency (AC) C path consistency (PC) B B=C (strong) k-consistency 17

Node and Arc Consistency Basic idea: find an equivalent CSP to the original one with smaller domains of vars u Key: examine 1 prim. Constraint c at a time u Node consistency: (vars(c)={x}) remove any values from domain of x that falsify c u Arc consistency: (vars(c)={x, y}) remove any values from d(x) for which there is no value in d(y) that satisfies c and vice versa u 18

Node Consistency u Primitive constraint c is node consistent with domain D if |vars(c)| /=1 or u If vars(c) = {x} then for each d in d(x) u X assigned d is a solution of c u A CSP is node consistent if each prim. Constraint in it is node consistent 19

Node Consistency Examples Example CSP is not node consistent (see Z) This CSP is node consistent The map coloring and 4 -queens CSPs are node consistent. Why? 20

Achieving Node Consistency u u Node_consistent(c, d) Node_consistent u For each prim. Constraint c in C u D : = node_consistent_primitive(c, node_consistent_primitive D) u Return D Node_consistent_primitive(c, Node_consistent_primitive D) u If |vars(c)| =1 then u Let {x} = vars(c) u Return D 21

Arc Consistency u A primitive constraint c is arc consistent with domain D if |vars{c}| != 2 or u Vars(c) = {x, y} and for each d in d(x) there exists e in d(y) such that u And u similarly for y A CSP is arc consistent if each prim. Constraint in it is arc consistent 22

Arc Consistency Examples This CSP is node consistent but not arc consistent For example the value 4 for X and X < Y. The following equivalent CSP is arc consistent The map coloring and 4 -queens CSPs are also arc consistent. 23

Achieving Arc Consistency u Arc_consistent_primitive(c, Arc_consistent_primitive u If |vars(c)| = 2 then u Return u D) D Removes values which are not arc consistent 24 with c

Achieving Arc Consistency u Arc_consistent(c, d) Arc_consistent u Repeat u. W : = d u For each prim. Constraint c in C u D : = arc_consistent_primitive(c, d) arc_consistent_primitive u Until W = D u Return D u A very naive version (there are much better) 25

Using Node and Arc Cons. We can build constraint solvers using the consistency methods u Two important kinds of domain u u False domain: some variable has empty domain u Valuation domain: each variable has a singleton domain u Extend satisfiable to CSP with val. Domain 26

Node and Arc Cons. Solver D : = node_consistent(C, D) node_consistent u D : = arc_consistent(C, D) arc_consistent u if D is a false domain u u return u if D is a valuation domain u return u false satisfiable(C, D) return unknown 27

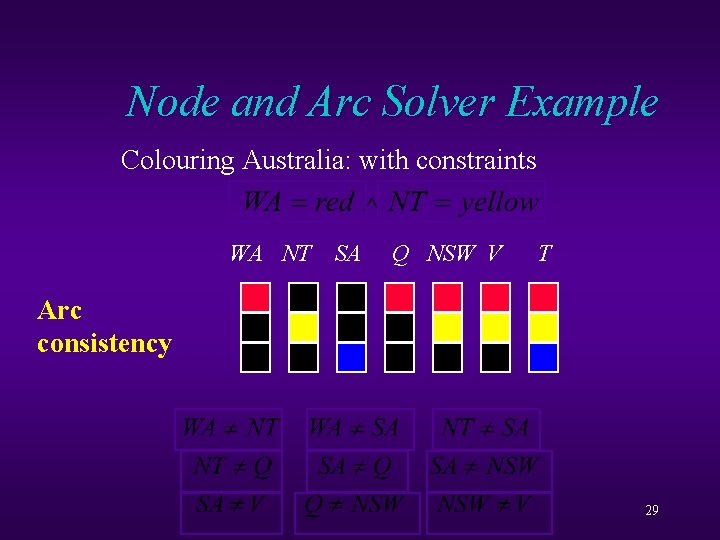
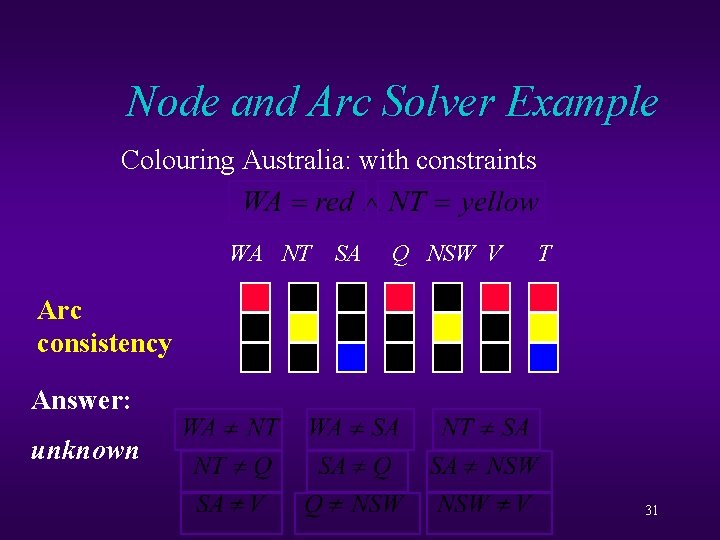
Node and Arc Solver Example Colouring Australia: with constraints WA NT SA Q NSW V T Node consistency 28

Node and Arc Solver Example Colouring Australia: with constraints WA NT SA Q NSW V T Arc consistency 29

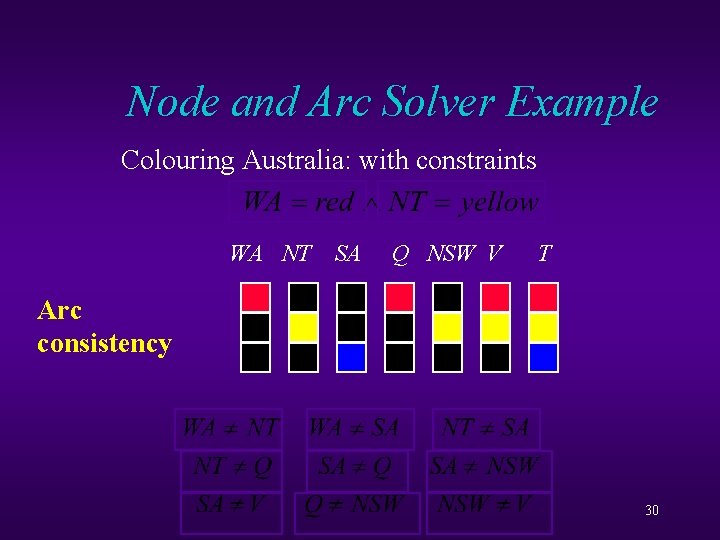
Node and Arc Solver Example Colouring Australia: with constraints WA NT SA Q NSW V T Arc consistency 30

Node and Arc Solver Example Colouring Australia: with constraints WA NT SA Q NSW V T Arc consistency Answer: unknown 31

Backtracking Cons. Solver We can combine consistency with the backtracking solver u Apply node and arc consistency before starting the backtracking solver and after each variable is given a value u 32

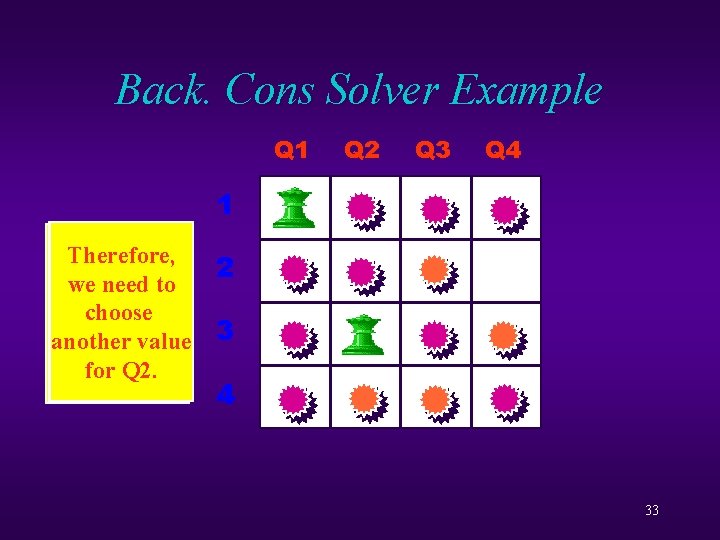
Back. Cons Solver Example Q 1 Q 2 Q 3 Q 4 1 Therefore, No value There is no wecan need be to possible choose to assigned value for another value Q 3 in this variable Q 3! for Q 2. case! 2 3 4 33

Back. Cons Solver Example Q 1 Q 2 Q 3 Q 4 1 backtracking, Backtracking… backtracking, We cannot 2 find any Find another possible value of value Q 1? value for Q 3? 3 value of Q 2? for Q 4 in No! this case! Yes, Q 1 =2 4 34

Back. Cons Solver Example Q 1 Q 2 Q 3 Q 4 1 2 3 4 35

Back. Cons Solver Example Q 1 Q 2 Q 3 Q 4 1 2 3 4 36

Node and Arc Solver Example Colouring Australia: with constraints WA NT SA Q NSW V T Backtracking enumeration Select a variable with domain of more than 1, T Add constraint Answer: true Apply consistency 37

Is AC enough? u u u empty domain => no solution cardinality of all domains is 1 => solution X Problem: 1 X: : {1, 2}, Y: : {1, 2}, Z: : {1, 2} X Y, X Z, Y Z Y 1 2 2 1 2 38 Z

Path Consistency (PC) V 2 V 0 V 3 V 1 V 4 V 5 ? ? ? u Path (V 0 … Vn) is path consistent iff for each pair of compatible values x in D(V 0) and y in D(Vn) there exists an instantiation of the variables V 1. . Vn-1 such that all the constraint (Vi, Vi+1) are satisfied CSP is path consistent iff each path is path consistent u consistency along the path only u 39

Path Consistency (PC) V 2 V 0 V 3 V 1 V 4 V 5 ? ? ? checking paths of length 2 is enough u Plus/Minus u + detects more inconsistencies than AC - extensional representation of constraints (01 matrix), huge memory consumption - changes in graph connectivity 40

K -consistency u K-consistency u consistent valuation o (K-1) variables can be extended to K-th variable u strong K-consistency J-consistency for each J K 41

Is k-consistency enough ? u u u If all the domains have cardinality 1=> solution If any domain is empty => no solution Otherwise ? strongly k-consistent constraint graph with k nodes => completeness for some special kind of graphs weaker forms of consistency are enough 42

Consistency Completeness u u strongly N-consistent constraint graph with N nodes => solution strongly K-consistent constraint graph with N nodes (K<N) => ? ? ? A D {1, 2, 3} path consistent but no solution u {1, 2, 3} B C {1, 2, 3} Special graph structures u tree structured graph => (D)AC is enough 43

hyper-arc consistency u A primitive constraint c is hyper-arc consistent with domain D if u for each variable x in c and for each d in d(x) the valuation x-->d can be extended to a solution of c u A CSP is hyper-arc consistent if each prim. Constraint in it is hyper-arc consistent u u NC hyper-arc consistency for constraint with 1 var AC hyper-arc consistency for constraint with 2 var 44

Non binary constraints What about prim. constraints with more than 2 variables? u Each CSP can be transformed into an equivalent binary CSP (dual encoding) u k-consitncy u hyper-arc consistency u 45

Dual encoding u Each CSP can be transformed into an equivalent binary CSP by ``dual encoding’’: u k-ary constraint c is converted to a dual variable vc with the domain consisting of compatible tuples for each pair of constraint c, c’ sharing some variable there is a binary constraint between vc and vc’ restricting the dual variables to tuples in which the original shared variables take the same value u 46

Hyper-arc consistency hyper-arc consistency: extending arc consistency to arbitrary number of variables u (better than binary representation) u Unfortunately determining hyper-arc consistency is NP-hard (as expensive as determinining if a CSP is satisfiable). u Solution? u 47
![Bounds Consistency arithmetic CSP domains integers u range l u represents the Bounds Consistency arithmetic CSP: domains = integers u range: [l. . u] represents the](https://slidetodoc.com/presentation_image_h/782f24a12cfc923f1b7cf42b9a497ce0/image-48.jpg)
Bounds Consistency arithmetic CSP: domains = integers u range: [l. . u] represents the set of integers {l, l+1, . . . , u} u idea use real number consistency and only examine the endpoints (upper and lower bounds) of the domain of each variable u Define min(D, x) as minimum element in domain of x, similarly for max(D, x) u 48

Bounds Consistency u A prim. constraint c is bounds consistent with domain D if for each var x in vars(c) u exist real numbers d 1, . . . , dk for remaining vars x 1, . . . , xk such that min(D, xj), = dj<= max(D, xj) and is a solution of c u and similarly for u An arithmetic CSP is bounds consistent if all its primitive constraints are 49

Bounds Consistency Examples Not bounds consistent, consider Z=2, then X-3 Y=10 But the domain below is bounds consistent Compare with the hyper-arc consistent domain 50

Achieving Bounds Consistency Given a current domain D we wish to modify the endpoints of domains so the result is bounds consistent u propagation rules do this u 51

Achieving Bounds Consistency Consider the primitive constraint X = Y + Z which is equivalent to the three forms Reasoning about minimum and maximum values: Propagation rules for the constraint X = Y + Z 52

Achieving Bounds Consistency The propagation rules determine that: Hence the domains can be reduced to 53

More propagation rules Given initial domain: We determine that new domain: 54

Disequations give weak propagation rules, only when one side takes a fixed value that equals the minimum or maximum of the other is there propagation 55

Multiplication If all variables are positive its simple enough Example: becomes: But what if variables can be 0 or negative? 56

Multiplication Calculate X bounds by examining extreme values Similarly for upper bound on X using maximum BUT this does not work for Y and Z? As long as min(D, Z) <0 and max(D, Z)>0 there is no bounds restriction on Y Recall we are using real numbers (e. g. 4/d) 57

Multiplication We can wait until the range of Z is non-negative or non-positive and then use rules like division by 0: 58

Bounds Consistency Algm Repeatedly apply the propagation rules for each primitive constraint until there is no change in the domain u We do not need to examine a primitive constraint until the domains of the variables involve are modified u 59

Bounds Consistency Example Smugglers knapsack problem (no whiskey available) Continuing there is no further change Note how we had to reexamine the profit constraint 60

Bounds consistency solver D : = bounds_consistent(C, D) bounds_consistent u if D is a false domain u u return u if D is a valuation domain u return u false satisfiable(C, D) return unknown 61

Back. Bounds Cons. Solver u Apply bounds consistency before starting the backtracking solver and after each variable is given a value 62

Back. Bounds Solver Example Smugglers knapsack problem (whiskey available) Current domain: Initial bounds consistency W=0 P=1 (0, 1, 3) Solution Found: return true 63

Back. Bounds Solver Example Smugglers knapsack problem (whiskey available) Current domain: Backtrack Initial bounds consistency W=0 P=1 P=2 P=3 (0, 1, 3) false (0, 3, 0) W=1 W=2 (1, 1, 1) (2, 0, 0) No more solutions 64

Generalized Consistency u Can use any consistency method with any other communicating through the domain, u node consistency : prim constraints with 1 var u arc consistency: prim constraints with 2 vars u bounds consistency: other prim. constraints u Sometimes we can get more information by using complex constraints and special consistency methods 65

Alldifferent u alldifferent({V 1, . . . , Vn}) holds when each variable V 1, . . , Vn takes a different value u alldifferent({X, Y, Z}) is equivalent to u Arc consistent with domain u BUT there is no solution! specialized consistency for alldifferent can find it 66

Alldifferent Consistency let c be of the form alldifferent(V) u while exists v in V where D(v) = {d} u u. V : = V - {v} u for each v’ in V u D(v’) : = D(v’) - {d} DV : = union of all D(v) for v in V u if |DV| < |V| then return false domain u return D u 67

Alldifferent Examples DV = {1, 2}, V={X, Y, Z} hence detect unsatisfiability DV = {1, 2, 3, 4, 5}, V={X, Y, Z, T} don’t detect unsat. Maximal matching based consistency could 68

Other Complex Constraints u schedule n tasks with start times Si and durations Di needing resources Ri where L resources are available at each moment u array access if I = i, then X = Vi and if X != Vi then I != i 69

Optimization for CSPs Because domains are finite can use a solver to build a straightforward optimizer u retry_int_opt(C, retry_int_opt D, f, best) u u D 2 : = int_solv(C, D) int_solv u if D 2 is a false domain then return best u let sol be the solution corresponding to D 2 u return retry_int_opt(C retry_int_opt / f < sol(f), D, f, sol) 70

Retry Optimization Example Smugglers knapsack problem (optimize profit) First Next No next solution! found: Corresponding Return best solution 71

Backtracking Optimization Since the solver may use backtrack search anyway combine it with the optimization u At each step in backtracking search, if best is the best solution so far add the constraint f < best(f) u 72

Back. Optimization Example Smugglers knapsack problem (whiskey available) Current domain: Initial bounds consistency W=0 P=1 (0, 1, 3) Solution Found: add constraint 73

Back. Optimization Example Smugglers knapsack problem (whiskey available) Initial bounds consistency W=0 P=1 P=2 P=3 (0, 1, 3) false W=1 W=2 (1, 1, 1) false 74 Modify constraint Return last sol (1, 1, 1)

Branch and Bound Opt. The previous methods, unlike simplex don't use the objective function to direct search u branch and bound optimization for (C, f) u u use simplex to find a real optimal, u if solution is integer stop u otherwise choose a var x with non-integer opt value d and examine the problems u use the current best solution to constrain prob. 75

Branch and Bound Example Smugglers knapsack problem false Solution (2, 0, 0) = 30 Solution (1, 1, 1) = 32 false Worse than best sol false 76

Finite Constraint Domains Summary CSPs form an important class of problems u Solving of CSPs is essentially based on backtracking search u Reduce the search using consistency methods u u u node, arc, bound, generalized Optimization is based on repeated solving or using a real optimizer to guide the search 77