CSC 102 INTRODUCTION TO ALGORITHM DEVELOPMENT Falana O

CSC 102: INTRODUCTION TO ALGORITHM DEVELOPMENT Falana O. J. Falana O. J. by Introduction to Algorithm Development is licensed under a Creative Commons Attribution-Non Commercial 4. 0 International License 1

Classroom Etiquette n It is important that we all be respectful of each other in class: Ø Ø n n There is to be no ridiculing of other students, under any circumstances. Any critiques during a presentation are to be directed to the presenter. Any critiques during a presentation are to be phrased as inquiries, not as accusations. The presenter is to respond politely to all questions. Do not violate these rules. As the course instructor, it will be my obligation to enforce these rules. 2

COURSE OUTLINES Module 1 n Problem Solving Strategies n What is a Problem? n PROBLEM SOLVING STAGES n Human versus Computers in Solving Problem 3

COURSE OUTLINES (Continued) n Module 2 : Problem Solving Process in Computing Ø Ø n Problem Solving Process in Computing using Algorithm Flowcharts Pseudo Codes Module 3: Roles of algorithm in problem solving process Ø Ø Roles of algorithm in problem solving process Implementation strategies, concepts and properties of algorithm 4

COURSE OUTLINES (Continued) Module 4: Introduction to C language part 1 § Definition and introduction to: ü ü § Variables Operators Expressions Statements Definition and introduction to: ü ü ü Compiler Keywords Header files n n Control Flow Constructs Decisions ü ü ü n IF statement Nested-IF statements Switch Statements Loops ü ü ü FOR- loop statements WHILE-Loop Statements DO-WHILE Loop Statements 5

COURSE OUTLINES (Continued) n n n Module 5: Introduction to C++ language part 2 Functions Introduction to Arrays Introduction to String and String Processing Introduction to searching and sorting concepts: Structures 6

PROBLEM SOLVING INTRODUCTION n Can you think of a day in your life which goes without problem solving? n In our life we are bound to solve problems. n In our day to day activity such as purchasing something from a general store and making payments, depositing fee in school, or withdrawing money from bank account. n All these activities involve some kind of problem solving 7

n n n To make it clearer, let us see some other examples. Example 1: If you are watching a news channel on your TV and you want to change it to a sports channel, you need to do something i. e. move to that channel by pressing that channel number on your remote. This is a kind of problem solving. Example 2: Some students in a class are planning to go on a picnic, they all decided to share the expenses among themselves. So calculating total expenses and the amount an individual have to give for picnic is also a kind of problem solving. 8

What is a Problem? n n n Ø Ø A problem is defined as the objective or the specific output that we want to attain; through a sequence of steps and activities and, specific input. Consider the following problem: The problem is: Baking a cake according to certain specifications, inputs available are the ingredients (such as eggs, flour, milk …etc. ), then followed by activities or procedures that should be done sequentially, taking into consideration that any mistake happens by doing any procedure before the other, results in an unsuitable and undesirable cake. 9

PROBLEM SOLVING STAGES First Problem Definition n Problem definition implies the identification of required outputs, available inputs and, arithmetic and logical operations to be executed. n Second: Performing step-by-step instructions (Algorithm) to solve a Problem n After identifying and analysing the problem, outputs and, inputs; a plan in the form of a series of successive steps is made, which is called an (Algorithm), Algorithm is defined as a group of logically arranged procedures to be executed to attain a goal or precise output, out of specific inputs 10

n n Program Design Having drawn a Flowchart/ Algorithm to solve the problem, we have to translate this flowchart/Algorithm into one of the programming languages. Fourth: Program Testing During writing of program we may unintentionally make some mistakes; e. g. writing a minus sign (-) instead of (+). We can’t detect errors unless we begin entering data to the program with previously known results; to compare the results of the current program to those of the well-known results; therefore we check the errors and debug them 11

n n Fifth: Program Documentation The documentation is beneficial when more than one person participate in writing or modifying the program 12

Human versus Computers in Solving problem n n n People either converge in their thinking to solve a problem or they diverge in their thinking to solve a problem—or they do both Convergent vs. Divergent Thinking: Each stage of the problem-solving process is associated with two fundamental cognitive operations, namely divergent thinking and convergent thinking. The divergent thinking operation involves searching for ideas and increasing one’s options through elaboration of the problem, redefinition of the problem, and by exploring, connecting, and/or combining potential ideas and solutions 13

n n In contrast, the convergent thinking operation involves evaluating ideas and narrowing or reducing one’s options through the imposition of value judgments, exploiting the information available about the ideas, and then prioritizing and selecting Exploitation vs. Exploration is about searching for new ideas both inside and outside the paradigm. whereas Exploitation is about taking advantage of an idea within the paradigm and perfecting it 14

n n Some business problems require mostly exploitation, while others require mostly exploration, but all problems require some mixture of the two. Computers solve problems using Algorithm. We’ll talk about algorithms in the next module 15

ALGORITHM n n n An algorithm is a well-defined computational procedure consisting of a set of instructions that takes some value or set of values, as input, and produces some value or set of values, as output OR An algorithm is a procedure consisting of a finite set of steps which specify a finite sequence of operations that provides the solution to a problem. In other word, an algorithm is a procedure that accepts data, manipulate them following the prescribed steps, so as to eventually fill the required unknown with the desired value(s). 16

Why study an Algorithms? n n Computer scientists learn by experience. We learn by seeing others solve problems and by solving problems by ourselves Algorithms are often quite different from one another Consider the example of sqrt. It is entirely possible that there are many different ways to implement the details to compute the square root function As we study algorithms, we can learn analysis techniques that allow us to compare and contrast solutions based solely on their own characteristics, not the characteristics of the program or computer used to implement them 17

Algorithm and Program What is the difference between an Algorithm and a Program? n Algorithm is meant in general to be performed by a human while the computer performs a program. n Algorithm is the mathematical step-by-step procedure while a Program is the implementation of the algorithm in a particular programming language n Find out more differences 18

Properties of an Algorithm Finiteness: An algorithm must always terminate after a finite number of steps. . n Definiteness: Each step of an algorithm must be precisely defined. It is done by well thought actions to be performed at each step of the algorithm. Also the actions are defined unambiguously for each activity in the algorithm. Effectiveness: This means that an algorithm must provide the correct answer to the problem. Generality. This means that it must solve every instance of the problem. For example, a program that computes the area of a rectangle should work on all possible dimensions of the rectangle. n 19

n n Input: Any operation you perform need some beginning value/quantities associated with different activities in the operation. So the value/quantities are given to the algorithm before it begins. Output: An algorithm must terminate, the result may be obtained at different stages of the algorithm. 20

Example Design an algorithm to add these test scores: 26, 49, 98, 87, 62, 75 and obtain the Average score 1. Start 2. Sum = 0 3. Input 26, 49, 98, 87, 62, 75 4. Sum = 26+49+98+87+62+75 5. Average = Sum/6 6. Output Average 7. Stop n 21

Problem 1: Find the area of a Circle of radius r. ALGORITHM n Step 1: Step 2: Step 3: Step 4: Step 5: Start ReadInput the Radius Area PI * Sqr(r) // Calculation of area Print Area Stop 22

n n n n Problem 2: Write an algorithm to read two numbers and find their sum. Inputs to the algorithm: Algorithm Step 1: Start Step 2: ReadInput the first num 1 Step 3: ReadInput the second num 2 Step 4: sum num 1 + num 2 Step 5: Print Sum Step 6: Stop 23

Algorithm Analysis We can have three cases to analyse an algorithm 1) Worst Case 2) Average Case 3) Best Case n Worst Case Analysis (Usually Done) n In the worst case analysis, we calculate upper bound on running time of an algorithm. n We must know the case that causes maximum number of operations to be executed. For Linear Search, the worst case happens when the element to be searched (x in the above code) is not present in the array n 24

n n Average Case Analysis (Sometimes done) In average case analysis, we take all possible inputs and calculate computing time for all of the inputs. Sum all the calculated values and divide the sum by total number of inputs. We must know (or predict) distribution of cases. For the linear search problem, let us assume that all cases are uniformly distributed (including the case of x not being present in array). 25

n n Best Case Analysis (Bogus) In the best case analysis, we calculate lower bound on running time of an algorithm. We must know the case that causes minimum number of operations to be executed. In the linear search problem, the best case occurs when x is present at the first location. The number of operations in the best case is constant (not dependent on n). So time complexity in the best case would be Θ(1) 26

Essential Elements of a Good Representation Show the Logic. Your algorithm representation should focus on the logic of the problem, and not the logic of the eventual implementation. 2. Reveal the Flow Most problems, especially if they are intended to be solved with the aid of a computer program, involve flow control. 3. Be Expandable and Collapsible Our algorithm representation should be flexible and allow us to readily collapse it so as to show less detail and focus on the more abstract elements of the algorithm or to expand it so as to get as detailed as necessary in order to actually implement the solution. 27

4. Aid in Implementation At the end of the day, the goal is usually to actually implement a solution to the problem being solved. If our method of representing our algorithm does not lend itself to an orderly implementation of that algorithm, then our method is seriously flawed. Conversely, if our method of representation lends itself to a systematic implementation of the algorithm, then our method is extremely useful 5. Implementation Independence From this point forward, we will restrict the discussion to algorithms that are intended for eventual implementation using a computer program - but the concepts described can be readily generalized to any type of implementation and you should read them with the intent of grasping those generalized concepts. 28

Tools for representing Algorithm n n n Ø Ø Ø There are two tools for representing an Algorithm Pseudocode Flowchart Pseudocode: Pseudocode is one of the tools that can be used to write a preliminary plan that can be developed into a computer program. Pseudocode is a generic way of describing an algorithm without use of any specific programming language syntax. It is, as the name suggests, pseudo code —it cannot be executed on a real computer, but it models and resembles real programming code 29

Pseudocode Pseudo code is an informal language that helps programmers develop algorithm without having to worry about the strict details of programing language syntax. It has the following peculiar attributes: Ø Steps are presented in a structured manner (numbered, indented, and so on) Ø No fixed syntax for most operations is required Ø Less ambiguous and more readable than natural language Ø Emphasis is on process, notation Ø Well-understood forms which allow logical reasoning about algorithm behaviour Ø It can be easily translated into a programming language. 30

Pseudocode Format n n n Action Keywords: There are three basic actions that can be carried out. The SET, GET, and PUT keywords. They are used for these actions. SET: This is an action keyword that denotes performing some operation that changes a value in memory. PUT: This is an action keyword that denotes an output operation, generally to the screen GET: This is an action keyword that denotes in input operation, generally from the keyboard.

Pseudocode Language Constructs n n The followings are the essential elements of Pseudocode language construct Computation/Assignment Ø Ø Ø n Compute var 1 as the sum of x and y Assign expression to var 2 Increment counter 1 Input/Output Ø Ø Input: Get var 1, var 2, … Output: Display var 1, var 2, … 32

n v Selection Single-Selection IF IF condition THEN (IF condition is true, then do subordinate statement 1, etc. If condition is false, then skip statements) ü ü v statement 1 etc. Double-Selection IF condition THEN (IF condition is true, then do subordinate statement 1, etc. If condition is false, then skip statements and execute statements under ELSE statement) 33

ü ü Statement 1, Statement 2, etc. ELSE (else if condition is not true, then do subordinate statement 2, etc. ) statement 2 statement 3 v SWITCH expression TO case 1: action 1 case 2: action 2 etc. default: action x 34

n n n Repetition WHILE condition (while condition is true, then do subordinate statements) statement 1 etc. DO – WHILE structure (like WHILE, but tests condition at the end of the loop. Thus, statements in the structure will always be executed at least once. ) DO statement 1 etc. 35

Pseudocode n Example 1: Write an algorithm to determine a student’s final grade and indicate whether it is passing or failing. The final grade is calculated as the average of four marks.

Pseudocode & Algorithm Pseudocode: n Input a set of 4 marks n Calculate their average by summing and dividing by 4 n if average is below 50 Print “FAIL” else Print “PASS”

Pseudocode Detailed Algorithm n Step 1: Input M 1, M 2, M 3, M 4 Step 2: GRADE (M 1+M 2+M 3+M 4)/4 Step 3: if (GRADE < 50) then Print “FAIL” else Print “PASS” endif n

Pseudocode n n Example 2 Express an algorithm to get two numbers from the user (dividend and divisor), testing to make sure that the divisor number is not zero, and displaying their quotient using pseudocode 39

n n Declare variables: dividend, divisor, quotient Prompt user to enter dividend and divisor Get dividend and divisor IF divisor is equal to zero, THEN DO n n Display error message, “divisor must be non-zero” Prompt user to enter divisor Get divisor WHILE divisor is equal to zero ENDIF Display dividend and divisor Calculate quotient as dividend/divisor Display quotient 40

Example: Pseudocode for computing miles per litre STEP OPERATIONS 1 GET VALUES OF LITRES USED, STARTING MILEAGE, ENDING MILEAGE 2 SET VALUE OF DISTANCE DRIVEN (ENDING MILEAGESTARTING MILEAGE 3 SET VALUE OF AVERAGE MILES PER LITRE TO(DISTANCE DRIVEN – LITRES USED) 4 PRINT THE VALUE OF AVERAGE MILES PER LITRE 5 STOP

FLOWCHART n § § § Flowchart is a graphical tool that diagrammatically depicts the steps and structures of an algorithm or program. A flowchart is a diagram made up of boxes, diamonds and other shapes, connected by arrows. Each shape represents a step in the process, and the arrows show the order in which they occur. Flowchart combines symbols and flow-lines, to show figuratively the operation of an algorithm. 42

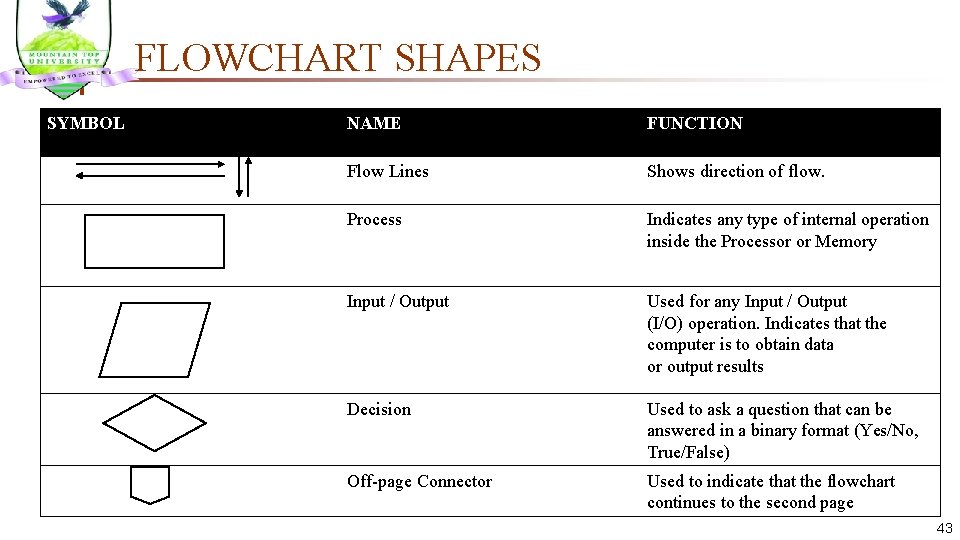
FLOWCHART SHAPES SYMBOL NAME FUNCTION Flow Lines Shows direction of flow. Process Indicates any type of internal operation inside the Processor or Memory Input / Output Used for any Input / Output (I/O) operation. Indicates that the computer is to obtain data or output results Decision Used to ask a question that can be answered in a binary format (Yes/No, True/False) Off-page Connector Used to indicate that the flowchart continues to the second page 43

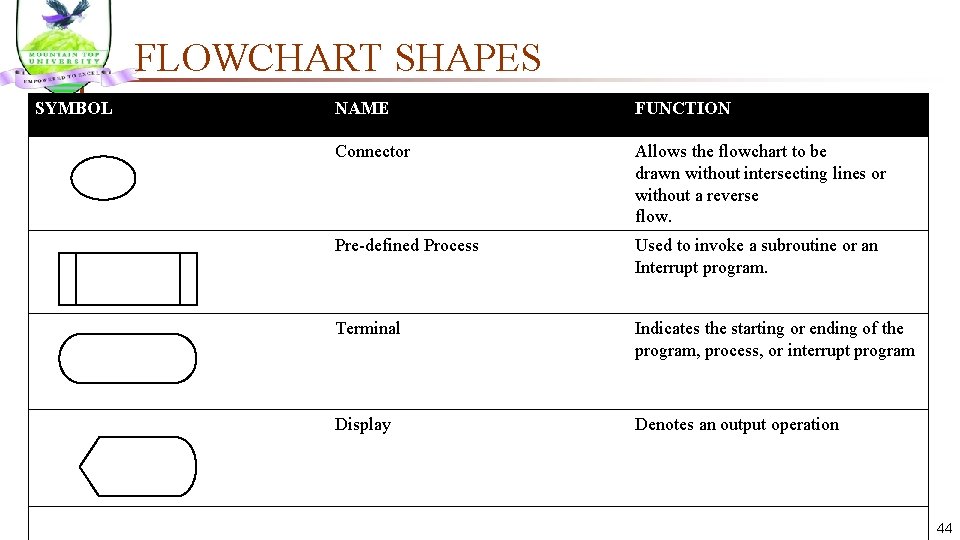
FLOWCHART SHAPES SYMBOL NAME FUNCTION Connector Allows the flowchart to be drawn without intersecting lines or without a reverse flow. Pre-defined Process Used to invoke a subroutine or an Interrupt program. Terminal Indicates the starting or ending of the program, process, or interrupt program Display Denotes an output operation 44

General Rules for flowcharting 1. All boxes of the flowchart are connected with Arrows. (Not lines) 2. Flowchart symbols have an entry point on the top of the symbol with no other entry points. The exit point for all flowchart symbols is on the bottom except for the Decision symbol. 3. The Decision symbol has two exit points; these can be on the sides or the bottom and one side. 4. Generally a flowchart will flow from top to bottom.

Advantages of Using Flowcharts: n n n Communication: Flowcharts are better way of communicating the logic of a system to all concerned. Effective analysis: With the help of flowchart, problem can be analysed in more effective way. Proper documentation: Program flowcharts serve as a good program documentation, which is needed for various purposes. Efficient Coding: The flowcharts act as a guide or blueprint during the systems analysis and program development phase. Proper Debugging: The flowchart helps in debugging process. Efficient Program Maintenance: The maintenance of

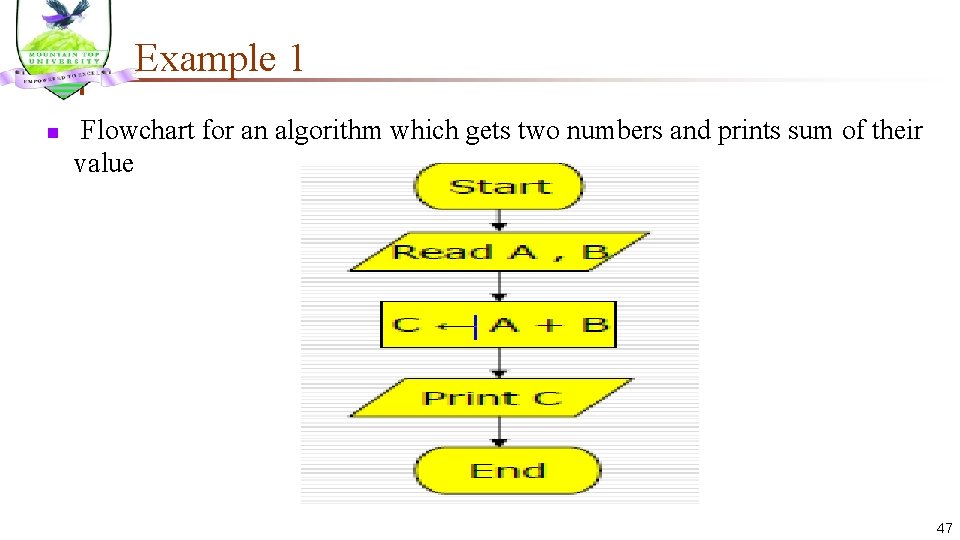
Example 1 n Flowchart for an algorithm which gets two numbers and prints sum of their value 47

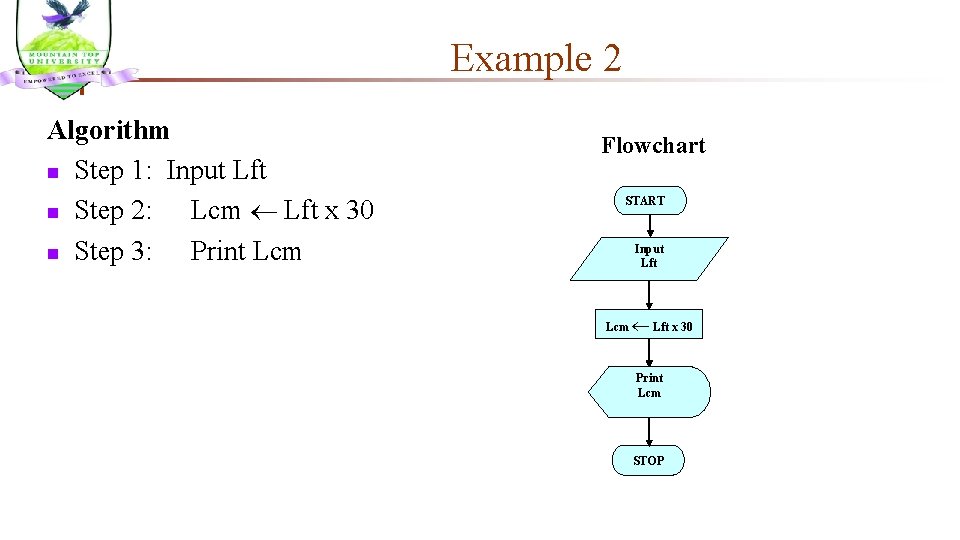
Example 2 Write an algorithm and draw a flowchart to convert the length in feet to centimeter. Pseudocode: n Input the length in feet (Lft) n Calculate the length in cm (Lcm) by multiplying LFT with 30 n Print length in cm (LCM) n

Example 2 Algorithm n Step 1: Input Lft n Step 2: Lcm Lft x 30 n Step 3: Print Lcm Flowchart START Input Lft Lcm Lft x 30 Print Lcm STOP

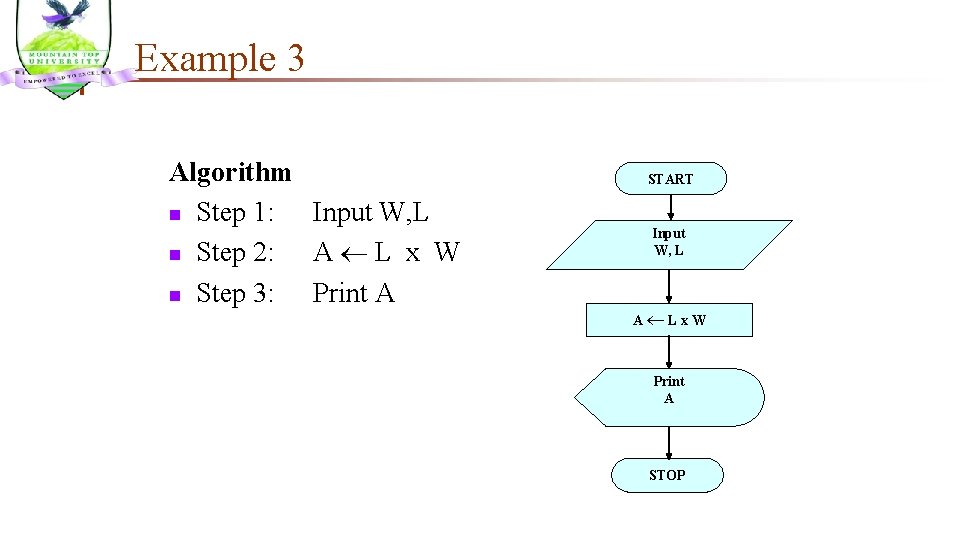
Example 3 Write an algorithm and draw a flowchart that will read the two sides of a rectangle and calculate its area. Pseudocode n Input the width (W) and Length (L) of a rectangle n Calculate the area (A) by multiplying L with W n Print A

Example 3 Algorithm n Step 1: Input W, L n Step 2: A L x W n Step 3: Print A START Input W, L A L x W Print A STOP

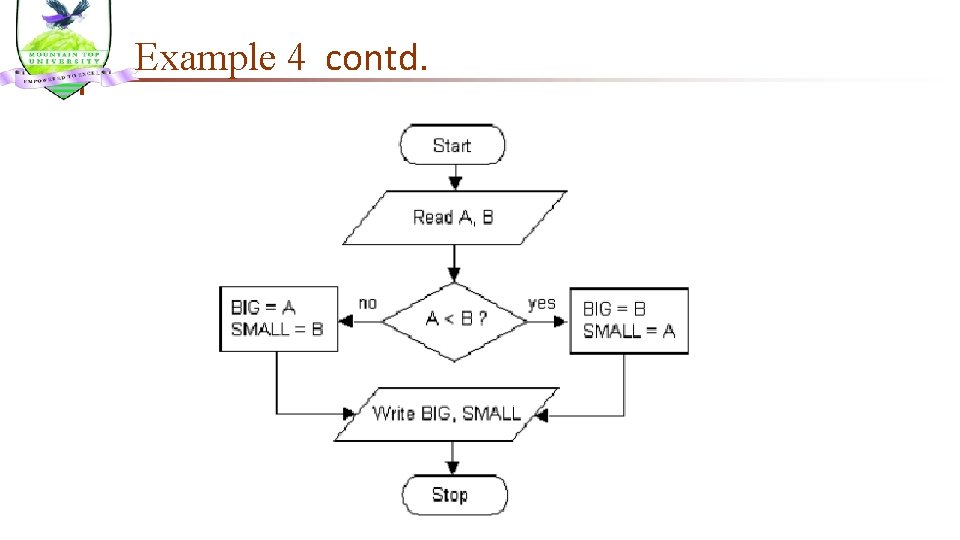
Example 4 Write an algorithm to find the larger number between A and B Algorithm: 1. Read A, B 2. If A is less than B 3. BIG=B, SMALL = A 4. Else 5. BIG=A, SMALL = B 6. Write BIG, SMALL n n The flowchart is represented as:

Example 4 contd.

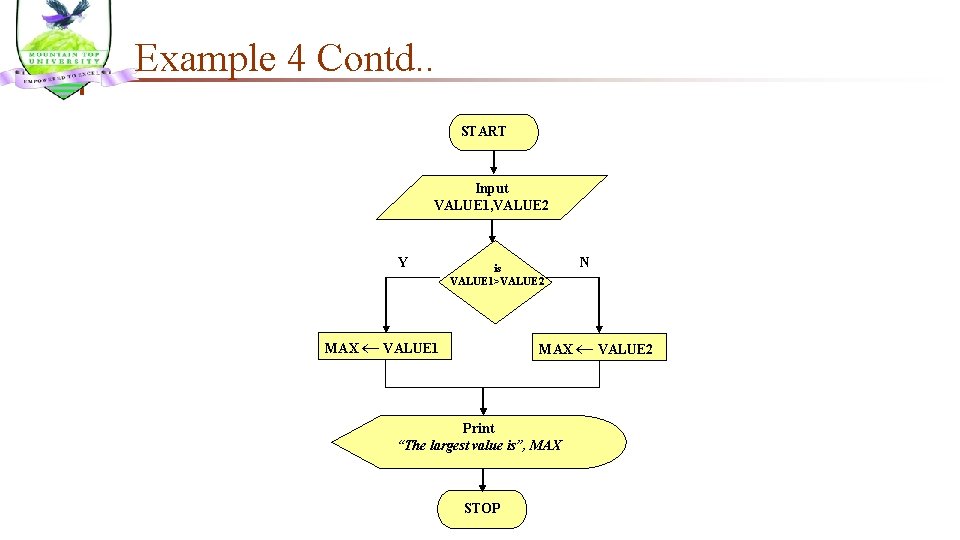
ANOTHER VERSION OF EXAMPLE 4 Write an algorithm that reads two values, determines the largest value and prints the largest value with an identifying message. ALGORITHM Step 1: Input VALUE 1, VALUE 2 Step 2: if (VALUE 1 > VALUE 2) then MAX VALUE 1 else MAX VALUE 2 endif Step 3: Print “The largest value is”, MAX n

Example 4 Contd. . START Input VALUE 1, VALUE 2 Y is VALUE 1>VALUE 2 MAX VALUE 1 N MAX VALUE 2 Print “The largest value is”, MAX STOP

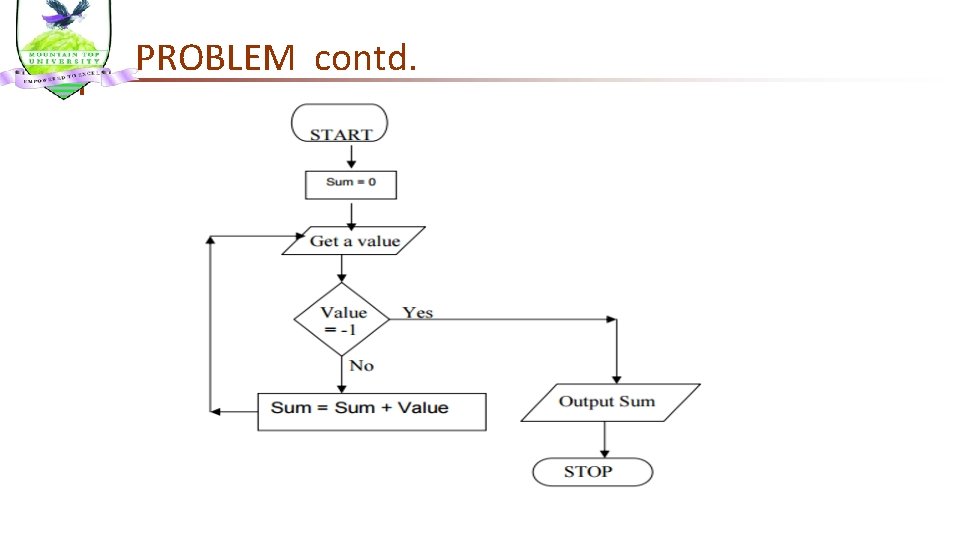
PROBLEM Considering this algorithm, 1. Start 2. Sum = 0 3. Get a value 4. If the value is equal to – 1, 5. Output Sum 6. Else 7. Sum = Sum + value 8. Go to step 3 to get next value 9. Stop n Draw the flowchart for this algorithm n

PROBLEM contd.

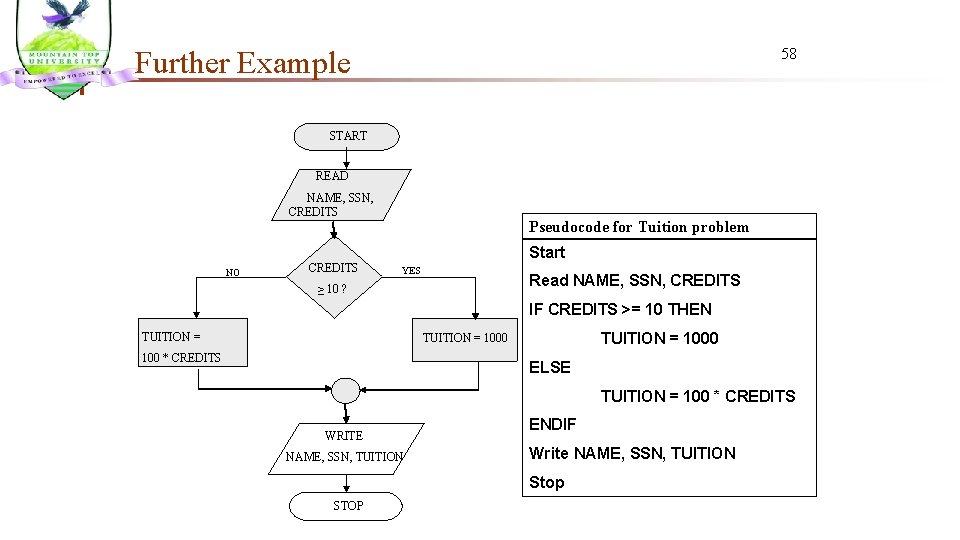
Further Example 58 START READ NAME, SSN, CREDITS NO CREDITS Pseudocode for Tuition problem Start YES ≥ 10 ? Read NAME, SSN, CREDITS IF CREDITS >= 10 THEN TUITION = 1000 100 * CREDITS ELSE TUITION = 100 * CREDITS WRITE NAME, SSN, TUITION ENDIF Write NAME, SSN, TUITION Stop STOP

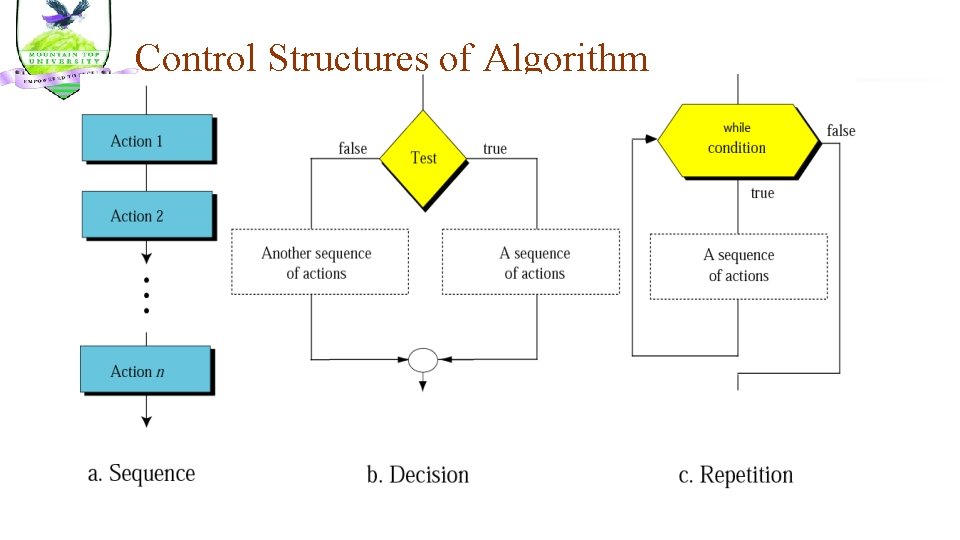
Control Structures of Algorithm n n n A control structure is a block of programming that analyses variables and chooses a direction in which to go based on given parameters. What kind of control structures are necessary to describe algorithm? Types of Control Structure Ø Ø Ø 1. Sequence Selection Iteration (Repetition) a way that, no condition step is required.

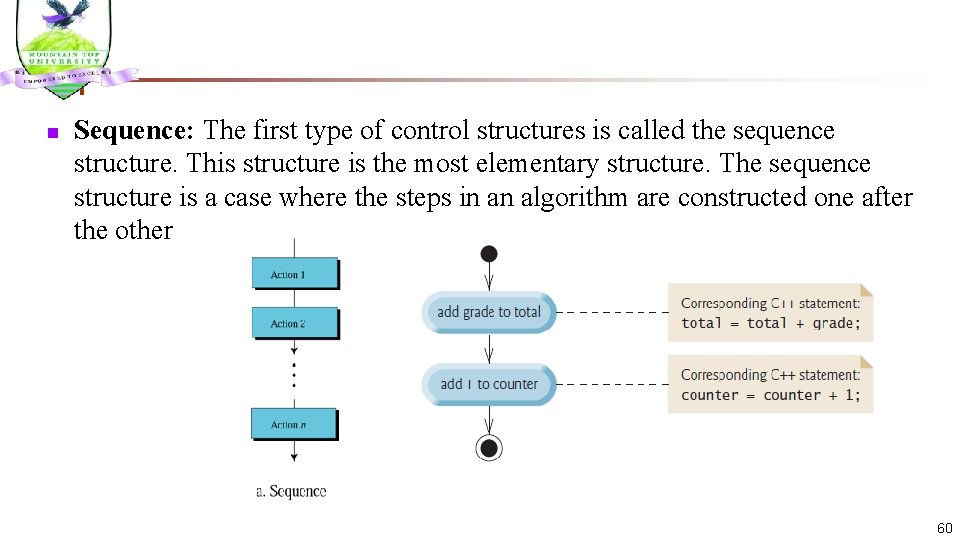
n Sequence: The first type of control structures is called the sequence structure. This structure is the most elementary structure. The sequence structure is a case where the steps in an algorithm are constructed one after the other 60

Control Structures of Algorithm: Sequence n n 1. 2. 3. 4. 5. 6. 7. For example, suppose you are required to design an algorithm for finding the average of six numbers. and the sum of the numbers is given. The algorithm will be as follows: Start Set Sum = 0 Input X 1, X 2 … X 6 sum = X + X …+ X 1 2 6 Set Average = Sum / 6 Output Average Stop

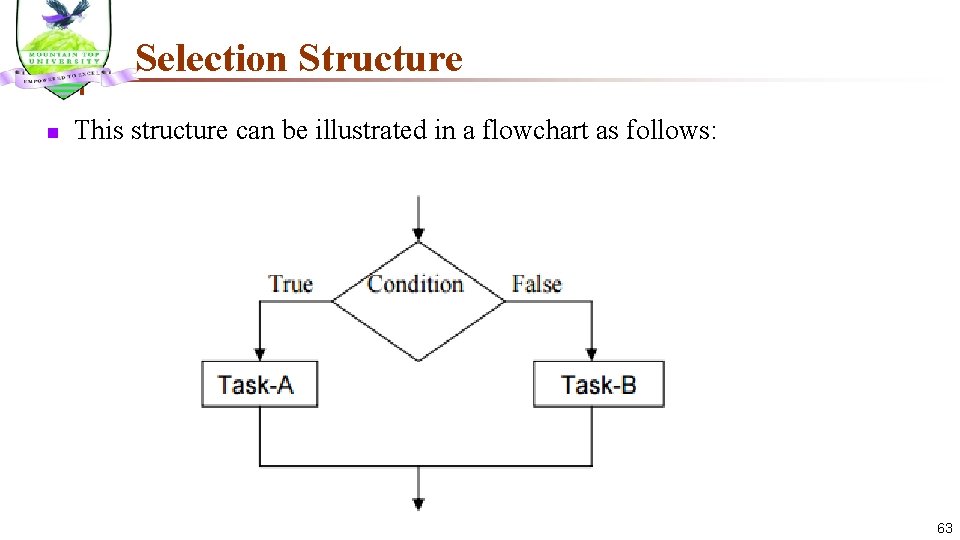
Selection Structure n Selection Structure: The selection structure also known as decision structure is a case in the algorithm where one has to make a choice of two alternatives by making a decision depending on a given condition. A selection structure takes the form: If condition is true Then do task A else Do Task-B n

Selection Structure n This structure can be illustrated in a flowchart as follows: 63

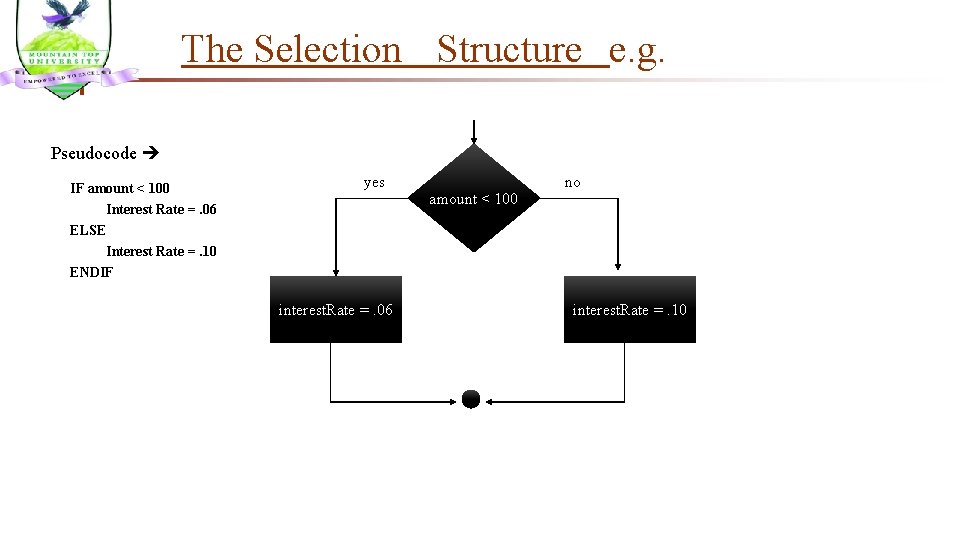
The Selection Structure e. g. Pseudocode IF amount < 100 Interest Rate =. 06 yes amount < 100 no ELSE Interest Rate =. 10 ENDIF interest. Rate =. 06 interest. Rate =. 10

Selection Structure n The selection requires the following: Ø Ø n n Choose alternative actions as a result of testing a logical condition Produce code to test a sequence of logical tests In making choices, IF statement is used together with logical operators to test for true or false. The logical operators used are: Ø Ø = is equal to <= is less than or equal > is greater than <> is not equal to < is less than >= is greater than or equal

Iteration or Repetition structures 3. Iteration or Repetition structures: The iteration structure can be implemented using • Repeat Until Loop • The While Loop • The For Loop n Any program instruction that repeats some statement or sequence of statements a number of times is called an iteration or a loop. The commands used to create iterations or loops are all based on logical tests.

Iteration or Repetition structures • Repeat Until Loop The syntax is REPEAT A statement or block of statements UNTIL a true condition n For example, A program repeatedly asking for an entry of a number in the range 1 to 100 until a valid number is entered. REPEAT Output “Enter a number between 1 and 100” UNTIL number < 1 OR number > 100

Iteration or Repetition structures The While Loop The second type of iteration. This type of conditional loop tests for terminating condition at the beginning of the loop. In this case no action is performed at all if the first test causes the terminating condition to evaluate as false. n The syntax is: WHILE (a condition is true) A statement or block of statements ENDWHILE

Control Structures of Algorithm

Iteration or Repetition structures • The For Loop: The third type of iteration. This, in its simplest form, uses an initialisation of the variable as a starting point, a stop condition depending on the value of the variable. The variable is incremented on each iteration until it reaches the required value. The syntax is: FOR (starting state, stopping condition, increment) Statements ENDFOR n For example: FOR (n = 1, n <= 4, n + 1) Output “loop”, n ENDFOR

Control Structures of Algorithm The fragment of code will produce the output Loop 1 Loop 2 Loop 3 Loop 4 n n n In the example, n is usually referred as the loop variable, or counter, or index of the loop. Example : Write an algorithm to calculate the sum and average of a series of numbers.

QUIZ Instruction: Answer any two questions. Time allowed: 20 minutes 1. 2. 3. Design an algorithm and the corresponding flowchart for adding the odd integers between 1 and 99 Write an algorithm to determine a student’s final grade and indicate whether passed or failed. The final grade is calculated as the average of four marks. If a = 1, b = 3, and x = 7, What is the value of x when the loop terminates? for(k = a; k < = b; k + 1) { x = x - k; } // show your steps 72

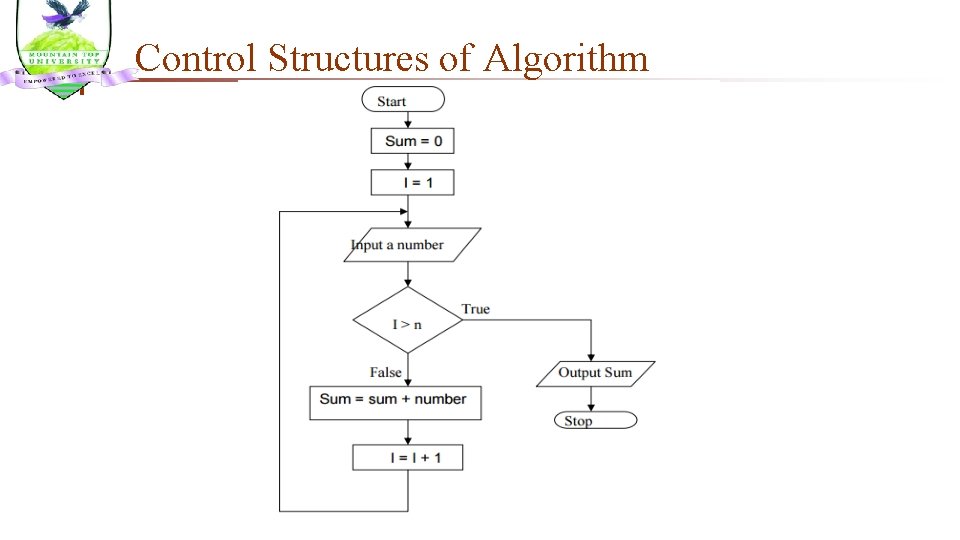
Control Structures of Algorithm n Example: Design an algorithm and the corresponding flowchart for finding the sum of n numbers. Algorithm 1. Start 2. Sum = 0 3. Input n 4. For(I = 1, I <= n, I+1) 5. Input a number 6. Sum = Sum + number 7. ENDFOR 8. Output Sum 9. Stop n

Control Structures of Algorithm n n In this example, we compare I with n to check whether we have exhausted the numbers or not in order to stop the computation of the sum (or to stop the iteration structure). In such a case, I is referred to as a counter. The corresponding flowchart will be as follows:

Control Structures of Algorithm

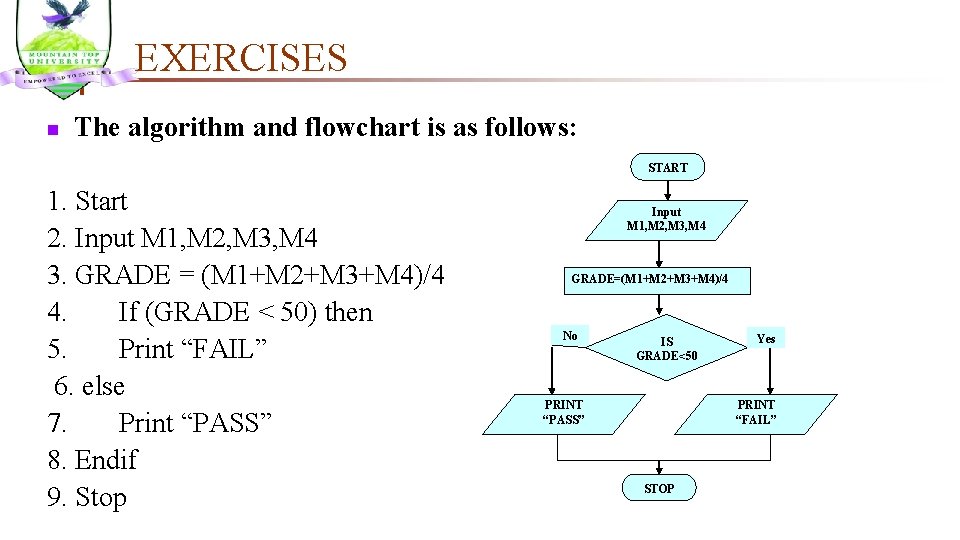
EXERCISES EX 1: Write an algorithm to determine a student’s final grade and indicate whether passed or failed. The final grade is calculated as the average of four marks. Pseudocode: 1. Start 2. Get a set of 4 marks 3. Set their average by summing and dividing by 4 4. If average is below 50 5. Put “FAIL” 6. else 7. Put “PASS” 8. Stop

EXERCISES n The algorithm and flowchart is as follows: START 1. Start 2. Input M 1, M 2, M 3, M 4 3. GRADE = (M 1+M 2+M 3+M 4)/4 4. If (GRADE < 50) then 5. Print “FAIL” 6. else 7. Print “PASS” 8. Endif 9. Stop Input M 1, M 2, M 3, M 4 GRADE=(M 1+M 2+M 3+M 4)/4 No IS GRADE<50 PRINT “PASS” Yes PRINT “FAIL” STOP

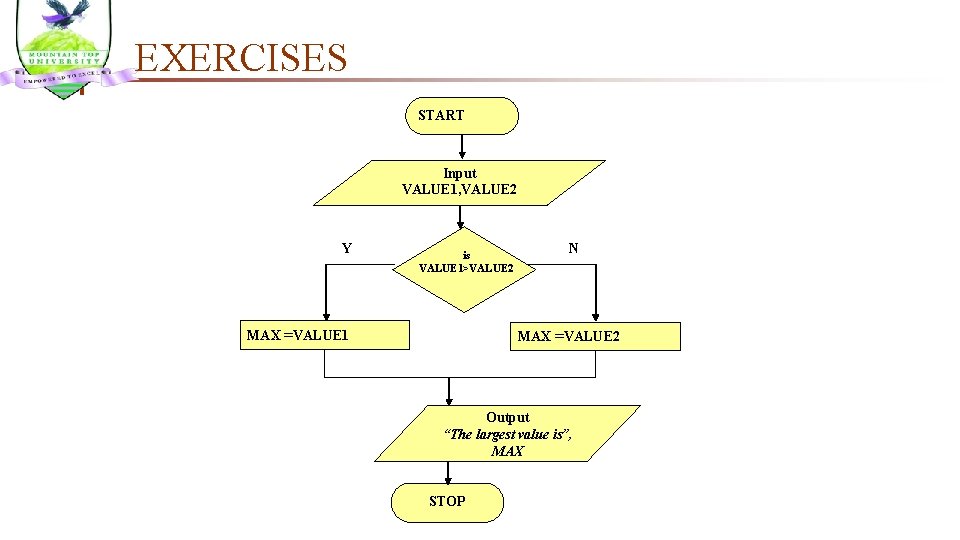
EXERCISES Ex 2: Write an algorithm that reads two values, determines the larger value and prints the larger value with an identifying message. ALGORITHM 1. Start 2. Input VALUE 1, VALUE 2 3. If (VALUE 1 > VALUE 2) then 4. MAX = VALUE 1 5. else 6. MAX = VALUE 2 7. Endif 8. Output “The largest value is”, MAX 9. Stop

EXERCISES START Input VALUE 1, VALUE 2 Y is VALUE 1>VALUE 2 MAX =VALUE 1 N MAX =VALUE 2 Output “The largest value is”, MAX STOP

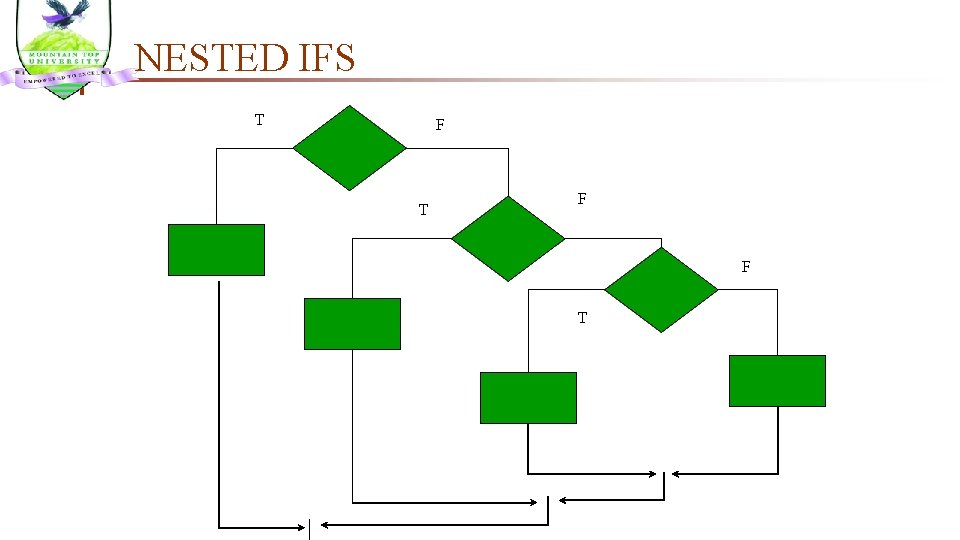
NESTED IFS n EX 3: given three numbers say N 1, N 2 & N 3 write an algorithm to find the largest number 1. Start 2. Input N 1, N 2, N 3 3. If (N 1>N 2) then 4. if (N 1>N 3) then 5. MAX N 1 // [N 1>N 2, N 1>N 3] 6. else 7. MAX N 3 // [N 3>N 1>N 2] 8. endif 9. else 10. if (N 2>N 3) then 11. MAX N 2 // [N 2>N 1, N 2>N 3] 12. else 13. MAX N 3 // [N 3>N 2>N 1] 14. endif 15. endif

NESTED IFS 16. Output “The largest number is”, MAX 17. Stop

NESTED IFS T F F T

EXERCISES EX 4: Write an algorithm and draw a flowchart that will calculate the roots of a quadratic equation Hint: d = sqrt (b²-4 ac), and the roots are: x 1 = (–b + d)/2 a and x 2 = (–b – d)/2 a START 1. Start Input a, b, c 2. Input a, b, c d =sqrt (b² – 4 ac) 3. Let d = sqrt (b²-4 ac) x 1 =(–b + d) / (2 a) 4. Let x 1 = (–b + d) / (2 a) x 2 = (–b – d) / (2 a) 5. Let x 2 = (–b – d) / (2 a) Output 6. Output x 1, x 2 7. Stop STOP

CALCULATIONS ON FOR LOOP QUESTION : If a=1, b=3, and x=7, What is the value of x when the loop terminates? for(k = a; k < = b; k++) { x=x-k; } SOLUTION First iteration (k=1, x=7) Test: 1<=3 is true Execute: x= 7 -1= 6

CALCULATIONS ON FOR LOOP • Second iteration (k=2, x=6) Test: 2<=3 is true Execute: x= 6 -2= 4 • Third iteration (k=3, x=4) Test: 3<=3 is true Execute: x= 4 -3= 1 • Fourth iteration (k=4, x=1) Test: 4<=3 is false – EXIT loop.

CALCULATIONS ON FOR LOOP QUESTION : If a=2, b=4, x=1, and y=9, what are the values of x and y when the loop terminates? for(k=a; k<b; k++) { x=x+k; y=y-x; } SOLUTION • First iteration (k=2, x=1, y=9) test: 2<4 is true execute: x= 1+2 =3

CALCULATIONS ON FOR LOOP • Second iteration (k=3, x=3, y=6) Test: 3<4 is true Execute: x= 3+3 =6 y= 6 -6= 0 • Third iteration (k=4, x=6, y=0) test: 4<3 is false n EXIT loop n Hence, the values of x and y when the loop terminates are 6 and 0

CALCULATIONS ON WHILE LOOP QUESTION: What is the value of p when the loop terminates? p = 0; t = 1; n = 10; while(n > t) { p = p + n * t; t = t + 4; }

CALCULATIONS ON WHILE LOOP SOLUTION • First iteration (t=1, p=0) Test: 10>1 is true Execute: p = 0+10*1 = 10 t = 1+4 = 5 • Second iteration (t=5, p=10) Test: 10>5 is true Execute: p = 10+10*5 = 60 t = 5+4 = 9

CALCULATIONS ON WHILE LOOP • Third iteration (t=9, p=60) Test: 10>9 is true Execute: p = 60+10*9 = 150 t = 9+4 = 13 • Fourth iteration (t=13, p=150) Test: 10>13 is false n EXIT loop Hence, the value of p when the loop terminates is 150

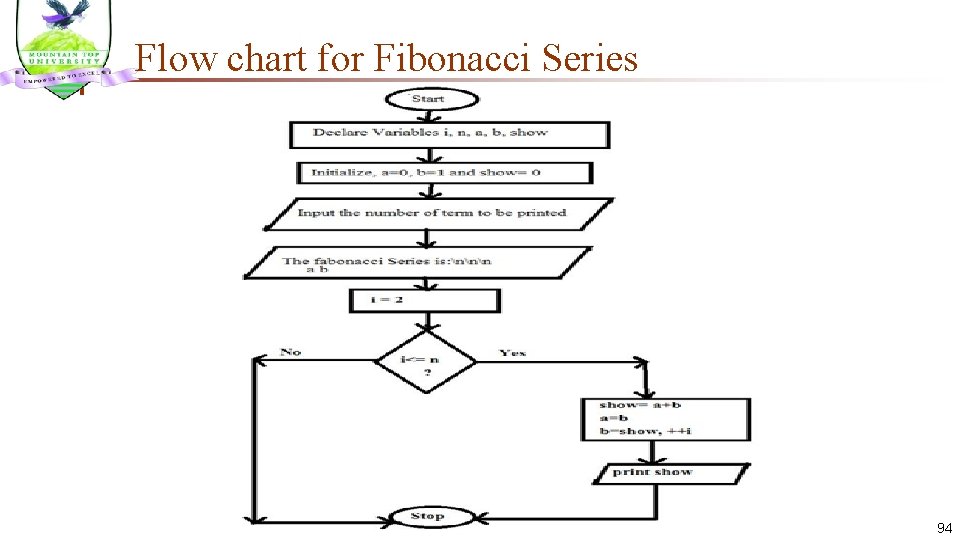
Fibonacci Seris n n The Fibonacci numbers upto certain term can be represented as: 1, 1, 2, 3, 5, 8, 13, 21, 34, First Term = 0 Second term = 1 Third Term = First + Second = 0+1 =1 Fourth term = Second + Third =1+1 = 2 Fifth Term = Third + Fourth = 2+1 = 3 Sixth Term= Fourth + Fifth = 3+2 = 5 Seventh Term = Fifth + Sixth = 3+5 = 8 Eighth Term = Sixth + Seventh = 5+8 = 13 … and so on to infinity! 92

Algorithm for Fibonacci Series n n Start Declare variables i, a, b , show Initialize the variables, a=0, b=1, and show =0 n Enter the number of terms of Fibonacci series to be printed n Print First two terms of series n Use loop for the following steps show=a+b a=b b=show increase value of i each time by 1 print the value of show n n End 93

Flow chart for Fibonacci Series 94

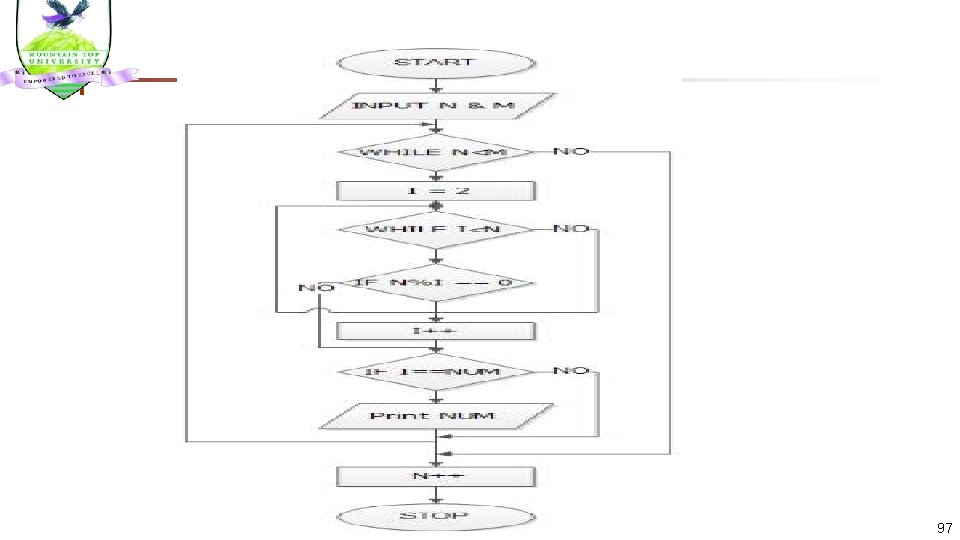
PRIME NUMBERS n Design an algorithm and draw corresponding flowchart to find all the prime numbers between two given numbers ‘m’ and ‘n’, where m, n > 0. 10 Pseudo code n Input N and M n While N is smaller than M n Initialize I to 2 n While I is smaller than N If N is divisible by I skip loop Increment I If N is equal to I Print N n Increment N 95

Detailed Algorithm: n Step 1: Input M & N n Step 2: While (M <N) Step 3 I=2 n Step 4: While (I<M) n Step 5: IF M%I == 0 Step 6 goto Step 7 n Step 7: I++ n Step 8: IF I==NUM n Print NUM Step 9: M++ n 96

97

INTRODUCTION TO C PROGRAMING LANGUAGE n Programing and Programing Languages Programmers write instructions in various programing languages, some directly understandable by computers and others requiring intermediate translation steps. Hundreds of computer languages are in used today. These may be divided into three general types i. Machine Languages ii. Assembly Languages iii. High-level languages Machine Language is the “natural language “ of a computer and as such is defined by its hardware design, machine Language generally consists of strings of numbers ( ultimately reduced to 1 s and 0 s) ü 98

n Assembly Languages: In order to express operations more abstractly, assembly languages were developed. Ø n These languages have simple mnemonic instructions that directly map to a sequence of machine language operations. For example, the MOV instruction moves data into a register, the ADD instruction adds the contents of two registers together. Programs written in assembly language are translated to machine code using an assembler program High-level Languages were developed between 1950 s and 60 s. These languages provide mechanisms, such as subroutines and conditional looping constructs, which greatly enhance the structure of a program, making it easier to express the progression of instruction execution 99

n n HISTROY OF C C language was evolved from B by Denis Ritchie at Bell Laboratories and was originally implemented in 1972. it initially became widely known as the development language of the UNIX operating system. Today, most of the code for general-purpose operating systems is written in C or C++ Definition of some basic terms in C Reserved words: there are certain reserved words that have a predefined meaning in C. they cannot be arbitrary redefined by the programmer e. g. Int, for, float, #include, 100

n n n Identifiers Identifiers (i. e. , variable names, function names, etc) are made up of letters and digits, and are case-sensitive. The first character of an identifier must be a letter, which includes underscore ( _ ). The C language has 32 keywords which are reserved and may not be used as identifiers (eg, int, while, etc). Furthermore, it is a good idea to avoid redefining identifiers used by the C standard library (such as standard function names, etc). 101

Types n C is a typed language. Each variable is given a specific type which defines what values it can represent, how its data is stored in memory, and what operations can be performed on it. By forcing the programmer to explicitly define a type for all variables and interfaces, the type system enables the compiler to catch type-mismatch errors, thereby preventing a significant source of bugs. There are three basic types in the C language: characters, and integer and floating-point numbers. 102

Data types n n Data types in C refer to an extensive system used for declaring variables or functions of different types. The type of a variable determines how much space it occupies in storage and how the bit pattern stored is interpreted. The types in C can be classified as follows: 103

Types in C 104

Integer Types n The following table provides the details of standard integer types with their storage sizes and value ranges 105

Integer Types 106

n To get the exact size of a type or a variable on a particular platform, you can use the sizeof operator. #include <stdio. h> #include <limits. h> int main() { printf("Storage size for int : %d n", sizeof(int)); return 0; } 107

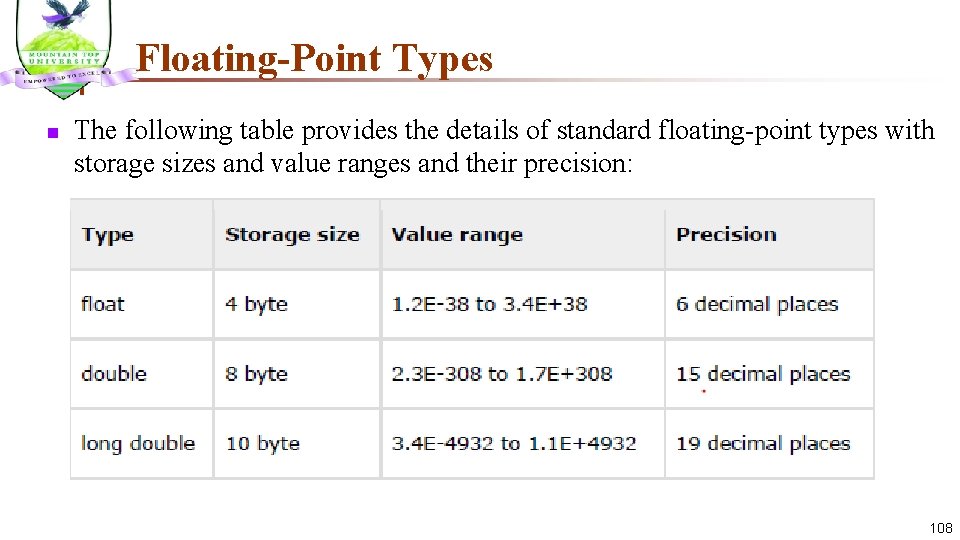
Floating-Point Types n The following table provides the details of standard floating-point types with storage sizes and value ranges and their precision: 108

Floating-Point Types n The header file float. h defines macros that allow you to use these values and other details about the binary representation of real numbers in your programs. The following example prints the storage space taken by a float type and its range values: #include <stdio. h> #include <float. h> int main() { printf("Storage size for float : %d n", sizeof(float)); printf("Minimum float positive value: %E n", FLT_MIN ); printf("Maximum float positive value: %E n", FLT_MAX ); printf("Precision value: %d n", FLT_DIG ); return 0; 109

The void Type n The void type specifies that no value is available. It is used in three kinds of situations: 110

Variables n n n A variable is nothing but a name given to a storage area that our programs can manipulate. Each variable in C has a specific type, which determines the size and layout of the variable's memory; The name of a variable can be composed of letters, digits, and the underscore character. It must begin with either a letter or an underscore. Upper and lowercase letters are distinct because C is case-sensitive. 111

Variable definition in C n n A variable definition tells the compiler where and how much storage to create for the variable. A variable definition specifies a data type and contains a list of one or more variables of that type as follows: type variable_list; Here, type must be a valid C data type including char, w_char, int, float, double, bool, or any user-defined object; int i, j, k; char c, ch; float f, salary; double d; 112

Example #include <stdio. h> // Variable declaration: extern int a, b; extern int c; extern float f; int main () { /* variable definition: */ int a, b; int c; float f; 113

Example /* actual initialization */ a = 10; b = 20; c = a + b; printf("value of c : %d n", c); f = 70. 0/3. 0; printf("value of f : %f n", f); return 0; } 114

Constants and literals n n n Constants refer to fixed values that the program may not alter during its execution. These fixed values are also called literals. Constants can be of any of the basic data types like an integer constant, a floating constant, a character constant, or a string literal. There are enumeration constants as well. Constants are treated just like regular variables except that their values cannot be modified after their definition. 115

Integer Literals n n n An integer literal can be a decimal, octal, or hexadecimal constant. A prefix specifies the base or radix: 0 x or 0 X for hexadecimal, 0 for octal, and nothing for decimal. An integer literal can also have a suffix that is a combination of U and L, for unsigned and long, respectively. The suffix can be uppercase or lowercase and can be in any order. Here are some examples of integer literals: 212 /* Legal */ 215 u /* Legal */ 0 x. Fee. L /* Legal */ 078 /* Illegal: 8 is not an octal digit */ 032 UU /* Illegal: cannot repeat a suffix */ 116

Integer Literals n The followings are examples of various types of integer literals 117

Floating-point Literals n n A floating-point literal has an integer part, a decimal point, a fractional part, and an exponent part. You can represent floating point literals either in decimal form or exponential form. While representing decimal form, you must include the decimal point, the exponent, or both; while representing exponential form, you must include the integer part, the fractional part, or both. The signed exponent is introduced by e or E. 118

Floating-point Literals Here are some examples of floating-point literals: n 3. 14159 /* Legal */ n 314159 E-5 L /* Legal */ n 510 E /* Illegal: incomplete exponent */ n 210 f /* Illegal: no decimal or exponent */ n. e 55 /* Illegal: missing integer or fraction */ 119

Character Literals n n n Character literals are enclosed in single quotes, e. g. , 'x' can be stored in a simple variable of char type. A character literal can be a plain character (e. g. , 'x'), an escape sequence (e. g. , 't'), or a universal character (e. g. , 'u 02 C 0'). There are certain characters in C that represent special meaning when preceded by a backslash, for example, newline (n) or tab (t). Here, you have a list of such escape sequence codes: 120

Character Literals n n n n n Escape sequence \ a b f n r t v Meaning character Alert or bell Backspace Form feed Newline Carriage return Horizontal tab Vertical tab 121

String Literals n n n String literals or constants are enclosed in double quotes "". A string contains characters that are similar to character literals: plain characters, escape sequences, and universal characters. You can break a long line into multiple lines using string literals and separating them using whitespaces. Here are some examples of string literals. All the three forms are identical strings. "hello, dear" "hello, dear" "hello, " "d" "ear" 122

Defining Constants There are two simple ways in C to define constants: � Using #define preprocessor � Using const keyword The #define Preprocessor n Given below is the form to use #define preprocessor to define a constant: n #define identifier value n 123

Example #include <stdio. h> #define LENGTH 10 #define WIDTH 5 #define NEWLINE 'n' int main() { int area; area = LENGTH * WIDTH; printf("value of area : %d", area); printf("%c", NEWLINE); return 0; } 124

n n The const Keyword You can use const prefix to declare constants with a specific type as follows: const type variable = value; #include <stdio. h> int main() { const int LENGTH = 10; const int WIDTH = 5; 125

const char NEWLINE = 'n'; int area; area = LENGTH * WIDTH; printf("value of area : %d", area); printf("%c", NEWLINE); return 0; } 126

Arithmetic Operators n The following table shows all the arithmetic operators supported by the C language. Assume variable A holds 10 and variable B holds 20, then: 127

Arithmetic Operators -- Decrement operator decreases the integer value by one. A-- = 9 n EXAMPLE #include <stdio. h> n main() { int a = 21; int b = 10; int c ; c = a + b; printf("Line 1 - Value of c is %dn", c ); c = a - b; printf("Line 2 - Value of c is %dn", c ); c = a * b; 128

EXAMPLE (continued…) printf("Line 3 - Value of c is %dn", c ); c = a / b; printf("Line 4 - Value of c is %dn", c ); c = a % b; printf("Line 5 - Value of c is %dn", c ); c = a++; printf("Line 6 - Value of c is %dn", c ); c = a--; printf("Line 7 - Value of c is %dn", c ); } 129

Relational Operators n The following table shows all the relational operators supported by C. Assume variable A holds 10 and variable B holds 20, then: 130

Relational Operators 131

Example Try the following example to understand all the relational operators available in C: #include <stdio. h> n main() { int a = 21; int b = 10; int c ; if( a == b ) { printf("Line 1 - a is equal to bn" ); } else 132

EXAMPLE (continued…) { printf("Line 1 - a is not equal to bn" ); } if ( a < b ) { printf("Line 2 - a is less than bn" ); } else { printf("Line 2 - a is not less than bn" ); } if ( a > b ) { printf("Line 3 - a is greater than bn" ); } else 133

{ printf("Line 3 - a is not greater than bn" ); } /* Lets change value of a and b */ a = 5; b = 20; if ( a <= b ) { printf("Line 4 - a is either less than or equal to bn" ); } if ( b >= a ) { printf("Line 5 - b is either greater than or equal to bn" ); } } 134

Logical Operators n Following table shows all the logical operators supported by C language. Assume variable A holds 1 and variable B holds 0, then 135

Logical Operators n n Example Try the following example to understand all the logical operators available in C: 136

Example #include <stdio. h> main() { int a = 5; int b = 20; int c ; if ( a && b ) { printf("Line 1 - Condition is truen" ); } if ( a || b ) { printf("Line 2 - Condition is truen" ); } 137

/* lets change the value of a and b */ a = 0; b = 10; if ( a && b ) { printf("Line 3 - Condition is truen" ); } else { printf("Line 3 - Condition is not truen" ); } if ( !(a && b) ) { printf("Line 4 - Condition is truen" ); } } 138

Bitwise Operators n Bitwise operators work on bits and perform bit-by-bit operation. The truth table for &, |, and ^ is as follows: 139

Bitwise Operators n Ø Ø Ø n Assume A = 60 and B = 13; in binary format, they will be as follows: A = 0011 1100 B = 0000 1101 A&B = 0000 1100 A|B = 0011 1101 A^B = 0011 0001 ~A = 1100 0011 The following table lists the bitwise operators supported by C. Assume variable ‘A’ holds 60 and variable ‘B’ holds 13, then: 140

Bitwise Operators supported by C 141

1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. #include <stdio. h> main() { unsigned int a = 60; unsigned int b = 13; int c = 0; c = a & b; printf("Line 1 - Value of c is %dn", c ); c = a | b; printf("Line 2 - Value of c is %dn", c ); c = a ^ b; printf("Line 3 - Value of c is %dn", c ); c = ~a; printf("Line 4 - Value of c is %dn", c ); } /* 60 = 0011 1100 */ /* 13 = 0000 1101 */ /* 12 = 0000 1100 */ /* 61 = 0011 1101 */ /* 49 = 0011 0001 */ /*-61 = 1100 0011 */ 142

n n Suppose a, b, c, d and e are numeric type variables that have been assigned the following values Variable Type value a Integer 8 b Integer 5 c Float 4. 3 d Float 0. 8 e Float -2. 2 These variables are used in the following numerical expression. Determine the type of each expression and the value that it represents i. (b-a)/sqr(d-e) ii. round((c=d)/e) iii. (a div b) / (a mod b) Iv. (a-2* b) * truc (3 * c-d + 2 * 2) 143

CONTROL STRUCTURE n n A control structure is a block of programming that analyzes variables and chooses a direction in which to go based on given parameters Types of Control Structure Ø Ø Ø Sequence Selection Iteration (Repetition) 144

if Selection Structure n Selection structure n n Choose among alternative courses of action Pseudocode example: If student’s grade is greater than or equal to 60 Print “Passed” n If the condition is true n n If the condition is false n n Print statement executed, program continues to next statement Print statement ignored, program continues Indenting makes programs easier to read n C ignores whitespace characters (tabs, spaces, etc. ) 145

if Selection Structure n Translation into C If student’s grade is greater than or equal to 60 Print “Passed” if ( grade >= 60 ) printf(“passed”) n Diamond symbol (decision symbol) n n Indicates decision is to be made Contains an expression that can be true or false n n Test condition, follow path if structure n Single-entry/single-exit 146

2 if/else Selection Structure n if n n if/else n n Performs action if condition true Different actions if conditions true or false Pseudocode if student’s grade is greater than or equal to 60 print “Passed” else print “Failed” n C code if ( grade >= 60 ) printf(“passed”); else printf(“failed”); 147

if/else Selection Structure n Nested if/else structures n n One inside another, test for multiple cases Once condition met, other statements skipped if student’s grade is greater than or equal to 90 Print “A” else if student’s grade is greater than or equal to 80 Print “B” else if student’s grade is greater than or equal to 70 Print “C” else if student’s grade is greater than or equal to 60 Print “D” else Print “F” 149

if/else Selection Structure n Example if ( grade >= 90 ) printf("A“); else if ( grade >= 80 ) printf("B”); else if ( grade >= 70 ) printf("C“); else if ( grade >= 60 ) printf("D“); else printf("F“); // 90 and above // 80 -89 // 70 -79 // 60 -69 // less than 60 150

if/else Selection Structure n Compound statement n Set of statements within a pair of braces if ( grade >= 60 ) printf ("Passed. n“); else { printf ("Failed”)n"; printf (“You must take this course again. n“); } n Without braces, Printf("You must take this course again. n“); always executed n Block n Set of statements within braces 151

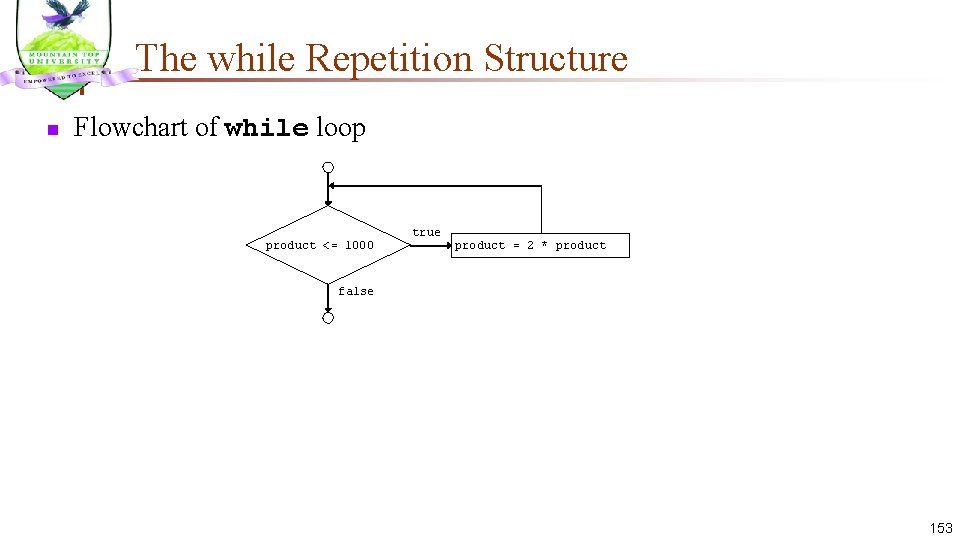
while Repetition Structure n Repetition structure n n Action repeated while some condition remains true Psuedocode while there are more items on my shopping list Purchase next item and cross it off my list n n while loop repeated until condition becomes false Example int product = 2; while ( product <= 1000 ) product = 2 * product; 152

The while Repetition Structure n Flowchart of while loop product <= 1000 true product = 2 * product false 153

Formulating Algorithms (Counter-Controlled Repetition) n Counter-controlled repetition n n Definite repetition n n Loop repeated until counter reaches certain value Number of repetitions known Example A class of ten students took a quiz. The grades (integers in the range 0 to 100) for this quiz are available to you. Determine the class average on the quiz. 154

Formulating Algorithms (Counter-Controlled Repetition) n Pseudocode for example: Set total to zero Set grade counter to one While grade counter is less than or equal to ten Input the next grade Add the grade into the total Add one to the grade counter Set the class average to the total divided by ten Print the class average n Next: C code for this example 155

n n n n // Class average program with counter-controlled repetition. #include <stdio. h> #include <stdlib. h> // function main begins program execution int main() { int total; // sum of grades input by user int grade. Counter; // number of grade to be entered next int grade; // grade value int average; // average of grades // initialization phase total = 0; // initialize total grade. Counter = 1; // initialize loop counter 156

References n n Paul Deitel and Harvey Deitel, C How to Program, 7/e. SBN-10: 0 -13299044 -X ISBN-13: 978 -0 -13 -299044 -8 Introduction to Algorithms, by Thomas H. Cormen Charles E. Leiserson, Ronald L. Rivest Clifford Stein Publisher: The MIT Press; 3 rd edition (July 31, 2009) ISBN-10: 0262033844 n Falana O. J. by Introduction to Algorithm Development is licensed under a Creative Commons Attribution-Non Commercial 4. 0 International License 157