Aljabar Boolean Rinaldi MunirIF 2151 Mat Diskrit 1

Aljabar Boolean Rinaldi Munir/IF 2151 Mat. Diskrit 1

Definisi Aljabar Boolean Rinaldi Munir/IF 2151 Mat. Diskrit 2

Rinaldi Munir/IF 2151 Mat. Diskrit 3

Untuk mempunyai sebuah aljabar Boolean, harus diperlihatkan: 1. Elemen-elemen himpunan B, 2. Kaidah operasi untuk operator biner dan operator uner, 3. Memenuhi postulat Huntington. Rinaldi Munir/IF 2151 Mat. Diskrit 4

Aljabar Boolean Dua-Nilai Rinaldi Munir/IF 2151 Mat. Diskrit 5

Rinaldi Munir/IF 2151 Mat. Diskrit 6

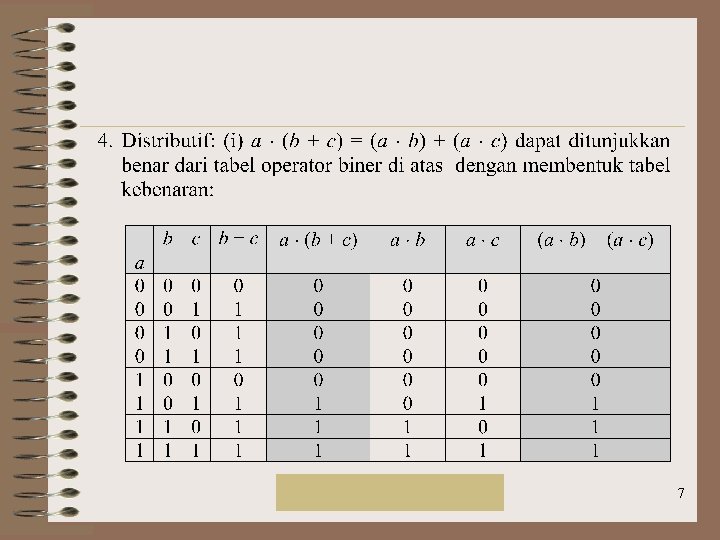
Rinaldi Munir/IF 2151 Mat. Diskrit 7

Rinaldi Munir/IF 2151 Mat. Diskrit 8

Ekspresi Boolean Rinaldi Munir/IF 2151 Mat. Diskrit 9

Mengevaluasi Ekspresi Boolean Rinaldi Munir/IF 2151 Mat. Diskrit 10

Rinaldi Munir/IF 2151 Mat. Diskrit 11

Prinsip Dualitas Rinaldi Munir/IF 2151 Mat. Diskrit 12

Hukum-hukum Aljabar Boolean Rinaldi Munir/IF 2151 Mat. Diskrit 13

Rinaldi Munir/IF 2151 Mat. Diskrit 14

Fungsi Boolean Rinaldi Munir/IF 2151 Mat. Diskrit 15

Rinaldi Munir/IF 2151 Mat. Diskrit 16

Rinaldi Munir/IF 2151 Mat. Diskrit 17

Rinaldi Munir/IF 2151 Mat. Diskrit 18

Komplemen Fungsi Rinaldi Munir/IF 2151 Mat. Diskrit 19

Rinaldi Munir/IF 2151 Mat. Diskrit 20

Bentuk Kanonik Rinaldi Munir/IF 2151 Mat. Diskrit 21

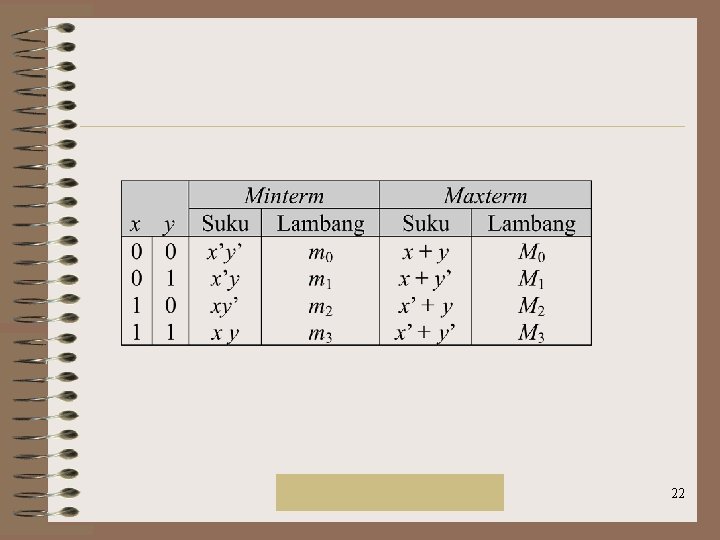
Rinaldi Munir/IF 2151 Mat. Diskrit 22

Rinaldi Munir/IF 2151 Mat. Diskrit 23

Rinaldi Munir/IF 2151 Mat. Diskrit 24

Rinaldi Munir/IF 2151 Mat. Diskrit 25

Rinaldi Munir/IF 2151 Mat. Diskrit 26

Rinaldi Munir/IF 2151 Mat. Diskrit 27

Rinaldi Munir/IF 2151 Mat. Diskrit 28

Konversi Antar Bentuk Kanonik Rinaldi Munir/IF 2151 Mat. Diskrit 29

Rinaldi Munir/IF 2151 Mat. Diskrit 30

Rinaldi Munir/IF 2151 Mat. Diskrit 31

Bentuk Baku • Tidak harus mengandung literal yang lengkap. • Contohnya, f(x, y, z) = y’ + xy + x’yz (bentuk baku SOP f(x, y, z) = x(y’ + z)(x’ + y + z’) (bentuk baku POS) Rinaldi Munir/IF 2151 Mat. Diskrit 32

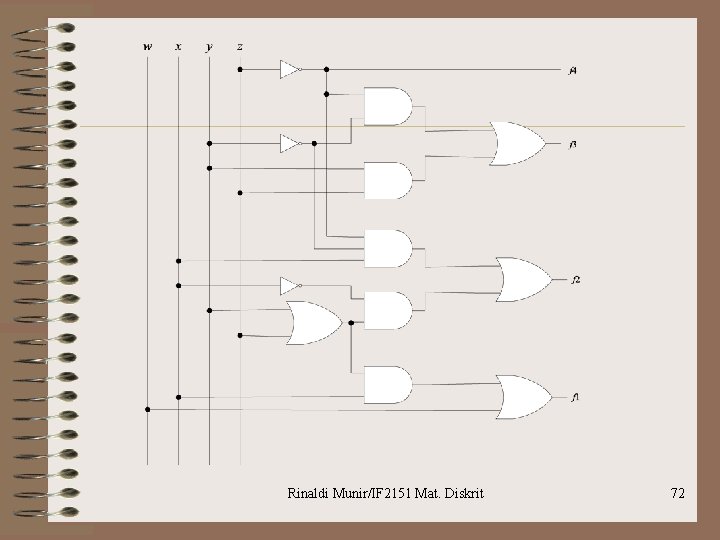
Aplikasi Aljabar Boolean Rinaldi Munir/IF 2151 Mat. Diskrit 33

Rinaldi Munir/IF 2151 Mat. Diskrit 34

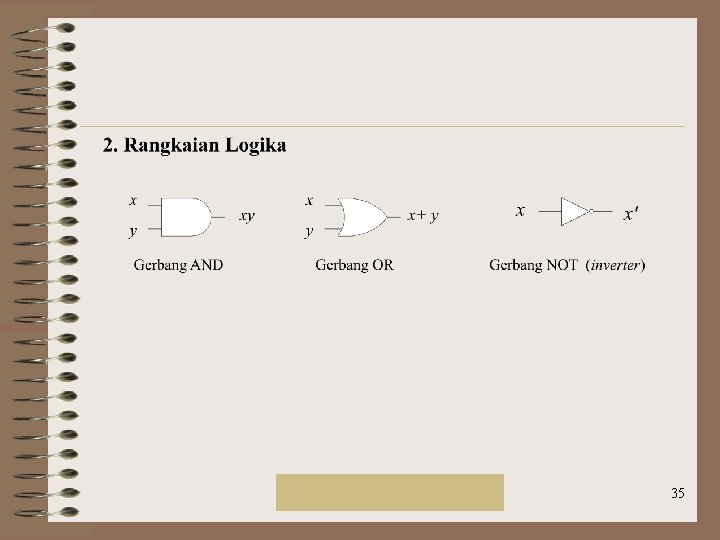
Rinaldi Munir/IF 2151 Mat. Diskrit 35

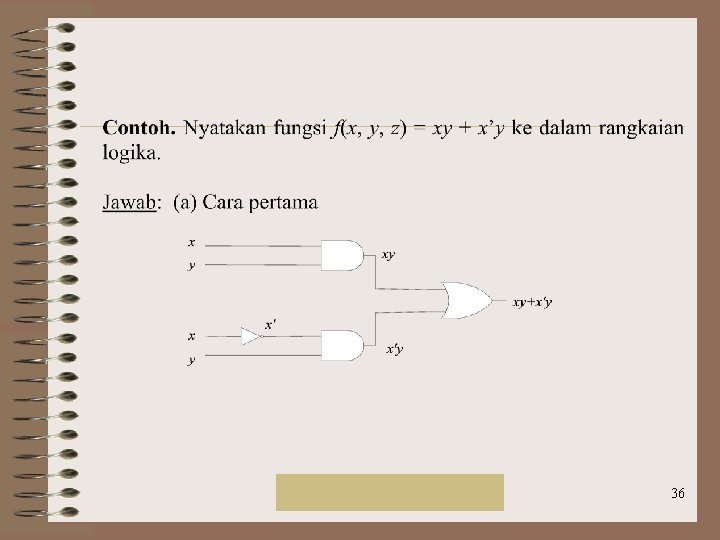
Rinaldi Munir/IF 2151 Mat. Diskrit 36

Rinaldi Munir/IF 2151 Mat. Diskrit 37

Rinaldi Munir/IF 2151 Mat. Diskrit 38

Rinaldi Munir/IF 2151 Mat. Diskrit 39

Penyederhanaan Fungsi Boolean Rinaldi Munir/IF 2151 Mat. Diskrit 40

1. Penyederhanaan Secara Aljabar Rinaldi Munir/IF 2151 Mat. Diskrit 41

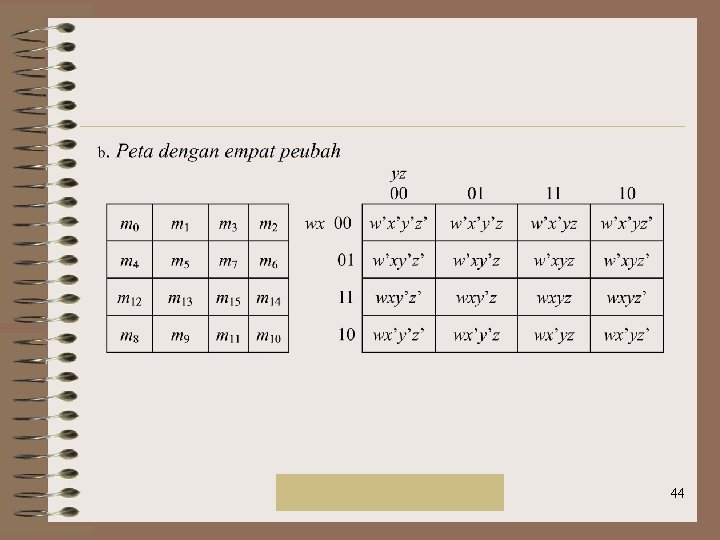
2. Peta Karnaugh Rinaldi Munir/IF 2151 Mat. Diskrit 42

Rinaldi Munir/IF 2151 Mat. Diskrit 43

Rinaldi Munir/IF 2151 Mat. Diskrit 44

Rinaldi Munir/IF 2151 Mat. Diskrit 45

Rinaldi Munir/IF 2151 Mat. Diskrit 46

Rinaldi Munir/IF 2151 Mat. Diskrit 47

Rinaldi Munir/IF 2151 Mat. Diskrit 48

Rinaldi Munir/IF 2151 Mat. Diskrit 49

Rinaldi Munir/IF 2151 Mat. Diskrit 50

Rinaldi Munir/IF 2151 Mat. Diskrit 51

Rinaldi Munir/IF 2151 Mat. Diskrit 52

Rinaldi Munir/IF 2151 Mat. Diskrit 53

Rinaldi Munir/IF 2151 Mat. Diskrit 54

Rinaldi Munir/IF 2151 Mat. Diskrit 55

Rinaldi Munir/IF 2151 Mat. Diskrit 56

Rinaldi Munir/IF 2151 Mat. Diskrit 57

Rinaldi Munir/IF 2151 Mat. Diskrit 58

Rinaldi Munir/IF 2151 Mat. Diskrit 59

Rinaldi Munir/IF 2151 Mat. Diskrit 60

Rinaldi Munir/IF 2151 Mat. Diskrit 61

Rinaldi Munir/IF 2151 Mat. Diskrit 62

Rinaldi Munir/IF 2151 Mat. Diskrit 63

Kondisi Don’t care Rinaldi Munir/IF 2151 Mat. Diskrit 64

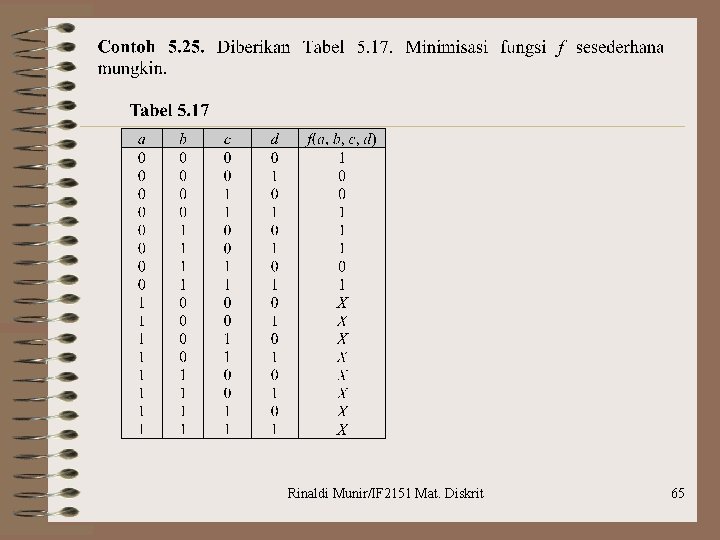
Rinaldi Munir/IF 2151 Mat. Diskrit 65

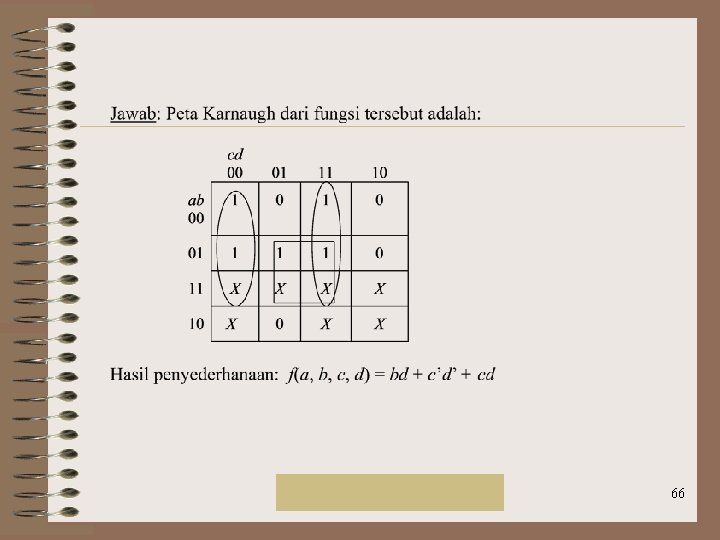
Rinaldi Munir/IF 2151 Mat. Diskrit 66

Rinaldi Munir/IF 2151 Mat. Diskrit 67

Rinaldi Munir/IF 2151 Mat. Diskrit 68

Rinaldi Munir/IF 2151 Mat. Diskrit 69

Rinaldi Munir/IF 2151 Mat. Diskrit 70

Rinaldi Munir/IF 2151 Mat. Diskrit 71

Rinaldi Munir/IF 2151 Mat. Diskrit 72

Rinaldi Munir/IF 2151 Mat. Diskrit 73

Rinaldi Munir/IF 2151 Mat. Diskrit 74

Metode Quine-Mc. Cluskey • Metode Peat Karnaugh tidak mangkus untuk jumlah peubah > 6 (ukuran peta semakin besar). • Metode peta Karnaugh lebih sulit diprogram dengan komputer karena diperlukan pengamatan visual untuk mengidentifikasi minterm-minterm yang akan dikelompokkan. • Metode alternatif adalah metode Quine. Mc. Cluskey. Metode ini mudah diprogram. Rinaldi Munir/IF 2151 Mat. Diskrit 75

Rinaldi Munir/IF 2151 Mat. Diskrit 76

Rinaldi Munir/IF 2151 Mat. Diskrit 77

Rinaldi Munir/IF 2151 Mat. Diskrit 78

Rinaldi Munir/IF 2151 Mat. Diskrit 79

Rinaldi Munir/IF 2151 Mat. Diskrit 80

Latihan soal 1. Implementasikan fungsi f(x, y, z) = (0, 6) dan hanya dengan gerbang NAND saja. 2. Gunakan Peta Karnaugh untuk merancang rangkaian logika yang dapat menentukan apakah sebuah angka desimal yang direpresentasikan dalam bit biner merupakan bilangan genap atau bukan (yaitu, memberikan nilai 1 jika genap dan 0 jika tidak). Rinaldi Munir/IF 2151 Mat. Diskrit 81

3. Sebuah instruksi dalam sebuah program adalah if A > B then writeln(A) else writeln(B); Nilai A dan B yang dibandingkan masing-masing panjangnya dua bit (misalkan a 1 a 2 dan b 1 b 2). (a) Buatlah rangkaian logika (yang sudah disederhanakan tentunya) yang menghasilkan keluaran 1 jika A > B atau 0 jika tidak. (b) Gambarkan kembali rangkaian logikanya jika hanya menggunakan gerbang NAND saja (petunjuk: gunakan hukum de Morgan) Rinaldi Munir/IF 2151 Mat. Diskrit 82

5. Buatlah rangkaian logika yang menerima masukan dua-bit dan menghasilkan keluaran berupa kudrat dari masukan. Sebagai contoh, jika masukannya 11 (3 dalam sistem desimal), maka keluarannya adalah 1001 (9 dalam sistem desimal). Rinaldi Munir/IF 2151 Mat. Diskrit 83