MATEMATIKA DISKRIT TEAM TEACHING MATEMATIKA DISKRIT MATEMATIKA DISKRIT

MATEMATIKA DISKRIT TEAM TEACHING MATEMATIKA DISKRIT

MATEMATIKA DISKRIT 3 SKS p Buku Teks : Discrete Mathematics and Its Applications, Kenneth H Rossen, Mc. Graw-Hill p Penilaian : n n Tugas Kuis UTS UAS

LOGIKA DAN EKUIVALENSI LOGIKA Bab 1 Sub-bab 1. 1 – 1. 2

Tujuan Instruksional khusus Memahami tentang logika proposional p Memahami tentang penggunaan operator logika pada proposisi p Memahami tentang ekuivalensi pada logika proposional p

Logika p p Logika adalah dasar dari penjabaran matematika (mathematical reasoning) Logika mempelajari penjabaran (reasoning) secara benar Fokus pada relasi antar pernyataan (statement) / kalimat (sentence). Contoh: Dino adalah mahasiswa UB. Semua mahasiswa UB pandai. Dino orang pandai. Perhatikan bahwa logika tidak harus memperhatikan isi kalimat; jika diketahui bahwa dua kalimat pertama di atas benar, maka kalimat ketiga harus benar.

Proposisi p p Proposisi merupakan sebuah pernyataan atau kalimat yang punya nilai kebenaran (benar = 1 / salah = 0). Proposisi disimbolkan dengan huruf p, q, dsb. Biasanya berbentuk kalimat deklaratif Contoh bukan proposisi: n Berapa harga tiket ke Malaysia? n Silakan duduk.

MACAM PROPOSISI p p Kalimat deklaratif yang tidak memuat penghubung disebut proposisi (primitif ) ex: n 2 adalah Bilangan bulat Kalimat deklaratif yg memuat penghubung ”atau” “dan” ”jika maka” disebut proposisi majemuk (compound) ex: n Taufik Hidayat pandai main bulu tangkis atau tenis

Konektif Jika p dan q adalah proposisi, dapat dibentuk proposisi (majemuk) baru (compound proposition) dengan menggunakan konektif p Macam-macam konektif: p n n n NOT (negasi) AND (konjungsi) Inclusive OR (disjungsi) Exclusive OR Implikasi ganda Simbol Simbol atau ‾ ^ v

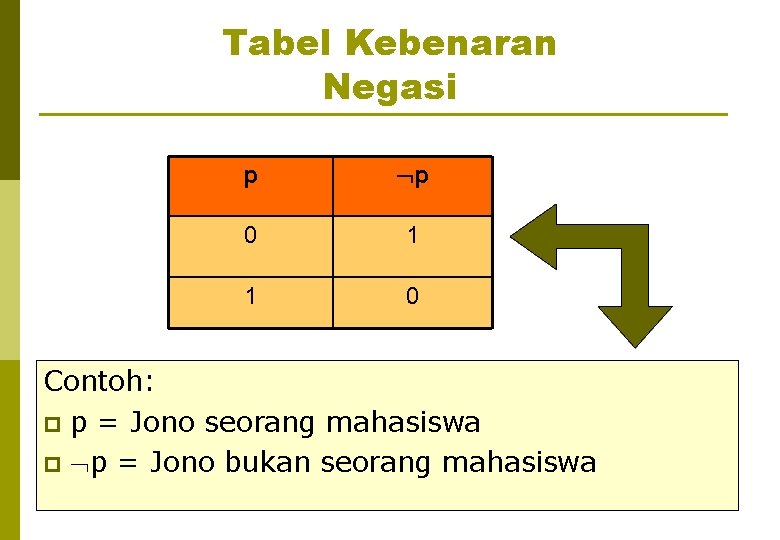
Tabel Kebenaran Negasi p p 0 1 1 0 Contoh: p p = Jono seorang mahasiswa p p = Jono bukan seorang mahasiswa

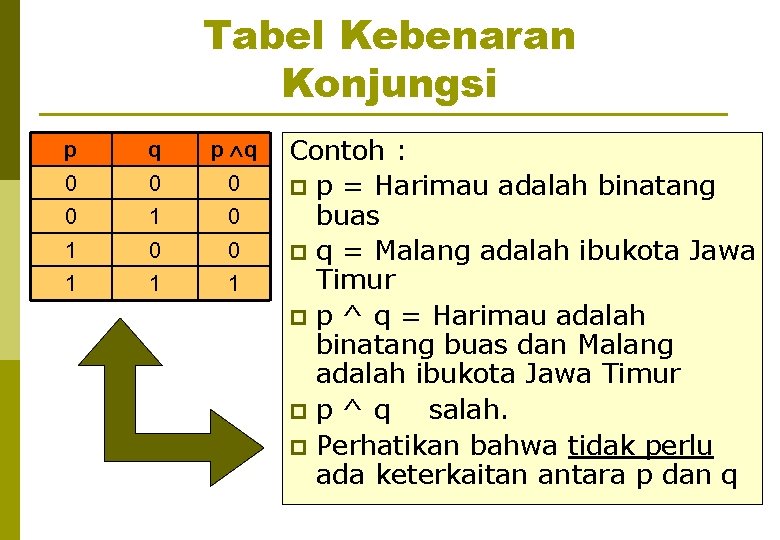
Tabel Kebenaran Konjungsi p q 0 0 1 1 1 Contoh : p p = Harimau adalah binatang buas p q = Malang adalah ibukota Jawa Timur p p ^ q = Harimau adalah binatang buas dan Malang adalah ibukota Jawa Timur p p ^ q salah. p Perhatikan bahwa tidak perlu ada keterkaitan antara p dan q

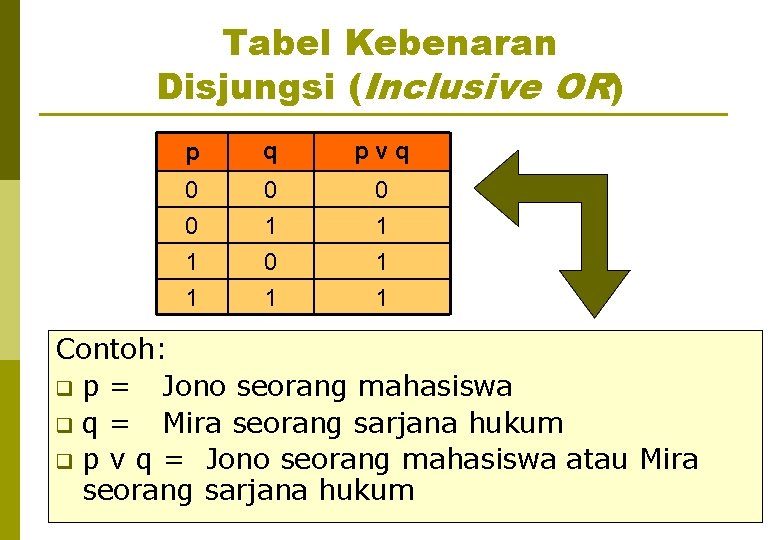
Tabel Kebenaran Disjungsi (Inclusive OR) p q pvq 0 0 1 1 0 1 0 1 1 1 Contoh: q p = Jono seorang mahasiswa q q = Mira seorang sarjana hukum q p v q = Jono seorang mahasiswa atau Mira seorang sarjana hukum

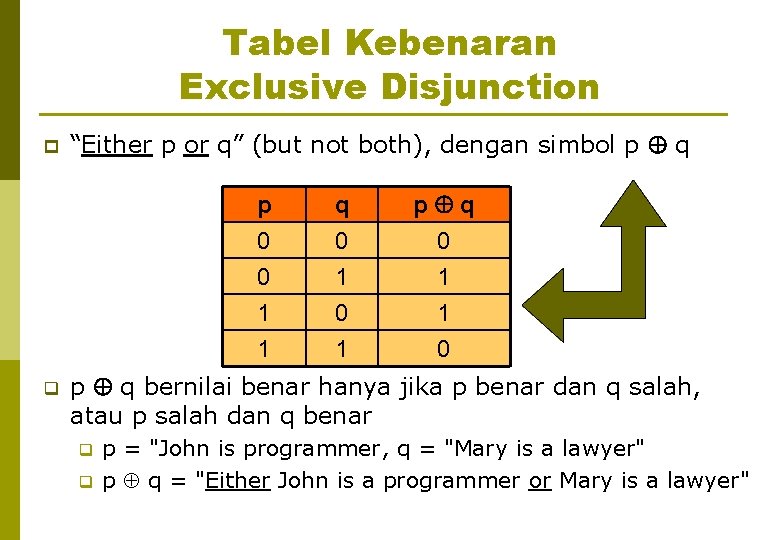
Tabel Kebenaran Exclusive Disjunction p q “Either p or q” (but not both), dengan simbol p q p 0 0 1 q 0 1 0 p q 0 1 1 0 p q bernilai benar hanya jika p benar dan q salah, atau p salah dan q benar q q p = "John is programmer, q = "Mary is a lawyer" p q = "Either John is a programmer or Mary is a lawyer"

Kalimat majemuk (compound statements) p p, q, r merupakan kalimat / pernyataan sederhana (simple statements) Apabila ada dua buah proposisi misalkan proposisi A dan proposisi B maka dapat dibentuk proposisi baru (Compound Proposition) dengan menggunakan konektor atau perangkai. Beberapa contoh bentukan compound statements, seperti: n (p q)^r n p (q^r) n ( p) ( q) n (p q)^( r) n dll

Tingkat Presedensi p Urutan penyelesaian logika jika menemui proposisi majemuk

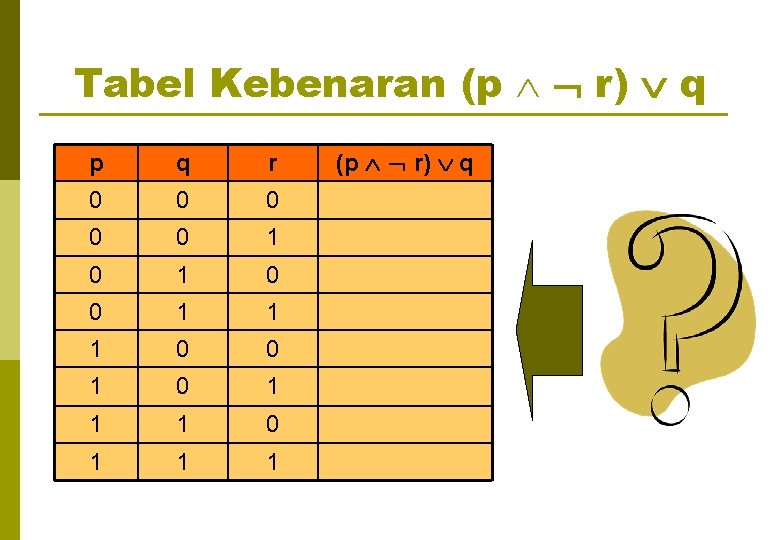
Tabel Kebenaran (p r) q p q r 0 0 0 1 1 1 0 0 1 1 1 (p r) q

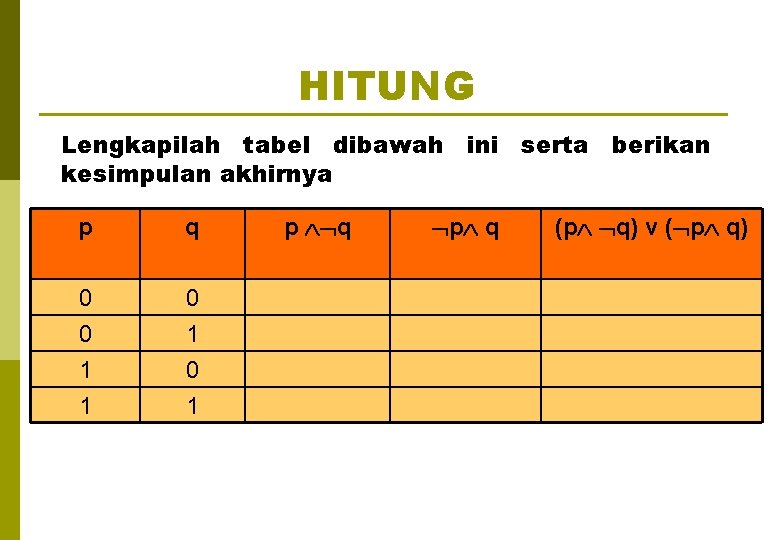
HITUNG Lengkapilah tabel dibawah ini serta berikan kesimpulan akhirnya p q 0 0 0 1 1 1 0 1 p q p q (p q) v ( p q)

Implikasi Disebut juga proposisi kondisional (conditional proposition) dan berbentuk “jika p maka q” p Notasi simboliknya : p q p Contoh: p = Jono seorang mahasiswa q = Mira seorang sarjana hukum p q = Jika Jono seorang mahasiswa maka Mira seorang sarjana hukum

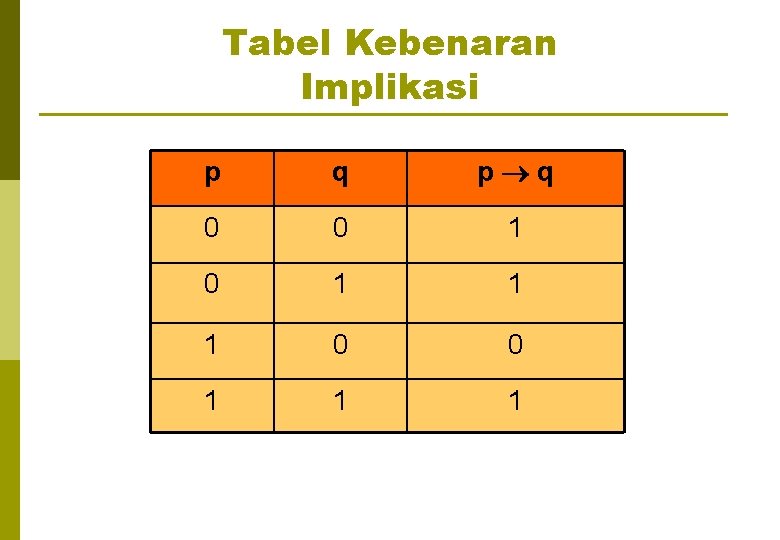
Tabel Kebenaran Implikasi p q 0 0 1 1 1

Hypotesa dan konklusi p Dalam implikasi p q p disebut antecedent, hypothesis, premise q disebut konsekuensi atau konklusi (consequent, conclusion)

Perlu dan Cukup Kondisi “perlu” dinyatakan oleh konklusi. p Kondisi “cukup” dinyatakan oleh hipotesa. p Perlu = necessary; Cukup = sufficient p n n n Contoh: p Jika Jono seorang mahasiswa maka Mira seorang sarjana hukum Kondisi perlu: Mira seorang sarjana hukum Kondisi cukup: Jono seorang mahasiswa

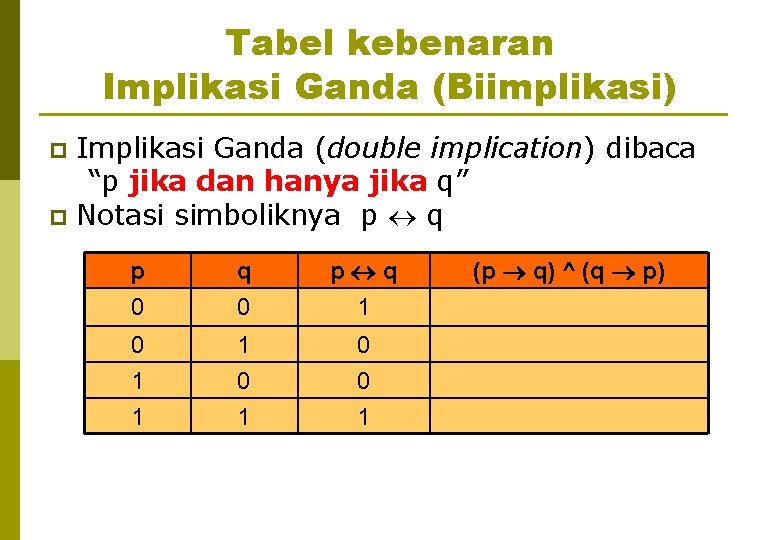
Tabel kebenaran Implikasi Ganda (Biimplikasi) Implikasi Ganda (double implication) dibaca “p jika dan hanya jika q” p Notasi simboliknya p q p p 0 q 0 p q 1 0 1 1 0 0 0 1 1 1 (p q) ^ (q p)

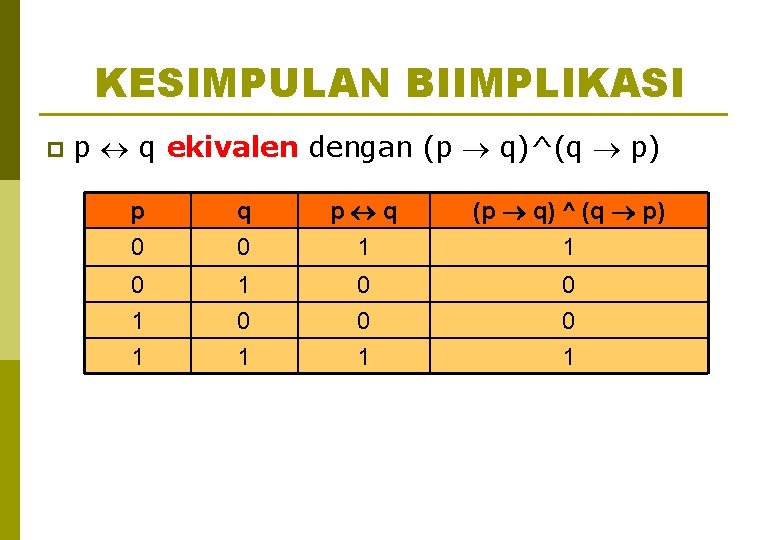
KESIMPULAN BIIMPLIKASI p p q ekivalen dengan (p q)^(q p) p 0 q 0 p q 1 (p q) ^ (q p) 1 0 1 1 0 0 0 1 1

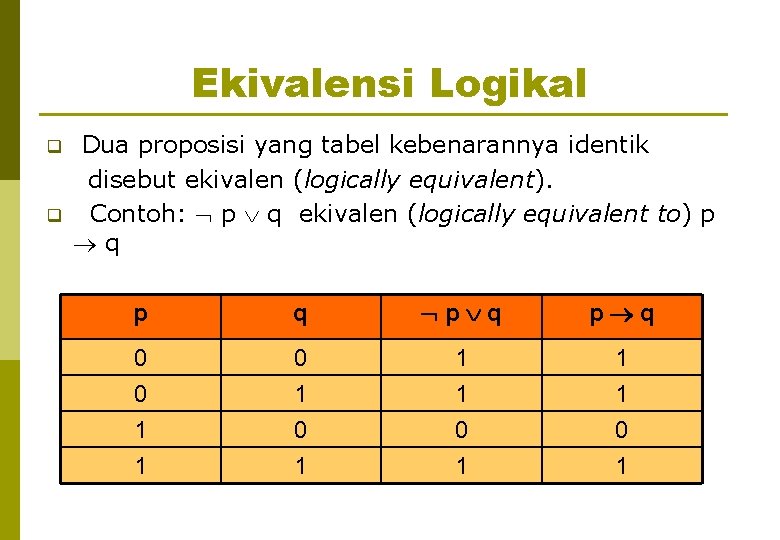
Ekivalensi Logikal q q Dua proposisi yang tabel kebenarannya identik disebut ekivalen (logically equivalent). Contoh: p q ekivalen (logically equivalent to) p q p q 0 0 1 0 1 1

Konversi dan Inversi p p p Konversi dari p q adalah q p Inversi dari p q adalah p q Apakah Konversi dan Inversi diatas equivalent? ? ? BUKTIKAN!!!!

Kontrapositif kontrapositif dari proposisi p q adalah q p p Buat Tabel Kebenarannya dan apakah p q dan q p ekivalen? ? ? p

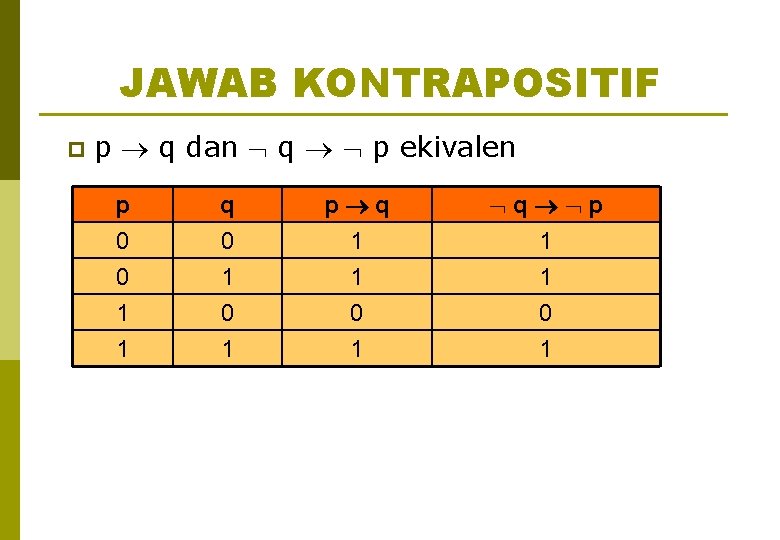
JAWAB KONTRAPOSITIF p p q dan q p ekivalen p 0 0 1 q 0 1 0 p q 1 1 0 q p 1 1 0 1 1

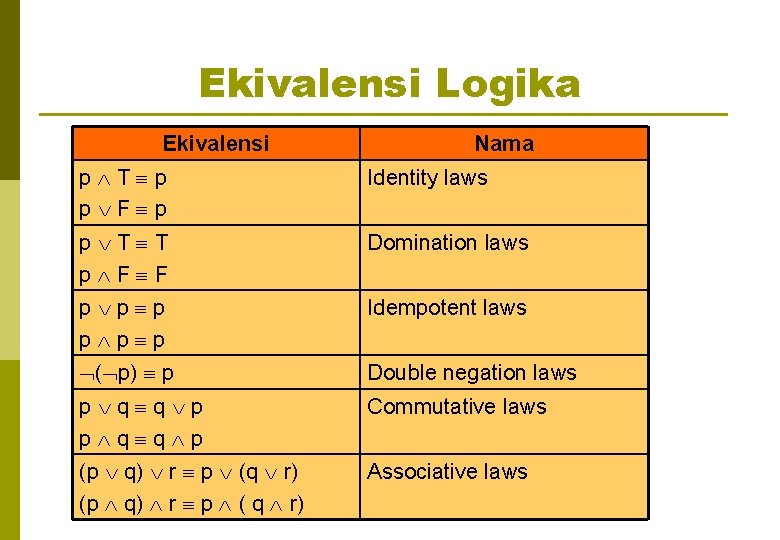
Ekivalensi Logika Ekivalensi Nama p T p p F p Identity laws p T T p F F Domination laws p p p Idempotent laws ( p) p Double negation laws p q q p Commutative laws (p q) r p (q r) (p q) r p ( q r) Associative laws

Ekivalensi Logika Ekivalensi Nama p (q r) (p q) (p r) Distributive laws (p q) ( p) ( q) De Morgan’s laws p (p q) p Absorption laws p p T p p F Negation laws

Ekivalensi Logika Ekivalensi p q q p p q (p q) p q (p q) (p r) p (q r) (p r) (q r) (p q) r (p q) (p r) p (q r) (p r) (q r) (p q) r Ekivalensi p q (p q) (q p) p q (p q) ( p q) (p q) p q

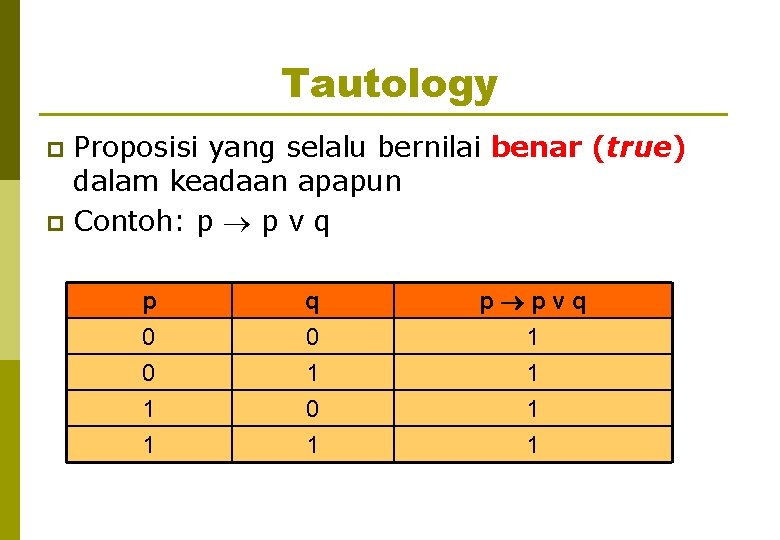
Tautology Proposisi yang selalu bernilai benar (true) dalam keadaan apapun p Contoh: p p v q p p 0 0 1 q 0 1 0 p pvq 1 1 1

Kontradiksi p Proposisi yang selalu bernilai salah (false) dalam keadaan apapun p Contoh : p ^ p p p ^ ( p) 0 0 1 0

Latihan-1 1. Dari bbrp kalimat dibawah ini mana yang termasuk proposisi ? Tentukan nilai kebenaran dari proposisi tsb. p p p 7 merupakan sebuah bilangan prima. Jangan lakukan. Jika 10 habis dibagi dengan 4, maka juga habis dibagi dengan 2. x + y = y + x untuk setiap pasangan dari bilangan real x dan y Jam berapa sekarang?

Latihan 2. Tentukan apakah ( p (p q)) q adalah tautologi? 3. Tunjukkan bahwa manakah yang ekivalen dari ketiga logika berikut? a. p q b. (p q) ( p q) c. (p q) ^ (q p)