POHON TREE Matematika Diskrit Definisi Pohon tree adalah

POHON (TREE) Matematika Diskrit

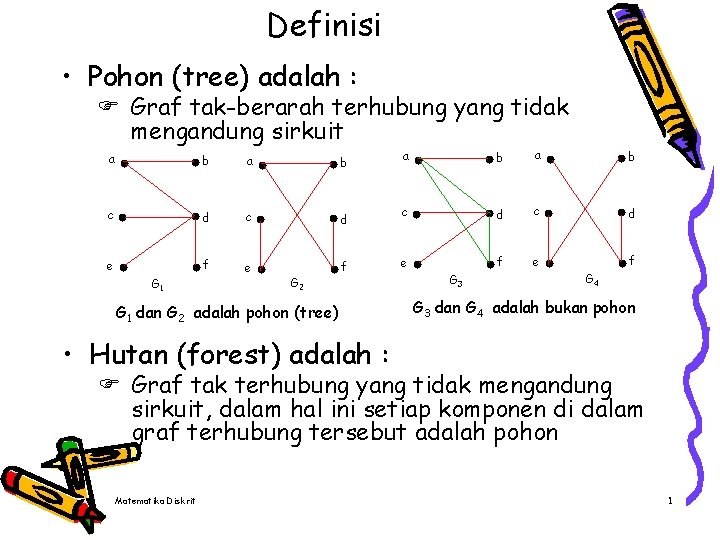
Definisi • Pohon (tree) adalah : F Graf tak-berarah terhubung yang tidak mengandung sirkuit a b c d e f G 1 G 2 G 1 dan G 2 adalah pohon (tree) a b c d e f G 3 G 4 G 3 dan G 4 adalah bukan pohon • Hutan (forest) adalah : F Graf tak terhubung yang tidak mengandung sirkuit, dalam hal ini setiap komponen di dalam graf terhubung tersebut adalah pohon Matematika Diskrit 1

Sifat-sifat Pohon Misalkan G = (V, E) adalah graf tak-berarah sederhana dan jumlah simpulnya n, maka : 1. 2. 3. 4. 5. 6. G adalah pohon Setiap pasang simpul di dalam G terhubung dengan lintasan tunggal G terhubung dan memiliki m = n -1 buah sisi G tidak mengandung sirkuit dan memiliki m = n – 1 buah sisi G tidak mengandung sirkuit dan penambahan satu sisi pada graf akan membuat hanya satu sirkuit G terhubung dan semua sisinya adalah jembatan (jembatan adalah sisi yang bila dihapus menyebabkan graf terpecah menjadi dua komponen) Jika hutan F dengan k komponen mempunyai m = n – 1 buah sisi Matematika Diskrit 2

Contoh Sebuah pohon mempunyai 2 n buah simpul berderajat 1, 3 n buah simpul berderajat 2 dan n buah simpul berderajat 3. Tentukan banyaknya simpul dan sisi di dalam pohon tersebut ! Penyelesaian : Berdasarkan lemma jabat tangan : jumlah semua simpul di dalam graf adalah 2 kali jumlah sisi di dalam graf tersebut (2 n x 1) + (3 n x 2) + (n x 3) = 2 |E| 11 n = 2 |E| ……………… (1) Jumlah sisi pada sebuah pohon adalah jumlah simpul minus satu, sehingga : |E| = (2 n + 3 n + 1) – 1 = 6 n – 1 ………………… (2) Persamaan (1) dan (2) menjadi : 11 n = 2 (6 n – 1) 11 n = 12 n – 2 n=2 Jadi : Ä Jumlah simpul pada pohon 6 n = 6 x 2 = 12 buah simpul Ä Jumlah sisi 6 n – 1 = 11 buah sisi Matematika Diskrit 3

Pohon Merentang (Spanning Tree) • Pohon merentang adalah : F Subgraf dari graf terhubung berbentuk pohon T 2 T 3 T 4 T 1 G Graf lengkap G dengan 4 buah pohon merentangnya, T 1, T 2, T 3 dan T 4 • • Setiap graf terhubung mempunyai paling sedikit 1 buah pohon merentang Cabang (branch) adalah : F Sisi dari graf semula (sisi pada pohon merentang) • Tali-hubung (chord atau link) dari pohon adalah : F Sisi dari graf yang tidak terdapat di dalam pohon merentang • Komplemen pohon adalah : F Himpunan tali-hubung beserta simpul yang bersisian dengannya Matematika Diskrit 4

Pohon Merentang (Spanning Tree) • Jika n buah simpul dan m buah sisi maka : F Untuk graf terhubung : Ä Jumlah cabang : n – 1 Ä Jumlah tali hubung : m – n + 1 F Untuk graf tak-terhubung dengan k komponen : Ä Jumlah cabang : n – k Ä Jumlah tali-hubung : m – n + k • Rank graf G adalah : F Jumlah cabang pada pohon merentang dari sebuah graf G • Nullity graf G adalah : F Jumlah tali hubung pada graf G • Sehingga : jumlah sisi graf G = rank + nullity • Nullity graf sering diacu sebagai bilangan siklomatik atau bilangan Betti pertama • Sirkuit fundamental (fundamental circuit) adalah : F Sirkuit yang terbentuk dengan penambahan sebuah tali-hubung pada pohon merentang Matematika Diskrit 5

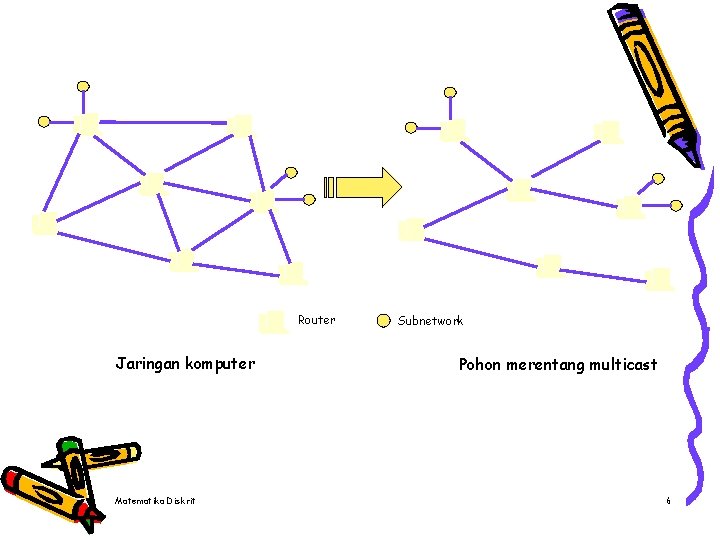
Router Jaringan komputer Matematika Diskrit Subnetwork Pohon merentang multicast 6

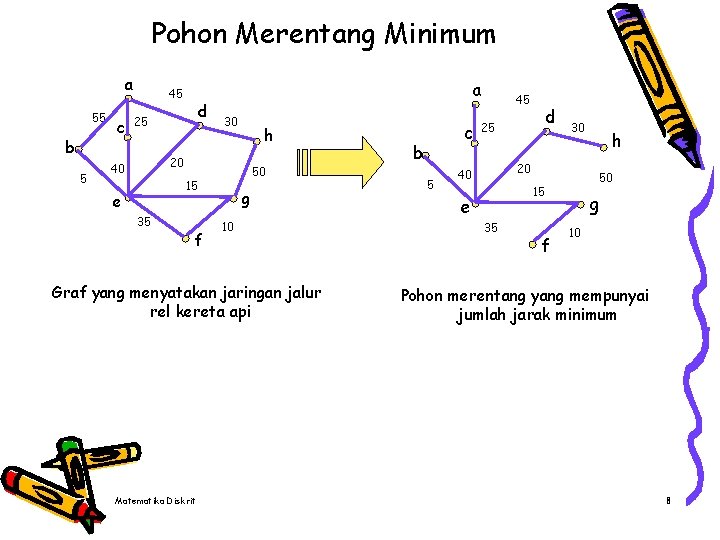
Pohon Merentang Minimum (Minimum Spanning Tree) • Adalah pohon merentang yang berbobot minimum • Aplikasi misalnya pada : Ä Jalur rel kereta api yang menghubungkan sejumlah kota • Algoritma yang digunakan : 1. Algoritma Prim 2. Algoritma Kruskal Matematika Diskrit 7

Pohon Merentang Minimum a 55 b 5 c 45 d 25 a 30 h 20 40 50 15 e 35 f g 10 Graf yang menyatakan jaringan jalur rel kereta api Matematika Diskrit c b 5 45 25 d 30 h 20 40 50 15 e 35 f g 10 Pohon merentang yang mempunyai jumlah jarak minimum 8

Algoritma Prim : • Ambil sisi dari graf G yang berbobot minimum, masukkan ke dalam T • Pilih sisi e yang mempunyai bobot minimum dan bersisian dengan simpul di T, tetapi e tidak membentuk sirkuit di T. Masukkan e ke dalam T • Ulangi langkah-2 sebanyak n – 2 kali Matematika Diskrit 9

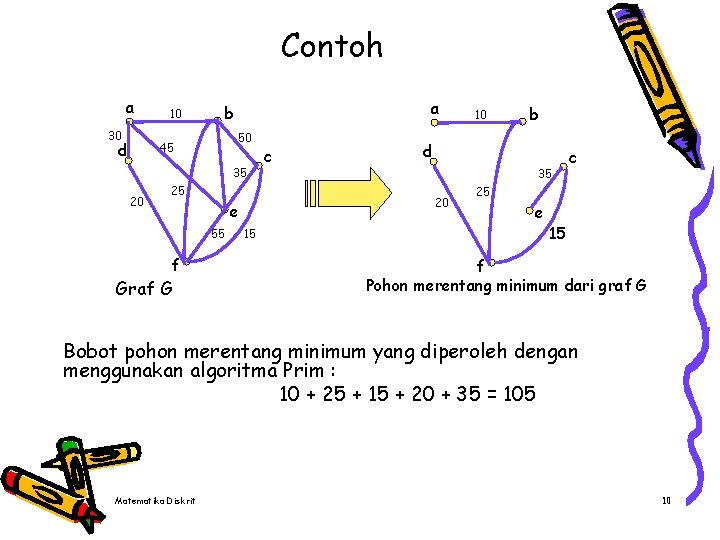
Contoh a 30 d 10 a b 50 45 35 20 25 f Graf G 15 b d 35 20 e 55 c 10 c 25 e 15 f Pohon merentang minimum dari graf G Bobot pohon merentang minimum yang diperoleh dengan menggunakan algoritma Prim : 10 + 25 + 15 + 20 + 35 = 105 Matematika Diskrit 10

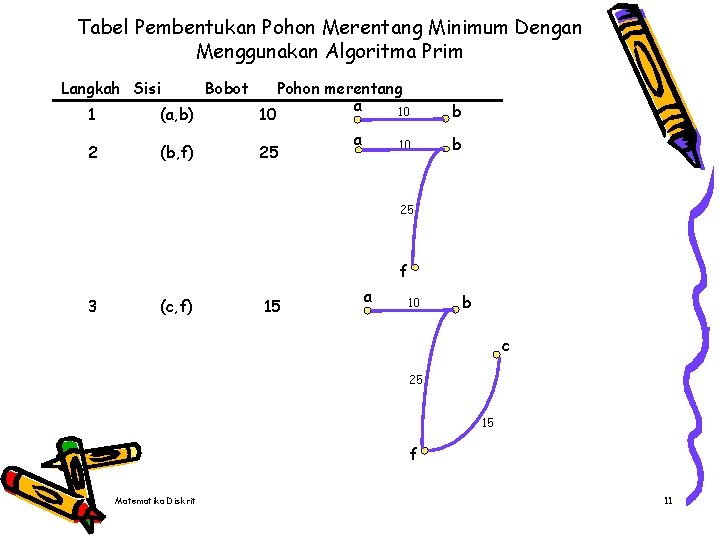
Tabel Pembentukan Pohon Merentang Minimum Dengan Menggunakan Algoritma Prim Langkah Sisi Bobot Pohon merentang a 10 1 (a, b) 10 2 (b, f) 25 a 10 b b 25 f 3 (c, f) 15 a 10 b c 25 15 f Matematika Diskrit 11

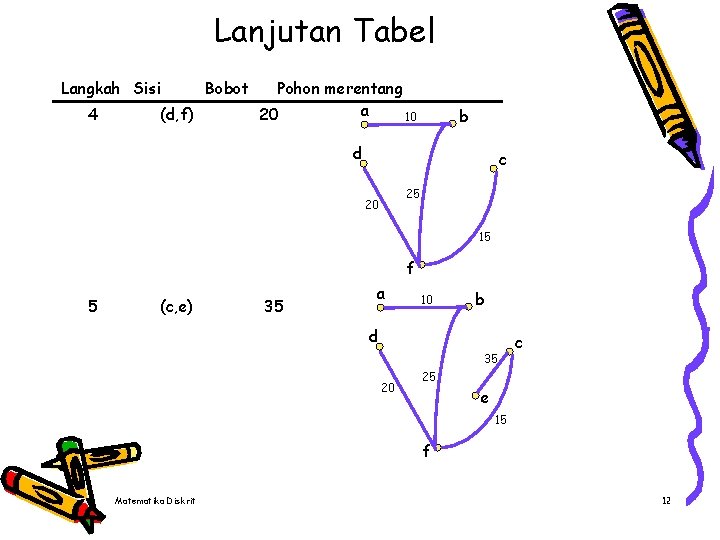
Lanjutan Tabel Langkah Sisi 4 (d, f) Bobot Pohon merentang a 20 10 b d c 25 20 15 f 5 (c, e) 35 a 10 b d 35 20 c 25 e 15 f Matematika Diskrit 12

Algoritma Kruskal : (Asumsi : sisi-sisi dari graf sudah diurut menaik berdasarkan bobotnya) 1. T masih kosong 2. Pilih sisi e yang mempunyai bobot minimum yang tidak membentuk sirkuit di T. Masukkan e ke dalam T 3. Ulangi langkah-2 sebanyak n – 1 kali Matematika Diskrit 13

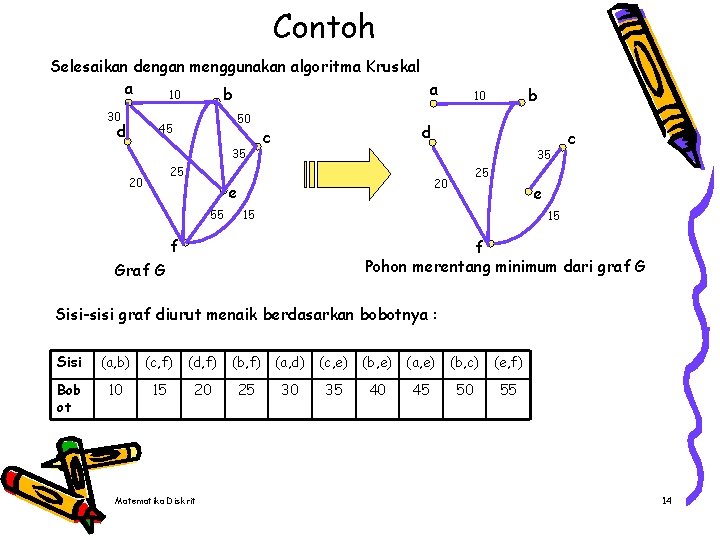
Contoh Selesaikan dengan menggunakan algoritma Kruskal a a 10 b 30 d 50 45 35 d c 35 25 20 c 25 20 e 55 b 10 e 15 15 f f Pohon merentang minimum dari graf G Graf G Sisi-sisi graf diurut menaik berdasarkan bobotnya : Sisi (a, b) (c, f) (d, f) (b, f) (a, d) (c, e) (b, e) (a, e) (b, c) (e, f) Bob ot 10 15 20 25 30 35 40 45 50 55 Matematika Diskrit 14

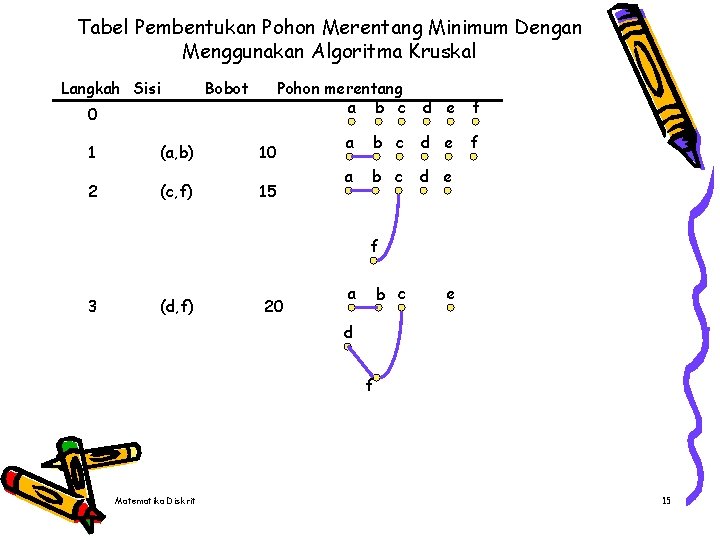
Tabel Pembentukan Pohon Merentang Minimum Dengan Menggunakan Algoritma Kruskal Langkah Sisi Bobot Pohon merentang a b c 0 1 2 (a, b) (c, f) 10 15 d e f f a b c d e f 3 (d, f) 20 a b c e d f Matematika Diskrit 15

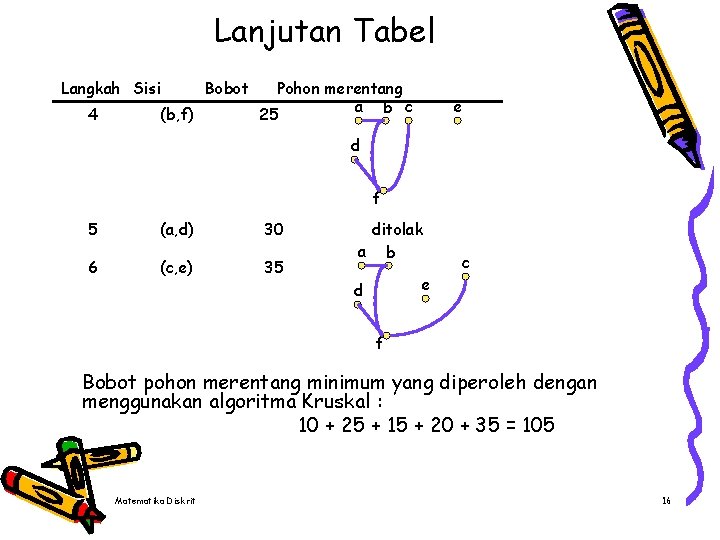
Lanjutan Tabel Langkah Sisi 4 (b, f) Bobot Pohon merentang a b c 25 e d f 5 (a, d) 30 6 (c, e) 35 ditolak a b e d c f Bobot pohon merentang minimum yang diperoleh dengan menggunakan algoritma Kruskal : 10 + 25 + 15 + 20 + 35 = 105 Matematika Diskrit 16

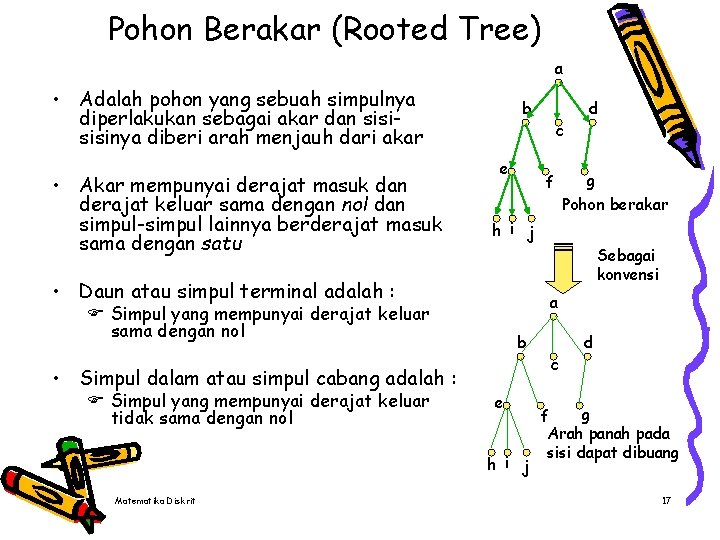
Pohon Berakar (Rooted Tree) a • Adalah pohon yang sebuah simpulnya diperlakukan sebagai akar dan sisinya diberi arah menjauh dari akar • Akar mempunyai derajat masuk dan derajat keluar sama dengan nol dan simpul-simpul lainnya berderajat masuk sama dengan satu b e f Sebagai konvensi a F Simpul yang mempunyai derajat keluar sama dengan nol F Simpul yang mempunyai derajat keluar tidak sama dengan nol b e h i j Matematika Diskrit g Pohon berakar h i j • Daun atau simpul terminal adalah : • Simpul dalam atau simpul cabang adalah : c d g f Arah panah pada sisi dapat dibuang 17

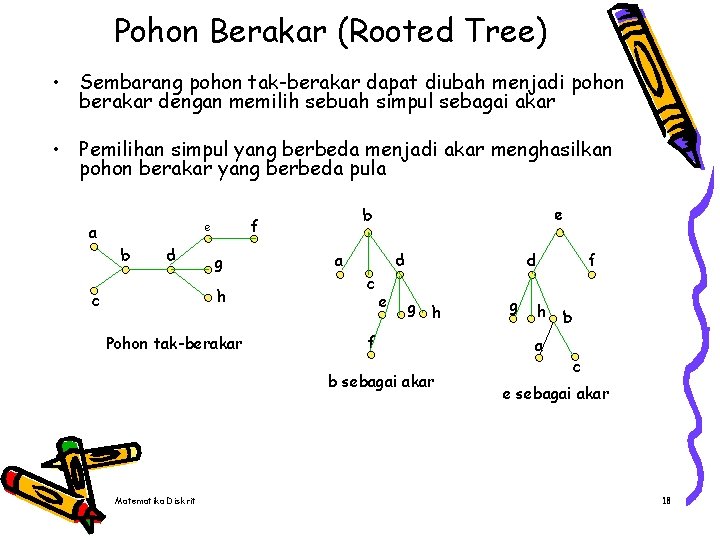
Pohon Berakar (Rooted Tree) • Sembarang pohon tak-berakar dapat diubah menjadi pohon berakar dengan memilih sebuah simpul sebagai akar • Pemilihan simpul yang berbeda menjadi akar menghasilkan pohon berakar yang berbeda pula a b d g h c Pohon tak-berakar e b f e a d d c e g h f b sebagai akar Matematika Diskrit g f h b a c e sebagai akar 18

Terminologi pada Pohon Berakar • • • Child atau children (Anak) dan parent (orangtua) Ä Child dari simpul x jika ada sisi dari simpul x ke y Ä Parent dari simpul y adalah simpul x Ä Pada gambar di samping : Ä Ä Simpul b, c dan d children dari simpul a e dan f children dari simpul b a parent dari simpul b, c dan d b parent dari simpul e dan f Path (lintasan) a b Ä Lintasan dari simpul vi ke simpul vk adalah runtunan simpule simpul v 1, v 2 , …, vk sedemikian hingga vi adalah parent dari vi+1 f untuk 1 i k Ä Panjang lintasan adalah jumlah sisi yang dilalui dalam suatu lintasan, yaitu k – 1. h i j Ä Pada gambar di samping : Ä Lintasan dari a ke j adalah a, b, e dan j Ä Panjang lintasan dari a ke j adalah 3 c d g k l m Descendant (Keturunan) dan ancestor (leluhur) Ä x adalah ancestor dari simpul y jika terdapat lintasan dari simpul x ke simpul y di dalam pohon Ä Descendant dari simpul x adalah simpul y Ä Pada gambar di samping : Ä Simpul b adalah ancestor dari simpul h Ä Simpul h adalah descendant dari simpul b Matematika Diskrit 19

Terminologi pada Pohon Berakar • • • Sibling (saudara kandung) Ä Sibling satu sama lain adalah simpul yang mempunyai parent sama Ä Pada gambar di samping : a Ä Simpul f sibling dari e Ä Simpul g bukan sibling dari e karena parent berbeda b Subtree (subpohon) Ä Subtree dengan x sebagai akarnya adalah subgraf T’ = (V’, E’) sedemikian hingga V’ mengandung x dan semua keturunannya; E’ mengandung sisi-sisi dalam semua lintasan yang berasal dari x Ä Pada gambar di samping : Ä V’ = {b, e, f, h, i, j} Ä E’ = {(b, e), (b, f), (e, h), (e, i), (e, j)} Ä b : simpul akar Degree (derajat) d c e h i g f k j l m Ä Derajat sebuah simpul pohon berakar adalah jumlah subtree (jumlah child) pada simpul tersebut Ä Derajat pohon berakar merupakan derajat keluar Ä Pada gambar di samping : Ä Derajat simpul a : 3, simpul b : 2, simpul c : 0 dan simpul d : 1 Ä Derajat tertinggi (maksimum) : 3 Matematika Diskrit 20

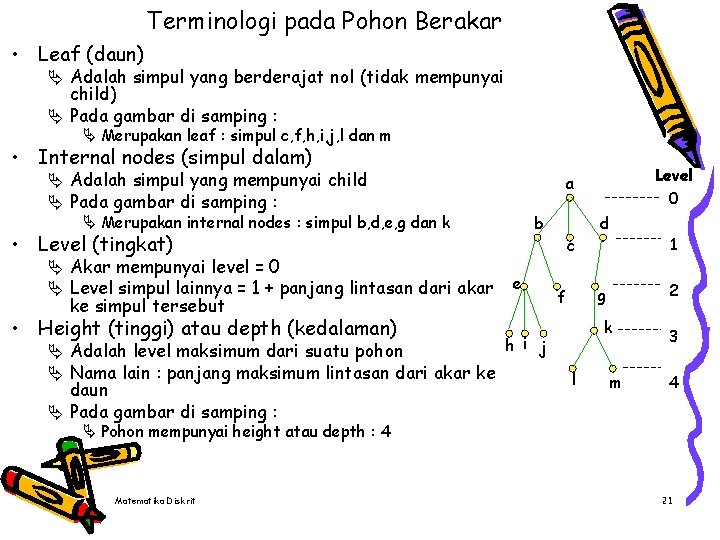
Terminologi pada Pohon Berakar • Leaf (daun) Ä Adalah simpul yang berderajat nol (tidak mempunyai child) Ä Pada gambar di samping : Ä Merupakan leaf : simpul c, f, h, i, j, l dan m • Internal nodes (simpul dalam) Ä Adalah simpul yang mempunyai child Ä Pada gambar di samping : Ä Merupakan internal nodes : simpul b, d, e, g dan k b • Level (tingkat) Ä Akar mempunyai level = 0 Ä Level simpul lainnya = 1 + panjang lintasan dari akar ke simpul tersebut • Height (tinggi) atau depth (kedalaman) Ä Adalah level maksimum dari suatu pohon Ä Nama lain : panjang maksimum lintasan dari akar ke daun Ä Pada gambar di samping : Level 0 a e c d 1 2 g f k h i j l m 3 4 Ä Pohon mempunyai height atau depth : 4 Matematika Diskrit 21

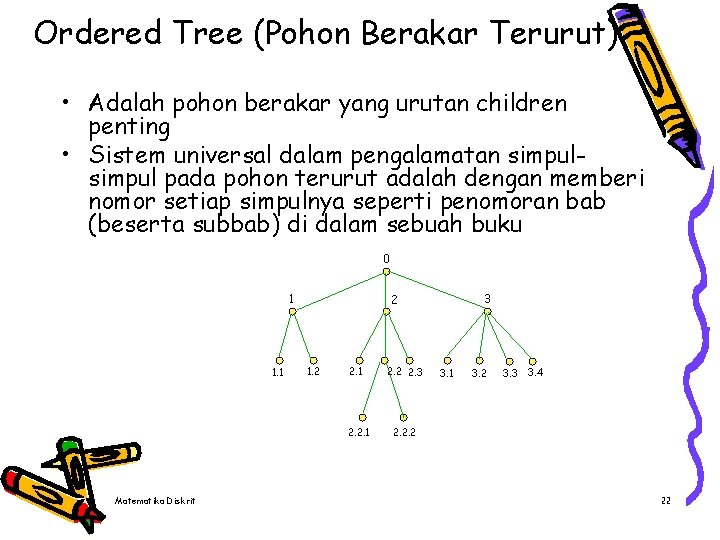
Ordered Tree (Pohon Berakar Terurut) • Adalah pohon berakar yang urutan children penting • Sistem universal dalam pengalamatan simpul pada pohon terurut adalah dengan memberi nomor setiap simpulnya seperti penomoran bab (beserta subbab) di dalam sebuah buku 0 1 1. 2 2. 1 2. 2. 1 Matematika Diskrit 3 2 2. 3 3. 1 3. 2 3. 3 3. 4 2. 2. 2 22

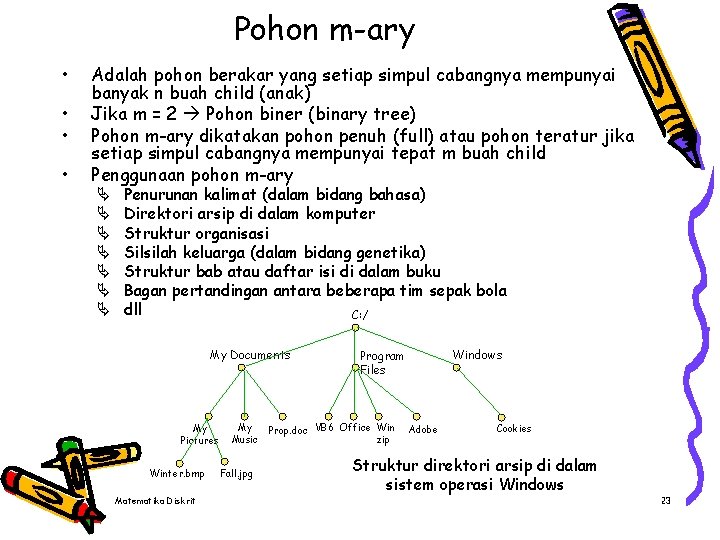
Pohon m-ary • • Adalah pohon berakar yang setiap simpul cabangnya mempunyai banyak n buah child (anak) Jika m = 2 Pohon biner (binary tree) Pohon m-ary dikatakan pohon penuh (full) atau pohon teratur jika setiap simpul cabangnya mempunyai tepat m buah child Penggunaan pohon m-ary Ä Ä Ä Ä Penurunan kalimat (dalam bidang bahasa) Direktori arsip di dalam komputer Struktur organisasi Silsilah keluarga (dalam bidang genetika) Struktur bab atau daftar isi di dalam buku Bagan pertandingan antara beberapa tim sepak bola dll C: / My Documents My Pictures Winter. bmp Matematika Diskrit My Music Fall. jpg Windows Program Files Prop. doc VB 6 Office Win zip Adobe Cookies Struktur direktori arsip di dalam sistem operasi Windows 23

Jumlah Daun pada Pohon m-ary Penuh • Pada pohon m-ary penuh dengan tinggi (height) h, jumlah daun (leaf) adalah : mh • Jika T bukan pohon m-ary penuh jumlah daun mh • Jumlah seluruh simpul pohon m-ary pada pohon m-ary penuh dengan tinggi h : level 0 jumlah simpul = m 0 = 1 level 1 jumlah simpul = m 1 level 2 jumlah simpul = m 2 … level h jumlah simpul = mh sehingga jumlah seluruh simpul adalah : • Sehingga jumlah seluruh simpul untuk T bukan pohon m-ary penuh : Matematika Diskrit 24

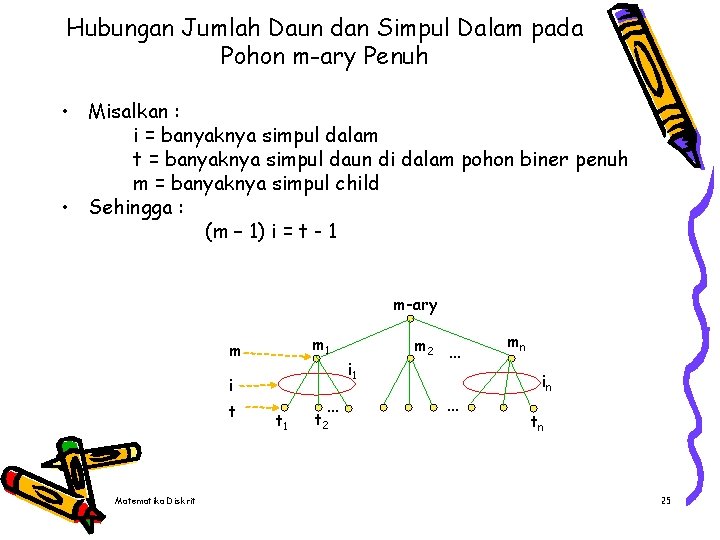
Hubungan Jumlah Daun dan Simpul Dalam pada Pohon m-ary Penuh • Misalkan : i = banyaknya simpul dalam t = banyaknya simpul daun di dalam pohon biner penuh m = banyaknya simpul child • Sehingga : (m – 1) i = t - 1 m-ary m 1 m i 1 i t Matematika Diskrit t 1 … t 2 m 2 … … mn in tn 25

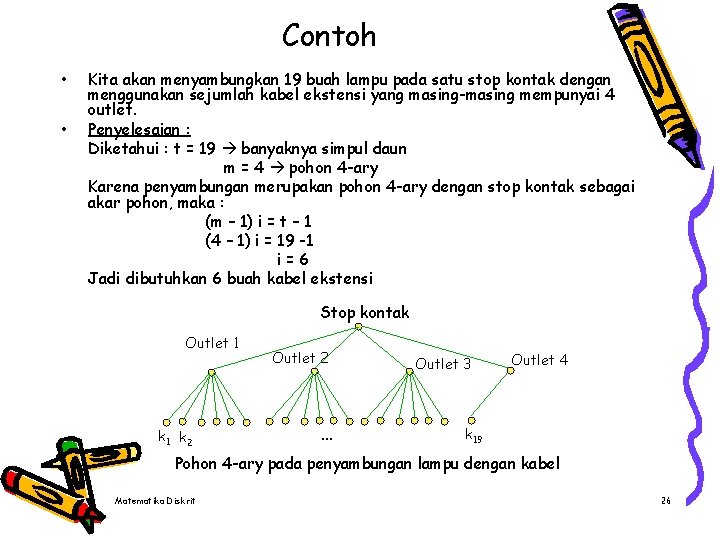
Contoh • • Kita akan menyambungkan 19 buah lampu pada satu stop kontak dengan menggunakan sejumlah kabel ekstensi yang masing-masing mempunyai 4 outlet. Penyelesaian : Diketahui : t = 19 banyaknya simpul daun m = 4 pohon 4 -ary Karena penyambungan merupakan pohon 4 -ary dengan stop kontak sebagai akar pohon, maka : (m – 1) i = t – 1 (4 – 1) i = 19 -1 i=6 Jadi dibutuhkan 6 buah kabel ekstensi Stop kontak Outlet 1 k 2 Outlet 2 … Outlet 3 Outlet 4 k 19 Pohon 4 -ary pada penyambungan lampu dengan kabel Matematika Diskrit 26

• Pohon Biner • Adalah pohon yang setiap simpul cabangnya mempunyai paling banyak 2 buah child (anak) Left subtree (sub pohon kiri) adalah : • Right subtree (sub pohon kanan) adalah : • Skewed tree (pohon condong) adalah : • Skew left (pohon condong kiri) adalah : • Skew right (pohon condong kanan) adalah : • Full binary tree (pohon biner penuh) adalah : • Pohon biner penuh dengan tinggi h memiliki jumlah daun sebanyak 2 h , dan jumlah seluruh simpul adalah : F Pohon yang akarnya adalah left child (anak kiri) F Pohon yang akarnya adalah right child (anak kanan) F Pohon yang semua simpulnya terletak di bagian kiri saja atau bagian kanan saja F Pohon yang condong ke kiri F Pohon yang condong ke kanan F Pohon biner yang setiap simpulnya mempunyai tepat 2 buah child (anak), kiri dan kanan, kecuali simpul pada level bawah Matematika Diskrit Pohon biner penuh 27

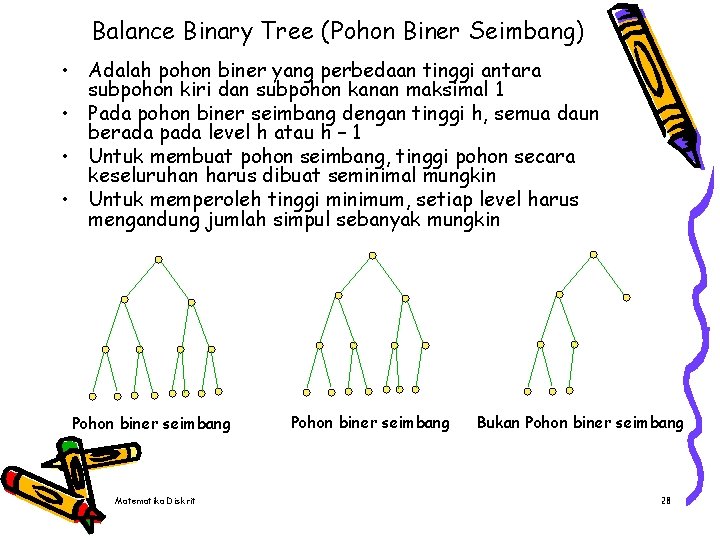
Balance Binary Tree (Pohon Biner Seimbang) • Adalah pohon biner yang perbedaan tinggi antara subpohon kiri dan subpohon kanan maksimal 1 • Pada pohon biner seimbang dengan tinggi h, semua daun berada pada level h atau h – 1 • Untuk membuat pohon seimbang, tinggi pohon secara keseluruhan harus dibuat seminimal mungkin • Untuk memperoleh tinggi minimum, setiap level harus mengandung jumlah simpul sebanyak mungkin Pohon biner seimbang Matematika Diskrit Pohon biner seimbang Bukan Pohon biner seimbang 28

Pohon Ekspresi • • • Adalah pohon biner dengan daun menyatakan operand dan simpul dalam (termasuk akar) menyatakan operator Tanda kurung tidak lagi diperlukan bila suatu ekspresi aritmetik direpresentasikan sebagai pohon biner Pohon ekspresi digunakan oleh compiler bahasa tingkat tinggi untuk mengevaluasi ekspresi yang ditulis dalam notasi : Ä Infix F Operator berada di antara 2 buah operand Ä Prefix (polish notation) F Operator mendahului 2 buah operand-nya Ä Postfix (inverse polish notation) • F Kedua operand mendahului operatornya Contoh : Ä (a + b)*(c/(d + e)) Ä *+ab/c+de Ä ab+cde+/* Matematika Diskrit * + a / b + c d e Pohon ekspresi dari (a + b)*(c/(d + e)) infix prefix postfix 29

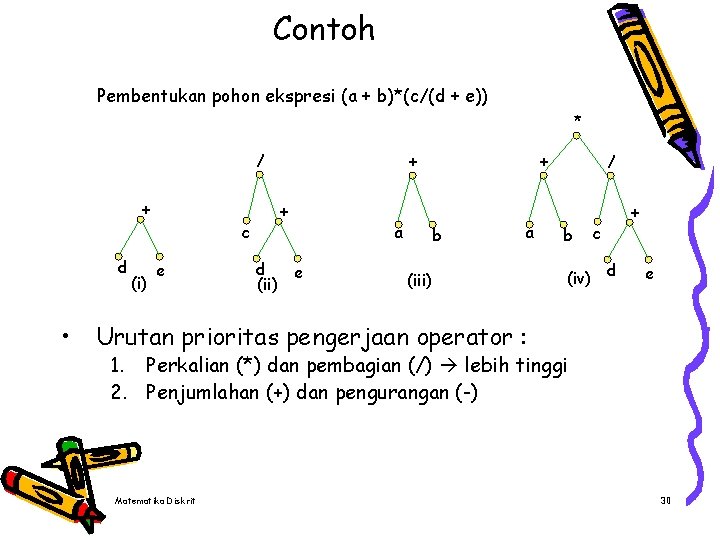
Contoh Pembentukan pohon ekspresi (a + b)*(c/(d + e)) * / + + c d • (i) e + d (ii) a e + b a (iii) / b (iv) + c d e Urutan prioritas pengerjaan operator : 1. Perkalian (*) dan pembagian (/) lebih tinggi 2. Penjumlahan (+) dan pengurangan (-) Matematika Diskrit 30

Pembentukan Pohon Ekspresi dari Notasi Postfix 1. Setiap elemen (operand dan operator) dari notasi postfix yang panjangnya n disimpan di dalam tabel sebagai elemen P 1 , P 2 , …, Pn 1 2 3 4 5 6 7 8 n=9 a b + c d e + / * 2. Tumpukan S menyimpan pointer ke simpul pohon biner (tumpukan tumbuh dari kiri ke kanan) Arah pertumbuhan tumpukan Matematika Diskrit 31

Algoritma pembentukan pohon ekspresi dari notasi postfix Matematika Diskrit 32

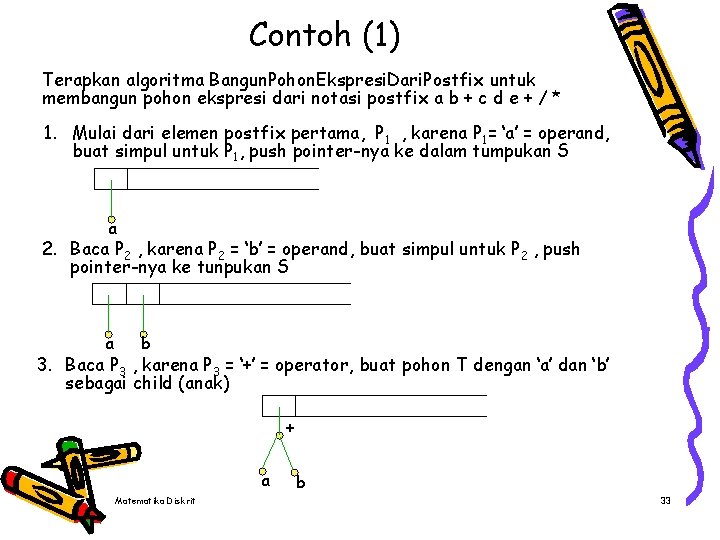
Contoh (1) Terapkan algoritma Bangun. Pohon. Ekspresi. Dari. Postfix untuk membangun pohon ekspresi dari notasi postfix a b + c d e + / * 1. Mulai dari elemen postfix pertama, P 1 , karena P 1= ‘a’ = operand, buat simpul untuk P 1, push pointer-nya ke dalam tumpukan S a 2. Baca P 2 , karena P 2 = ‘b’ = operand, buat simpul untuk P 2 , push pointer-nya ke tunpukan S a b 3. Baca P 3 , karena P 3 = ‘+’ = operator, buat pohon T dengan ‘a’ dan ‘b’ sebagai child (anak) + a Matematika Diskrit b 33

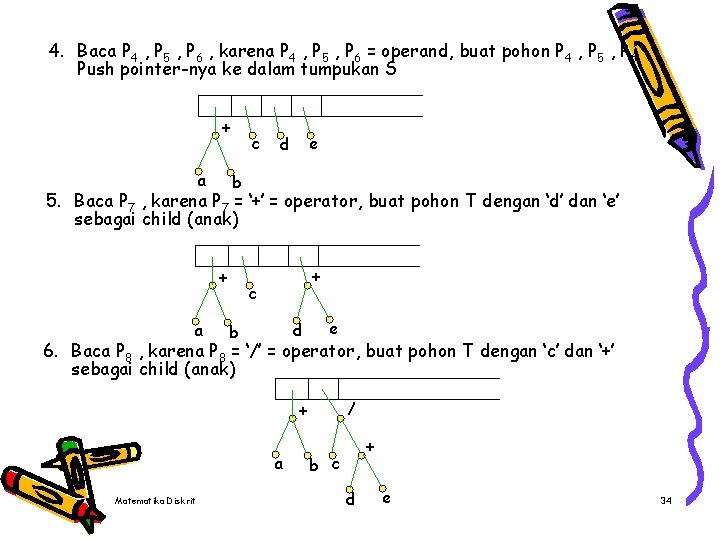
4. Baca P 4 , P 5 , P 6 , karena P 4 , P 5 , P 6 = operand, buat pohon P 4 , P 5 , P 6 Push pointer-nya ke dalam tumpukan S + a c e d b 5. Baca P 7 , karena P 7 = ‘+’ = operator, buat pohon T dengan ‘d’ dan ‘e’ sebagai child (anak) + a + c d b e 6. Baca P 8 , karena P 8 = ‘/’ = operator, buat pohon T dengan ‘c’ dan ‘+’ sebagai child (anak) / + a Matematika Diskrit + b c d e 34

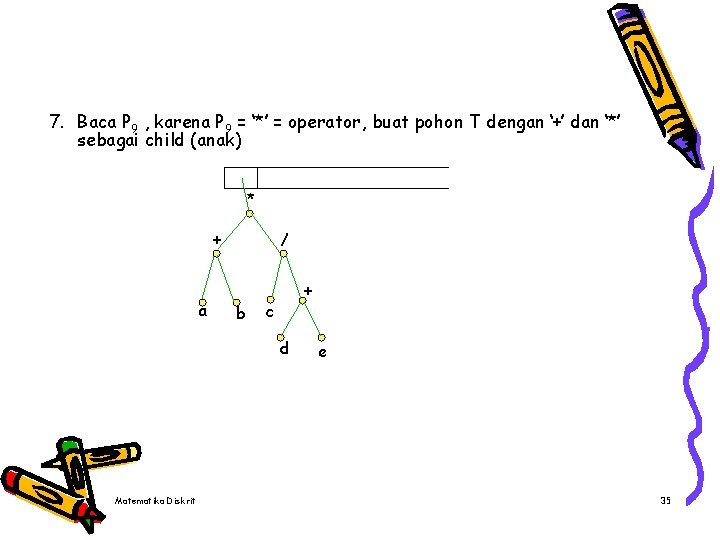
7. Baca P 9 , karena P 9 = ‘*’ = operator, buat pohon T dengan ‘+’ dan ‘*’ sebagai child (anak) * + a / b + c d Matematika Diskrit e 35

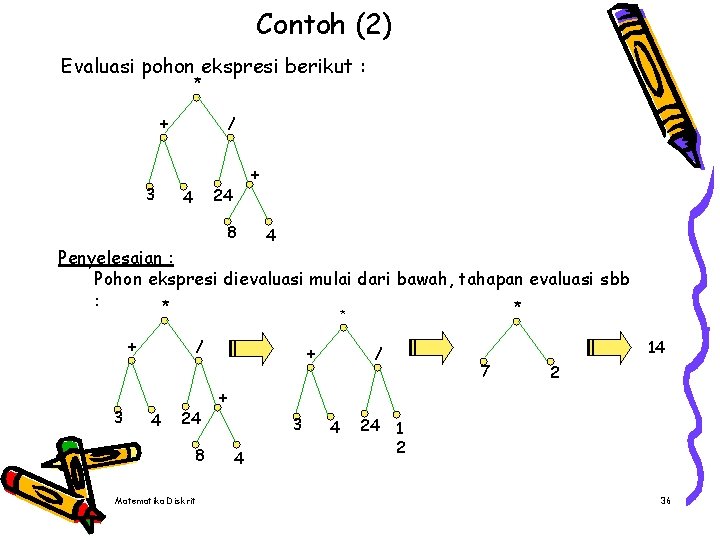
Contoh (2) Evaluasi pohon ekspresi berikut : * + 3 / + 24 4 8 4 Penyelesaian : Pohon ekspresi dievaluasi mulai dari bawah, tahapan evaluasi sbb : * * * + 3 / 4 24 8 Matematika Diskrit + 14 / 7 2 + 3 4 4 24 1 2 36

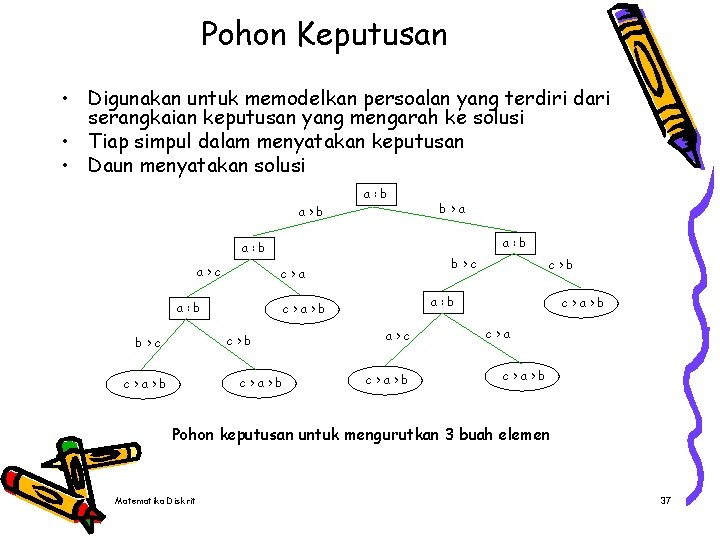
Pohon Keputusan • Digunakan untuk memodelkan persoalan yang terdiri dari serangkaian keputusan yang mengarah ke solusi • Tiap simpul dalam menyatakan keputusan • Daun menyatakan solusi a: b a>b a: b a>c c>a>b c>b a: b c>a>b b>c c>a a: b b>c b>a a>c c>a>b Pohon keputusan untuk mengurutkan 3 buah elemen Matematika Diskrit 37

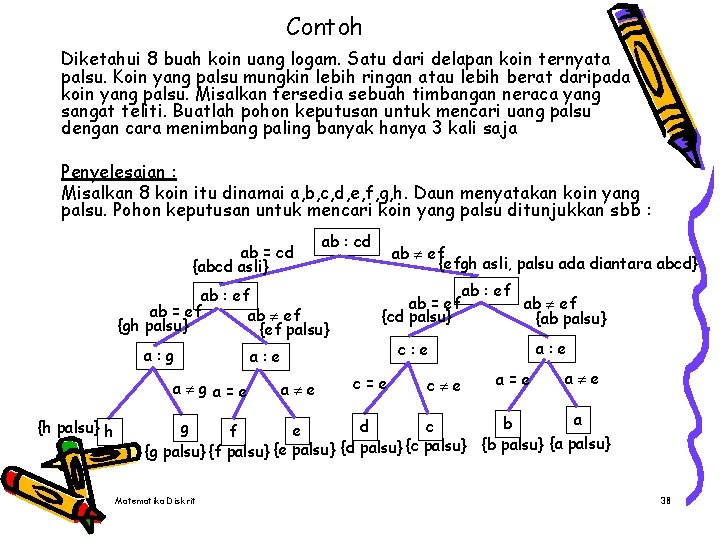
Contoh Diketahui 8 buah koin uang logam. Satu dari delapan koin ternyata palsu. Koin yang palsu mungkin lebih ringan atau lebih berat daripada koin yang palsu. Misalkan tersedia sebuah timbangan neraca yang sangat teliti. Buatlah pohon keputusan untuk mencari uang palsu dengan cara menimbang paling banyak hanya 3 kali saja Penyelesaian : Misalkan 8 koin itu dinamai a, b, c, d, e, f, g, h. Daun menyatakan koin yang palsu. Pohon keputusan untuk mencari koin yang palsu ditunjukkan sbb : ab = cd {abcd asli} ab : cd ab : ef ab = ef ab ef {gh palsu} {ef palsu} a: g ab = ef {cd palsu} a e ab : ef ab ef {ab palsu} a: e c: e a ga=e {h palsu} h ab ef {efgh asli, palsu ada diantara abcd} c=e c e a=e a b d c e f {g palsu} {f palsu} {e palsu} {d palsu} {c palsu} {b palsu} {a palsu} g Matematika Diskrit 38

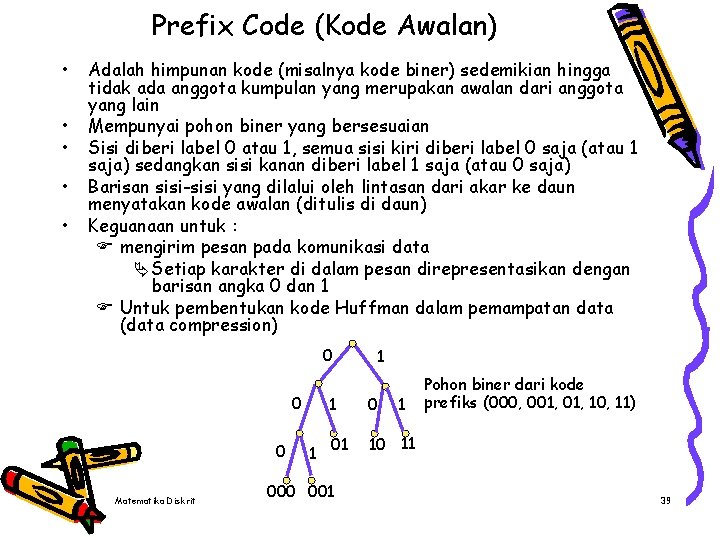
Prefix Code (Kode Awalan) • • • Adalah himpunan kode (misalnya kode biner) sedemikian hingga tidak ada anggota kumpulan yang merupakan awalan dari anggota yang lain Mempunyai pohon biner yang bersesuaian Sisi diberi label 0 atau 1, semua sisi kiri diberi label 0 saja (atau 1 saja) sedangkan sisi kanan diberi label 1 saja (atau 0 saja) Barisan sisi-sisi yang dilalui oleh lintasan dari akar ke daun menyatakan kode awalan (ditulis di daun) Keguanaan untuk : F mengirim pesan pada komunikasi data Ä Setiap karakter di dalam pesan direpresentasikan dengan barisan angka 0 dan 1 F Untuk pembentukan kode Huffman dalam pemampatan data (data compression) 0 0 0 Matematika Diskrit 1 1 1 0 01 10 11 000 001 1 Pohon biner dari kode prefiks (000, 001, 10, 11) 39

Kode Huffman • Pemampatan data dilakukan dengan mengkodekan setiap karakter di dalam pesan atau di dalam arsip dikodekan dengan kode yang lebih pendek • Sistem kode yang banyak digunakan adalah kode ASCII (setiap karakter dikodekan dalam 8 bit biner) • Cara pembentuka kode Huffman dengan membentuk pohon biner (dinamakan dengan pohon Huffman) yaitu : 1. Pilih 2 simbol dengan peluang (probability) paling kecil sebagai child kemudian kedua simbol tersebut dikombinasikan sebagai parent peluang penjumlahan dari kedua simbol tersebut 2. Pilih 2 simbol berikutnya termasuk simbol baru yang mempunyai peluang kecil sebagai child kemudian kedua simbol tersebut dikombinasikan sebagai parent peluang penjumlahan dari kedua simbol tersebut 3. Prosedur yang sama dilakukan pada 2 simbol berikutnya yang mempunyai peluang terkecil sebagai child kemudian kedua simbol tersebut dikombinasikan sebagai parent peluang penjumlahan dari kedua simbol tersebut Matematika Diskrit 40

Kode Huffman (Lanj. ) • Kode Huffman tidak bersifat unik, artinya kode untuk setiap karakter berbeda-beda pada setiap pesan bergantung pada kekerapan kemunculan karakter tersebut di dalam pesan • Keputusan apakah suatu simpul pada pohon Huffman diletakkan di kiri atau di kanan menentukan kode yang dihasilkan (tetapi tidak mempengaruhi panjang kodenya) Matematika Diskrit 41

Contoh (1) Representasikan string ‘ABACCDA’ dalam kode ASCII dan kode Huffman • Kode ASCII Simbol Kode ASCII A 01000001 B 01000010 C 01000011 D 0100 String ‘ABACCDA’ direpresintasikan menjadi rangkaian : 01000001010000100100000101000011010001000001 Representasi 7 huruf tersebut membutuhkan 7 x 8 bit = 56 bit (7 byte) Matematika Diskrit 42

• Kode Huffman Simbol Kekerapan Peluang A 3 3/7 B 1 1/7 C 2 2/7 D 1 1/7 Cara pembentukan kode Huffman : 1. Pilih 2 simbol dengan peluang paling kecil, yaitu simbol B dan D. Simbol tersebut dikombinasikan menjadi simbol BD dengan peluang 1/7 + 1/7 = 2/7 2. Pilih 2 simbol dengan peluang paling kecil, yaitu simbol C dan BD. Simbol tersebut dikombinasikan menjadi simbol CBD dengan peluang 2/7 + 2/7 = 4/7 3. Pilih 2 simbol dengan peluang paling kecil, yaitu simbol A dan CBD. Simbol tersebut dikombinasikan menjadi simbol ACBD dengan peluang 4/7 + 3/7 = 7/7 = 1 Matematika Diskrit 43

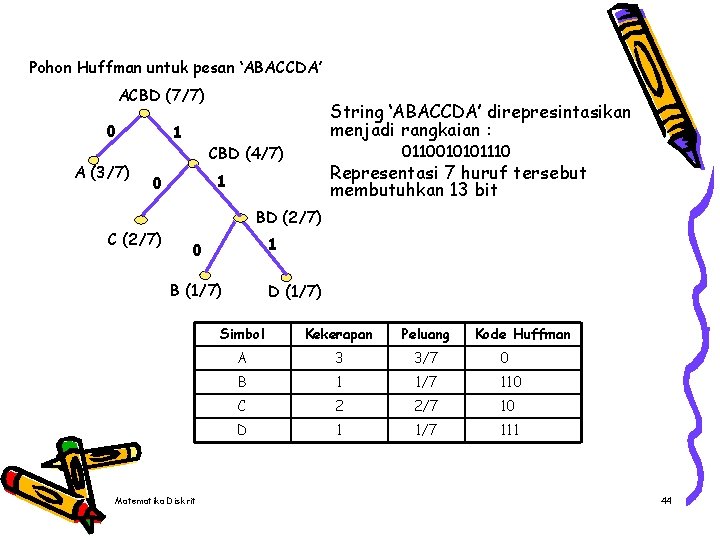
Pohon Huffman untuk pesan ‘ABACCDA’ ACBD (7/7) 0 A (3/7) 1 0110010101110 CBD (4/7) Representasi 7 huruf tersebut membutuhkan 13 bit 1 0 C (2/7) String ‘ABACCDA’ direpresintasikan menjadi rangkaian : BD (2/7) 1 0 B (1/7) Matematika Diskrit D (1/7) Simbol Kekerapan Peluang Kode Huffman A 3 3/7 0 B 1 1/7 110 C 2 2/7 10 D 1 1/7 111 44

Binary Search Tree (Pohon Pencarian Biner) • • Adalah pohon biner yang setiap key diatur dalam suatu urutan tertentu Digunakan untuk melakukan operasi • Simpul pada pohon pencarian berupa field kunci (key) pada : • Key (kunci) adalah : • Key harus unik, karena itu tidak ada 2 buah simpul atau lebih yang mempunyai kunci yang sama Jika R adalah akar dan semua key yang tersimpan pada setiap simpul tidak ada yang sama maka : : • Ä Pencarian Ä Penyisipan Ä Penghapusan elemen Ä Data record atau Ä Data itu sendiri F Nilai yang membedakan setiap simpul dengan simpul yang lainnya Ä Semua simpul pada subpohon kiri mempunyai key lebih kecil dari key R Ä Semua simpul di subpohon kanan mempunyai key nilai lebih besar dari key R R Matematika Diskrit T 1 Key T 1 < key R Key T 2 > key R T 2 45

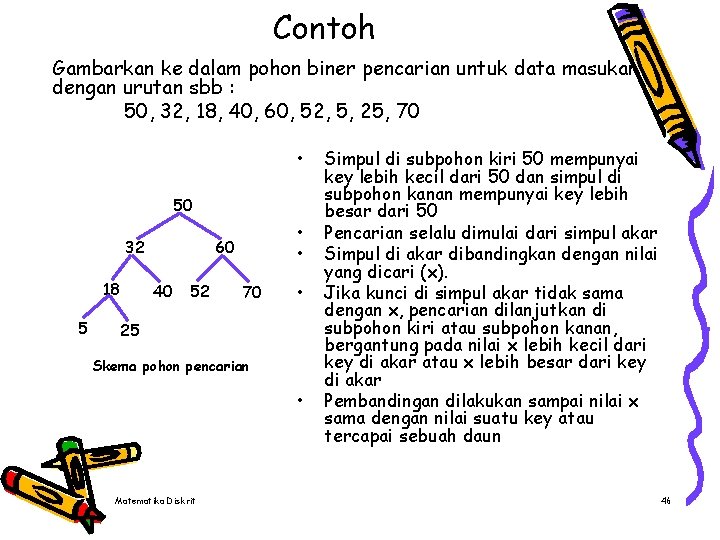
Contoh Gambarkan ke dalam pohon biner pencarian untuk data masukan dengan urutan sbb : 50, 32, 18, 40, 60, 52, 5, 25, 70 • 50 32 18 5 • • 60 40 52 70 • 25 Skema pohon pencarian • Matematika Diskrit Simpul di subpohon kiri 50 mempunyai key lebih kecil dari 50 dan simpul di subpohon kanan mempunyai key lebih besar dari 50 Pencarian selalu dimulai dari simpul akar Simpul di akar dibandingkan dengan nilai yang dicari (x). Jika kunci di simpul akar tidak sama dengan x, pencarian dilanjutkan di subpohon kiri atau subpohon kanan, bergantung pada nilai x lebih kecil dari key di akar atau x lebih besar dari key di akar Pembandingan dilakukan sampai nilai x sama dengan nilai suatu key atau tercapai sebuah daun 46

Traversal Pohon Biner • Misalkan T adalah pohon biner, akarnya R, subpohon kiri T 1 dan subpohon kanan T 2 maka ada skema mengunjungi simpul di dalam pohon biner T : 1. Preorder Ä Kunjungi R (sekaligus memproses simpul R) Ä Kunjungi T 1 secara preorder Ä Kunjungi T 2 secara preorder 2. Inorder Ä Kunjungi T 1 secara inorder Ä Kunjungi R (sekaligus memproses simpul R) Ä Kunjungi T 2 secara inorder 3. Postorder Ä Kunjungi T 1 secara postorder Ä Kunjungi T 2 secara postorder Ä Kunjungi R (sekaligus memproses simpul R) • Proses yang dilakukan terhadap simpul yang dikunjungi misalnya Ä mencetak informasi yang disimpan di dalam simpul Ä Memanipulasi nilai, dll Matematika Diskrit 47

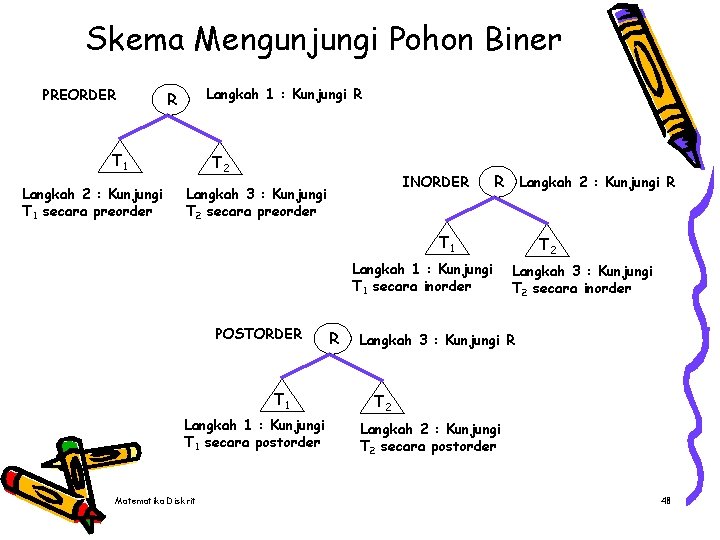
Skema Mengunjungi Pohon Biner PREORDER Langkah 1 : Kunjungi R R T 1 Langkah 2 : Kunjungi T 1 secara preorder T 2 INORDER Langkah 3 : Kunjungi T 2 secara preorder R Langkah 2 : Kunjungi R T 1 Langkah 1 : Kunjungi T 1 secara inorder POSTORDER T 1 Langkah 1 : Kunjungi T 1 secara postorder Matematika Diskrit R T 2 Langkah 3 : Kunjungi T 2 secara inorder Langkah 3 : Kunjungi R T 2 Langkah 2 : Kunjungi T 2 secara postorder 48

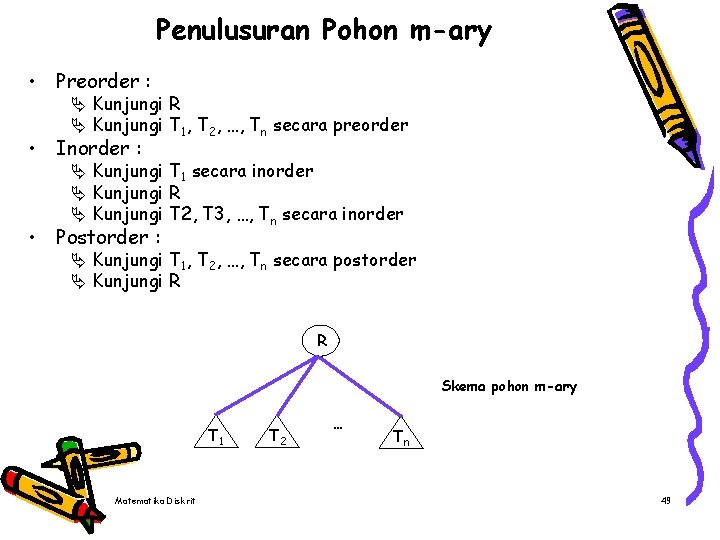
Penulusuran Pohon m-ary • Preorder : Ä Kunjungi R Ä Kunjungi T 1, T 2, …, Tn secara preorder • Inorder : Ä Kunjungi T 1 secara inorder Ä Kunjungi R Ä Kunjungi T 2, T 3, …, Tn secara inorder • Postorder : Ä Kunjungi T 1, T 2, …, Tn secara postorder Ä Kunjungi R R Skema pohon m-ary T 1 Matematika Diskrit T 2 … Tn 49

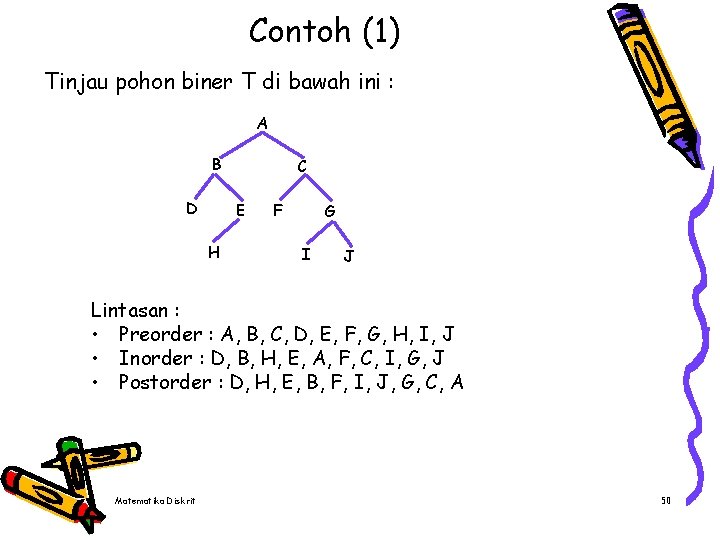
Contoh (1) Tinjau pohon biner T di bawah ini : A B D C E H F G I J Lintasan : • Preorder : A, B, C, D, E, F, G, H, I, J • Inorder : D, B, H, E, A, F, C, I, G, J • Postorder : D, H, E, B, F, I, J, G, C, A Matematika Diskrit 50

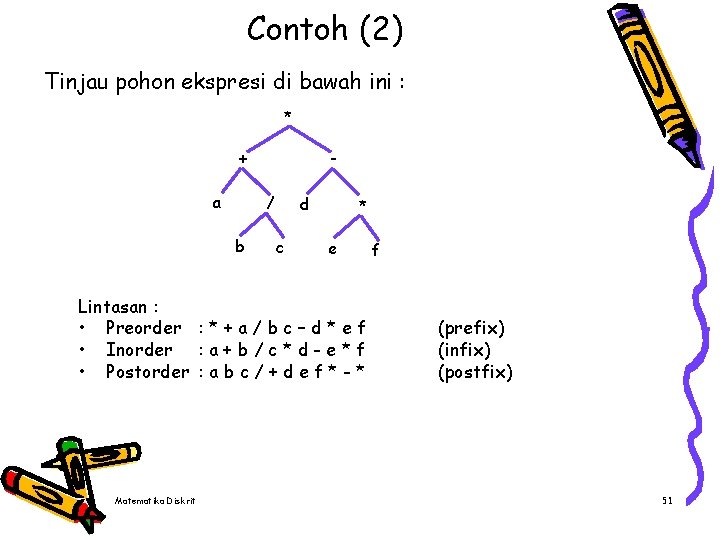
Contoh (2) Tinjau pohon ekspresi di bawah ini : * + a / b d c * e Lintasan : • Preorder : * + a / b c – d * e f • Inorder : a + b / c * d - e * f • Postorder : a b c / + d e f * - * Matematika Diskrit f (prefix) (infix) (postfix) 51

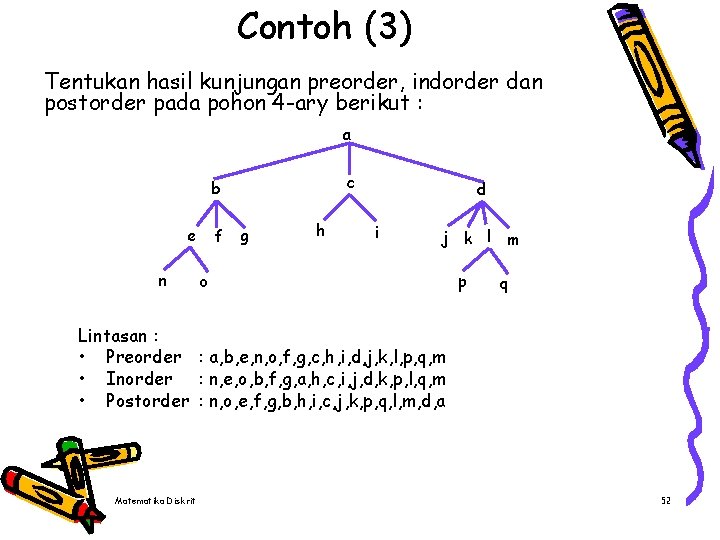
Contoh (3) Tentukan hasil kunjungan preorder, indorder dan postorder pada pohon 4 -ary berikut : a c b e n f g h d i j k l o p m q Lintasan : • Preorder : a, b, e, n, o, f, g, c, h, i, d, j, k, l, p, q, m • Inorder : n, e, o, b, f, g, a, h, c, i, j, d, k, p, l, q, m • Postorder : n, o, e, f, g, b, h, i, c, j, k, p, q, l, m, d, a Matematika Diskrit 52

Latihan Soal Matematika Diskrit 53