Kuliah 3 2 HIMPUNAN Matematika Diskrit Dr Ing

Kuliah 3 2. HIMPUNAN Matematika Diskrit Dr. -Ing. Erwin Sitompul http: //zitompul. wordpress. com

Pekerjaan Rumah (PR 2) No. 1: Diberikan pernyataan “Perlu memiliki password yang sah agar Anda bisa log on ke server. ” a) Nyatakanlah pernyataan di atas dalam bentuk proposisi “jika p maka q. ” b) Tentukanlah ingkaran, konversi, inversi, dan kontraposisi dari pernyataan tersebut. No. 2: Periksa kesahihan argumen berikut ini: “Jika 5 lebih kecil dari 4, maka 5 bukan bilangan prima. ” “ 5 tidak lebih kecil dari 4. ” “ 5 adalah bilangan prima. ” Erwin Sitompul Matematika Diskrit 3/2

No. 1: Solusi Pekerjaan Rumah (PR 2) Diberikan pernyataan “Perlu memiliki password yang sah agar Anda bisa log on ke server. ” q syarat perlu untuk p Solusi: a) “Jika Anda bisa log on ke server, maka Anda memiliki password yang sah. ” Ingkaran: ~(p q) p ~q b) Ingkaran: “Anda bisa log on ke server dan (walaupun) Anda tidak memiliki password yang sah. ” Konversi: q p Konversi: “Jika Anda memiliki password yang sah, maka Anda bisa log on ke server. ” Inversi: ~p ~q Inversi: “Jika Anda tidak bisa log on ke server, maka Anda tidak memiliki password yang sah. ” Kontraposisi: ~q ~p Kontraposisi: “Jika Anda tidak memiliki password yang sah, maka Anda tidak bisa log on ke server. ” Erwin Sitompul Matematika Diskrit 3/3

No. 2: Solusi Pekerjaan Rumah (PR 2) Periksa kesahihan argumen berikut ini: “Jika 5 lebih kecil dari 4, maka 5 bukan bilangan prima. ” “ 5 tidak lebih kecil dari 4. ” “ 5 adalah bilangan prima. ” Solusi: Misalkan: p : 5 lebih kecil dari 4. q : 5 bukan bilangan prima. Maka argumen di atas dapat dituliskan dengan: p q ~p ~q § Perhatikan baris 3 § Konklusi ~q salah, walaupun semua hipotesis benar § Jadi, argumen tersebut tidak sahih atau p a l s u Erwin Sitompul Matematika Diskrit 3/4

Terminologi Himpunan (set) adalah kumpulan obyek-obyek yang berbeda. Obyek di dalam himpunan disebut elemen, unsur, atau anggota. Contoh: § HIPMI, HKTI, Paguyuban Pasundan, dll, dimana tiap anggota berbeda satu sama lain. § PSSI, APKASI, PBB. § PUSU (President University Student Union). § Satu set huruf (besar dan kecil). Erwin Sitompul Matematika Diskrit 3/5

Cara Penulisan Himpunan 1. Enumerasi Penulisan setiap anggota himpunan dilakukan secara rinci. Contoh: § Himpunan empat bilangan asli pertama: A = { 1, 2, 3, 4 }. § Himpunan lima bilangan genap positif pertama: B = { 2, 4, 6, 8, 10 }. § C = { kucing, a, Amir, 10, paku }. § R = { a, b, {a, b, c}, {a, c} }. § C = { a, {a}, {{a}} }. § K = { {} }, dimana {} adalah himpunan kosong. § Himpunan 100 buah bilangan asli pertama: { 1, 2, . . . , 100 }. § Himpunan bilangan bulat ditulis sebagai: {…, – 2, – 1, 0, 1, 2, …}. Erwin Sitompul Matematika Diskrit 3/6

Cara Penulisan Himpunan Keanggotaan x A : x merupakan anggota himpunan A. x A : x bukan merupakan anggota himpunan A. Contoh: Misalkan A = { 1, 2, 3, 4 }, R = { a, b, {a, b, c}, {a, c} }, K ={ {} }, maka: § 3 A § { a, b, c } R § {c} R § {} K § {} R Erwin Sitompul Matematika Diskrit 3/7

Cara Penulisan Himpunan Contoh: Jika P 1 = { a, b }, P 2 = { { a, b } }, P 3 = { { { a, b } } }, maka a P 1 a P 2 P 1 P 3 P 2 P 3 Erwin Sitompul Matematika Diskrit 3/8

Cara Penulisan Himpunan 2. Simbol-Simbol Baku P N Z Q R C = = = himpunan bilangan bulat positif = { 1, 2, 3, . . . }. himpunan bilangan asli = { 1, 2, . . . }. himpunan bilangan bulat = {. . . , – 2, – 1, 0, 1, 2, . . . }. himpunan bilangan rasional (pecahan). himpunan bilangan riil. himpunan bilangan kompleks. Himpunan yang universal disebut: semesta, dan disimbolkan dengan U. Contoh: Misalkan U = { 1, 2, 3, 4, 5 }, maka A adalah himpunan bagian dari U, dimana A = { 1, 3, 5 }. Erwin Sitompul Matematika Diskrit 3/9

Cara Penulisan Himpunan 3. Notasi Pembentuk Himpunan Notasi: { x | syarat yang harus dipenuhi oleh x }. Contoh: a) A adalah himpunan bilangan bulat positif kecil dari 5. A = { x | x bilangan bulat positif lebih kecil dari 5 }. A = { x | x P, x < 5 }. A = { 1, 2, 3, 4 }. b) M = { x | x adalah mahasiswa yang menghadiri kuliah Matematika Diskrit hari ini}. Erwin Sitompul Matematika Diskrit 3/10

Cara Penulisan Himpunan 4. Diagram Venn Merupakan suatu cara untuk mengilustrasikan hubungan antar himpunan secara grafis. Contoh: Misalkan U = { 1, 2, …, 7, 8 }, A = { 1, 2, 3, 5 }, dan B = { 2, 5, 6, 8 }. Diagram Venn: Erwin Sitompul Matematika Diskrit 3/11

Kardinalitas Jumlah anggota di dalam himpunan A disebut kardinal dari himpunan A. Notasi: n(A) atau A. Contoh: a) B = { x | x merupakan bilangan prima lebih kecil dari 20 }, B = { 2, 3, 5, 7, 11, 13, 17, 19 }, maka B = 8. b) T = { kucing, a, Amir, 10, paku }, maka T = 5. c) A = { a, {a}, {{a}} }, maka A = 3. Erwin Sitompul Matematika Diskrit 3/12

Himpunan Kosong (Null Set) Himpunan dengan kardinal = 0 disebut himpunan kosong (null set). Notasi: atau { }. Contoh: a) E = { x | x < x }, maka n(E) = 0 E = atau E = { }. b) P = { orang Indonesia yang pernah ke bulan }, maka n(P) = 0 P = atau P = { }. c) A = { x | x adalah akar riil dari persamaan kuadrat x 2 + 1 = 0 }, maka n(A) = 0 A = atau A = { }. Erwin Sitompul Matematika Diskrit 3/13

Himpunan Kosong (Null Set) § Himpunan { {} } dapat juga ditulis sebagai { }. § Himpunan { {}, {{}} } dapat juga ditulis sebagai { , { }}. § { } bukan himpunan kosong karena ia memuat satu anggota yaitu himpunan kosong. Erwin Sitompul Matematika Diskrit 3/14

Himpunan Bagian (Subset) Himpunan A dikatakan himpunan bagian dari B jika dan hanya jika setiap anggota A merupakan anggota dari B. Dalam hal ini, B dikatakan superset dari A. Notasi: A B Erwin Sitompul Matematika Diskrit 3/15

Himpunan Bagian (Subset) Contoh: a) { 1, 2, 3 } { 1, 2, 3, 4, 5 }. b) { 1, 2, 3 }. c) N Z R C. d) Jika A = { (x, y) | x + y < 4, x 0, y 0 } dan B = { (x, y) | 2 x + y < 4, x 0 dan y 0 }, maka B A. Teorema 1. Untuk sembarang himpunan A berlaku hal-hal sebagai berikut: a) A adalah himpunan bagian dari A itu sendiri (A A). b) Himpunan kosong adalah himpunan bagian dari A ( A). c) Jika A B dan B C, maka A C. Erwin Sitompul Matematika Diskrit 3/16

Proper dan Improper Subset Pada A dan A A, maka dan A disebut himpunan bagian tak sebenarnya (improper subset) dari himpunan A. Contoh: Bila A = { 1, 2, 3 }, maka { 1, 2, 3 } dan adalah improper subset dari A. § A B berbeda dengan A B. § A B : A adalah himpunan bagian dari B, tetapi tidak dimungkinkan A B (A adalah proper subset dari B). § A B : A adalah himpunan bagian dari B yang memungkinkan A = B (A adalah improper subset dari B). Erwin Sitompul Matematika Diskrit 3/17

Proper dan Improper Subset Contoh: Misalkan A = { 1, 2, 3 } dan B = { 1, 2, 3, 4, 5 }. Tentukan semua kemungkinan himpunan C sedemikian sehingga A C dan C B, yaitu A adalah proper subset dari C dan C adalah proper subset dari B. Solusi: C harus mengandung semua anggota A = { 1, 2, 3 } dan sedikitnya satu anggota dari B yang bukan anggota A. Dengan demikian, C = { 1, 2, 3, 4 } atau C = { 1, 2, 3, 5 }. C tidak boleh memuat 4 dan 5 sekaligus karena C adalah proper subset dari B. Erwin Sitompul Matematika Diskrit 3/18

Himpunan Identik § A = B (A identik B) jika dan hanya jika setiap anggota A merupakan anggota B dan sebaliknya setiap anggota B merupakan anggota A. § A = B jika A adalah himpunan bagian dari B dan B adalah himpunan bagian dari A. Jika tidak demikian, maka A B. § Notasi: A = B A B dan B A Contoh: a) Jika A = { 0, 1 } dan B = { x | x(x – 1) = 0 }, maka A = B. b) Jika A = { 3, 5, 8, 5 } dan B = { 5, 3, 8 }, maka A = B. c) Jika A = { 3, 5, 8, 5 } dan B = { 3, 8 }, maka A B. Erwin Sitompul Matematika Diskrit 3/19

Himpunan Ekivalen § Himpunan A dikatakan ekivalen dengan himpunan B jika dan hanya jika kardinal dari kedua himpunan tersebut sama. § Notasi: A ~ B A = B Contoh: Misalkan A = { 1, 3, 5, 7 } dan B = { a, b, c, d }, maka A ~ B, sebab A = B = 4. Erwin Sitompul Matematika Diskrit 3/20

Himpunan Saling Lepas § Dua himpunan A dan B dikatakan saling lepas (disjoint) jika keduanya tidak memiliki anggota yang sama. § Notasi: A // B Contoh: Jika A = { x | x P, x < 8 } dan B = { 10, 20, 30, . . . }, maka A // B. Erwin Sitompul Matematika Diskrit 3/21

Himpunan Kuasa § Himpunan kuasa (power set) dari himpunan A adalah suatu himpunan yang anggotanya merupakan semua himpunan bagian dari A, termasuk himpunan kosong dan himpunan A sendiri. § Notasi : P(A) atau 2 A § Bila A = m, maka P(A) = 2 m. Contoh: § Jika A = { 1, 2 }, maka P(A) = { , { 1 }, { 2 }, { 1, 2 }}. § Jika T = {kucing, Amir, paku}, maka P(T) = { , {kucing}, {Amir}, {paku}, {kucing, Amir}, {kucing, paku}, {Amir, paku}, {kucing, Amir, paku} }. Erwin Sitompul Matematika Diskrit 3/22

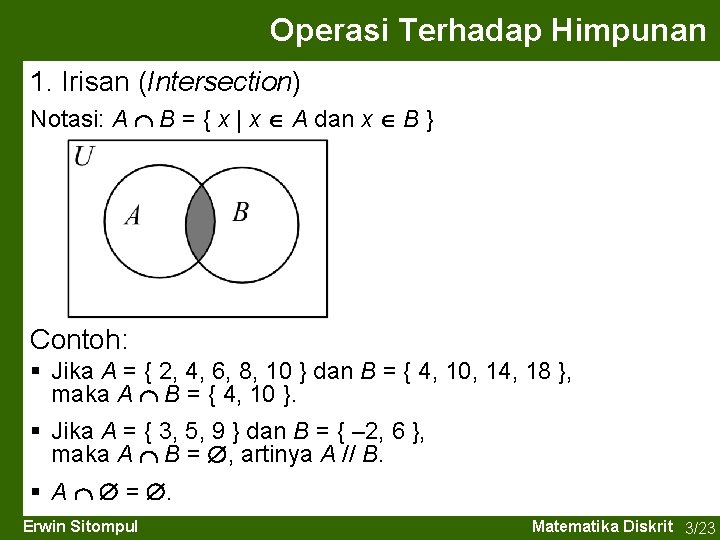
Operasi Terhadap Himpunan 1. Irisan (Intersection) Notasi: A B = { x | x A dan x B } Contoh: § Jika A = { 2, 4, 6, 8, 10 } dan B = { 4, 10, 14, 18 }, maka A B = { 4, 10 }. § Jika A = { 3, 5, 9 } dan B = { – 2, 6 }, maka A B = , artinya A // B. § A = . Erwin Sitompul Matematika Diskrit 3/23

Operasi Terhadap Himpunan 2. Gabungan (Union) Notasi: A B = { x | x A atau x B } Contoh: § Jika A = { 2, 5, 8 } dan B = { 7, 5, 22 }, maka A B = { 2, 5, 7, 8, 22 }. § A = A. Erwin Sitompul Matematika Diskrit 3/24

Operasi Terhadap Himpunan 3. Komplemen (Complement) Notasi: A = { x | x U dan x A } Contoh: § Misalkan U = { a, b, c, d, e, f, g, h, i, j }. Jika A = { a, c, d, f, h, i }, maka A = { b, e, g, j }. § Misalkan U = { x | x P dan x < 9 }. Jika B = { x | x/2 P dan x < 9 }, maka B = { 1, 3, 5, 7 }. Erwin Sitompul Matematika Diskrit 3/25

Operasi Terhadap Himpunan Contoh: Misalkan: A = Himpunan semua mobil buatan dalam negeri B = Himpunan semua mobil impor C = Himpunan semua mobil yang dibuat sebelum tahun 2005 D = Himpunan semua mobil yang nilai jualnya kurang dari Rp 150 juta E = Himpunan semua mobil milik mahasiswa PU (E A) (E B) E (A B) Maka: a) “Semua mobil milik mahasiswa PU yang diproduksi di dalam negeri atau diimpor dari luar negeri. ” A C D b) “Semua mobil produksi dalam negeri yang dibuat sebelum tahun 2005 yang nilai jualnya kurang dari Rp. 150 juta. ” c) “Semua mobil impor buatan setelah tahun 2005 yang mempunyai nilai jual lebih dari Rp. 150 juta. ” B C D Erwin Sitompul Matematika Diskrit 3/26

Operasi Terhadap Himpunan 4. Selisih (Difference) Notasi: A – B = { x | x A dan x B } = A B Contoh: § Jika A = { 1, 2, 3, . . . , 10 } dan B = { 2, 4, 6, 8, 10 }, maka A – B = { 1, 3, 5, 7, 9 } dan B – A = . § { 1, 3, 5 } – { 1, 2, 3 } = { 5 }, tetapi { 1, 2, 3 } – { 1, 3, 5 } = { 2 }. Erwin Sitompul Matematika Diskrit 3/27

Operasi Terhadap Himpunan 5. Selisih Simetris (Symmetric Difference) Notasi: A B = (A B) – (A B) = (A – B) (B – A) Contoh: Jika A = { 2, 4, 6 } dan B = { 2, 3, 5 }, maka A B = { 3, 4, 5, 6 }. Erwin Sitompul Matematika Diskrit 3/28

Operasi Terhadap Himpunan Contoh: Misalkan: U = Himpunan mahasiswa P = Himpunan mahasiswa dengan nilai UTS > 80 Q = Himpunan mahasiswa dengan nilai UAS > 80 Seorang mahasiswa mendapat nilai A jika nilai UTS dan nilai UAS keduanya di atas 80, mendapat nilai B jika salah satu ujian di atas 80, dan mendapat nilai C jika kedua ujian di bawah 80. Maka: a)“Semua mahasiswa yang P Q mendapat nilai A. ” b)“Semua mahasiswa yang mendapat nilai B. ” P Q c)“Semua mahasiswa yang mendapat nilai C. ” U–(P Q) P Q Erwin Sitompul Matematika Diskrit 3/29

Operasi Terhadap Himpunan 5. Perkalian Kartesian (Cartesian Product) Notasi: A B = { (a, b) | a A atau b B } Contoh: § Misalkan C = { 1, 2, 3 } dan D = { a, b }, maka C D = { (1, a), (1, b), (2, a), (2, b), (3, a), (3, b) }. § Misalkan I = Himpunan semua bilangan riil pada sumbu x, J = Himpunan semua bilangan riil pada sumbu y. Maka I J = Himpunan semua titik pada bidang datar xy. Erwin Sitompul Matematika Diskrit 3/30

Operasi Terhadap Himpunan Catatan: 1. Jika A dan B merupakan himpunan berhingga, maka A B = A. B. 2. (a, b) (b, a). 3. A B B A, dengan syarat A atau B tidak kosong. 4. Jika A = atau B = , maka A B = B A = . Contoh: § Sebelumnya, C = { 1, 2, 3 } dan D = { a, b }, C D = { (1, a), (1, b), (2, a), (2, b), (3, a), (3, b) }. D C = { (a, 1), (a, 2), (a, 3), (b, 1), (b, 2), (b, 3) }. C D D C Erwin Sitompul Matematika Diskrit 3/31

Operasi Terhadap Himpunan Contoh: Misalkan A = Himpunan makanan = { s=soto, g=gado-gado, n=nasi goreng, m=mie rebus } J = Himpunan minuman = { c=coca-cola, t=teh, d=es dawet } Berapa banyak kombinasi makanan dan minuman yang dapat disusun dari kedua himpunan di atas? Solusi: A B = 4 3 = 12 kombinasi, yaitu: { (s, c), (s, t), (s, d), (g, c), (g, t), (g, d), (n, c), (n, t), (n, d), (m, c), (m, t), (m, d) }. Erwin Sitompul Matematika Diskrit 3/32

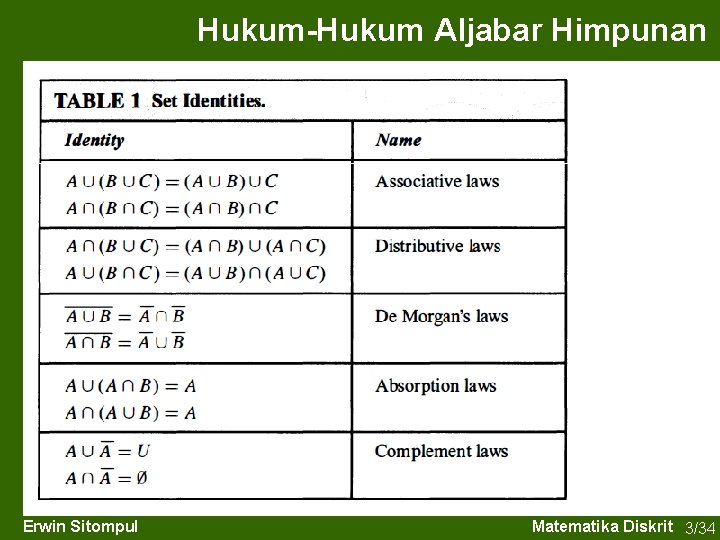
Hukum-Hukum Aljabar Himpunan Erwin Sitompul Matematika Diskrit 3/33

Hukum-Hukum Aljabar Himpunan Erwin Sitompul Matematika Diskrit 3/34

Latihan Contoh: Untuk diagram Venn berikut, yang menampilkan himpunan A, B, dan C di dalam himpunan semesta U, tentukan nomor-nomor yang sesuai dengan notasi simbolik aljabar himpunan berikut: 3, 4, 6, 7 h) A B a) A B 1, 2 i) (A – B) – C b) B C 1, 3 c) A C 1, 2, 3, 4, 5, 7 j) A – (B – C) k) (A B) C d) B A 4, 7 l) A (B C) e) A B C 1 f) (A B) C 2, 6, 7 m) (A B) – C g) (A B) – C 2, 6, 7 n) (A C) – B Erwin Sitompul 7 1, 4, 7 5, 6, 7 3, 4 4, 8 Matematika Diskrit 3/35

Pekerjaan Rumah (PR 3) Diberikan U = { 1, 2, 3, 4, 5, 6, 7, 8, 9 } sebagai sebuah himpunan semesta dan diberikan pula: A = { 1, 2, 3, 4, 5 }, B = { 4, 5, 6, 7 }, C = { 5, 6, 7, 8, 9 }, D = { 1, 3, 5, 7, 9 }, E = { 2, 4, 6, 8 }, F = { 1, 5, 9 }. Tentukanlah: a) A C b) A B c) A F d) (C D) E e) (F – C) – A Erwin Sitompul Matematika Diskrit 3/36