Pohon bagian ke 6 Matematika Diskrit 1 Definisi

Pohon (bagian ke 6) Matematika Diskrit 1

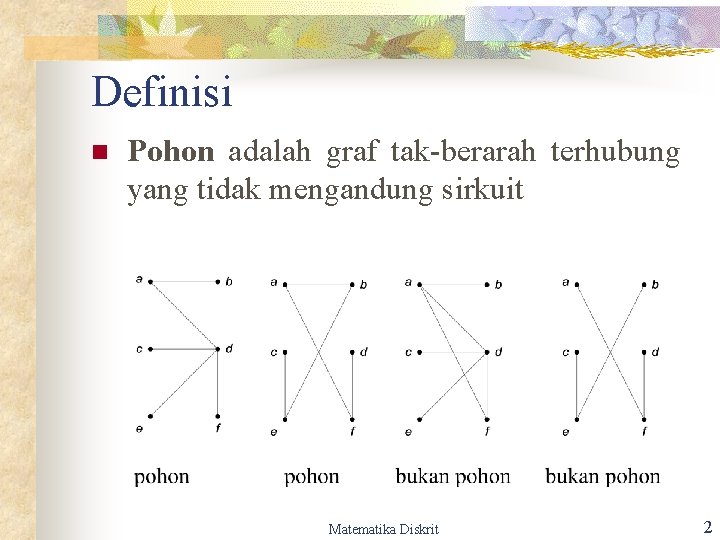
Definisi n Pohon adalah graf tak-berarah terhubung yang tidak mengandung sirkuit Matematika Diskrit 2

Matematika Diskrit 3

Sifat-sifat (properti) pohon Matematika Diskrit 4

Pohon Merentang (spanning tree) Matematika Diskrit 5

Matematika Diskrit 6

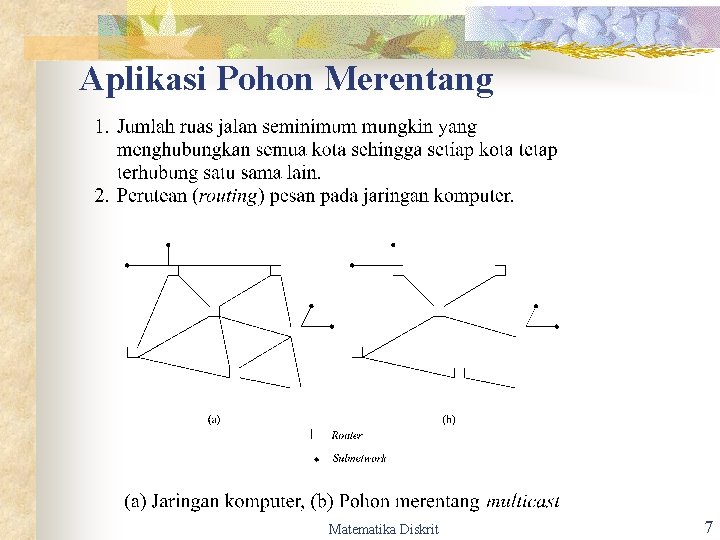
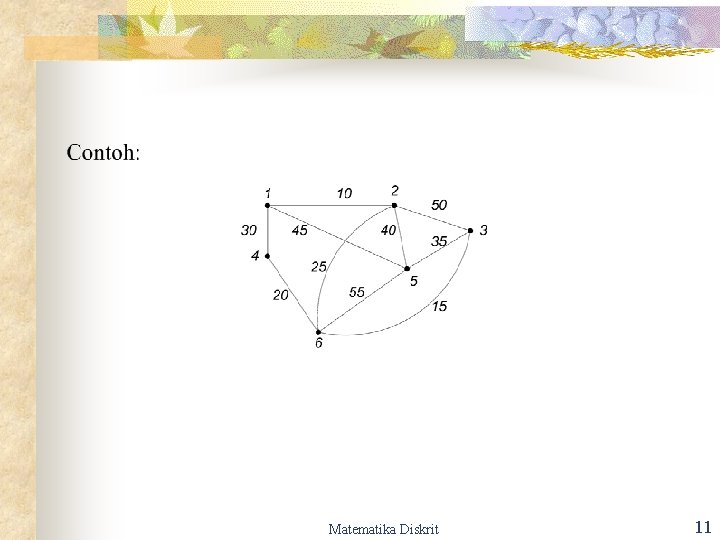
Aplikasi Pohon Merentang Matematika Diskrit 7

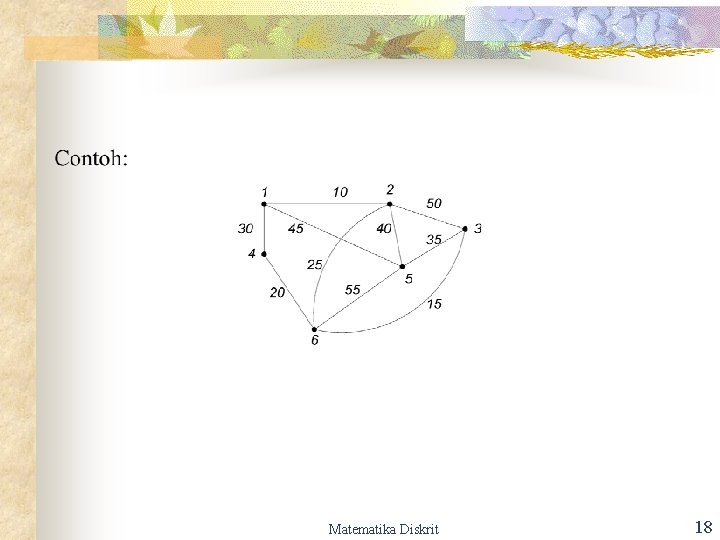
Pohon Merentang Minimum Matematika Diskrit 8

Matematika Diskrit 9

Matematika Diskrit 10

Matematika Diskrit 11

Matematika Diskrit 12

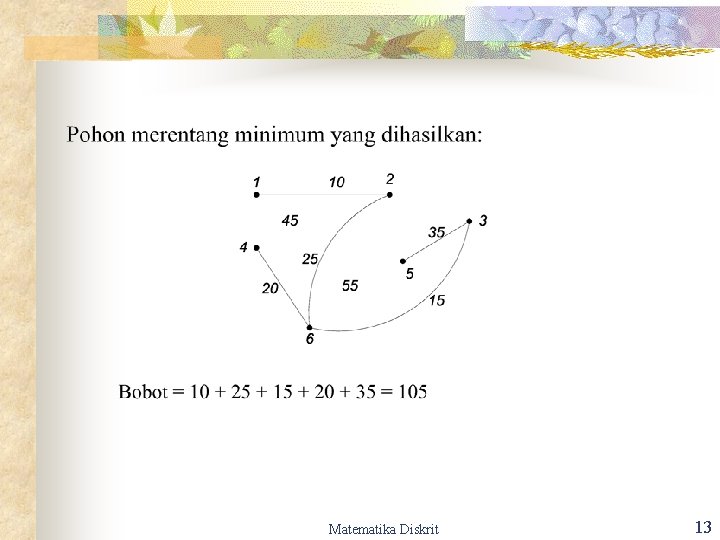
Matematika Diskrit 13

n Pohon merentang yang dihasilkan tidak selalu unik meskipun bobotnya tetap sama. n Hal ini terjadi jika ada beberapa sisi yang akan dipilih berbobot sama. Matematika Diskrit 14

Matematika Diskrit 15

Matematika Diskrit 16

Matematika Diskrit 17

Matematika Diskrit 18

Matematika Diskrit 19

Matematika Diskrit 20

Pohon berakar (rooted tree) Matematika Diskrit 21

Matematika Diskrit 22

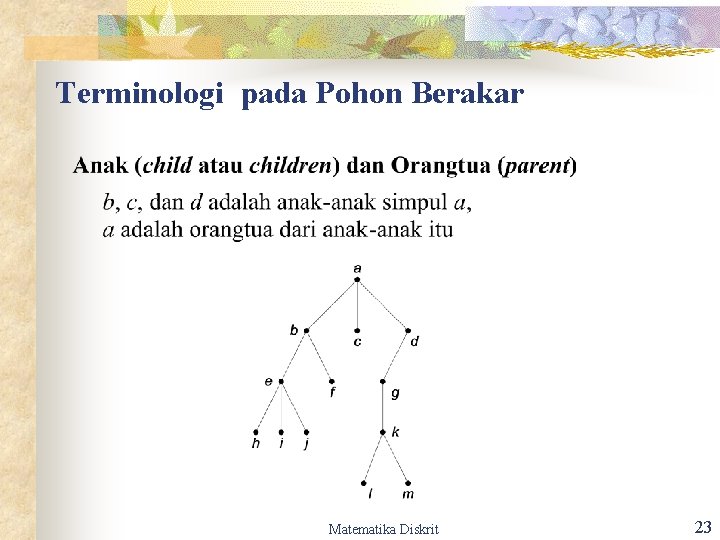
Terminologi pada Pohon Berakar Matematika Diskrit 23

Matematika Diskrit 24

Matematika Diskrit 25

Matematika Diskrit 26

Matematika Diskrit 27

Matematika Diskrit 28

Pohon Terurut (ordered tree) Matematika Diskrit 29

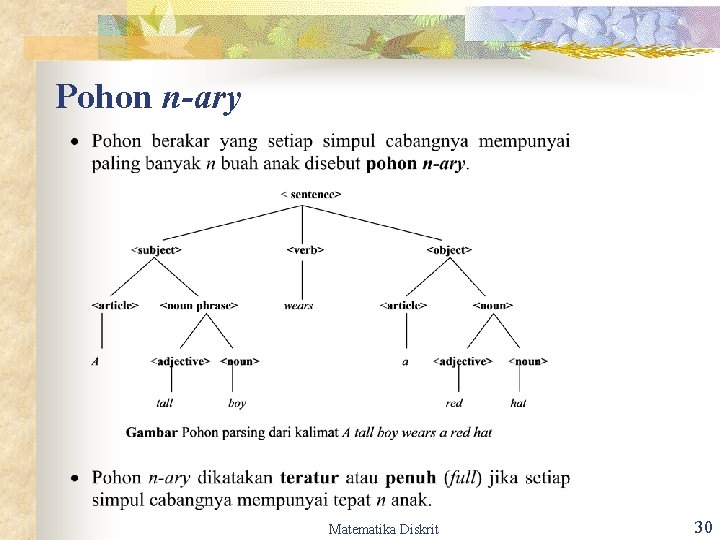
Pohon n-ary Matematika Diskrit 30

Pohon Biner (binary tree) n n n Adalah pohon n-ary dengan n = 2. Pohon yang paling penting karena banyak aplikasinya. Setiap simpul di adlam pohon biner mempunyai paling banyak 2 buah anak. Dibedakan antara anak kiri (left child) dan anak kanan (right child) Karena ada perbedaan urutan anak, maka pohon biner adalah pohon terurut. Matematika Diskrit 31

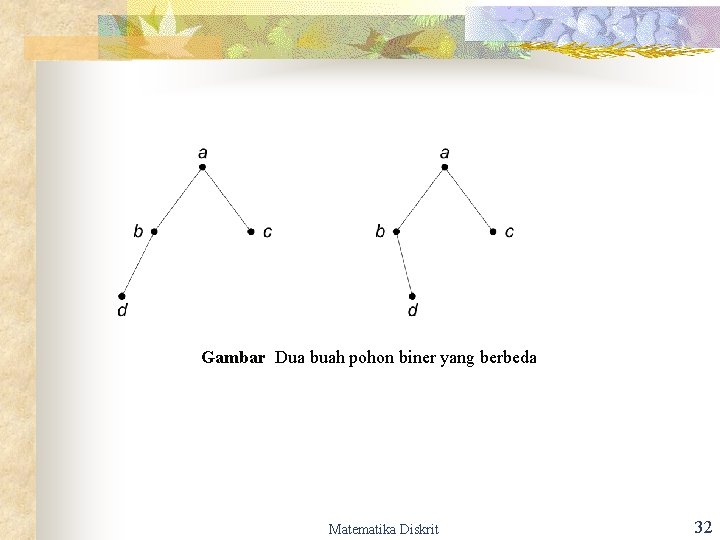
Gambar Dua buah pohon biner yang berbeda Matematika Diskrit 32

Matematika Diskrit 33

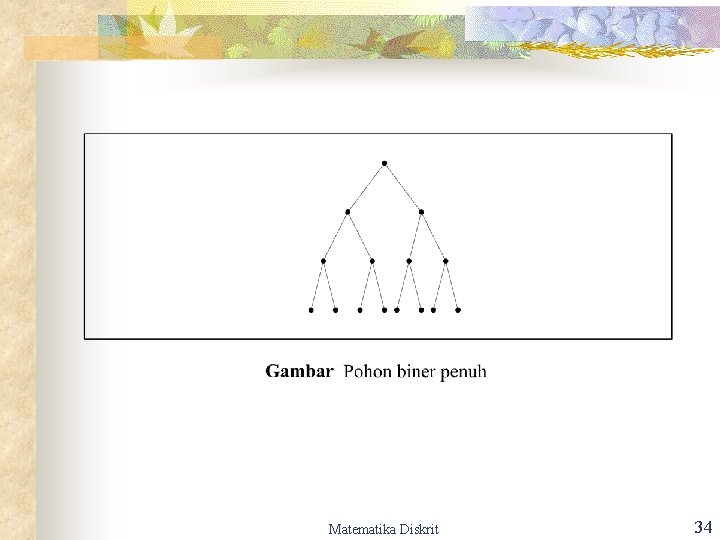
Matematika Diskrit 34

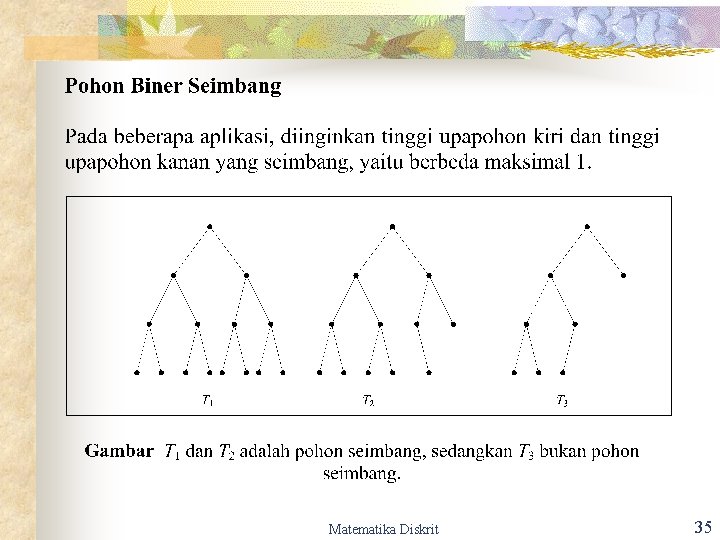
Matematika Diskrit 35

Terapan Pohon Biner daun operand simpul dalam operator Matematika Diskrit 36

Matematika Diskrit 37

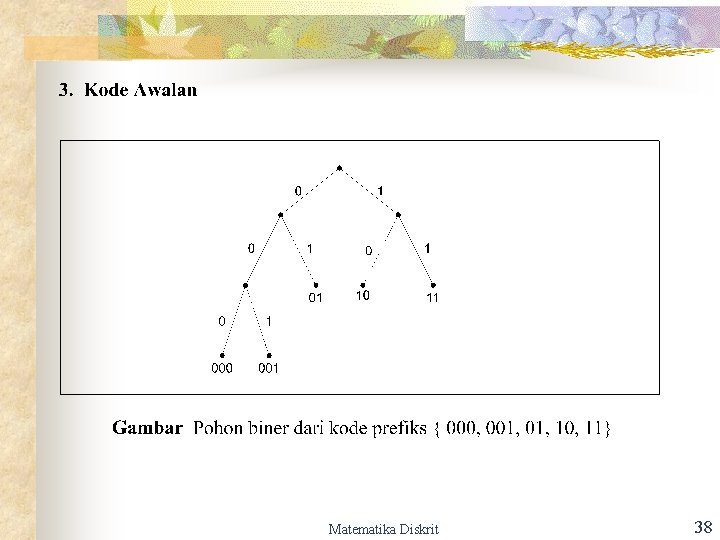
Matematika Diskrit 38

Matematika Diskrit 39

Matematika Diskrit 40

n Algoritma pembentukan pohon Huffman 1. Pilih dua simbol dengan peluang (probability) paling kecil (pada contoh di atas simbol B dan D). Kedua simbol tadi dikombinasikan sebagai simpul orangtua dari simbol B dan D sehingga menjadi simbol BD dengan peluang 1/7 + 1/7 = 2/7, yaitu jumlah peluang kedua anaknya. 2. Selanjutnya, pilih dua simbol berikutnya, termasuk simbol baru, yang mempunyai peluang terkecil. 3. Ulangi langkah 1 dan 2 sampai seluruh simbol habis. Matematika Diskrit 41

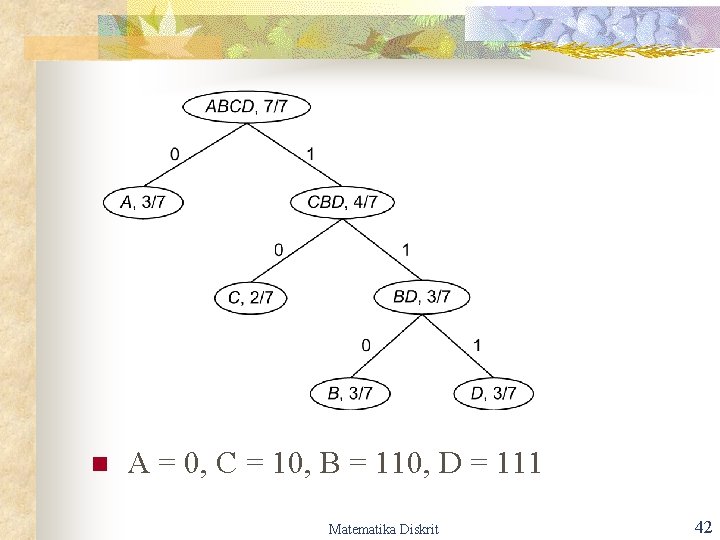
n A = 0, C = 10, B = 110, D = 111 Matematika Diskrit 42

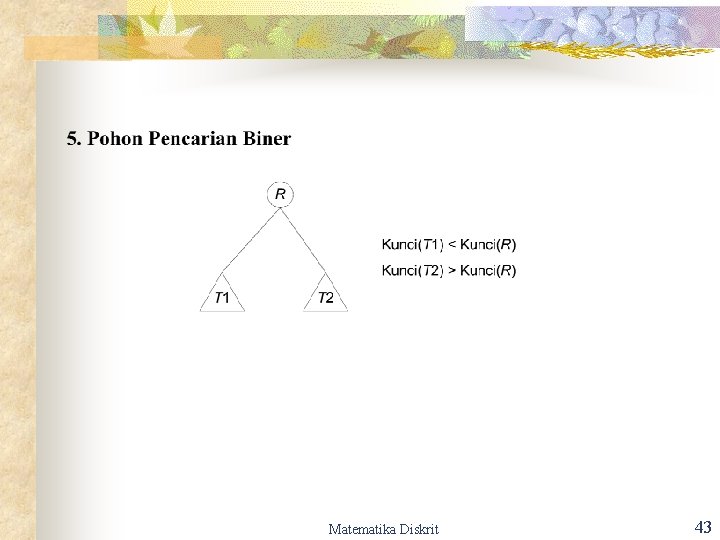
Matematika Diskrit 43

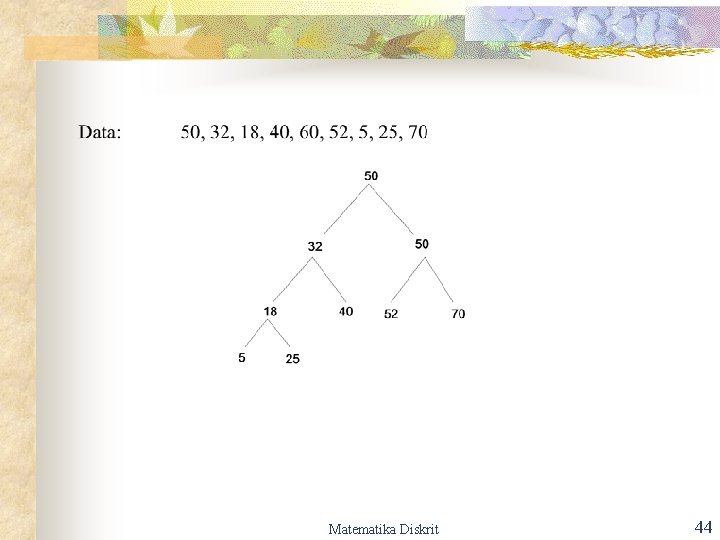
Matematika Diskrit 44

Penelusuran (traversal) Pohon Biner Matematika Diskrit 45

Matematika Diskrit 46

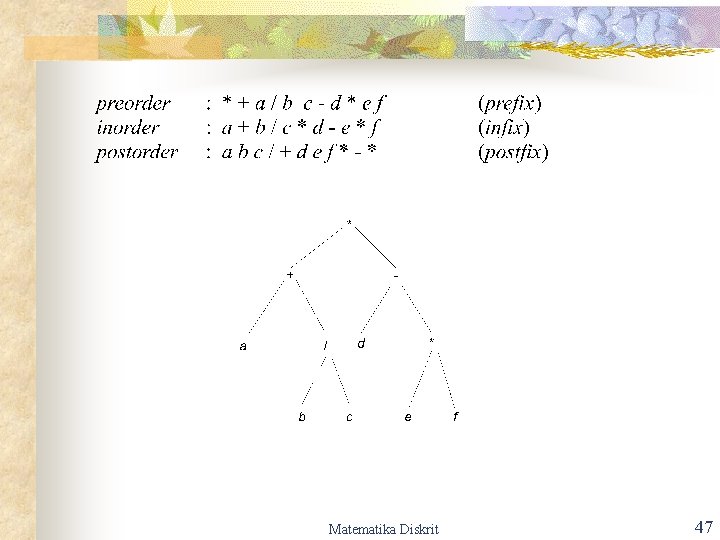
Matematika Diskrit 47

Soal latihan 1. Diketahui 8 buah koin uang logam. Satu dari delapan koin itu ternyata palsu. Koin yang palsu mungkin lebih ringan atau lebih berat daripada koin yang asli. Misalkan tersedia sebuah timbangan neraca yang sangat teliti. Buatlah pohon keputusan untuk mencari uang palsu dengan cara menimbang paling banyak hanya 3 kali saja. Matematika Diskrit 48

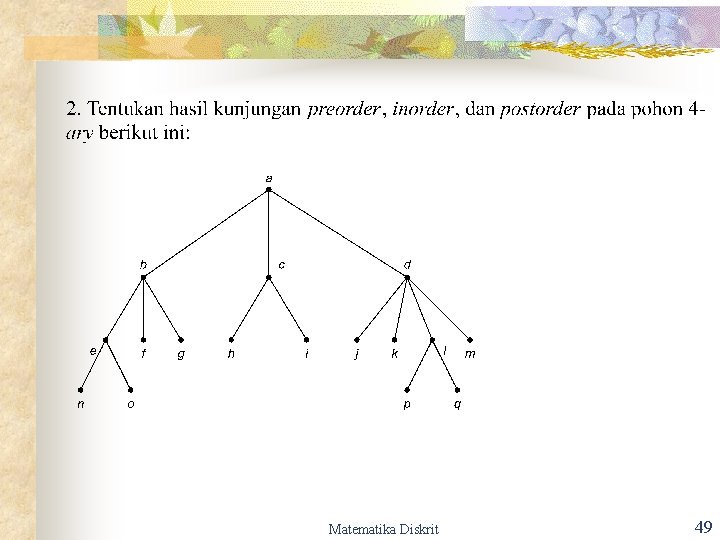
Matematika Diskrit 49

3. Gunakan pohon berakar untuk menggambarkan semua kemungkinan hasil dari pertandingan tenis antara dua orang pemain, Anton dan Budi, yang dalam hal ini pemenangnya adalah pemain yang pertama memenangkan dua set berturut atau pemain yang pertama memenangkan total tiga set. Matematika Diskrit 50

Matematika Diskrit 51

Matematika Diskrit 52