MATEMATIKA INFORMATIKA 2 LATTICE Definisi Sebuah lattice adalah

MATEMATIKA INFORMATIKA 2 LATTICE

Definisi: Sebuah lattice adalah sebuah poset (L, ≤) yang setiap himpunan bagiannya {a, b} memiliki dua elemen yaitu infimum dan supremum. Misalkan L ≠ ∅, yang tertutup terhadap dua operasi biner, yaitu ⋀ dan ⋁ (meet dan join). Maka L disebut LATTICE jika ∀ a, b, c ∈ L, memenuhi: a) Hukum komutatif a ∧ b = b ∧ a dan a ∨ b = b ∨ a b) Hukum Asosiatif (a ∧ b) ∧ c = a ∧ (b ∧ c) dan(a ∨ b) ∨ c = a ∨ (b ∨ c) c) Hukum Absorpsi a ∨ (a ∧ b) = a dan a ∧ (a ∨ b) = a Notasi Lattice : < L, ∧, ∨ > atau < L, ≤> atau L.

Definisi: Misalkan < L, ∧, ∨ > suatu Lattice dan M adalah subset tak kosong dari L. Maka, lattice < M, ∧, ∨ > adalah sublattice dari < L, ∧, ∨ > jika dan hanya jika M tertutup dibawah operasi ∧ dan ∨. Definisi: Suatu poset A disebut lattice jika dan hanya jika a ∧ b = infimum (a, b) dan a ∨ b= supremum (a, b) ada untuk setiap pasangan elemen a dan b dalam himpunan A.

Definisi: Jika tidak ada x ∈ L sedemikian sehingga a ≤ x dan x ≤ b ( tidak ada x diantara a dan b). Maka : a adalah predecessor immediate dari b dan b adalah succcessor immediate dari a

ELEMEN LATTICE Misalkan suatu lattice dimana 0 adalah elemen terkecil dari L dan I adalah elemen terbesar dari L. Jika a ∈ L, maka: a) a disebut meet irreducible jika: a = x ∧ y mengakibatkan a = x atau a = y. b) a disebut join irreducible jika: a = x∨ y mengakibatkan a = x atau a = y. c) a disebut atom jika: a adalah join irreducible dan a succcessor immediate dari 0. d) ā adalah komplemen dari a jika: a ∨ ā = I dan a ∧ ā = 0.

JENIS LATTICE a. L adalah Lattice Terbatas jika L mempunyai sebuah elemen terkecil dan sebuah elemen terbesar. b. L disebut Lattice Distributif jika untuk semua a, b, c ∈ L berlaku: a ∧ (b ∨ c) = (a ∧ b) ∨ (a ∧ c) a ∨ (b ∧ c) = (a ∨ b) ∧ (a ∨ c) c. L disebut Lattice Complemented jika L terbatas dan semua elemen di L mempunyai komplemen. d. L disebut Lattice Complete jika semua subset dari L memiliki supremum dan infimum.

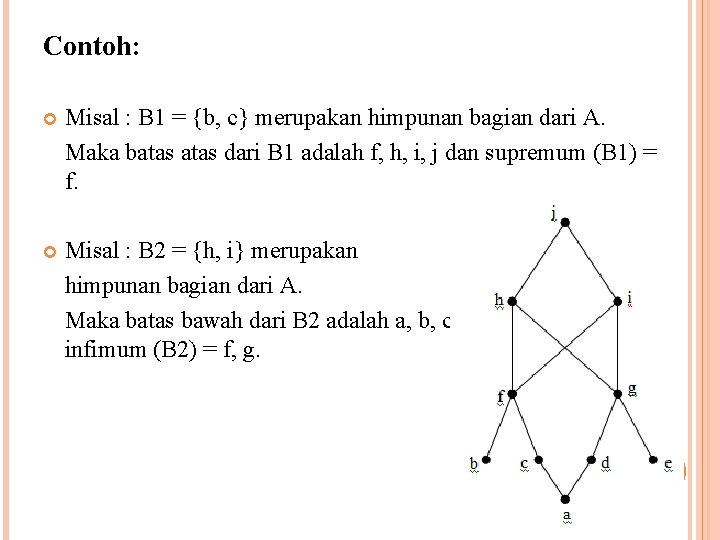
Contoh: Misal : B 1 = {b, c} merupakan himpunan bagian dari A. Maka batas dari B 1 adalah f, h, i, j dan supremum (B 1) = f. Misal : B 2 = {h, i} merupakan himpunan bagian dari A. Maka batas bawah dari B 2 adalah a, b, c, d, f dan g dan infimum (B 2) = f, g.

Contoh: Misalkan D 12= {1, 2, 3, 4, 6, 12} faktor-faktor dari 12 terurut oleh relasi pembagian adalah lattice dengan a ∨ b = KPK (a, b) dan a ∧ b = FPB (a, b). Maka: Elemen terkecil = 1 dan elemen terbesar = 12 Komplemen dari 4 adalah 3, karena 4 ∧ 3 = FPB (4, 3) = 1 dan 4 ∨ 3 = KPK (4, 3) = 12. Lattice D bukan merupakan lattice complemented karena 6 tidak mempunyai komplemen.

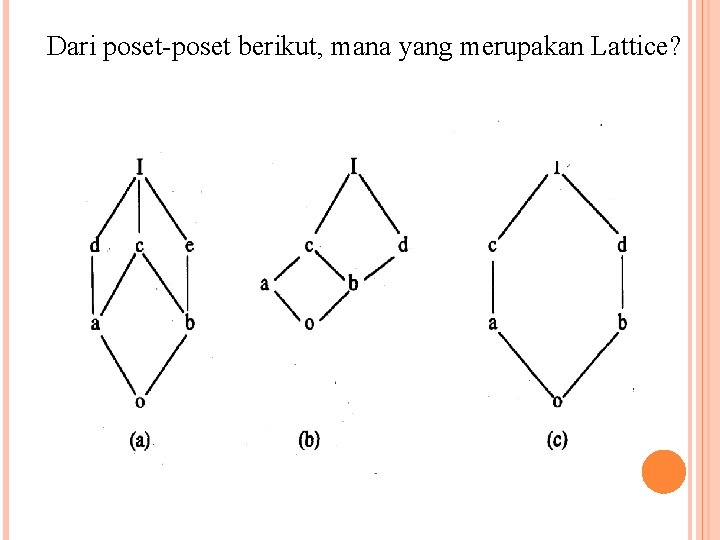
Dari poset-poset berikut, mana yang merupakan Lattice?