Tree Tree Pohon Dalam dunia nyata sebuah pohon

Tree

Tree (Pohon) • Dalam dunia nyata, sebuah pohon memiliki : akar, cabang, daun. • Dalam dunia komputer, pohon (tree) memiliki 3 (tiga) bagian tersebut namun dalam definisi yang lain.

Linear List dan Tree • Linear list digunakan untuk data yang terurut secara serial. – Contoh : nama mahasiswa satu kelas, nama hari dalam minggu, nama bulan dalam tahun, dll. • Tree digunakan untuk data yang terurut secara hirarki (one to many). – Contoh : tingkatan pegawai dalam perusahaan (direktor, manager, kepala divisi, dst), tingkatan class di Java, dll.

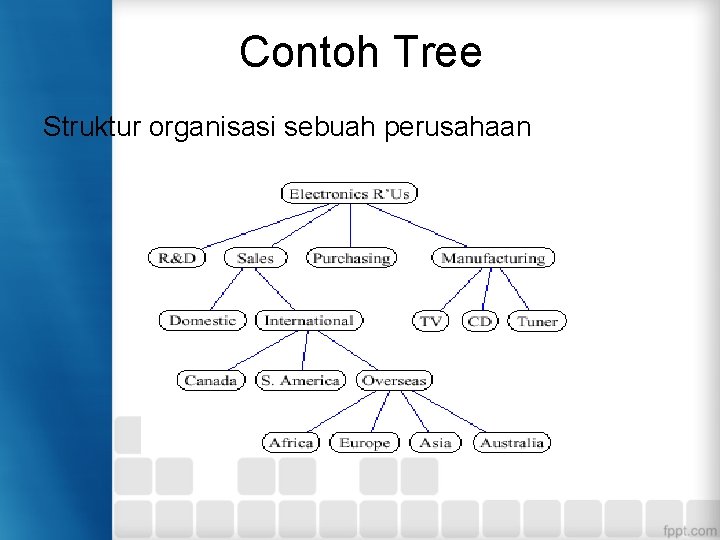
Contoh Tree Struktur organisasi sebuah perusahaan

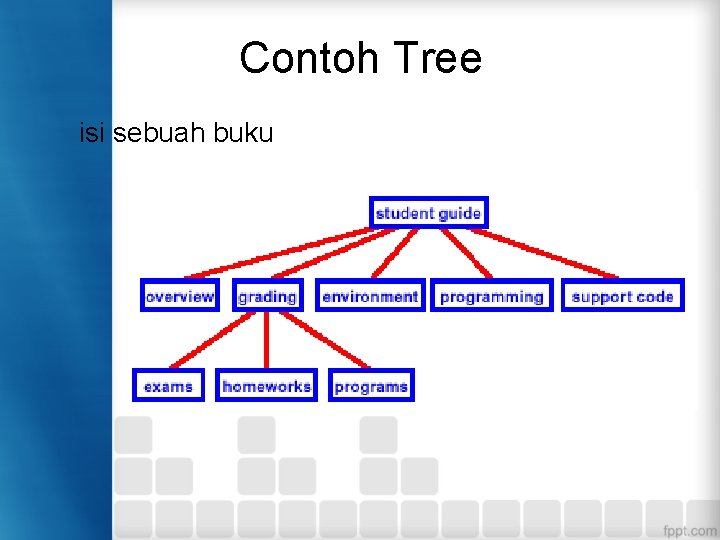
Contoh Tree isi sebuah buku

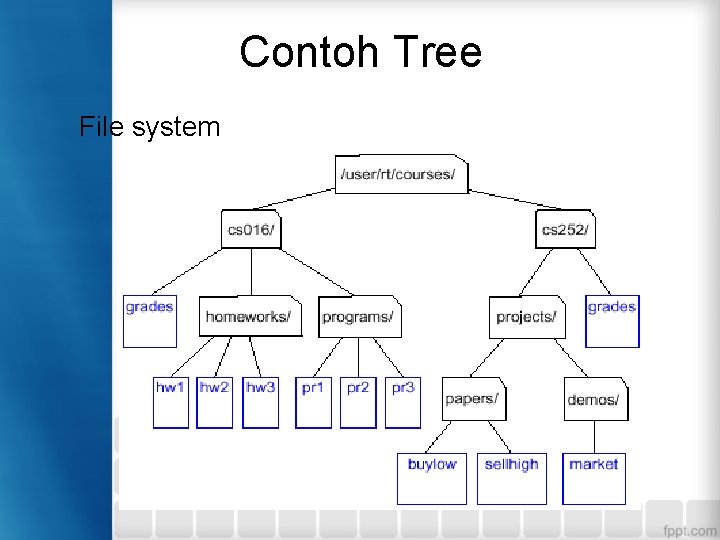
Contoh Tree File system

Definisi • Tree adalah Kumpulan element yang saling terhubung secara hirarki (one to many). • Element pada tree disebut node. Aturan : • Sebuah node hanya boleh memiliki satu induk/parent. Kecuali root, tidak memiliki induk/parent. • Setiap node dapat memiliki nol atau banyak cabang anak (one to many). • Node yang tidak memiliki cabang anak disebut daun.

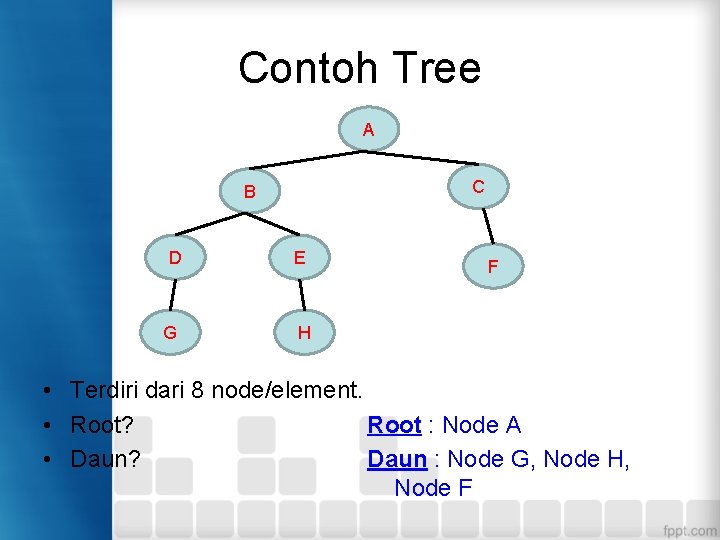
Contoh Tree A C B D E G H F • Terdiri dari 8 node/element. • Root? Root : Node A • Daun? Daun : Node G, Node H, Node F

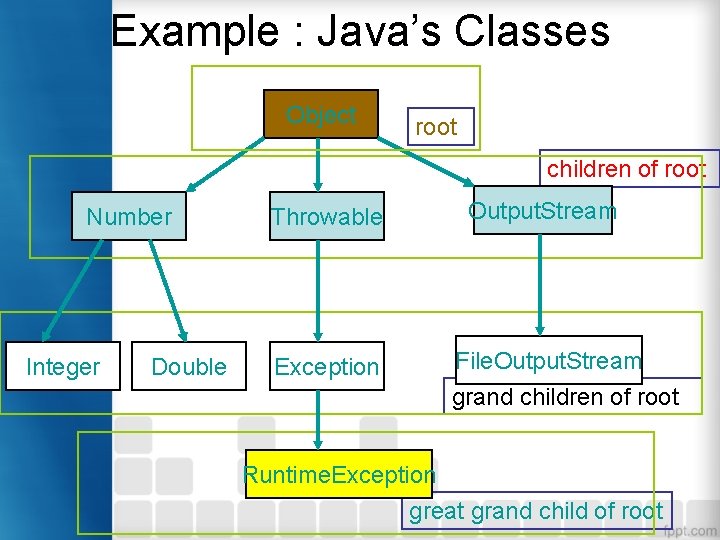
Example : Java’s Classes Object root children of root Number Integer Double Throwable Output. Stream Exception File. Output. Stream grand children of root Runtime. Exception great grand child of root

Root • Root (Node Root) adalah node yang memiliki hirarki tertinggi. • Node yang pertama kali dibentuk. Sehingga tidak memiliki parent (node induk). • Penelusuran path tiap node dimulai dari root. • Subtree adalah node-node lain dibawah root yang saling terhubung satu sama lain secara hirarki.

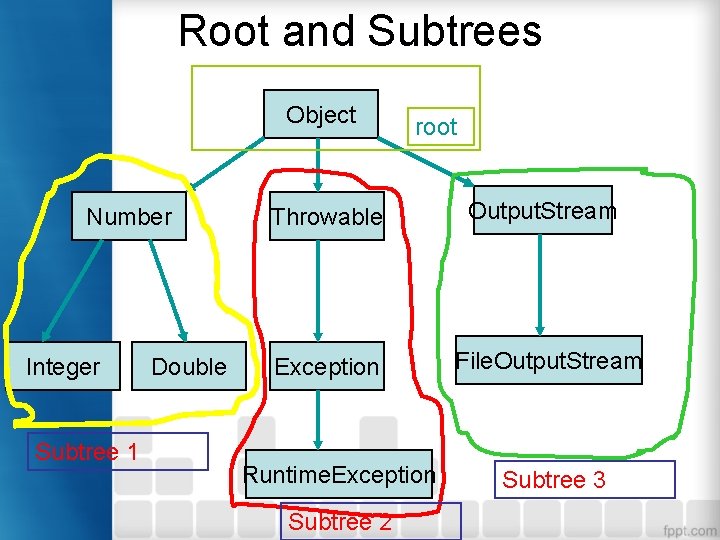
Root and Subtrees Object Number Integer Subtree 1 Double root Throwable Output. Stream Exception File. Output. Stream Runtime. Exception Subtree 2 Subtree 3

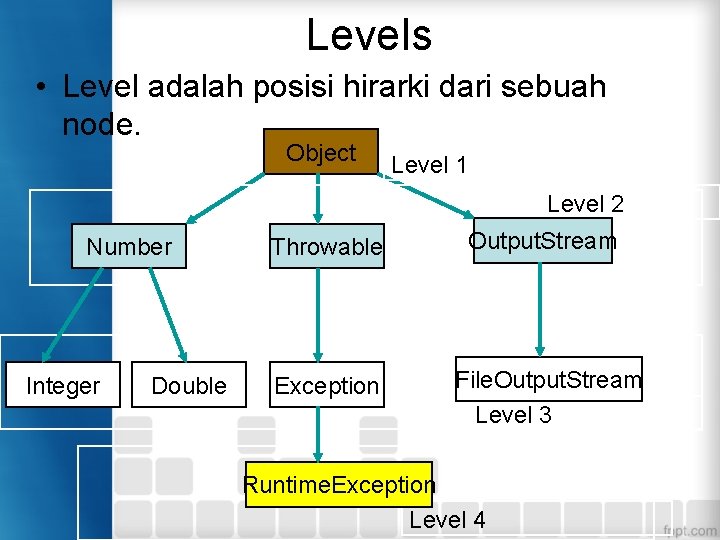
Levels • Level adalah posisi hirarki dari sebuah node. Object Level 1 Level 2 Number Integer Double Throwable Output. Stream Exception File. Output. Stream Level 3 Runtime. Exception Level 4

Istilah pada Tree

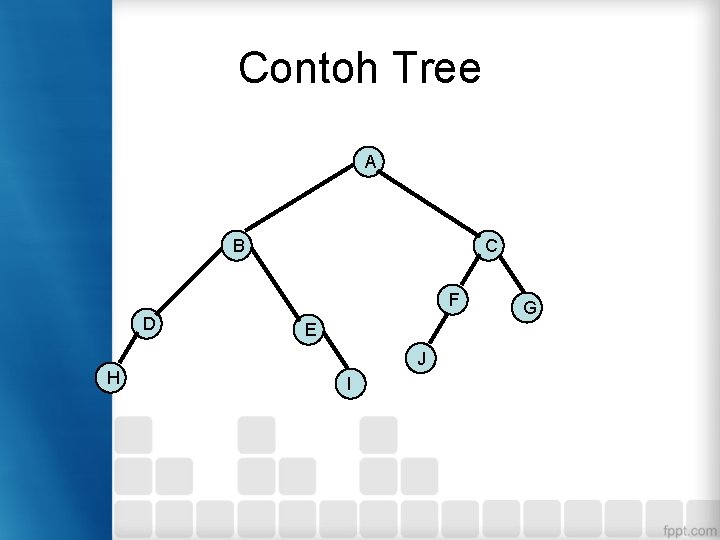
Contoh Tree A B C F D H E J I G

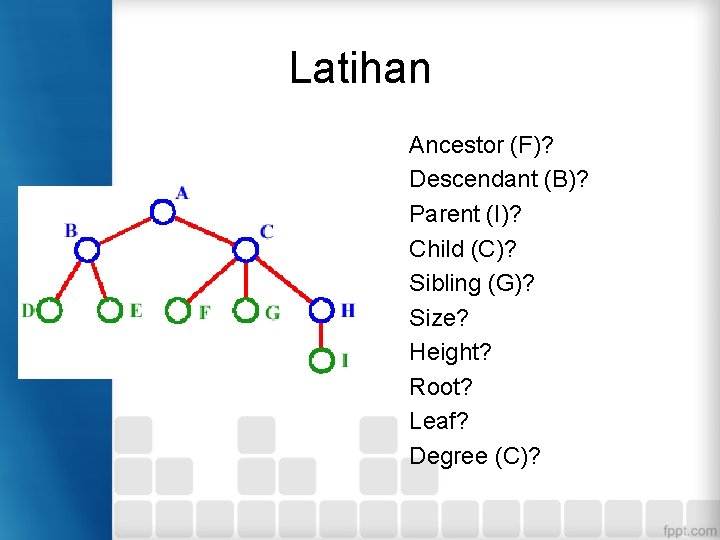
Latihan Ancestor (F)? Descendant (B)? Parent (I)? Child (C)? Sibling (G)? Size? Height? Root? Leaf? Degree (C)?

Latihan • Jawaban : Ancestor (F) = C, A Descendant (B) = D atau E Parent (I) = H Child (C) = F, G, H Sibling (G) = F, H Size = 9 Height = 4 Root = A Leaf = D, E, F, G, I Degree (C) = 3

Latihan Gambarkan tree dari representasi berikut: D F D B K J K L B A B C H D H K F E F G J I Tentukan : 1. Root 2. Leaf 3. Heigth 4. Child H 5. Parent A

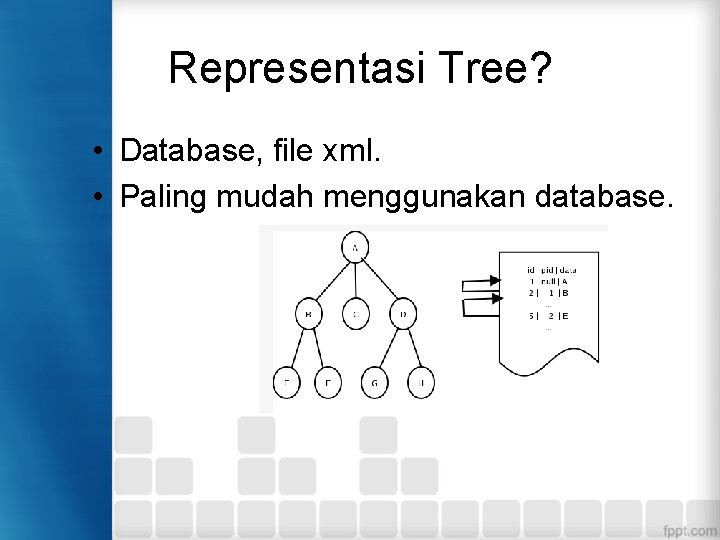
Representasi Tree? • Database, file xml. • Paling mudah menggunakan database.

Binary Tree

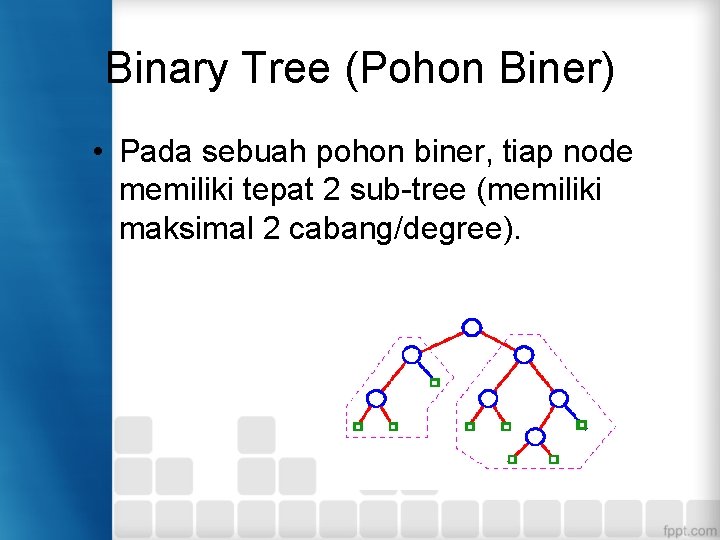
Binary Tree (Pohon Biner) • Pada sebuah pohon biner, tiap node memiliki tepat 2 sub-tree (memiliki maksimal 2 cabang/degree).

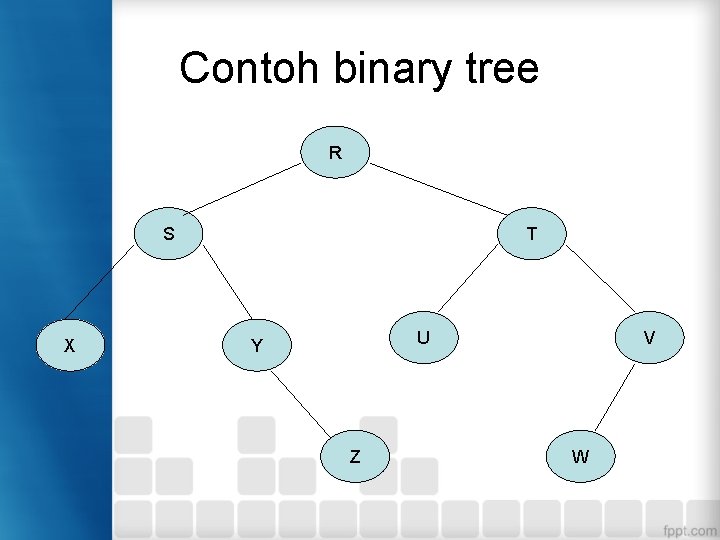
Contoh binary tree R S X T U Y Z V W

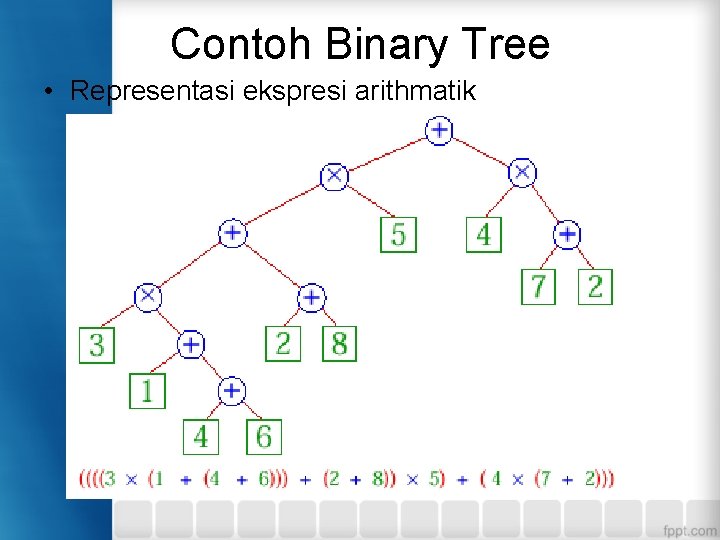
Contoh Binary Tree • Representasi ekspresi arithmatik

Latihan • Buatlah Binary tree dari ekspresi aritmatik berikut : (a + b) * (c – d) / (e + f)

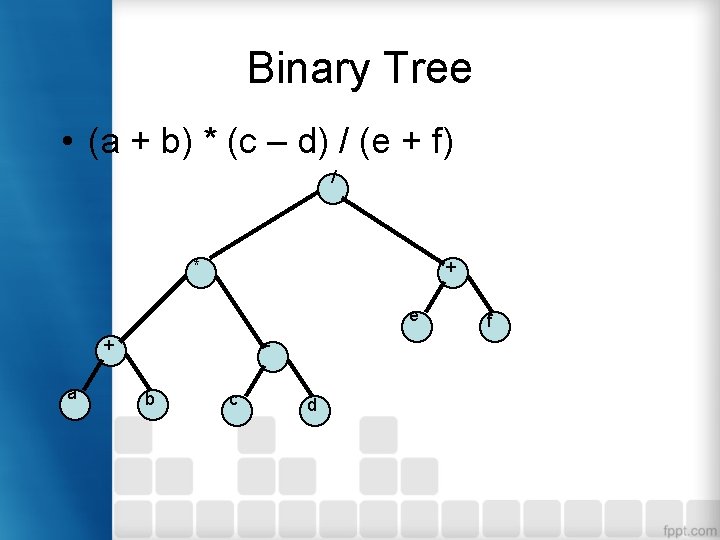
Binary Tree • (a + b) * (c – d) / (e + f) // * + e + a b c d f

Representasi Binary Tree • Binary tree dapat direpresentasikan dengan menggunakan array maupun linked list.

Akses Elemen • Posisi node dapat ditentukan berdasarkan rumus berikut : • Asumsi root dimulai dari index 0 : – Anak kiri dari node i berada pada indeks : 2*i+1 – Anak kanan dari node i berada pada indeks : 2*i+2 • Asumsi root dimulai dari index 1 : – Anak kiri dari node i berada pada indeks : 2*i – Anak kanan dari node i berada pada indeks : 2*i+1

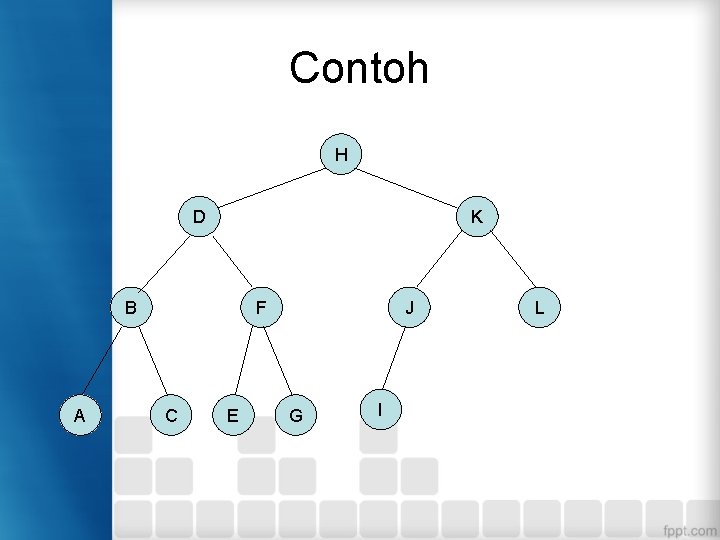
Contoh H D K B A F C E J G I L

Representasi Tree Representasi tree menggunakan array (asumsi root pada index 0) : H D K B F J L A C E G I 0 1 2 3 4 5 6 7 8 9 10 11 Representasi tree menggunakan array (asumsi root pada index 1): H 0 1 D 2 K B F J L A C E G I 3 4 5 6 7 8 9 10 11 12

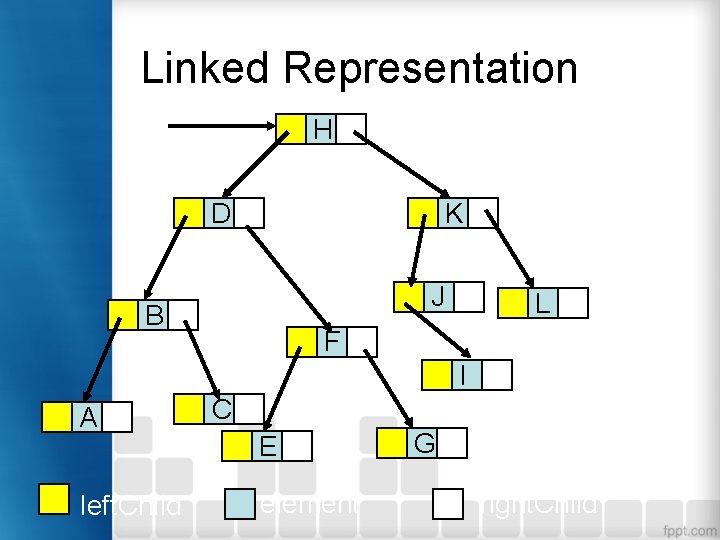
Linked Representation root H D K J B L F I A left. Child C E element G right. Child

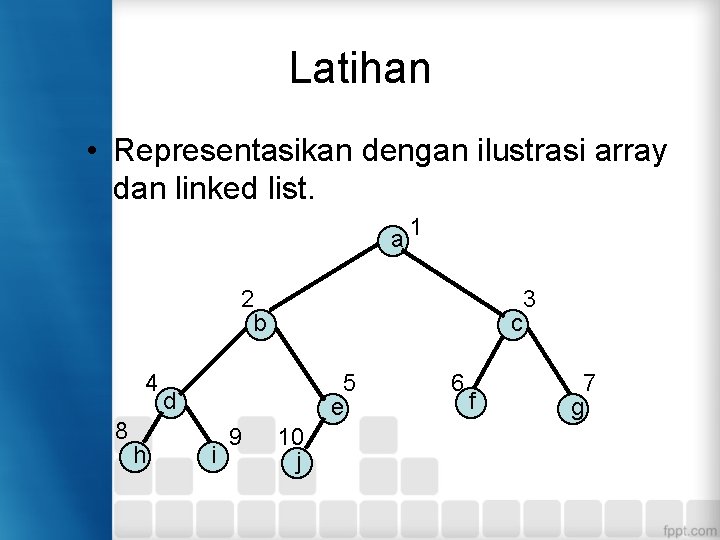
Latihan • Representasikan dengan ilustrasi array dan linked list. a 1 2 b 4 8 h c 5 e d i 9 10 j 6 f 3 7 g

Array Representation a 1 2 b 4 8 c 5 e d h tree[] i 9 6 3 7 g f 10 j a b c d e f g h i j 0 0 5 5 10 10

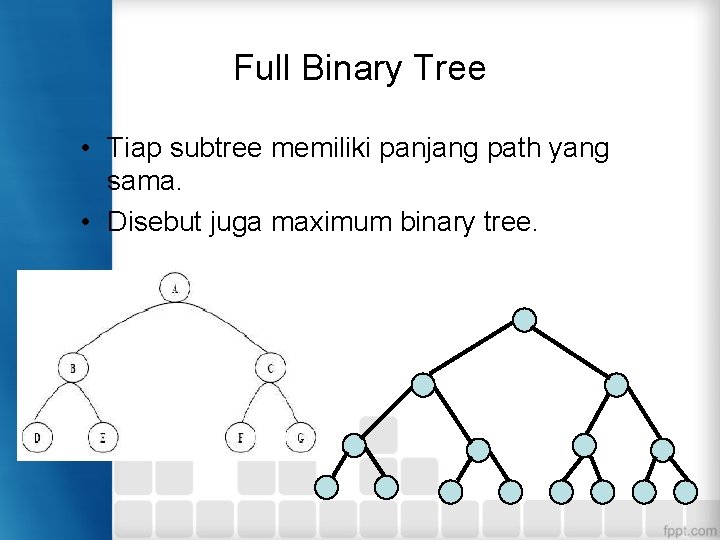
Full Binary Tree • Tiap subtree memiliki panjang path yang sama. • Disebut juga maximum binary tree.

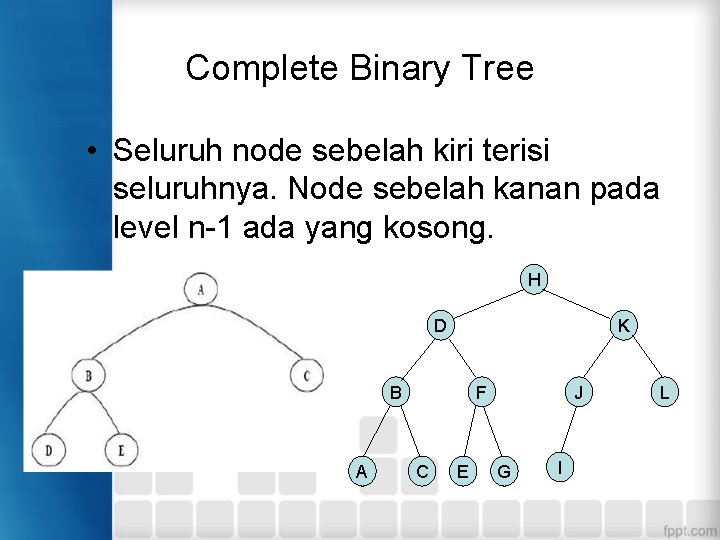
Complete Binary Tree • Seluruh node sebelah kiri terisi seluruhnya. Node sebelah kanan pada level n-1 ada yang kosong. H D K B A F C E J G I L

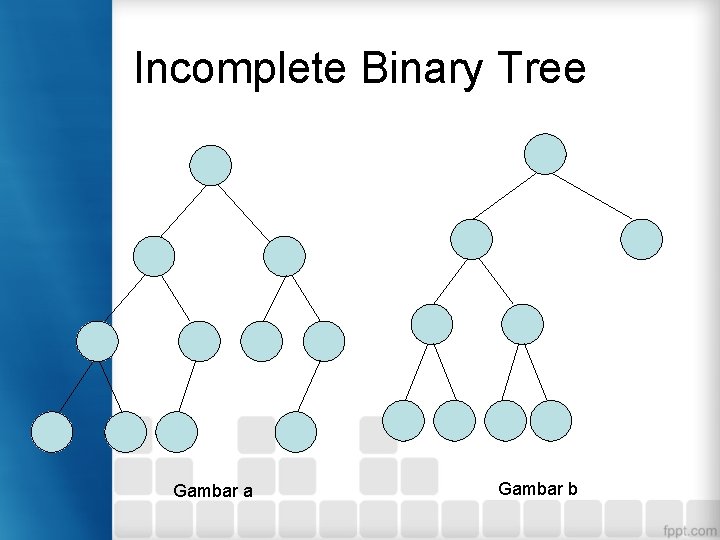
Incomplete Binary Tree Gambar a Gambar b

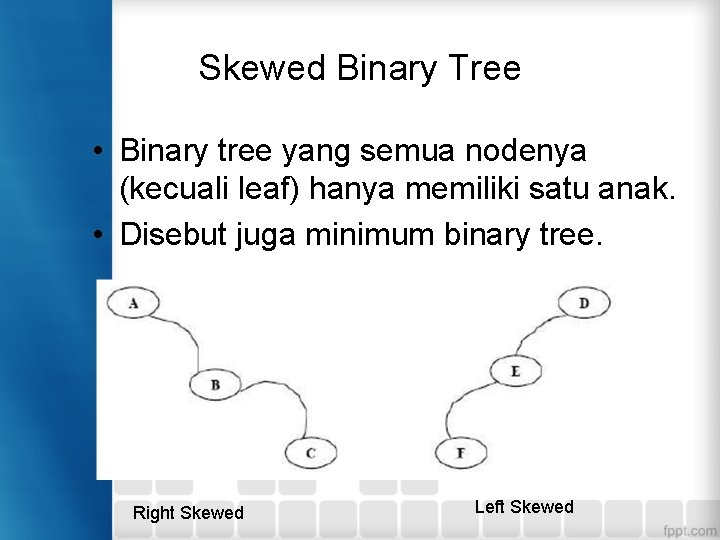
Skewed Binary Tree • Binary tree yang semua nodenya (kecuali leaf) hanya memiliki satu anak. • Disebut juga minimum binary tree. Right Skewed Left Skewed

Binary Tree Traversal

Definisi • Penelusuran seluruh node pada binary tree. • Metode : – Preorder – Inorder – Postorder – Level order

Pre. Order Traversal • Preorder traversal 1. Cetak data pada root 2. Secara rekursif mencetak seluruh data pada subpohon kiri 3. Secara rekursif mencetak seluruh data pada subpohon kanan

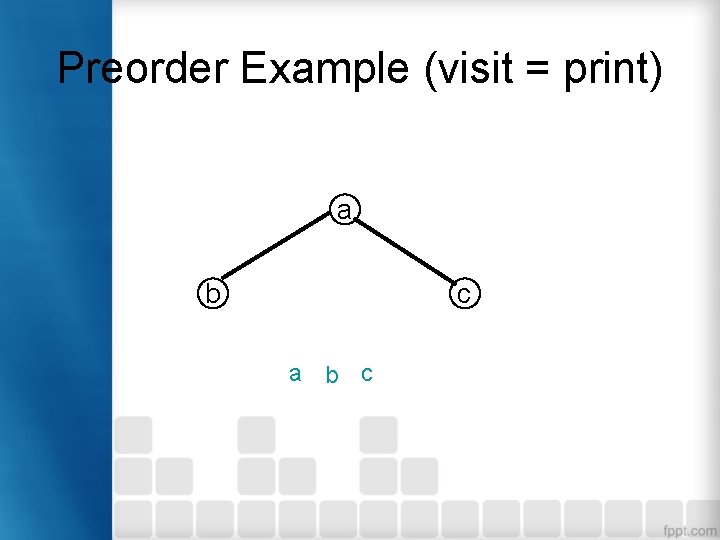
Preorder Example (visit = print) a b c

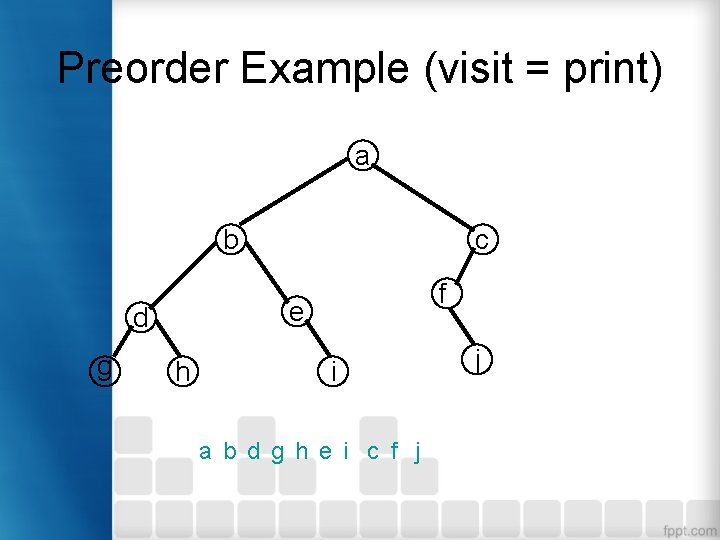
Preorder Example (visit = print) a b f e d g c h i a b d g h e i c f j j

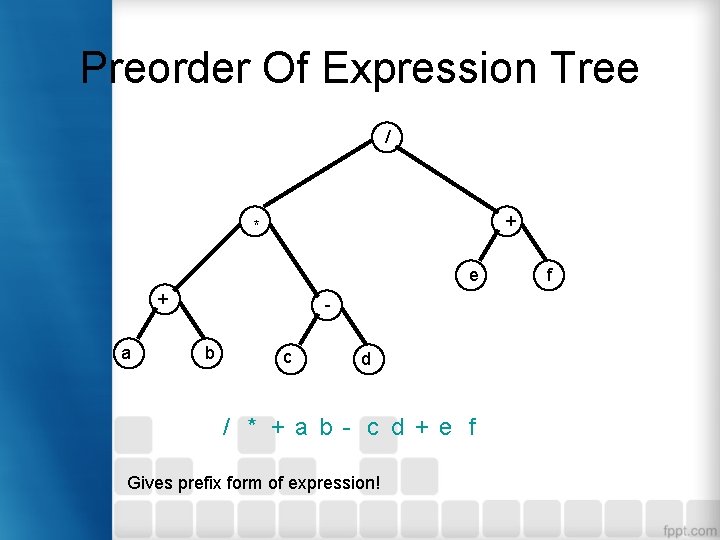
Preorder Of Expression Tree / + * e + a b c d / * + a b - c d + e f Gives prefix form of expression! f

In. Order Traversal • Inorder traversal 1. Secara rekursif mencetak seluruh data pada subpohon kiri 2. Cetak data pada root 3. Secara rekursif mencetak seluruh data pada subpohon kanan

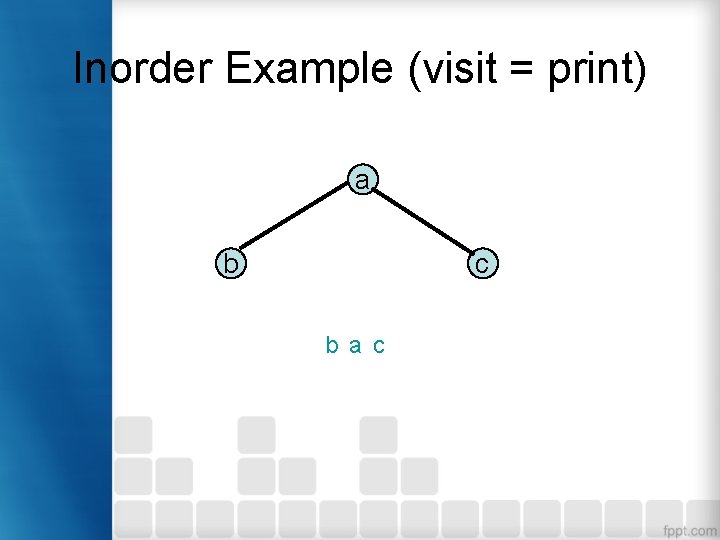
Inorder Example (visit = print) a b c b a c

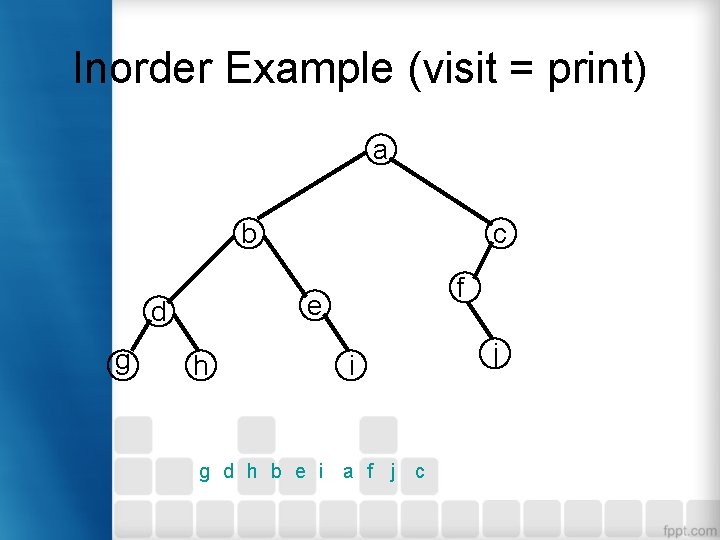
Inorder Example (visit = print) a b f e d g c h i g d h b e i a f j c j

Postorder Traversal • Postorder traversal 1. Secara rekursif mencetak seluruh data pada subpohon kiri 2. Secara rekursif mencetak seluruh data pada subpohon kanan 3. Cetak data pada root

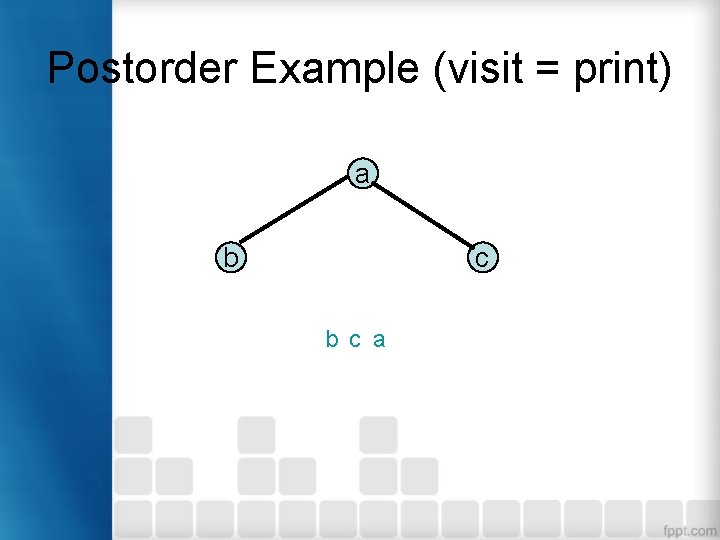
Postorder Example (visit = print) a b c a

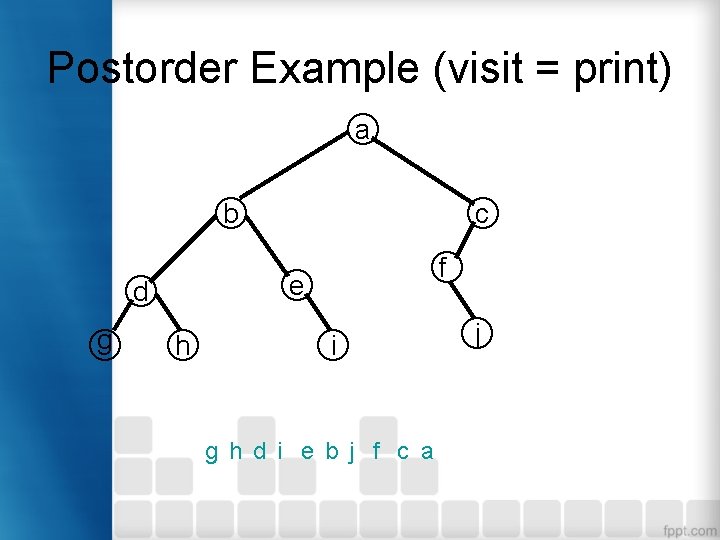
Postorder Example (visit = print) a b f e d g c h i g h d i e b j f c a j

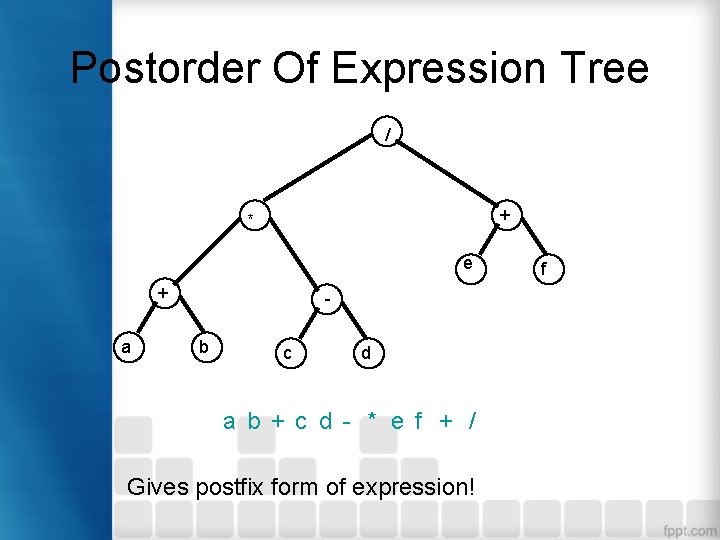
Postorder Of Expression Tree / + * e + a b c d a b + c d - * e f + / Gives postfix form of expression! f

Level Order • Secara rekursif mencetak data mulai dari level tertinggi

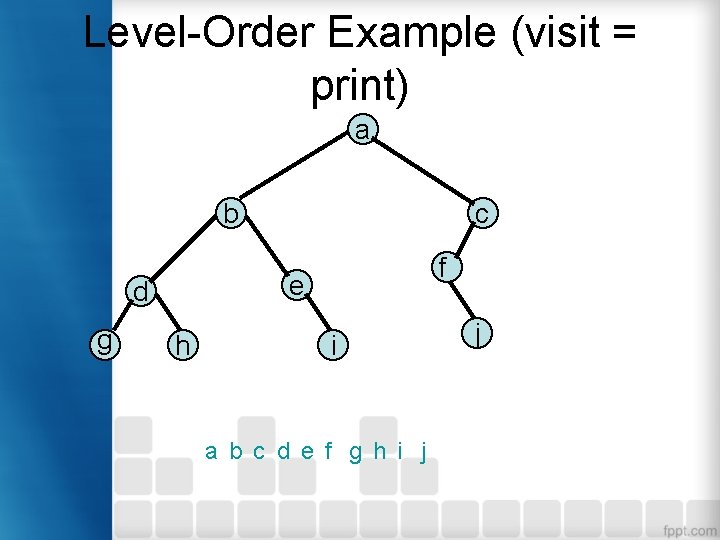
Level-Order Example (visit = print) a b f e d g c h i a b c d e f g h i j j

Latihan • Telusuri pohon biner berikut dengan menggunakan metode pre, in, post, dan level traversal.

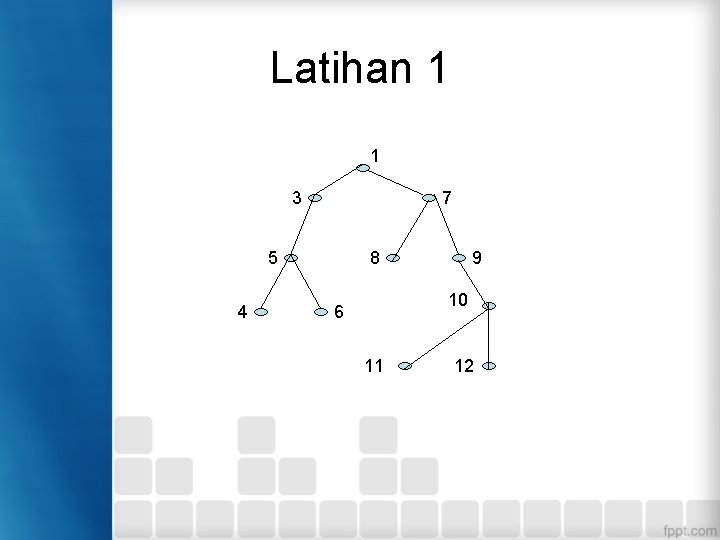
Latihan 1 1 3 7 5 4 8 9 10 6 11 12

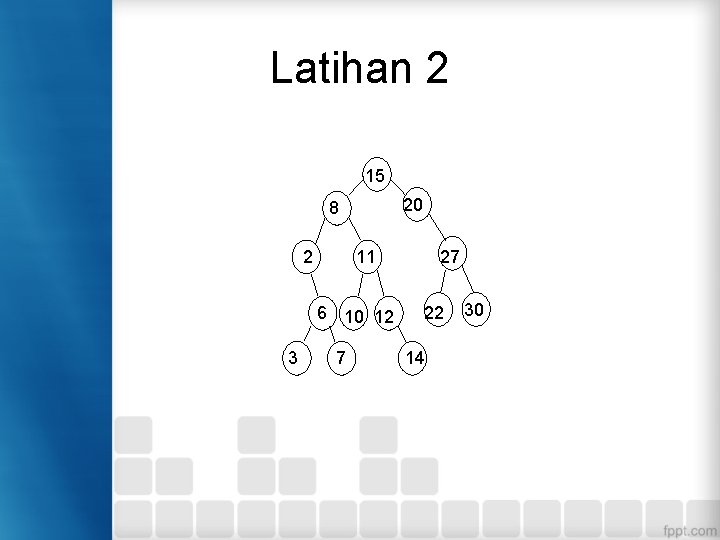
Latihan 2 15 20 8 6 10 12 3 27 11 2 7 22 14 30