Kuliah 4 2 HIMPUNAN Matematika Diskrit Dr Ing

Kuliah 4 2. HIMPUNAN Matematika Diskrit Dr. -Ing. Erwin Sitompul http: //zitompul. wordpress. com

Pekerjaan Rumah (PR 3) Diberikan U = { 1, 2, 3, 4, 5, 6, 7, 8, 9 } sebagai sebuah himpunan semesta dan diberikan pula: A = { 1, 2, 3, 4, 5 }, B = { 4, 5, 6, 7 }, C = { 5, 6, 7, 8, 9 }, D = { 1, 3, 5, 7, 9 }, E = { 2, 4, 6, 8 }, F = { 1, 5, 9 }. Tentukanlah: a) A C b) A B c) A F d) (C D) E e) (F – C) – A Erwin Sitompul Matematika Diskrit 4/2

Solusi Pekerjaan Rumah (PR 3) Erwin Sitompul Matematika Diskrit 4/3

Prinsip Dualitas dikatakan berlaku pada saat dua konsep yang berbeda dapat saling dipertukarkan namun tetap memberikan jawaban yang benar. Erwin Sitompul Matematika Diskrit 4/4

Prinsip Dualitas Contoh: Di Amerika Serikat kemudi mobil terletak di depan kiri. Di Inggris kemudi mobil terletak di depan kanan. Peraturan: Di Amerika Serikat: • Mobil harus berjalan di bagian kanan jalan. • Lajur kiri digunakan untuk mendahului. • Pada lampu lalu lintas, belok kanan jalan terus. Di Inggris: • Mobil harus berjalan di bagian kiri jalan. • Lajur kanan digunakan untuk mendahului. • Pada lampu lalu lintas, belok kiri jalan terus. Dalam hal ini berlalu Prinsip Dualitas: Konsep kiri dan kanan dapat dipertukarkan pada kedua negara tersebut sehingga peraturan yang berlaku di Amerika Serikat menjadi berlaku pula di Inggris, dan demikian juga sebaliknya. Erwin Sitompul Matematika Diskrit 4/5

Prinsip Dualitas pada Himpunan Misalkan S adalah suatu kesamaan (identity) yang melibatkan himpunan dan operasi-operasi seperti irisan, gabungan, komplemen, selisih, dan selisih simetris. Jika S* diperoleh dari S dengan mengganti U U sementara komplemen dibiarkan tetap seperti semula, maka kesamaan S* juga akan benar dan disebut dual dari S. Erwin Sitompul Matematika Diskrit 4/6

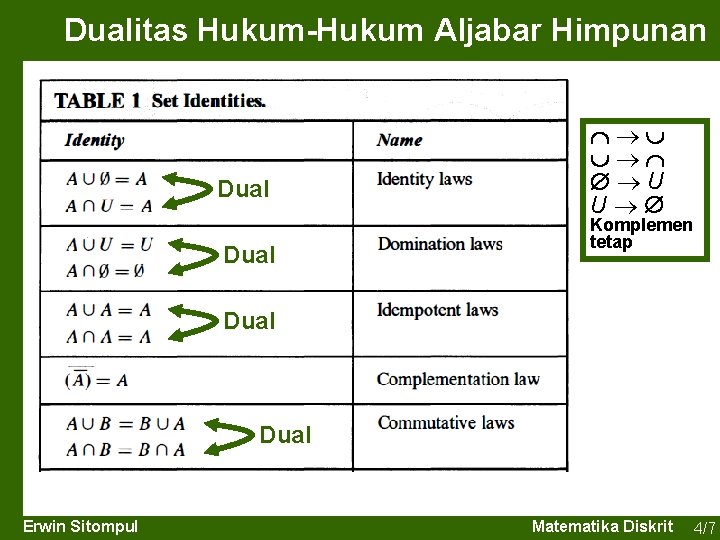
Dualitas Hukum-Hukum Aljabar Himpunan Dual U U Komplemen tetap Dual Erwin Sitompul Matematika Diskrit 4/7

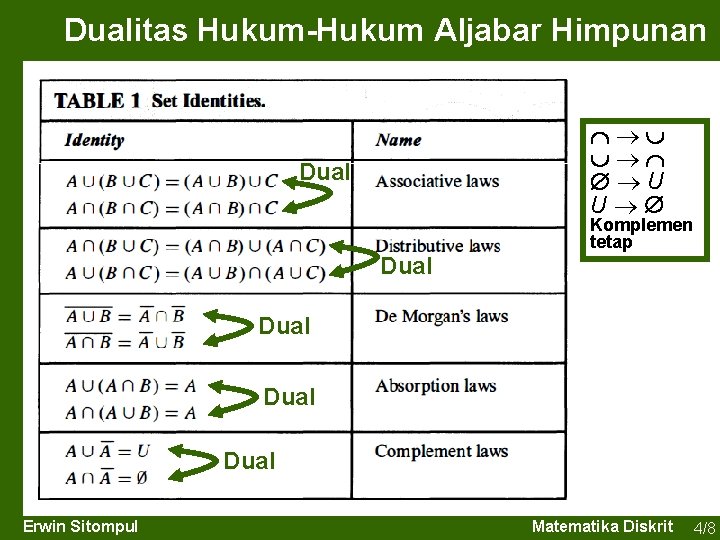
Dualitas Hukum-Hukum Aljabar Himpunan U U Dual Komplemen tetap Dual Erwin Sitompul Matematika Diskrit 4/8

Prinsip Dualitas pada Himpunan Contoh: Dual dari (A B) = A adalah: (A B) = A Erwin Sitompul Matematika Diskrit 4/9

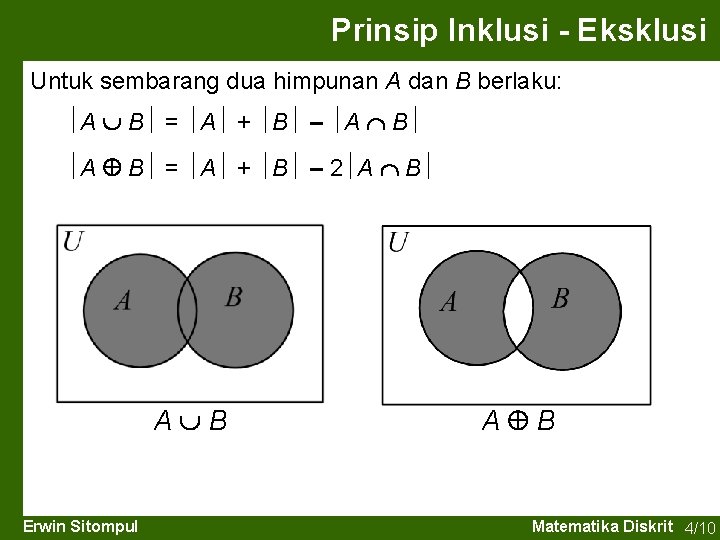
Prinsip Inklusi - Eksklusi Untuk sembarang dua himpunan A dan B berlaku: A B = A + B – 2 A B A B Erwin Sitompul A B Matematika Diskrit 4/10

Prinsip Inklusi - Eksklusi Contoh: Pada suatu angket yang diikuti 40 pelajar diketahui bahwa 32 orang lebih menyukai Internet Explorer, 18 orang lebih menyukai Mozilla Firefox, dan 2 orang tidak menyukai keduanya. Tentukanlah: a) Jumlah pelajar yang menyukai Internet Explorer atau Mozilla Firefox. b) Jumlah pelajar yang menyukai Internet Explorer atau Mozilla Firefox, tetapi tidak keduanya. Solusi: Misalkan U = { Jumlah keseluruhan pelajar yang mengikuti angket } A = { Jumlah pelajar yang lebih menyukai Internet Explorer } B = { Jumlah pelajar yang lebih menyukai Mozilla Firefox } Maka U = 40, A = 32, B = 18, A B = 2 Erwin Sitompul Matematika Diskrit 4/11

Prinsip Inklusi - Eksklusi a) Jumlah pelajar yang menyukai Internet Explorer atau Mozilla Firefox. A B A B = U – A B = 40 – 2 = 38 b) Jumlah pelajar yang menyukai Internet Explorer atau Mozilla Firefox, tetapi tidak keduanya. A B A B = A + B – A B = 32 + 18 – 38 = 12 A B = A + B – 2 A B = 32 + 18 – 2 12 = 26 Erwin Sitompul Matematika Diskrit 4/12

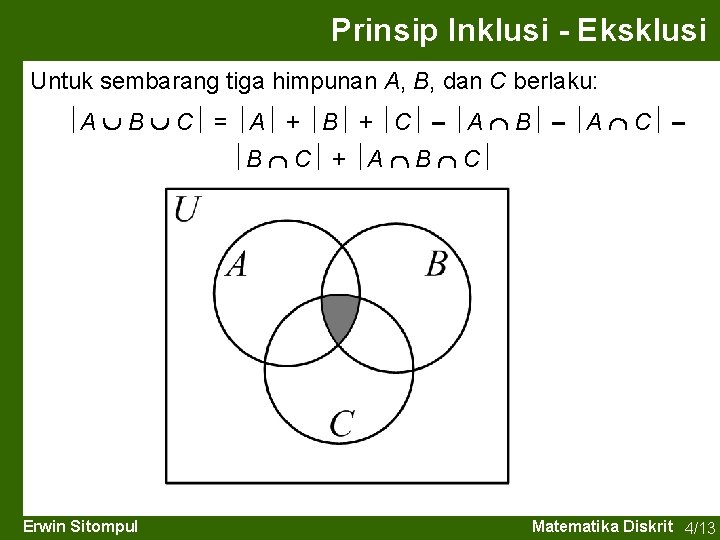
Prinsip Inklusi - Eksklusi Untuk sembarang tiga himpunan A, B, dan C berlaku: A B C = A + B + C – A B – A C – B C + A B C Erwin Sitompul Matematika Diskrit 4/13

Prinsip Inklusi - Eksklusi Contoh: Di antara bilangan bulat antara 101 dan 600 (termasuk 101 dan 600 itu sendiri), berapa banyak bilangan yang tidak habis dibagi oleh 4 dan 5 atau yang habis dibagi oleh keduanya? Solusi: Misalkan U={ Jumlah bilangan bulat antara 101 dan 600, termasuk 101 dan 600 } A = { Anggota U yang habis dibagi 4 } B = { Anggota U yang habis dibagi 5 } Maka U = 500 Ditanyakan: A B ? A = 500/4 = 125 B = 500/5 = 100 A B = 500/20 = 25 p q (p q) ~(p q) (~p ~q) (p q) Erwin Sitompul Matematika Diskrit 4/14

Prinsip Inklusi - Eksklusi U = 500 A = 500/4 = 125 B = 500/5 = 100 A B = 500/20 = 25 A B = A + B – 2 A B = 125 + 100 – 2 25 = 175 A B = U – A B = 500 – 175 = 325 Erwin Sitompul Matematika Diskrit 4/15

Pembuktian pada Proposisi Himpunan adalah argumen yang mempergunakan notasi himpunan. Proposisi yang akan dibuktikan umumnya berbentuk kesamaan (identity). Contoh: Buktikan bahwa “A (B C) = (A B) (A C). ” Pembuktian pada proposisi himpunan dapat dilakukan dengan 2 cara: 1. Menggunakan tabel keanggotaan. 2. Menggunakan hukum-hukum aljabar himpunan. Erwin Sitompul Matematika Diskrit 4/16

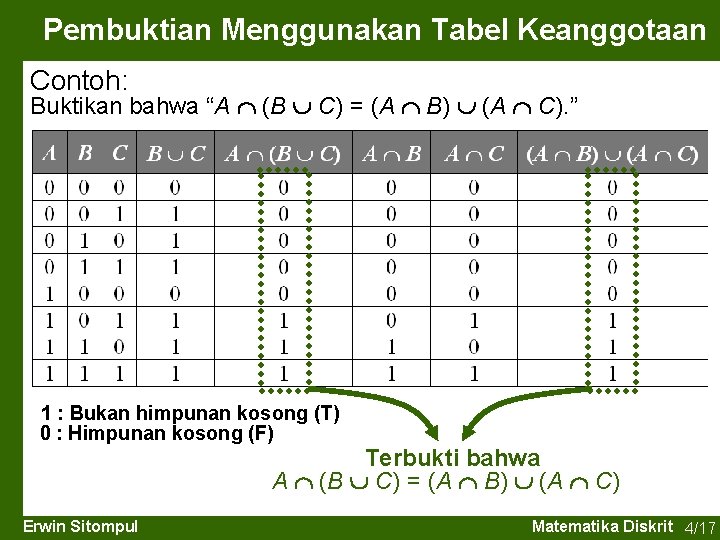
Pembuktian Menggunakan Tabel Keanggotaan Contoh: Buktikan bahwa “A (B C) = (A B) (A C). ” 1 : Bukan himpunan kosong (T) 0 : Himpunan kosong (F) Terbukti bahwa A (B C) = (A B) (A C) Erwin Sitompul Matematika Diskrit 4/17

Pembuktian Menggunakan Hukum-Hukum Aljabar Himpunan Contoh: Buktikan bahwa “(A B) = A. ” Solusi: (A B) = A (B B) =A U =A Hk. Distributif Hk. Komplemen Hk. Identitas Contoh: Buktikan bahwa “A (B – A) = (A B). ” Solusi: A (B – A) = A (B A) = (A B) (A A) = (A B) U =A B Erwin Sitompul Def. Operasi Selisih Hk. Distributif Hk. Komplemen Hk. Identitas Matematika Diskrit 4/18

Pekerjaan Rumah (PR 4) Buktikan bahwa untuk sembarang himpunan A dan B berlaku: a) A (A B) = A B b) A (A B) = A B Erwin Sitompul Matematika Diskrit 4/19