Predicate Logic Goal of Logic The goal of





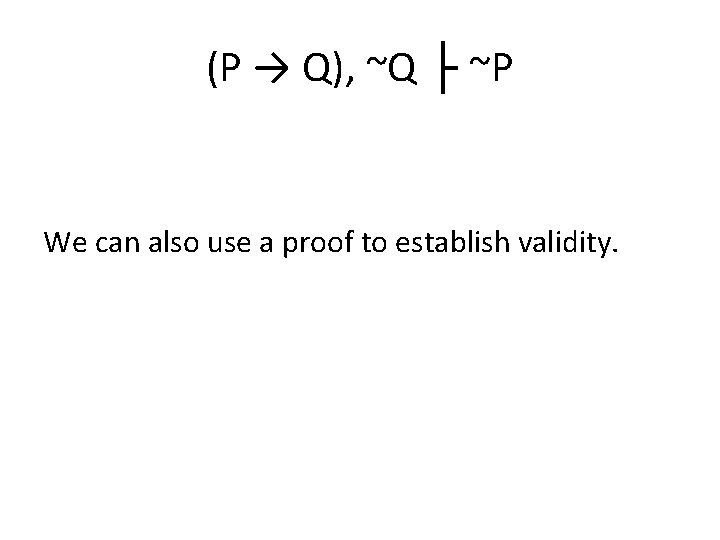






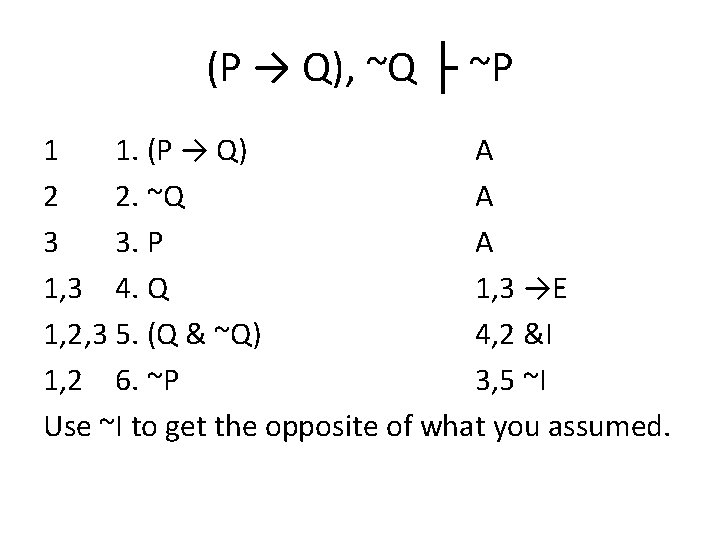


































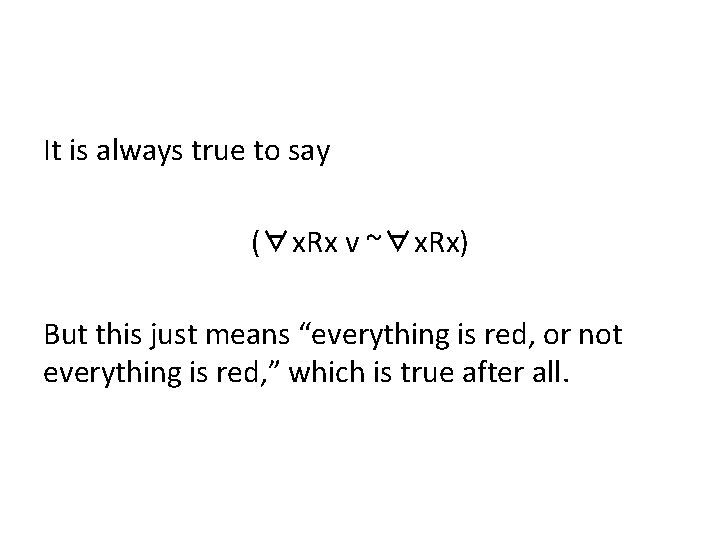

















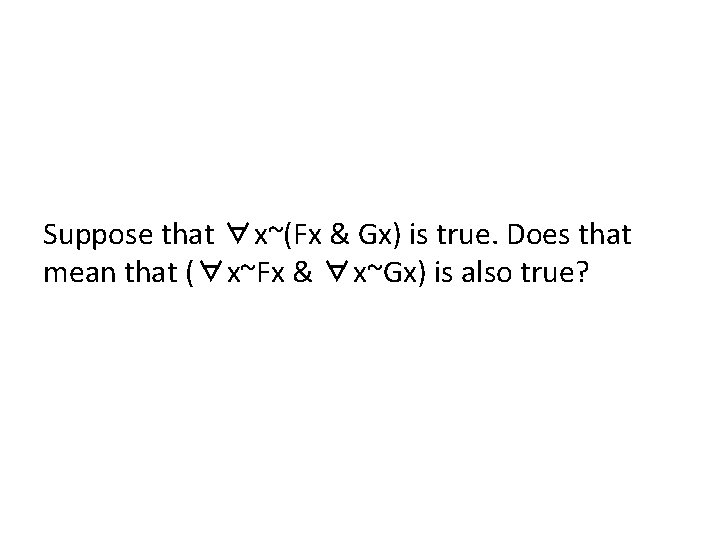



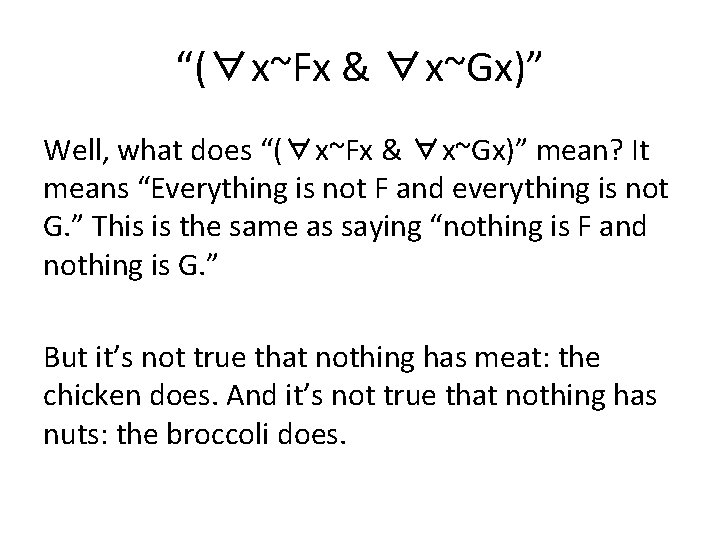




- Slides: 92

Predicate Logic

Goal of Logic The goal of logic is to develop formal tests for validity. This is done by finding deductively valid argument forms. In SL, we have two tests to determine valid argument forms: the truth-table test, and derivations. Any argument that has a form that is valid according to the truth-table test is valid, and any argument that has a form that can be proven is valid.

Example For example, here is a valid logical form: Premise: If P, then Q. Premise: Not-Q. Conclusion: Therefore, not-P.

Example We translate it into SL: Premise: (P → Q) Premise: ~Q Conclusion: ~P

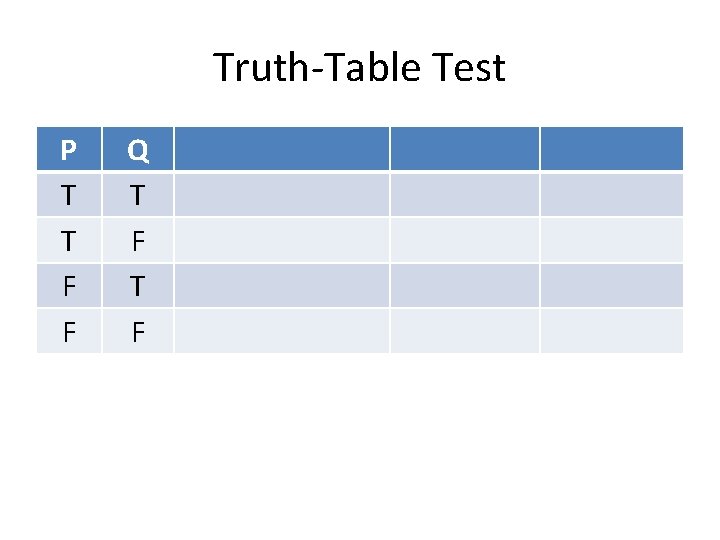
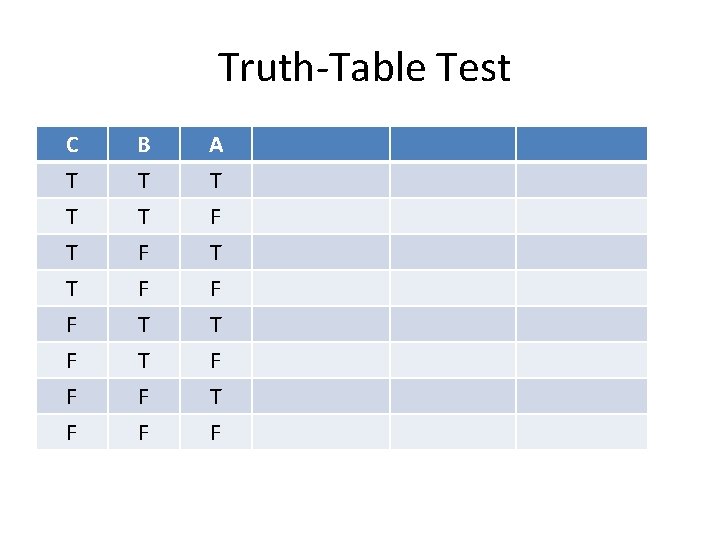
Truth-Table Test P T T F F Q T F

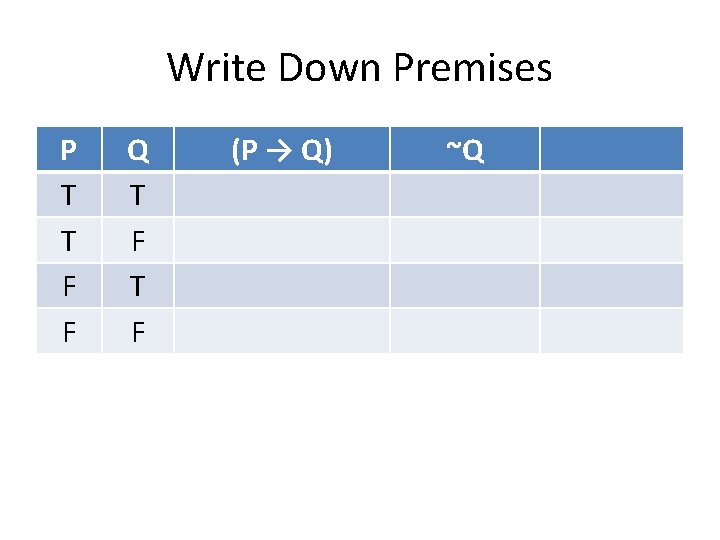
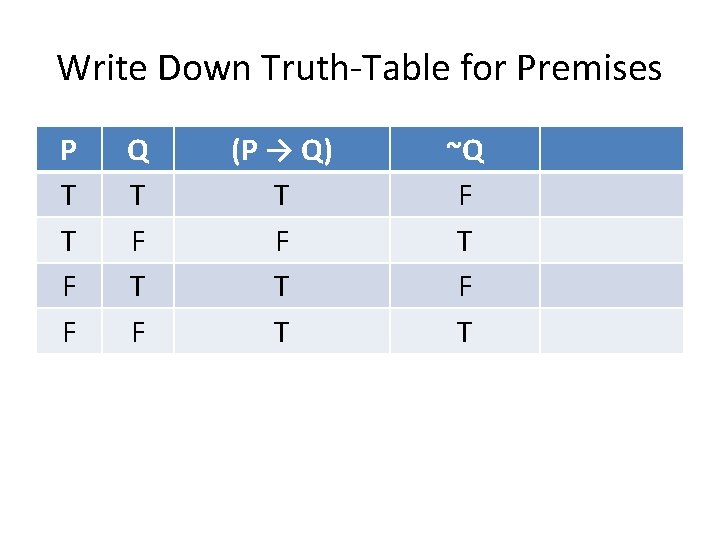
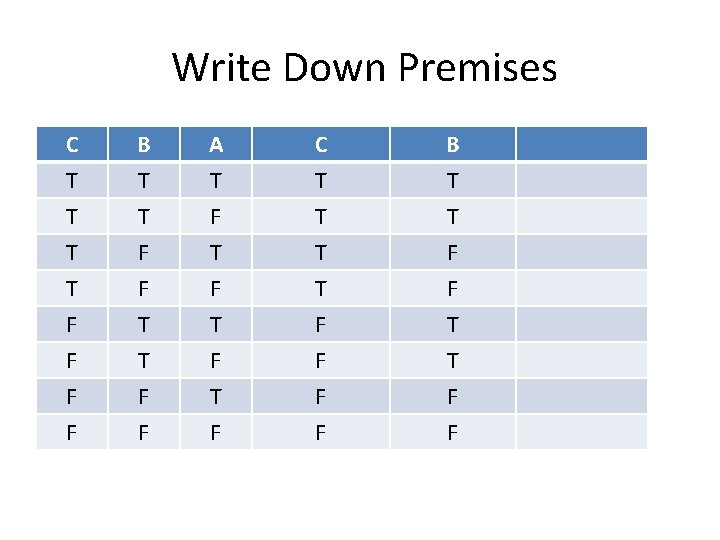
Write Down Premises P T T F F Q T F (P → Q) ~Q

Write Down Truth-Table for Premises P T T F F Q T F (P → Q) T F T T ~Q F T

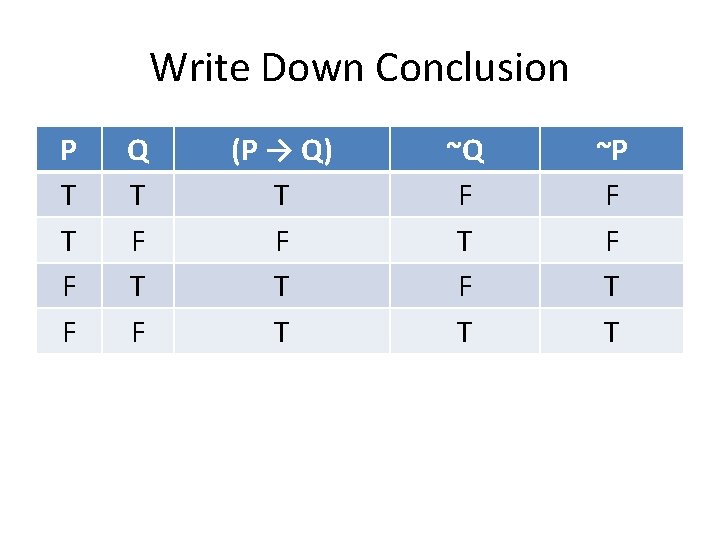
Write Down Conclusion P T T F F Q T F (P → Q) T F T T ~Q F T ~P F F T T

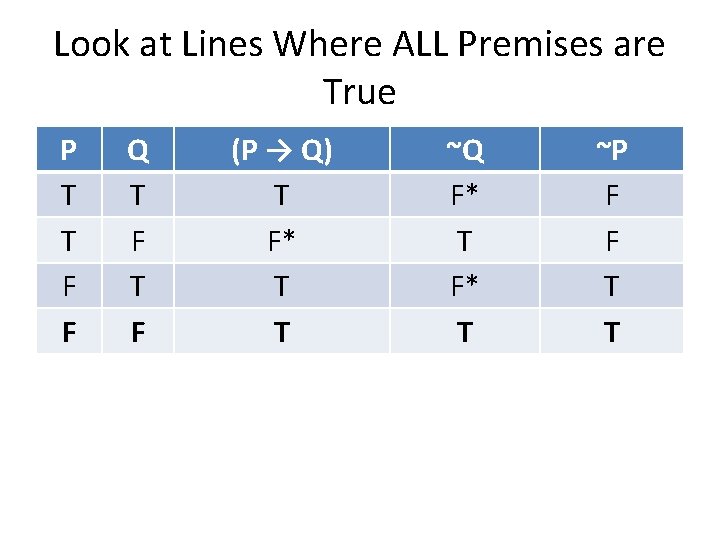
Look at Lines Where ALL Premises are True P T T F F Q T F (P → Q) T F* T T ~Q F* T ~P F F T T

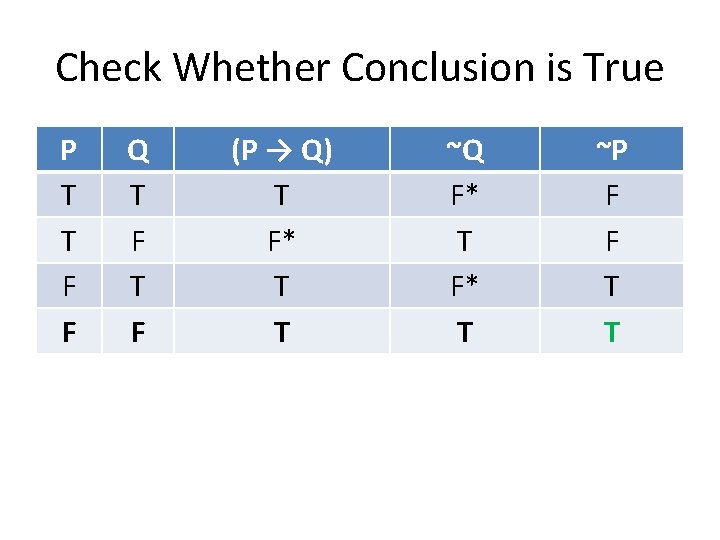
Check Whether Conclusion is True P T T F F Q T F (P → Q) T F* T T ~Q F* T ~P F F T T

(P → Q), ~Q ├ ~P This is how the truth-table test establishes the validity of the argument.
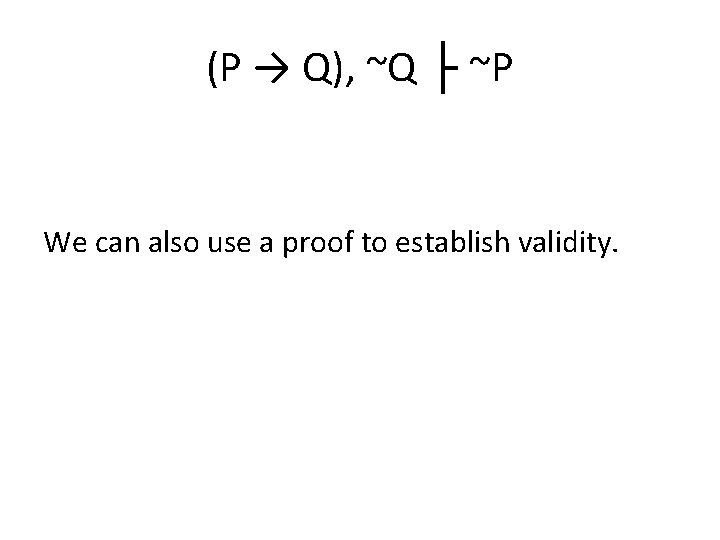
(P → Q), ~Q ├ ~P We can also use a proof to establish validity.

(P → Q), ~Q ├ ~P 1 1. (P → Q) A First, we write down the premises.

(P → Q), ~Q ├ ~P 1 1. (P → Q) A 2 2. ~Q A First, we write down the premises.

(P → Q), ~Q ├ ~P 1 1. (P → Q) A 2 2. ~Q A Then we look at what we want to prove.

~I To prove a negation, we often have to use the following strategy: 1. Assume the opposite of what we’re trying to prove. 2. Derive a contradiction. 3. Use ~I to get what we want.

(P → Q), ~Q ├ ~P 1 2 3 1. (P → Q) 2. ~Q 3. P Assume the opposite. A A A

(P → Q), ~Q ├ ~P 1 1. (P → Q) 2 2. ~Q 3 3. P 1, 3 4. Q 1, 2, 3 5. (Q & ~Q) Derive a contradiction. A A A 1, 3 →E 4, 2 &I
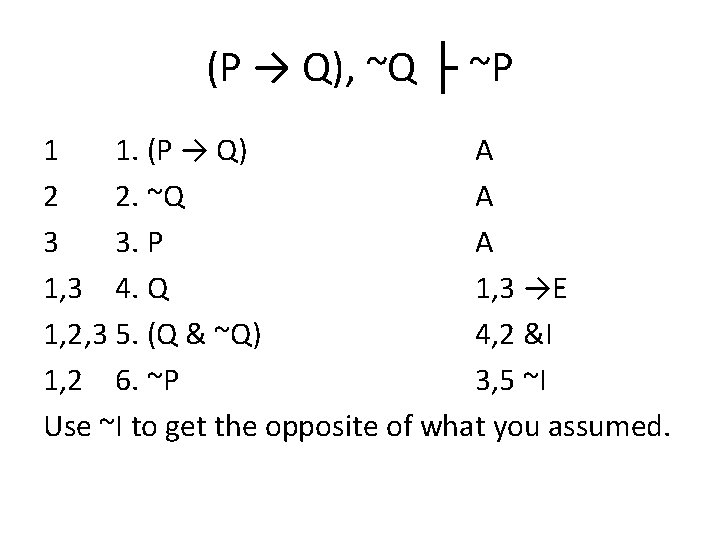
(P → Q), ~Q ├ ~P 1 1. (P → Q) A 2 2. ~Q A 3 3. P A 1, 3 4. Q 1, 3 →E 1, 2, 3 5. (Q & ~Q) 4, 2 &I 1, 2 6. ~P 3, 5 ~I Use ~I to get the opposite of what you assumed.

Valid Arguments that Don’t Pass But, there are still valid arguments that don’t pass the truth-table test for validity and aren’t provable in SL. (This is why failing the truth-table test does not show that an argument is invalid). For example: Premise: Michael is human. Conclusion: Therefore, someone is human.

Other Examples Premise: Every chicken is a bird. Premise: Every bird is an animal. Conclusion: Every chicken is an animal. Premise: No one comes to class on Saturday. Conclusion: Michael doesn’t come to class on Saturday.

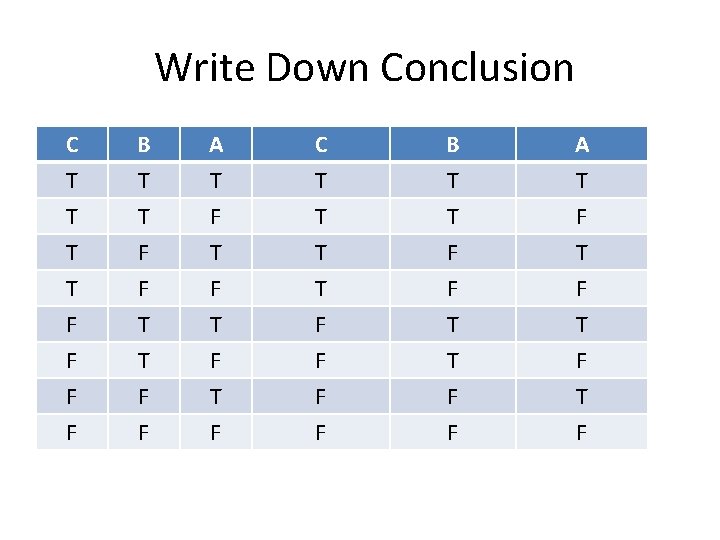
Other Examples Premise: Every chicken is a bird = C Premise: Every bird is an animal = B Conclusion: Every chicken is an animal = A Premise: No one comes to class on Saturday. Conclusion: Michael doesn’t come to class on Saturday.

Other Examples Premise: C Premise: B Conclusion: A Premise: No one comes to class on Saturday. Conclusion: Michael doesn’t come to class on Saturday.

Truth-Table Test C T T T B T T F A T F T T F F F T F

Write Down Premises C T T T B T T F A T F T C T T T B T T F F F T F T F F F T T F F

Write Down Conclusion C T T T B T T F A T F T T F F F F F T T F F F T F T F

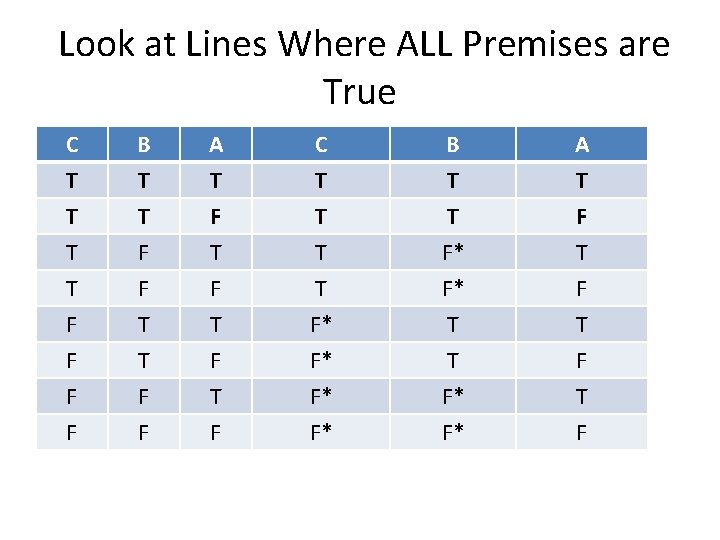
Look at Lines Where ALL Premises are True C T T T B T T F A T F T C T T T B T T F* A T F T T F F F T F T F* F* F* T T F* F* F T F

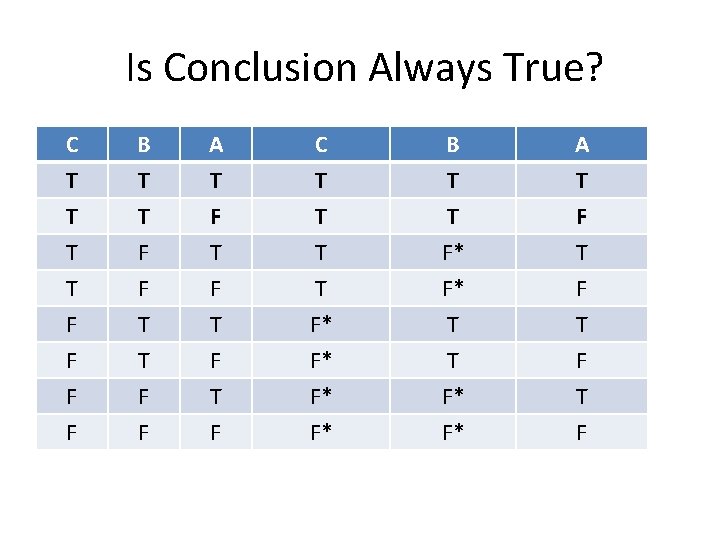
Is Conclusion Always True? C T T T B T T F A T F T C T T T B T T F* A T F T T F F F T F T F* F* F* T T F* F* F T F

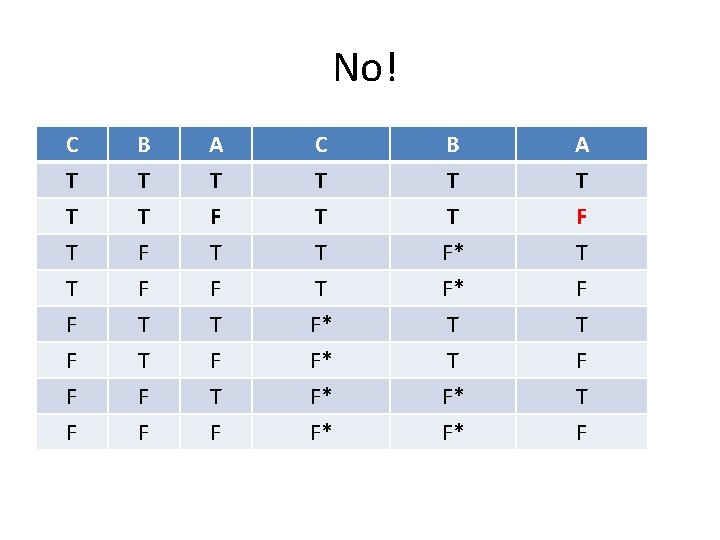
No! C T T T B T T F A T F T C T T T B T T F* A T F T T F F F T F T F* F* F* T T F* F* F T F

SL Not Expressive Enough The problem here is that our logic is not expressive enough. All simple English sentences get translated as sentence letters in SL. Therefore, no argument involving only simple sentences has a valid SL form, even though many such arguments are valid.

PL Therefore, we have a more expressive logic, predicate logic PL, which represents the parts of simple sentences. In PL, a sentence like “Michael is human” will have its parts “Michael” and “is human” translated separately. In particular, PL has a specific grammatical category for singular terms.

Singular Terms A singular term is an expression that names or identifies a particular individual, like a person or a city. English singular terms include:

Singular Terms • Proper names: ‘Michael, ’ ‘Jenny, ’ ‘Hong Kong, ’ etc. • ‘the’ + description: ‘the tallest man in the world, ’ ‘the country with the second largest economy, ’ ‘the third Wednesday of March, ’ etc. • ‘that’ ‘this’ or ‘that’ + description, ‘this’ + description: ‘this pencil, ’ ‘that table, ’ etc.

NOT Singular Terms • • ‘Every happy person’ ‘No one in Hong Kong’ ‘A bird with red feathers’ ‘Beautiful dresses’ None of these expressions name a particular individual or thing.

Translating Singular Terms To translate singular terms into PL, we will use lowercase Roman letters: a, b, c, d, e, f, g, etc. So we might translate “Michael” as “m. ” If we’re just doing logic (and not translating) usually we choose a, b, and c to be our singular terms.

Variables In addition, PL contains a special grammatical category called variables. Variables are a lot like singular terms, but they do not name or represent anything in particular. Variables: x, y, z (and if need be w, v, and u) We do not use these letters to translate singular terms!

Variables Replace Singular Terms Consider how variables are used in arithmetic: • 5 + 7 = 12 • 5 + x = 12 • y+x=z “ 5, ” “ 7, ” and “ 12” all name particular numbers. “x, ” “y, ” and “z” do not. But they go in the same places singular terms go.

Variables Replace Singular Terms In logic, things are very similar, except variables can replace more than just singular terms for numbers: • Michael gave that book to Sam • Michael gave x to Sam • y gave x to z

Open Sentences If you take an English sentence, remove one or more singular terms and replace them with variables, the result is an open sentence. • Michael gave x to Sam • x gave y to z • This past winter, x went home to visit x’s grandmother. • John went to the party but z stayed home.

Predicates Predicate logic also contains expressions that translate predicates. In traditional grammar, a sentence like “Michael is human” has “Michael” as its subject and “is human” as its predicate. In logic, we simply identify predicates as open sentences. So “x is human” is a predicate, but “is human” is not.

Translating Predicates in PL are translated as capital Roman letters: A, B, C, D, E, F, G, etc. We have a preference for the letters F, G, and H when there is no other reason to choose.

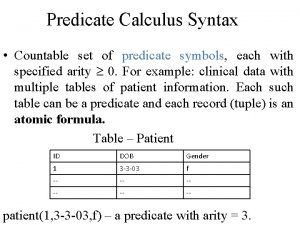
Our Fragment Predicate logic is a lot harder than sentential logic, so to make it easier, the system in the reading (PL) only has “monadic” or “one-place” predicates– predicates containing only one place for a singular term.

Only 1 -Place Predicates OK: • x is human • Michael gave z to Sam • y gave that book to Sam • Michael gave that book to y NOT OK: • x gave that book to y • x admires z

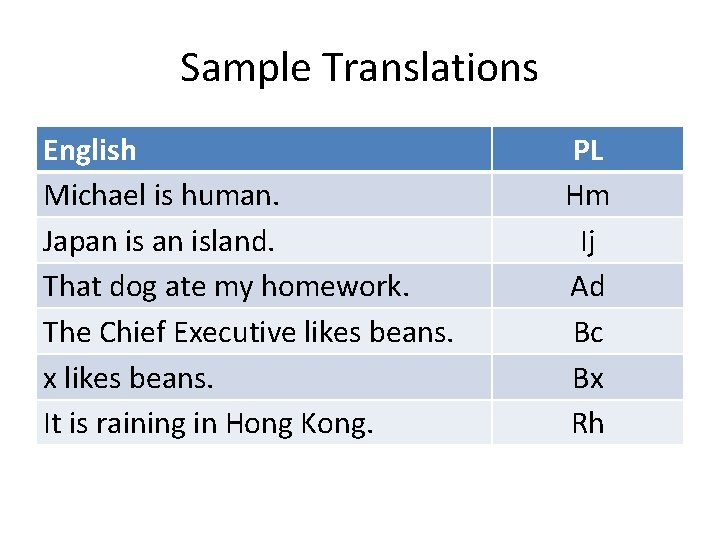
Sample Translations English Michael is human. Japan island. That dog ate my homework. The Chief Executive likes beans. x likes beans. It is raining in Hong Kong. PL Hm Ij Ad Bc Bx Rh

More Complicated WFFs Just as in SL, we can combine PL WFFs with truth -functional connectives: • (Hm & Bc) • ((Rh ↔ Ij) v (Ad → ~Bc))

Quantifiers Some words in English are not appropriately translated as either singular terms or predicates. Consider the sentence: “Something is red. ” Here we know that “x is red” translates as “Rx. ” How should we represent “something”?

Not a Singular Term It would be a bad idea to translate “something” as a singular term: First, “something” doesn’t identify a particular individual.

Not a Singular Term It would be a bad idea to translate “something” as a singular term: Second, if we translated “Something” as a singular term “s” and “something is red” as “Rs, ” then we would have to translate “something is red and something is not red” as “(Rs & ~Rs). ”

Not a Contradiction But it’s not a contradiction if something is red and something (else) is not red. This is why singular terms have to identify particular individuals, and why we can’t translate words like “something” as singular terms.

Quantifiers In PL, there is a special symbol that translates “something”: ∃ (called “backwards E” or “the existential quantifier”). In the grammar of PL, to write “something is red” we write ∃ followed by a variable, followed by an open sentence with that variable in it: ∃x. Rx

∃x. Rx We can say this like: “there is some thing x, and x is red. ” “for at least one object x, x is red. ” “something is red. ”

∃x. Rx Continuing to translate “Rx” as x is red: ∃x. Rx is true when there is some object o where Ro is true. For example, if “p” translates “this red pen” then ∃x. Rx is true because Rp is true.

Not a Contradiction This is how it’s possible that “something is red and something is not red”: (∃x. Rx & ∃x~Rx) The first conjunct is true if there’s some object that is red (this red pen) and the second is true if there’s some object that’s not red (my shirt).

Note Which variable we use after ∃ doesn’t matter, these statements are all equivalent: ∃x. Rx ∃y. Ry ∃z. Rz

Note However, we must use the same variable in the open formula that we wish to bind: YES: ∃z. Rz NO: ∃y. Rz

“Everything” Let’s look now at the sentence “Everything is red. ” “Everything” does not identify a particular individual, and it would be wrong to translate “everything” as a singular term like “e. ”

Bad Translation (P v ~P) is a logical truth (its truth-table has only T’s in it). So (Re v ~Re) is also a logical truth. If we translated “x is red” as “Rx” and “everything” as “e” we would have: (Re v ~Re) Everything is red or everything is not red. But that’s not true, it’s false!

Universal Quantifier: ∀ In PL we have a special symbol for “everything”: ∀ (called “upside-down A”– it’s supposed to suggest All). So if I want to say “everything is red” in PL, I write: ∀x. Rx Or: ∀y. Ry ∀z. Rz

∀x. Rx The way to read this is: “For all things x, x is red. ” “Every x is such that x is red. ” “Everything is red. ”

Now if we wanted to translate “Everything is red or everything is not red, ” we would write: (∀x. Rx v ∀x~Rx) This is not a logical truth.
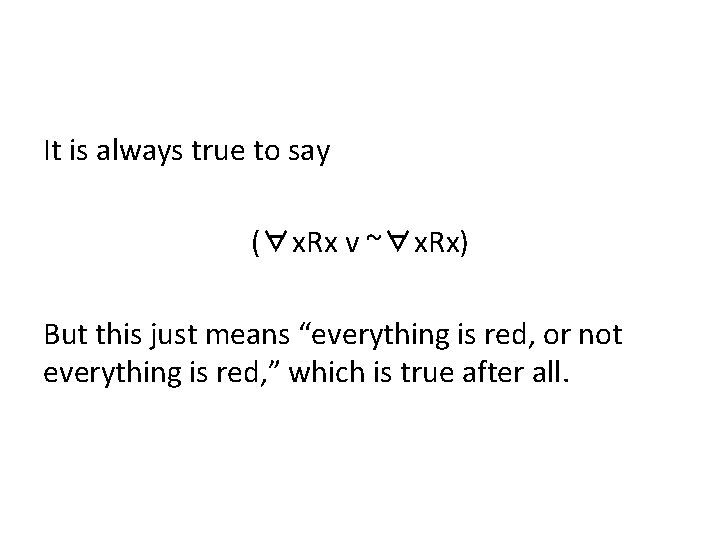
It is always true to say (∀x. Rx v ~∀x. Rx) But this just means “everything is red, or not everything is red, ” which is true after all.

Restricted Quantifiers Often we don’t talk about something or everything, but instead talk about some person or every person, or some dog or every dog, or some student or every student. We can use the quantifiers ∀ and ∃ here too.

“Some Student is Happy” Let: Sx : = x is a student Hx : = x is happy Then ∃x(Sx & Hx) Means that some student is happy; at least one student is happy; there is some thing x where x is a student and x is happy.

“Every Student is Happy” What about “every student is happy. ” Can we write: ∀x(Sx & Hx) No. This says “For every thing x that exists, x is a student and x is happy. ” But even if every student is happy, it’s not true that everything is a student, and it’s not true that everything is happy!

“Every Student is Happy” Instead, we write: ∀x(Sx → Hx) This may seem strange, but think about what it means. It says “for every thing x that exists, IF that thing is a student, THEN that thing is happy. ”

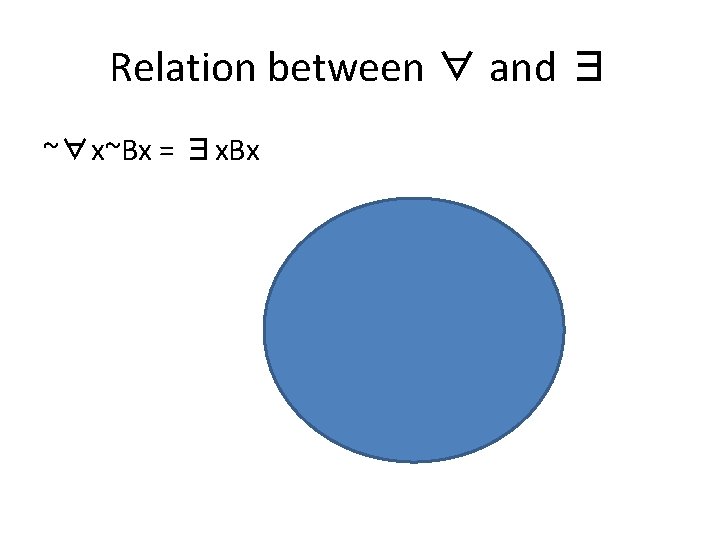
Relation between ∀ and ∃ The quantifiers are related in the following way: ∀x. Fx = ~∃x~Fx ∀x~Fx = ~∃x. Fx ~∀x. Fx = ∃x~Fx ~∀x~Fx = ∃x. Fx

Relation between ∀ and ∃ Why is this true? Let’s think about ~∀x~Fx = ∃x. Fx The first part “~∀x~Fx” says “not everything is not F. ” The second part “∃x. Fx” says “something is F. ” If not everything is not F, then something must be F.

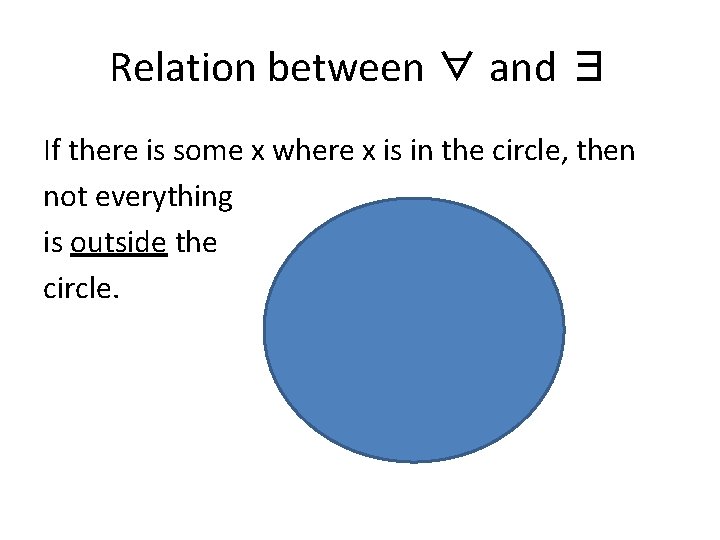
Relation between ∀ and ∃ Let’s suppose we put all the blue things in the circle:

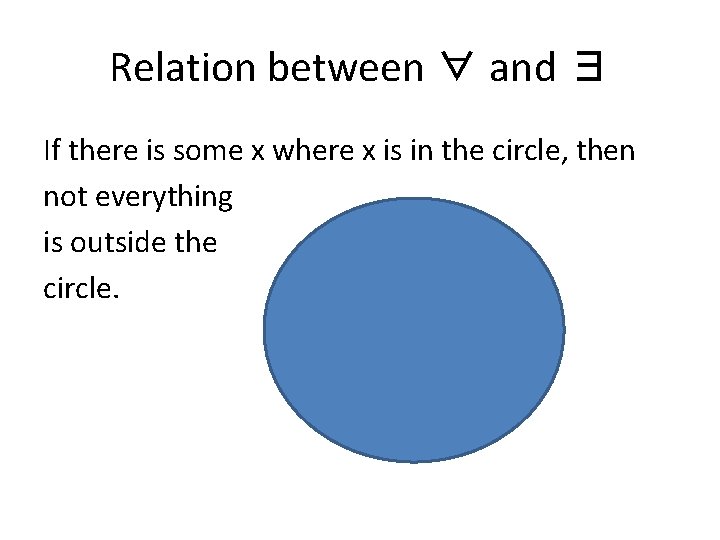
Relation between ∀ and ∃ If there is some x where x is in the circle, then not everything is outside the circle.

Relation between ∀ and ∃ If there is some x where x is in the circle, then not everything is outside the circle.

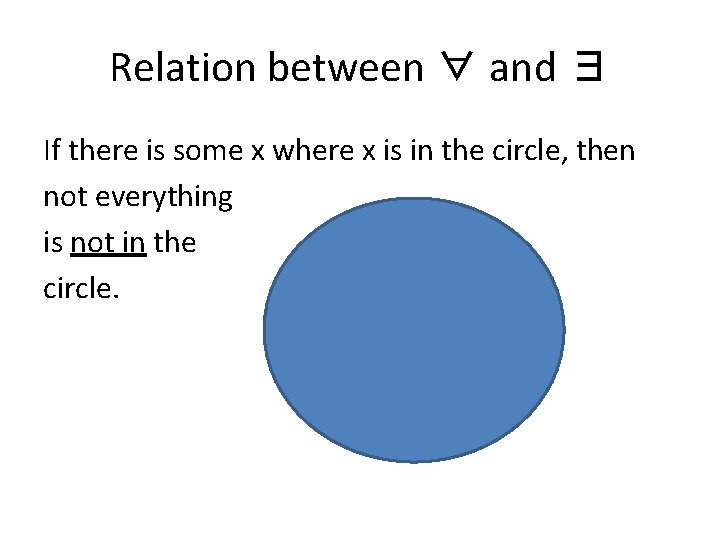
Relation between ∀ and ∃ If there is some x where x is in the circle, then not everything is not in the circle.

Relation between ∀ and ∃ ~∀x~Bx = ∃x. Bx

Relation between ∀ and ∃ Let’s think about ∀x~Fx = ~∃x. Fx The first part “∀x~Fx” says “everything is not F. ” The second part “~∃x. Fx” says “it’s not true that something is F. ” If everything is not F, then nothing is F, so it’s not true that something is F.

Relation between ∀ and ∃ Imagine that all of the green things are in this circle.

Relation between ∀ and ∃ Now suppose that everything is not in the circle.

Relation between ∀ and ∃ So there aren’t any green things.

Relation between ∀ and ∃ So there is not something that is inside the circle.

Relation between ∀ and ∃ So there is not something that is inside the circle.

Relation between ∀ and ∃ ∀x~Fx = ~∃x. Fx

“Nothing” This also suggests how we should translate sentences involving “nothing” or “no”: Nothing is red: ~∃x. Rx Nothing is red: ∀x~Rx No dog is red: ~∃x(Dx & Rx) No dog is red: ∀x(Dx → ~Rx)


Entailment Here’s a problem that’s VERY SIMILAR to one that will appear on the final. Which of these two formulas entails the other? Explain your answer. ∀x~(Fx & Gx) (∀x~Fx & ∀x~Gx)

Entailment φ entails ψ when there is a valid argument from φ as its only premise to ψ as its conclusion. That is, if φ is true then ψ is true. Suppose that (∀x~Fx & ∀x~Gx) is true. Does that mean that ∀x~(Fx & Gx) is also true?
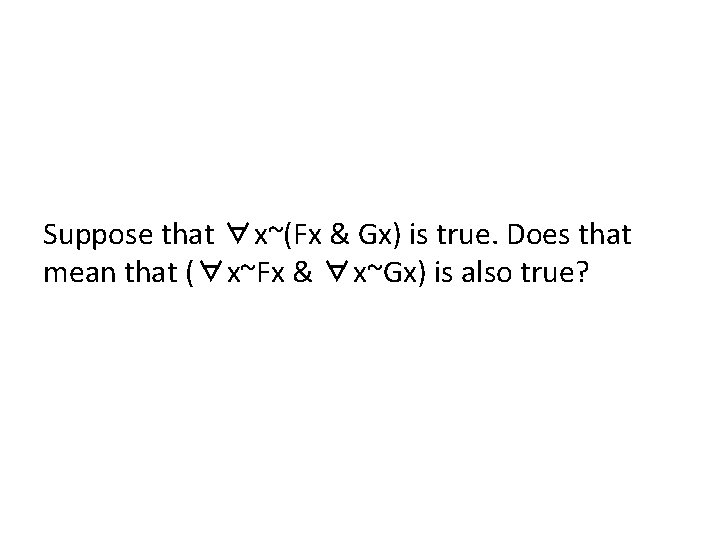
Suppose that ∀x~(Fx & Gx) is true. Does that mean that (∀x~Fx & ∀x~Gx) is also true?

Example Let’s imagine a concrete example. You go to a private kitchen with your friends. You know that half of them are vegetarians and cannot eat meat, and half of them are allergic to nuts and cannot eat nuts. You ask the restaurant to make a menu where nothing has both meat and nuts in it: ∀x~(Fx & Gx): for every x that you eat, it is not true that x has meat AND x has nuts.

Example Here’s the menu they come up with: Menu Broccoli & cashews (nuts) w/ no meat Chicken (meat) & rice w/ no nuts Ice cream w/ no meat, no nuts

The restaurant has accepted your premise. Nothing has both meat and nuts in it: ∀x~(Fx & Gx). But is it true that (∀x~Fx & ∀x~Gx) ?
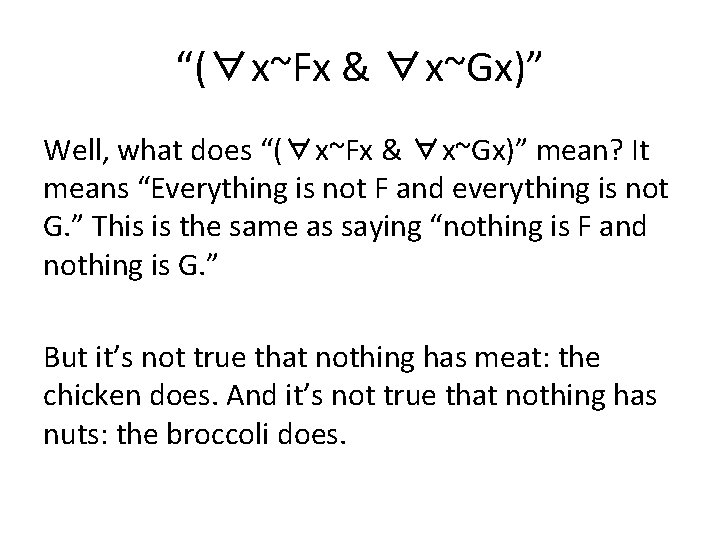
“(∀x~Fx & ∀x~Gx)” Well, what does “(∀x~Fx & ∀x~Gx)” mean? It means “Everything is not F and everything is not G. ” This is the same as saying “nothing is F and nothing is G. ” But it’s not true that nothing has meat: the chicken does. And it’s not true that nothing has nuts: the broccoli does.

This inference is invalid: Premise: ∀x~(Fx & Gx) Conclusion: (∀x~Fx & ∀x~Gx) What about the other inference? Premise: (∀x~Fx & ∀x~Gx) Conclusion: ∀x~(Fx & Gx)

Example Let’s imagine a concrete example. You go to a private kitchen with your friends and you call ahead to make sure that nothing has meat in it = ∀x~Fx (because some of your friends are vegetarians) and that nothing has nuts in it = ∀x~Gx (because some of your friends are allergic). The restaurant says: “Yes, we can handle your request. ”

Menu To accommodate you, the restaurant makes a menu where no dishes have meat and no dishes have nuts: Menu: 1. Broccoli w/ no meat, no nuts 2. Tofu w/ no meat, no nuts 3. Ice cream w/ no meat, no nuts

∀x~(Fx & Gx) The restaurant has accepted your premise: it’s true that (∀x~Fx & ∀x~Gx): no dishes have meat (1, 2, and 3) and also no dishes have nuts (1, 2, and 3 again). But is it true that: ∀x~(Fx & Gx) ? This says nothing has both meat and nuts in it. And nothing does! So this inference is valid, and (∀x~Fx & ∀x~Gx) entails ∀x~(Fx & Gx).
 Predicate adjective diagramming
Predicate adjective diagramming Predicate nominative examples
Predicate nominative examples Predicate nouns and predicate adjectives
Predicate nouns and predicate adjectives Predicate nominatives and predicate adjectives
Predicate nominatives and predicate adjectives Predicate nominative
Predicate nominative Complete predicate and simple predicate examples
Complete predicate and simple predicate examples Diagramming subject complements
Diagramming subject complements Predicate logic
Predicate logic Predicate logic rules of inference
Predicate logic rules of inference Predicate logic equivalence
Predicate logic equivalence Current king of france
Current king of france The first order chapter 8
The first order chapter 8 Semantics of predicate logic
Semantics of predicate logic What is predicate logic example
What is predicate logic example Predicate logic tutorial
Predicate logic tutorial The main goal of logic is to
The main goal of logic is to Concurrent vs sequential
Concurrent vs sequential Combinational logic sequential logic 차이
Combinational logic sequential logic 차이 First order logic vs propositional logic
First order logic vs propositional logic Tw
Tw Logic chapter 3
Logic chapter 3 First order logic vs propositional logic
First order logic vs propositional logic Combinational logic sequential logic 차이
Combinational logic sequential logic 차이 First order logic vs propositional logic
First order logic vs propositional logic Is it x y or y x
Is it x y or y x điện thế nghỉ
điện thế nghỉ Biện pháp chống mỏi cơ
Biện pháp chống mỏi cơ Một số thể thơ truyền thống
Một số thể thơ truyền thống Trời xanh đây là của chúng ta thể thơ
Trời xanh đây là của chúng ta thể thơ Slidetodoc
Slidetodoc Thiếu nhi thế giới liên hoan
Thiếu nhi thế giới liên hoan Số nguyên tố là gì
Số nguyên tố là gì Phối cảnh
Phối cảnh Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất Sơ đồ cơ thể người
Sơ đồ cơ thể người Tư thế ngồi viết
Tư thế ngồi viết Bàn tay mà dây bẩn
Bàn tay mà dây bẩn đặc điểm cơ thể của người tối cổ
đặc điểm cơ thể của người tối cổ Cách giải mật thư tọa độ
Cách giải mật thư tọa độ Tư thế worms-breton
Tư thế worms-breton Bổ thể
Bổ thể Tư thế ngồi viết
Tư thế ngồi viết ưu thế lai là gì
ưu thế lai là gì Thẻ vin
Thẻ vin Thơ thất ngôn tứ tuyệt đường luật
Thơ thất ngôn tứ tuyệt đường luật Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Từ ngữ thể hiện lòng nhân hậu
Từ ngữ thể hiện lòng nhân hậu Diễn thế sinh thái là
Diễn thế sinh thái là Giọng cùng tên là
Giọng cùng tên là Phép trừ bù
Phép trừ bù Chúa sống lại
Chúa sống lại Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Lời thề hippocrates
Lời thề hippocrates Hổ đẻ mỗi lứa mấy con
Hổ đẻ mỗi lứa mấy con đại từ thay thế
đại từ thay thế Vẽ hình chiếu vuông góc của vật thể sau
Vẽ hình chiếu vuông góc của vật thể sau Quá trình desamine hóa có thể tạo ra
Quá trình desamine hóa có thể tạo ra Công của trọng lực
Công của trọng lực Thế nào là mạng điện lắp đặt kiểu nổi
Thế nào là mạng điện lắp đặt kiểu nổi Hát kết hợp bộ gõ cơ thể
Hát kết hợp bộ gõ cơ thể Dạng đột biến một nhiễm là
Dạng đột biến một nhiễm là Vẽ hình chiếu đứng bằng cạnh của vật thể
Vẽ hình chiếu đứng bằng cạnh của vật thể độ dài liên kết
độ dài liên kết Các môn thể thao bắt đầu bằng tiếng chạy
Các môn thể thao bắt đầu bằng tiếng chạy Voi kéo gỗ như thế nào
Voi kéo gỗ như thế nào Khi nào hổ con có thể sống độc lập
Khi nào hổ con có thể sống độc lập Predicate nominative examples
Predicate nominative examples Whats a complete predicate
Whats a complete predicate Predicate nominative
Predicate nominative Subject and predicate
Subject and predicate Simple sentence with a compound predicate
Simple sentence with a compound predicate Tell me the subject
Tell me the subject Simple subject and simple predicate
Simple subject and simple predicate Predicate device
Predicate device Simple subject and simple predicate
Simple subject and simple predicate Infinitive adverb
Infinitive adverb Predicate complement
Predicate complement Predicate offence for money laundering
Predicate offence for money laundering Predicate noun
Predicate noun Predicate noun
Predicate noun Plp 11
Plp 11 Is she a subject
Is she a subject Exclamatory sentences
Exclamatory sentences Slow and steady wins the race find the predicate
Slow and steady wins the race find the predicate What is a simple predicate
What is a simple predicate 20 sentences with subject and predicate
20 sentences with subject and predicate Obedience to teachers
Obedience to teachers Predicate nominative
Predicate nominative Latin predicate nominative
Latin predicate nominative Simple predicate
Simple predicate Simple predicate examples
Simple predicate examples Whats a complete predicate
Whats a complete predicate