Ideal Gas Laws The Ideal Gas Laws The



































- Slides: 48

Ideal Gas Laws

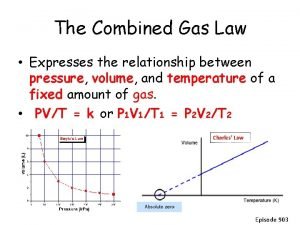
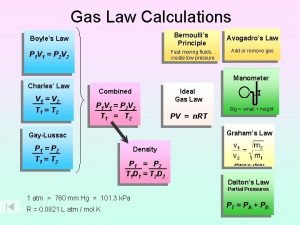
The Ideal Gas Laws • The gas laws relate pressure, volume, and temperature of an ideal gas. Boyle’s Law: P 1 V 1 = P 2 V 2 Charles’ Law: Ideal Gas Law: PV = n. RT ***The number of molecules of the gas must remain constant.

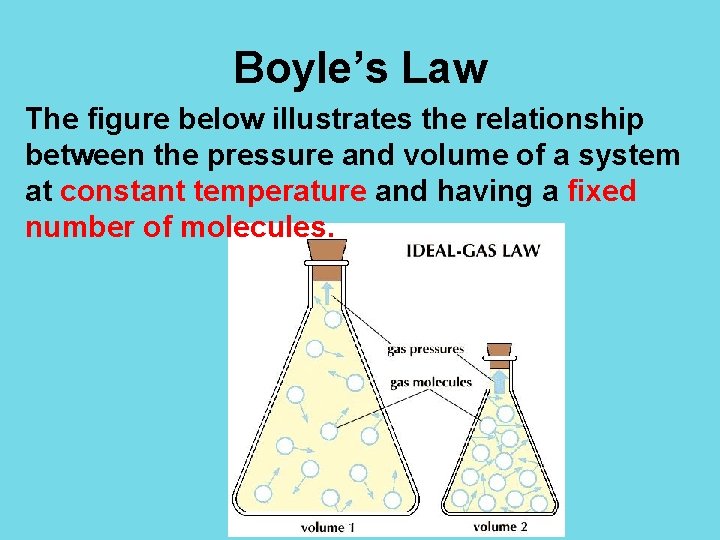
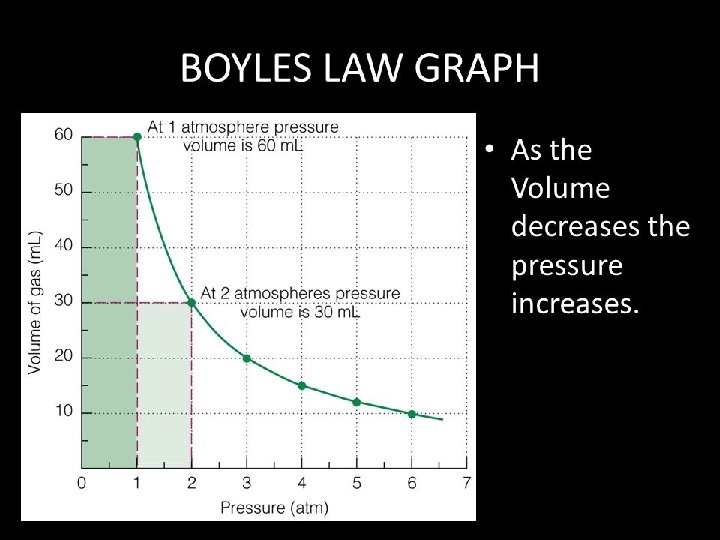
Boyle’s Law The figure below illustrates the relationship between the pressure and volume of a system at constant temperature and having a fixed number of molecules.

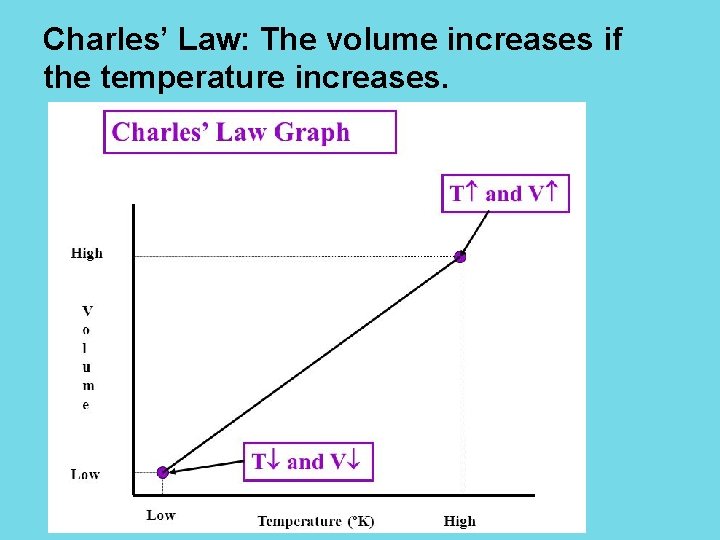
Charles’ Law The figure below shows how the volume changes if the temperature is increased for a system at constant pressure and having a constant number of molecules.

Boyle’s Law • Must be a fixed amount of gas (constant number of molecules) • Must be at constant temperature • Changing the volume causes an opposite change in the pressure Increasing the volume causes a decrease in the pressure OR Increasing the pressure causes a decrease in the volume

Boyle’s Law A diver blows a 0. 75 L air bubble 10 m under water. As it rises to the surface, the pressure goes from 2. 25 atm to 1. 03 atm. What will be the volume of air in the bubble at the surface? P 1 = 2. 25 atm P 2 = 1. 03 atm V 1 = 0. 75 L V 2 = ? (2. 25 atm)(0. 75 L) = (1. 03 atm)(V 2) V 2 =

Learning Check Give the values of P 1, V 1, P 2, and V 2 for the following: A bag of potato chips is packaged at sea level (1. 00 atm) and has a volume of 315 m. L. If this bag of chips is transported to Denver (0. 775 atm), what will the new volume of the bag be? P 1 = P 2 = V 1 = V 2 =

Charles’ Law • Must be a fixed amount of gas (constant number of molecules) • Must be at constant pressure • Temperature must be in Kelvin ***** • Changing the volume causes the temperature to change in the same direction Increasing the volume causes the temperature to increase OR Increasing the temperature causes the

Charles’ Law Can you think of evidence of Charles’ Law? What would happen if we put an inflated balloon in the freezer?

Converting Temperature to Kelvin To convert temperature from degrees C to Kelvin, simply add 273 to the temperature in degrees C. 25. 0 o. C = 273 + 25 = 298 K Convert 60. 0 o. C to temperature in K: 60. 0 o. C = ? 60. 0 o. C = 273 + 60 = 333 K

Charles’ Law A helium balloon in a closed car occupies a volume of 2. 32 L at 40. 0 o. C. If the car is parked on a hot day and the temperature inside rises to 75. 0 o. C, what is the new volume of the balloon, assuming the pressure remains constant? V 1 = 2. 32 L T 1 = 40. 0 o. C V 2 = ? T 2 = 75. 0 o. C T 1 = T 2 =

Charles’ Law Remember, Charles’ Law states:

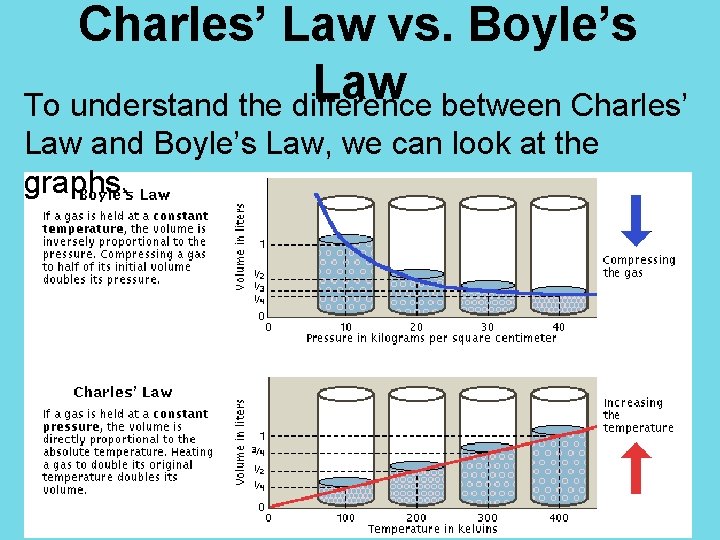
Charles’ Law vs. Boyle’s Law To understand the difference between Charles’ Law and Boyle’s Law, we can look at the graphs.

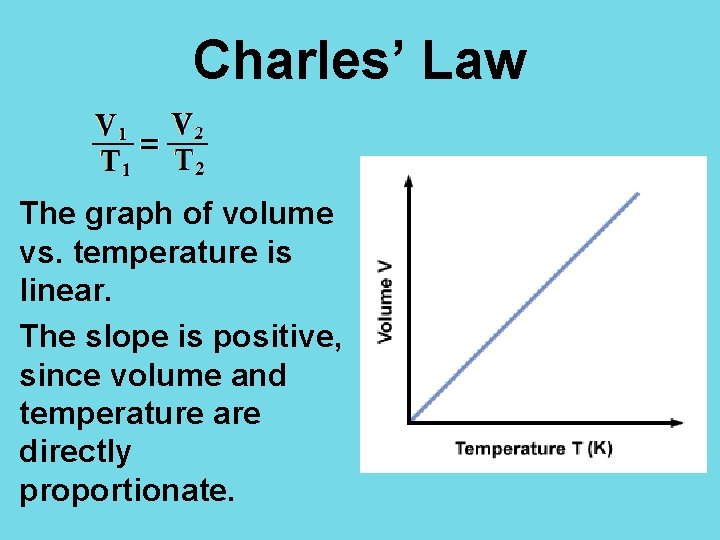
Charles’ Law The graph of volume vs. temperature is linear. The slope is positive, since volume and temperature are directly proportionate.

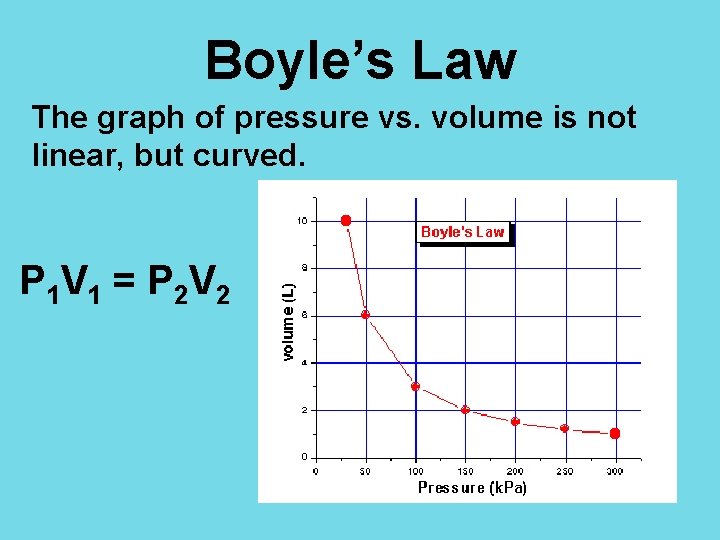
Boyle’s Law The graph of pressure vs. volume is not linear, but curved. P 1 V 1 = P 2 V 2

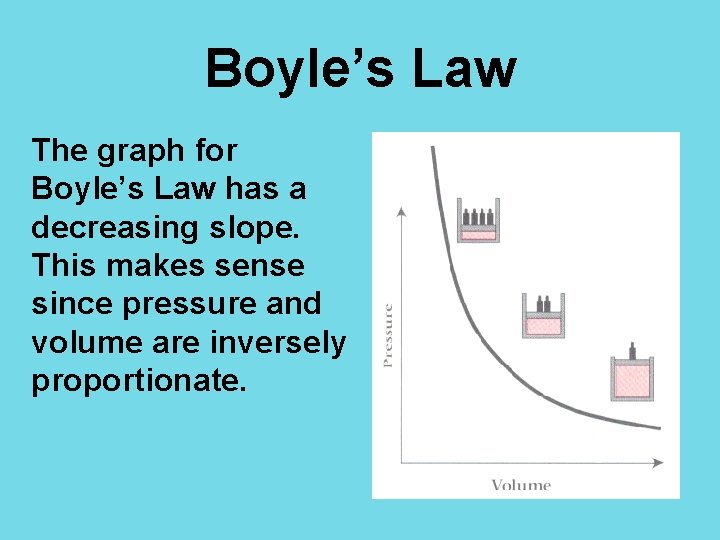
Boyle’s Law The graph for Boyle’s Law has a decreasing slope. This makes sense since pressure and volume are inversely proportionate.

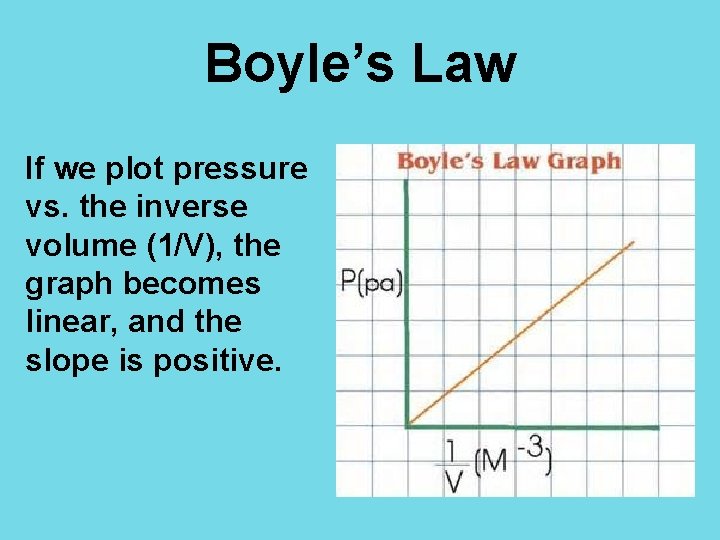
Boyle’s Law If we plot pressure vs. the inverse volume (1/V), the graph becomes linear, and the slope is positive.

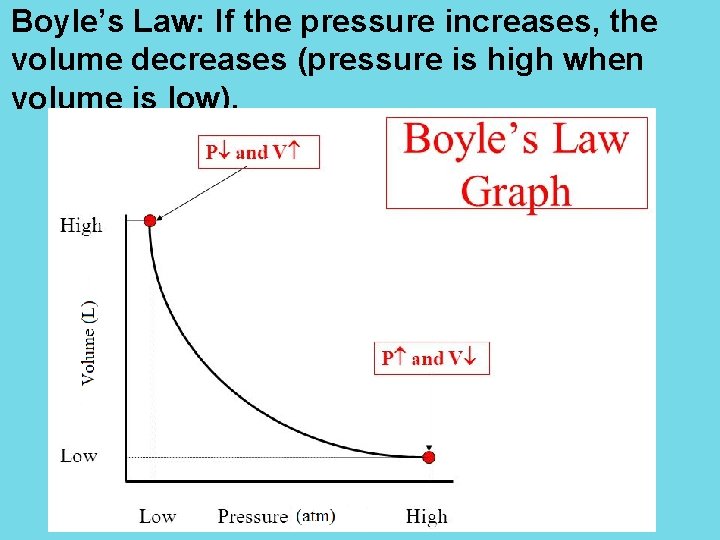
Boyle’s Law: If the pressure increases, the volume decreases (pressure is high when volume is low).

Charles’ Law: The volume increases if the temperature increases.


Combined Gas Law If temperature (T), pressure (P), and volume (V) are allowed to interact (change), we use the Combined Gas Law: P 1 V 1 P 2 V 2 = T 1 T 2 Only the number of molecules of gas remains constant for the Combined Gas Law.

Combined Gas Law • As always, the number of molecules of the gas must remain constant. • As in Charles’ Law, the temperature must be in Kelvin. • Gas Law problems will often refer to STP = standard temperature and pressure = 273 K and 1 atm • Record all units!!

Combined Gas Law A weather balloon contains 4. 0 L of hydrogen gas (H 2) at STP. What is the volume of H 2 gas at 2. 0 atm and 30 o. C? P 1 = V 1 = T 1 = P 2 = V 2 = T 2 =

Combined Gas Law A weather balloon contains 4. 0 L of hydrogen gas (H 2) at STP. What is the volume of H 2 gas at 2. 0 atm and 30 o. C? P 1 = 1. 0 atm V 1 = 4. 0 L T 1 = 273 K P 2 = 2. 0 atm V 2 = ? T 2 = 30 + 273 = 303 K

Combined Gas Law A weather balloon contains 4. 0 L of hydrogen gas (H 2) at STP. What is the volume of H 2 gas at 2. 0 atm and 30 o. C? P 1 V 1 P 2 V 2 T 1 = T 2 V 2 = (0. 0147 Latm/K)(151. 5 K/atm) V 2 = 2. 23 L

Learning Check Does our answer make sense? • Pressure was doubled Volume ? • Temperature increased Volume? What was the volume we calculated? How does it compare to the predictions above?

Learning Check Does our answer make sense? • Pressure was doubled Volume cut in half • Temperature increased Volume increase Our volume was a little bit more than half the original volume. Based on the predicted changes above, this makes sense.

Learning Check A sample of 2. 9 liters of gas at 5 atm and 50 o. C is compressed to 2. 4 liters and 3 atm. What is the new temperature of the gas? P 1 = V 1 = T 1 = P 2 = V 2 = T 2 =

Learning Check A 2135 cm 3 sample of dry air has a pressure of 98. 4 k. Pa at 127 o. C. What is the volume of the sample if the temperature is increased to 206 o. C when the pressure is kept constant? a) 1320 cm 3 b) 1780 cm 3 c) 2560 cm 3 d) 3460 cm 3

Learning Check T 1 = 127 + 273 = 400 K V 1 = 2135 cm 3 T 2 = 206 + 273 = 479 K V 2 = ? V 2 = 2557 cm 3

Ideal Gas Law PV =n. RT n = number of moles of gas R = ideal gas constant = 0. 0821 OR = 8. 314 As usual, the temperature must be in Kelvin.

Learning Check Calculate the number of moles of NH 3 in a 3. 0 L container at 300 K and a pressure of 1. 50 atm. P = 1. 50 atm V = 3. 0 L T = 300 K R = 0. 0821

Learning Check Calculate the number of moles of NH 3 in a 3. 0 L container at 300 K and a pressure of 1. 50 atm. PV = n. RT (1. 50 atm)(3. 0 L) = n(0. 0821 n = 0. 183 mol NH 3 )(300 K)

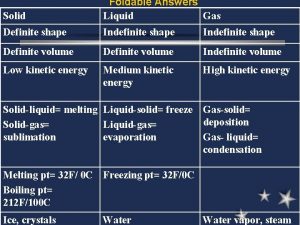
What is an Ideal Gas? Ideal gases: • Follow kinetic-molecular theory • Gas particles take up no space • Gas particles have no intermolecular attractions • Gas particles have no attraction/repulsion with container walls • Particles have random motion but travel in straight lines until a collision occurs • Collisions do not change the kinetic energy of the system

Ideal vs. Real Gases No gas is 100% ideal, though many are good approximations. In reality, the particles of all gases take up some volume (space) and have some attractive forces. When is it not fair to assume the gas is an ideal gas?

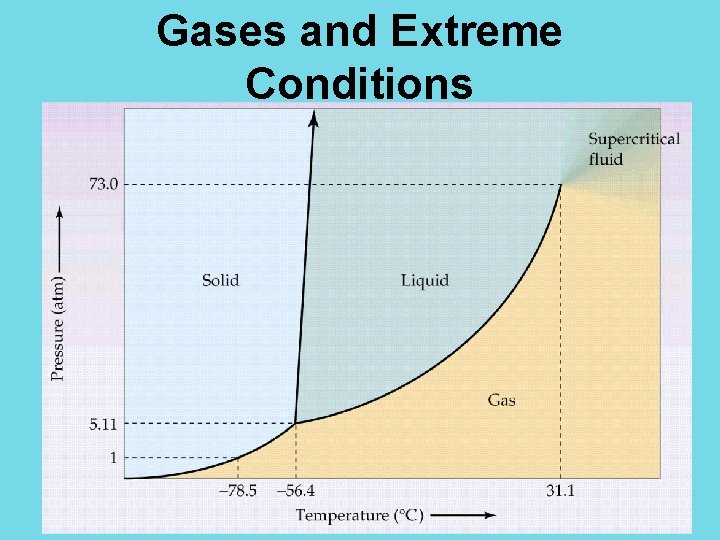
Ideal vs. Real Gases do not behave the same under all conditions. At extreme temperatures and pressures, gases do not behave as ideal gases. Very low temperatures: molecules move very slowly, and eventually the gas will become a liquid (phase change known as condensation) Very high pressures: molecules become very close together, and attractions between molecules become more important. Again, the gas will become a

Gases and Extreme Conditions

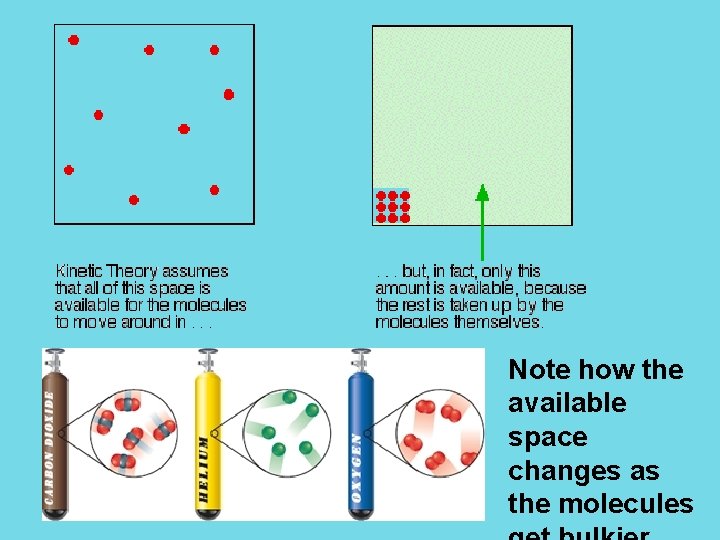
Ideal vs. Real Gases There are other conditions under which gases stop being ideal gases. Polar molecules: the partial charges on the “poles” of the molecule make the intermolecular attractions are important Large, bulky molecules: the larger size of these molecules cause them to differ from ideal gases because the larger size reduces the available volume of the container (these molecules take up a noticeable amount of space)

Note how the available space changes as the molecules

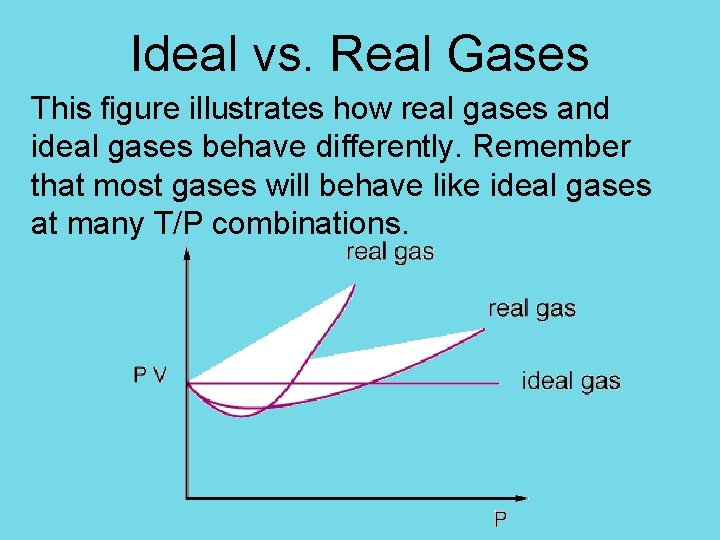
Ideal vs. Real Gases This figure illustrates how real gases and ideal gases behave differently. Remember that most gases will behave like ideal gases at many T/P combinations.

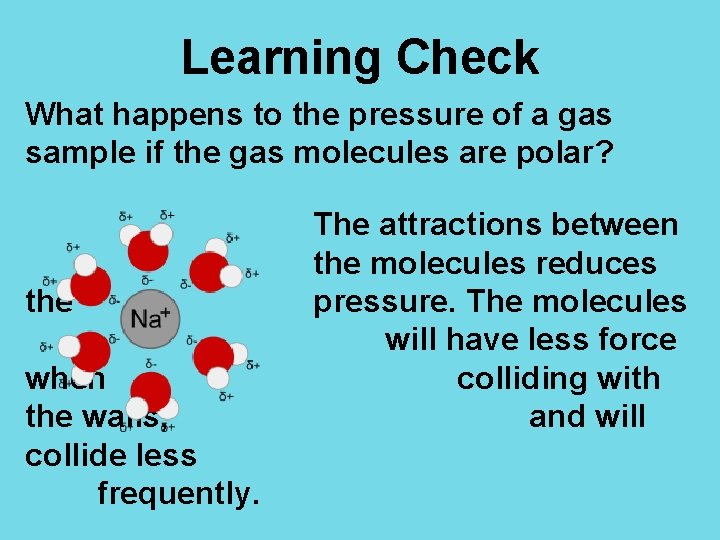
Learning Check What happens to the pressure of a gas sample if the gas molecules are polar? the when the walls, collide less frequently. The attractions between the molecules reduces pressure. The molecules will have less force colliding with and will

Main deviations of Real Gases Ideal gases: • Gas particles take up no space Bulky molecules • Gas particles have no intermolecular attractions Polar molecules • Gas particles have no attraction/repulsion with container walls • Collisions do not change the kinetic energy of the system Polar molecules • Ideal gases follow the gas laws for all T and P Extreme High pressure or low temperature

Avogadro’s Principle: equal volumes of gases at the same T and P contain an equal number of molecules or atoms This means there are the same number of gas molecules in 2. 0 L He gas, 2. 0 L H 2 gas, or 2. 0 L NH 3 gas at a particular P and T. We can use Avogadro’s Principle to solve stoichiometry problems for gases.

Gas Stoichiometry Whenever a gas is at STP we can use the molar volume of a gas to convert between liters of gas and moles of gas. Note the similarity to converting between grams and moles, as you learned in the stoichiometry unit. The molar volume of a gas is 22. 4 L/mole This means that 1 mole of any gas at STP has a volume of 22. 4 L.

Gas Stoichiometry Consider the following equation: 2 H 2 (g) + O 2 (g) 2 H 2 O (g) Calculate the number of moles of H 2 gas in a 2. 5 L sample of H 2 gas at STP. 2. 5 L H 2 (g) x = 0. 1116 mole H 2

Learning Check • If you have 6. 0 moles of O 2 gas, what will be the volume of the gas at STP? (6 mole O 2) x = 134. 4 L Remember, we can combine this with our knowledge of stoichiometry.

Learning Check Calculate the volume of 2000 g of methane (CH 4) gas at STP. Molar mass of CH 4 = 16. 042 g/mole (2000 g) x (124. 7 mole) x = 124. 7 mole CH 4 = 2793 L CH 4

Practice Work with a partner to solve problems 2024 from the book, page 453. Then, write a paragraph explaining why the volume of one mole of any gas is constant. Finally, write one question about something from this chapter that you are confused about.
 Pv=nrt density
Pv=nrt density Sutherland's law
Sutherland's law Ideal gas vs perfect gas
Ideal gas vs perfect gas Difference between ideal gas and real gas
Difference between ideal gas and real gas Imaginary gas
Imaginary gas Differences between ideal gas and real gas
Differences between ideal gas and real gas Charles de secondat
Charles de secondat Boyle's law example problem
Boyle's law example problem Conceptual gas law questions
Conceptual gas law questions Gas laws crash course
Gas laws crash course Units for pv=nrt
Units for pv=nrt Combined gas law worksheet
Combined gas law worksheet All the gas laws
All the gas laws Ap chemistry gas laws
Ap chemistry gas laws How to solve ideal gas law
How to solve ideal gas law Kmt gas laws
Kmt gas laws What is direct and indirect relationship
What is direct and indirect relationship Combined gas laws
Combined gas laws Chapter 13 gases
Chapter 13 gases Different gas laws
Different gas laws Gas laws graphic organizer
Gas laws graphic organizer Boyle's gas law formula
Boyle's gas law formula Gas law formula
Gas law formula Gas laws
Gas laws Solid volume definite or indefinite
Solid volume definite or indefinite Boyle's law states that
Boyle's law states that Charles law balloon
Charles law balloon Gas laws hot air balloon
Gas laws hot air balloon Different gas laws
Different gas laws Empirical gas laws
Empirical gas laws Comboned gas law
Comboned gas law Charles law formula
Charles law formula Ideal solution and non ideal solution
Ideal solution and non ideal solution Law of combining volumes
Law of combining volumes How to find density in ideal gas law
How to find density in ideal gas law Microcanonical ensemble ideal gas
Microcanonical ensemble ideal gas Pv=mrt
Pv=mrt Ideal gas law formula
Ideal gas law formula N/v=p/rt
N/v=p/rt Charles law
Charles law Classical ideal gas
Classical ideal gas Ide gas gif
Ide gas gif Gibbs-helmholtz equation
Gibbs-helmholtz equation Pzmore
Pzmore Boltzmann constant and gas constant
Boltzmann constant and gas constant Gases
Gases Constante r de los gases
Constante r de los gases Macroscopic description of an ideal gas
Macroscopic description of an ideal gas Ideal gas law powerpoint
Ideal gas law powerpoint