Gas Laws Chapter 10 Boyles Law The volume

Gas Laws Chapter 10

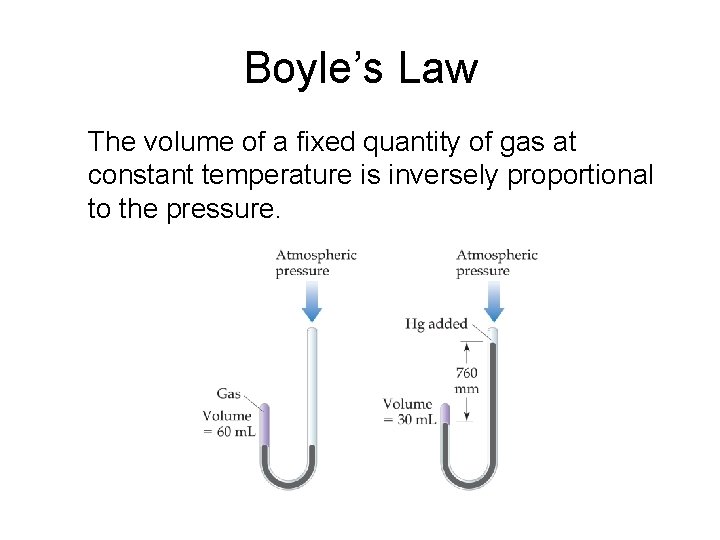
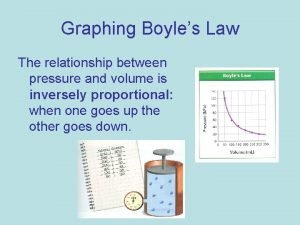
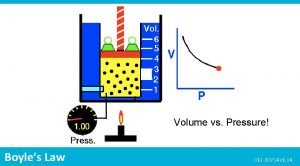
Boyle’s Law The volume of a fixed quantity of gas at constant temperature is inversely proportional to the pressure.

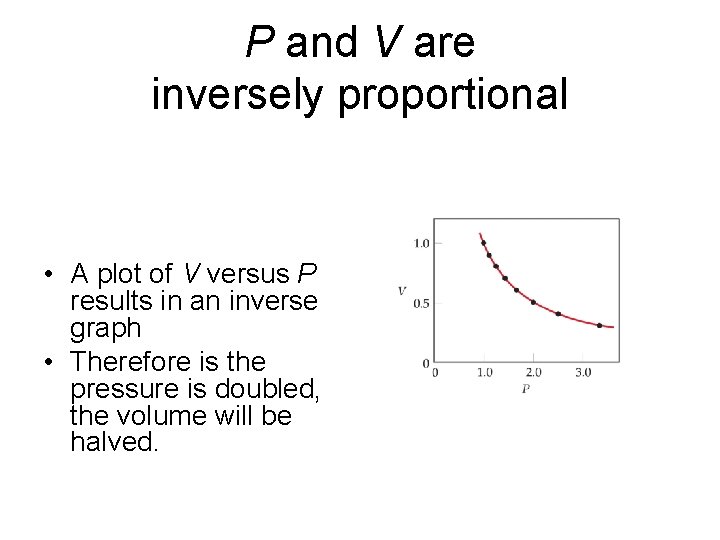
P and V are inversely proportional • A plot of V versus P results in an inverse graph • Therefore is the pressure is doubled, the volume will be halved.

Boyle’s Law Practice Problem • If I have 5. 6 liters of gas in a piston at a pressure of 1. 5 atm and compress the gas until its volume is 4. 8 L, what will the new pressure inside the piston be? P 1 V 1 = P 2 V 2 (1. 5 atm)(5. 6 L) = (x)(4. 8 L) x = 1. 8 atm

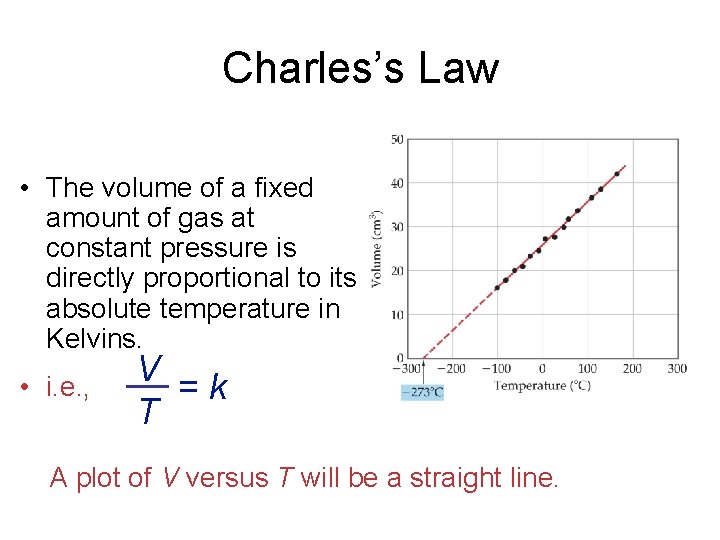
Charles’s Law • The volume of a fixed amount of gas at constant pressure is directly proportional to its absolute temperature in Kelvins. • i. e. , V = k T A plot of V versus T will be a straight line.

Charles’s Law Practice Problem • If I have 45 liters of helium in a balloon at 250 C and increase the temperature of the balloon to 550 C, what will the new volume of the balloon be?

Avogadro’s Law • The volume of a gas at constant temperature and pressure is directly proportional to the number of moles of the gas. • V 1/n 1 = V 2/n 2 • Mathematically, this means V = kn

Avagadro’s Law Practice Problem A 6. 0 L sample at 25 °C and 2. 00 atm of pressure contains 0. 5 moles of a gas. If an additional 0. 25 moles of gas at the same pressure and temperature added, what is the final total volume of the gas? Vf = (6. 0 L x 0. 75 moles)/0. 5 moles Vf = 4. 5 L/0. 5 Vf = 9 L

Ideal-Gas Equation • So far we’ve seen that V 1/P (Boyle’s law) V T (Charles’s law) V n (Avogadro’s law) • Combining these, we get n. T V P

Ideal-Gas Equation The constant of proportionality is known as R, the gas constant.

Ideal-Gas Equation The relationship n. T V P then becomes n. T V = R P or PV = n. RT

Ideal Gas Law Practice Problem • If I have 4 moles of a gas at a pressure of 5. 6 atm and a volume of 12 L, what is the temperature? PV=n. RT 205 K

Densities of Gases If we divide both sides of the ideal-gas equation by V and by RT, we get n P = V RT

Densities of Gases • We know that – moles molecular mass = mass n = m • So multiplying both sides by the molecular mass ( ) gives m P = V RT

Densities of Gases • Mass volume = density • So, m P d = = V RT • Note: One only needs to know the molecular mass, the pressure, and the temperature to calculate the density of a gas.

Molecular Mass We can manipulate the density equation to enable us to find the molecular mass of a gas: P d = RT Becomes d. RT = P