BOYLES LAW WJEC Physics Unit 1 1 8

BOYLE’S LAW WJEC Physics Unit 1 - 1. 8

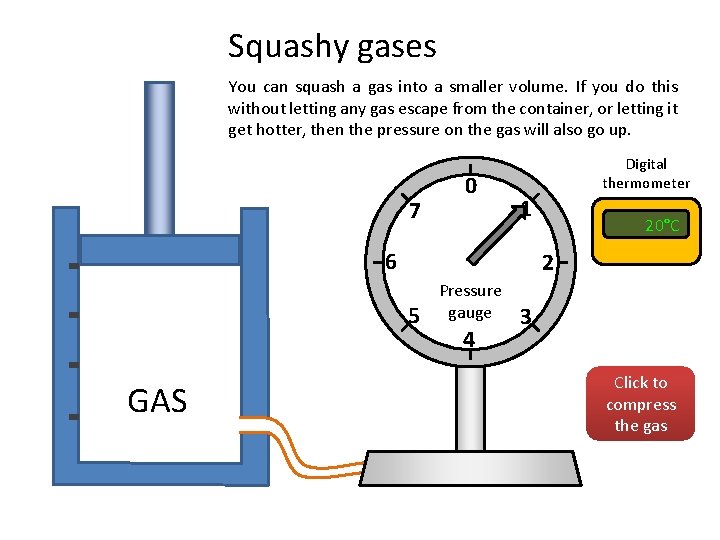
Squashy gases You can squash a gas into a smaller volume. If you do this without letting any gas escape from the container, or letting it get hotter, then the pressure on the gas will also go up. 7 0 Digital thermometer 1 6 2 5 GAS 20°C Pressure gauge 4 3 Click to compress the gas

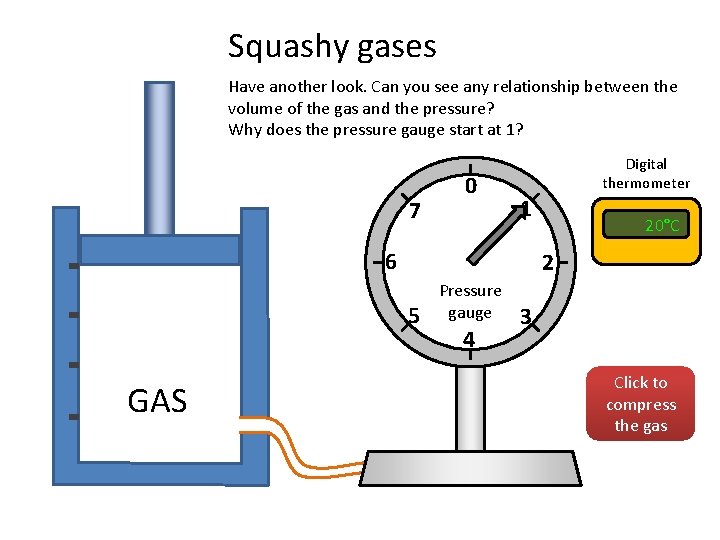
Squashy gases Have another look. Can you see any relationship between the volume of the gas and the pressure? Why does the pressure gauge start at 1? 7 0 Digital thermometer 1 6 2 5 GAS 20°C Pressure gauge 4 3 Click to compress the gas

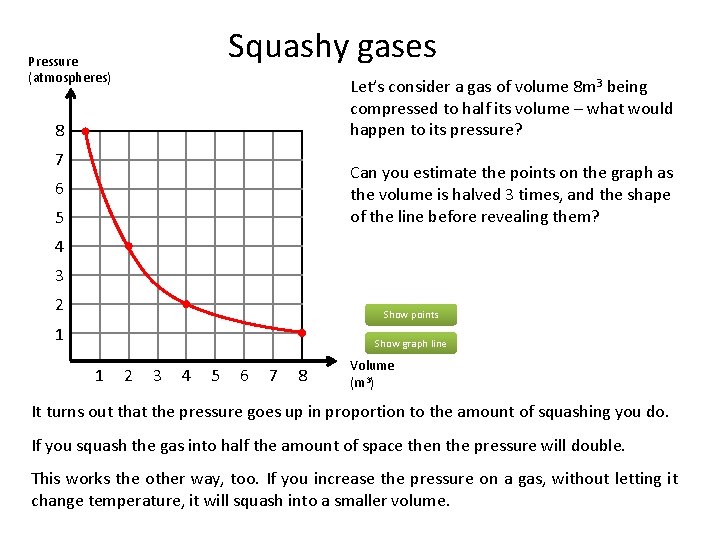
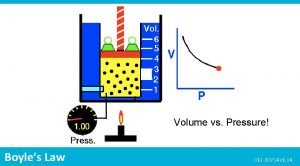
Squashy gases Pressure (atmospheres) Let’s consider a gas of volume 8 m 3 being compressed to half its volume – what would happen to its pressure? 8 7 Can you estimate the points on the graph as the volume is halved 3 times, and the shape of the line before revealing them? 6 5 4 3 2 Show points 1 Show graph line 1 2 3 4 5 6 7 8 Volume (m 3) It turns out that the pressure goes up in proportion to the amount of squashing you do. If you squash the gas into half the amount of space then the pressure will double. This works the other way, too. If you increase the pressure on a gas, without letting it change temperature, it will squash into a smaller volume.

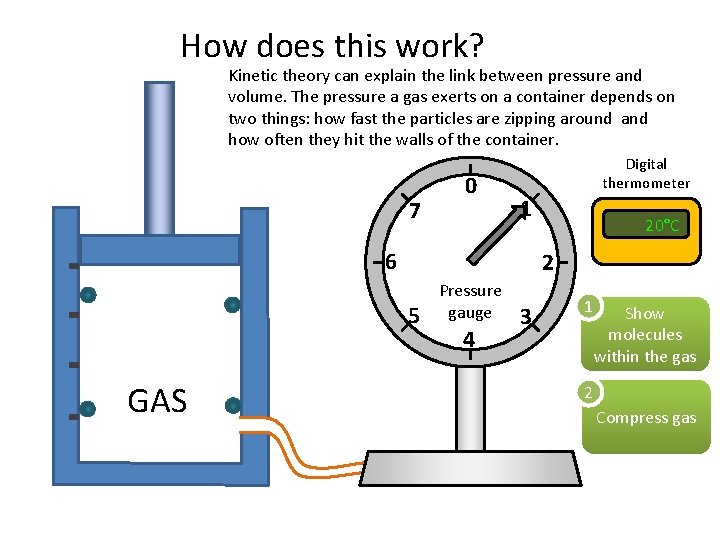
How does this work? Kinetic theory can explain the link between pressure and volume. The pressure a gas exerts on a container depends on two things: how fast the particles are zipping around and how often they hit the walls of the container. 7 0 Digital thermometer 1 6 2 5 GAS 20°C Pressure gauge 4 3 1 Show molecules within the gas 2 Compress gas

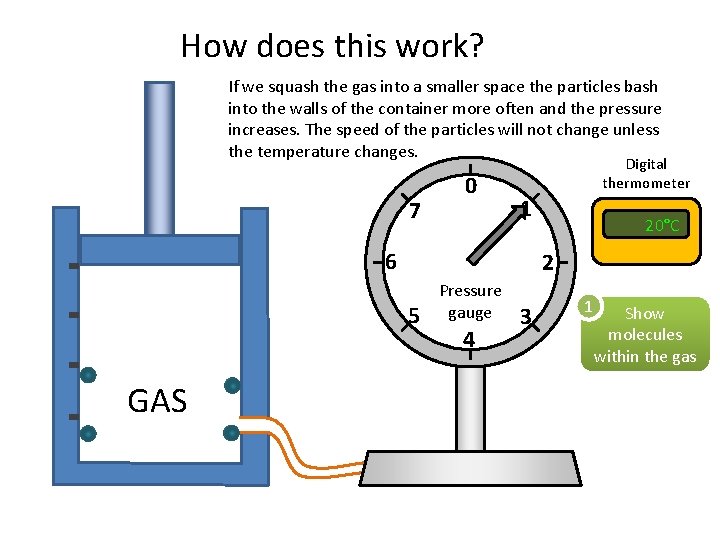
How does this work? If we squash the gas into a smaller space the particles bash into the walls of the container more often and the pressure increases. The speed of the particles will not change unless the temperature changes. 7 0 Digital thermometer 1 6 2 5 GAS 20°C Pressure gauge 4 3 1 Show molecules within the gas

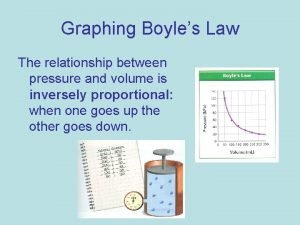
Boyle’s Law Boyle’s law sums up the link between the volume and pressure of a gas: “When the pressure is increased on a fixed mass of gas, kept at constant temperature, the volume will decrease. The changes in pressure and volume are in inverse proportion. ”

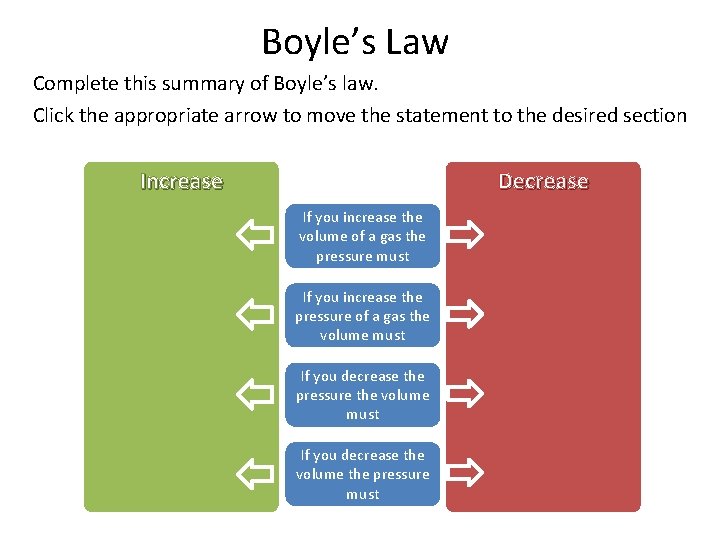
Boyle’s Law Complete this summary of Boyle’s law. Click the appropriate arrow to move the statement to the desired section Decrease Increase If you increase the volume of a gas the pressure must If you increase the pressure of a gas the volume must If you decrease the pressure the volume must If you decrease the volume the pressure must

Boyle’s law in Action TASK: • Click on the syringe on the following animation to change the volume of the gas inside the syringe. • Take at least 5 values of pressure and volume using the data in the animation. Click the image to access the activity. (Please note that this activity is flash based and may not work in some browsers) • Plot a suitable graph to represent your data.

The equation There is an equation to go with Boyle’s Law: p 1 V 1 = p 2 V 2 p 1 and V 1 are the pressure and volume of the gas at the start and p 2, V 2 are the final pressure and volume. Let’s look at an example: A gas starting off at a volume of 320 cm 3 and pressure of 2. 5 atmospheres is compressed down to a volume of 180 cm 3. What is the final pressure? V 1 = 320 cm 3 p 1 = 2. 5 atm p 1 V 1 = p 2 V 2 2. 5 x 320 = p 2 x 180 p 2 = (2. 5 x 320) 180 p 2 = 4. 4 atm V 2 = 180 cm 3

Solve these questions using the formula p 1 V 1 = p 2 V 2 1. A gas starting off at a volume of 2, 000 cm 3 and pressure of 5. 5 atmospheres is compressed down to a volume of 500 cm 3. What is the final pressure? 2. A gas in a volume of 550 cm 3 is compressed down to a new volume of 175 cm 3 and has a new pressure of 4. 7 atm. What was the initial pressure? 3. After compressing a gas from 700 cm 3 the pressure was found to have risen from 3 atm to 6 atm. What was the final volume? 4. A gas starts with a pressure of 2. 5 atmospheres and is compressed so that its final volume is one quarter of its initial volume. What is the final pressure of the gas? 5. In what volume did the gas at 3. 1 atm start if its final pressure is 4. 5 and its final volume is 600 cm 3?

Answers 1. 22 atm 2. 1. 5 atm 3. 350 cm 3 4. 10 atm 5. 871 cm 3