The Combined Gas Law Various Gas Laws Boyles

The Combined “Gas Law”

Various Gas Laws • Boyles Law: – initial pressure equals final pressure times final volume P 1 V 1 P 2 V 2 • Charles Law: – the ratio of volume to temperature of a given gas at fixed pressure is constant V 1/T 1 = V 2/T 2 • Gay-Lussac’s Law: – the ratio of pressure to temperature of a given gas at fixed volume is constant P 1/T 1 = P 2/ T 2 • Avogadro's Law: – at fixed pressure and temperature, the ratio of volume to moles (n) of a gas is constant V 1/n 1 V 2/n 2

• The Ideal Gas Law: – relates the amount of gas produced in a reaction PV=n. RT where • n= moles • R= 8. 31 L X k. Pa/mol x K – This is a constant number • Dalton’s Law of Partial Pressures: – the total pressure of a mixture of gases equals the sum of the pressures Ptotal= P 1+P 2 etc. • Combined Gas Law: – the combined law incorporates all of the laws: Boyles, Charles, Avogadro's, and Lussac’s P 1 V 1/n 1 T 1 = P 2 V 2/n 2 T 2 n= moles

Combining the gas laws Robert Boyle Jacques Charles V 1 V 2 = T 1 T 2 These are all subsets of a more encompassing law: the combined gas law P 1 V 1 = P 2 V 2 Joseph Louis Gay-Lussac P 1 T 1 P 2 = T 2 P 1 V 1 P 2 V 2 = T 1 T 2

Manipulating Variables in Equations • P 1 V 1 • T 1 P 2 V 2 T 2 P 1 V 1 T 2 = P 2 V 2 T 1 V 1 T 2 V 1 T 2 P 1 = P 2 V 2 T 1 V 1 T 2

Combined Gas Law Equations P 1 V 1 P 2 V 2 = T 1 T 2 P 2 V 2 T 1 P 1 = V 1 T 2 P 2 V 2 T 1 V 1 = P 1 T 2 P 2 V 2 T 1 = P 1 V 1 T 2 = P 2 V 2 T 1 P 1 V 1 T 2 P 2 = V 2 T 1 P 1 V 1 T 2 V 2 = P 2 T 1 P 1 V 1 T 2 = P 2 V 2

• What is the initial pressure of a system if the final volume is 250 ml. • Initial pressure (P 1)= 101 Kpa • Initial volume was 500 ml • All temperatures are at STP= 273 OK P 1 V 1 • P 1= ? T 1 • V 1= 250 mls P 1 V 1 T 2 • P 2= 101 k. Pa P 1 = • V 2= 500 ml *T 1 and T 2 are similar P 1 = (101 k. Pa)(250 mls) P 1 = 500 mls P 2 V 2 T 2 = P 2 V 2 T 1 V 1 T 2 P 2 V 2 V 1 = 50. 5 k. Pa

P 1 = 150 k. Pa, T 1 = 308 K P 2 = 250 k. Pa, T 2 = ? P 1 V 1 T 1 P 2 V 2 = T 2 V 1 = V 2 P 1 V 1 T 2 = P 2 V 2 T 1 = P 1 V 1 (250 k. Pa)(V 2)(308 K) (150 k. Pa)(V 1) = 513 K = 240 °C K at STP= 273, therefore, 513 K- 273= 240 OC Notice that V cancels out if V 1 = V 2 (T 2) =

P 1 = 100 k. Pa, V 1 = 5. 00 L, T 1 = 293 K P 2 = 90 k. Pa, V 2 = ? , T 2 = 308 K P 1 V 1 T 1 = P 2 V 2 T 2 P 1 V 1 T 2 = P 2 V 2 T 1 P 1 V 1 T 2 V 2 = P 2 T 1 (V 2) = (100 k. Pa)(5. 00 L)(308 K) = 5. 84 L (90 k. Pa)(293 K) Note: although k. Pa is used here, any unit for pressure will work, provided the same units are used throughout. The only unit that MUST be used is K for temperature.

P 1 = 800 k. Pa, V 1 = 1. 0 L, T 1 = 303 K P 2 = 100 k. Pa, V 2 = ? , T 2 = 298 K P 1 V 1 T 1 = P 2 V 2 T 2 P 1 V 1 T 2 V 2 = P 2 T 1 (V 2) = (800 k. Pa)(1. 0 L)(298 K) (100 k. Pa)(303 K) = 7. 9 L
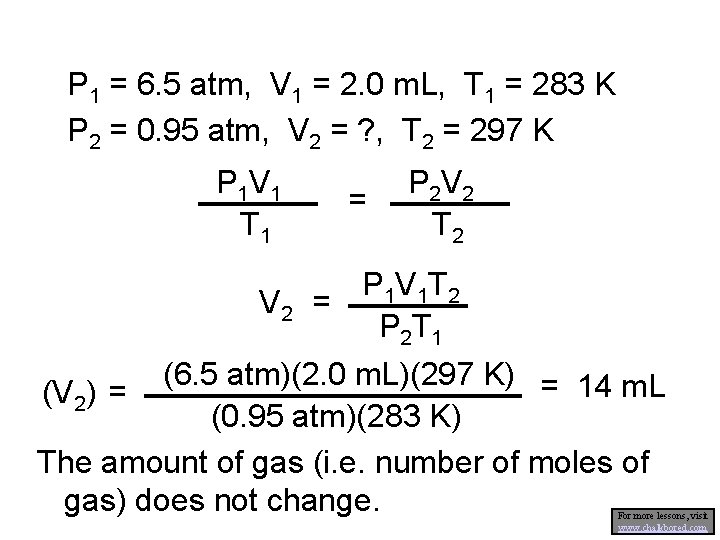
P 1 = 6. 5 atm, V 1 = 2. 0 m. L, T 1 = 283 K P 2 = 0. 95 atm, V 2 = ? , T 2 = 297 K P 1 V 1 T 1 = P 2 V 2 T 2 P 1 V 1 T 2 V 2 = P 2 T 1 (6. 5 atm)(2. 0 m. L)(297 K) = 14 m. L (V 2) = (0. 95 atm)(283 K) The amount of gas (i. e. number of moles of gas) does not change. For more lessons, visit www. chalkbored. com
- Slides: 11