Classical Ideal Gas In our review of undergrad




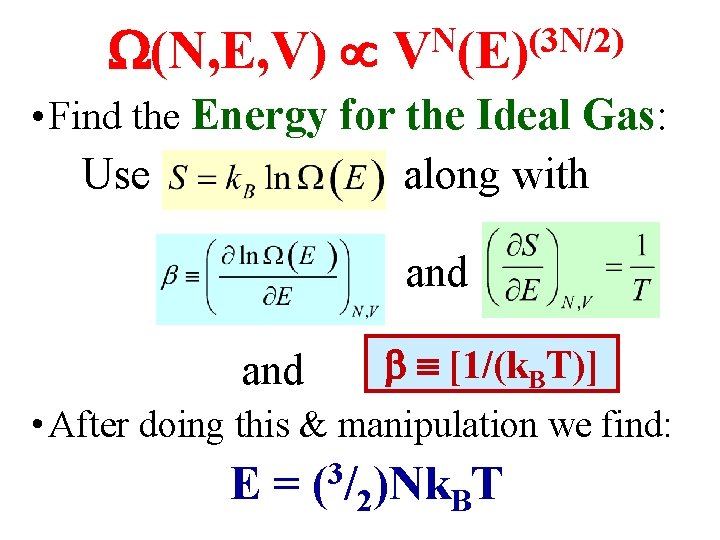













- Slides: 20

Classical Ideal Gas

• In our review of undergrad Statistical & Thermal Physics, we looked briefly at the Classical Ideal Gas with N particles & volume V. We calculated the E & V dependences of the number of accessible states (N, E, V) for such a gas. We found: (N, E, V) N (3 N/2) V (E)

(N, E, V) N (3 N/2) V (E) • Using the general form for the pressure that we just talked about, the Equation of State (or P, T, V relation) can be obtained for the Classical Ideal Gas: p = k. BT[∂ln( )/∂V] • So, we have simply PV = Nk. BT

(N, E, V) N (3 N/2) V (E) • The Entropy for the Ideal Gas: S = k. B ln = N ln(V) + (3/2)N ln(E) + const S 0 = k. B ln 0 = N ln(V 0) + (3/2)N ln(E 0) + const S = S – S 0 = N ln(V/V 0) + (3/2)N ln(E/E 0)
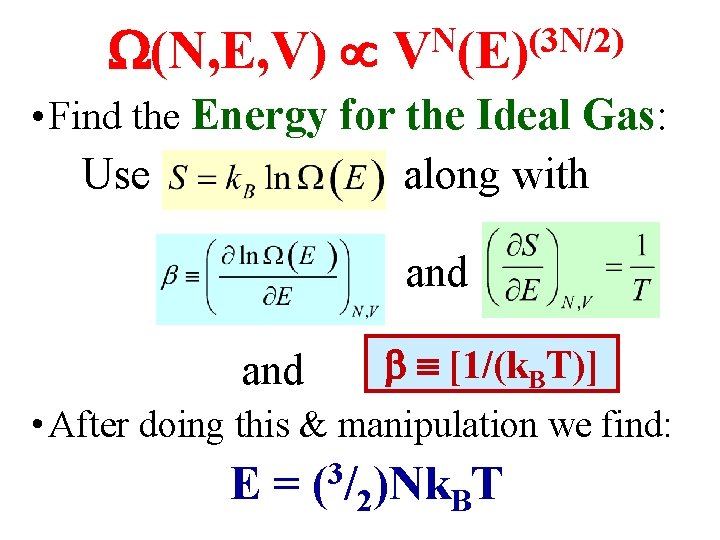
(N, E, V) N (3 N/2) V (E) • Find the Energy for the Ideal Gas: Use along with l and [1/(k. BT)] • After doing this & manipulation we find: E = (3/2)Nk. BT

Gibbs’ Paradox: Entropy of Mixing

• Entropy for the Classical Ideal Gas: S = k. B ln = N ln(V) + (3/2)N ln(E) + const • For N non-interacting molecules the energy E = N , where = energy of one molecule. • In what follows, the references I used assume that each molecule is a quantum mechanical particle in a box, which introduces Planck’s Constant ħ into the otherwise classical expressions. This affects the entropy by only a constant.

Entropy in the Ideal Gas • Consider an Ideal, Monatomic Gas with N molecules in volume V & with mean energy U. • From earlier discussions, the Entropy is (E U)

Entropy in the Ideal Gas • As first pointed out by Gibbs, this Entropy is WRONG! • Specifically, its dependence on particle number N is wrong! Gibbs’ Paradox! • To see that this S is wrong, consider the Mixing of 2 Ideal Gases

Entropy in the Ideal Gas • The Boltzmann Definition of Entropy is • Ideal Gas Entropy in the Canonical Ensemble: “Sackur-Tetrode” Equation

Entropy in the Ideal Gas • Expand the log function (f degrees of freedom for polyatomic molecules) • Use equipartition of energy: U = (½)f k. BT

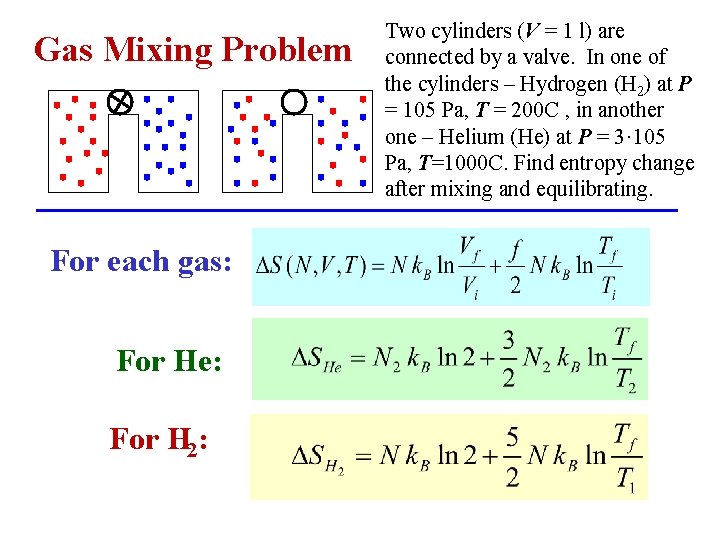
Gas Mixing Problem For each gas: For He: For H 2: Two cylinders (V = 1 l) are connected by a valve. In one of the cylinders – Hydrogen (H 2) at P = 105 Pa, T = 200 C , in another one – Helium (He) at P = 3· 105 Pa, T=1000 C. Find entropy change after mixing and equilibrating.

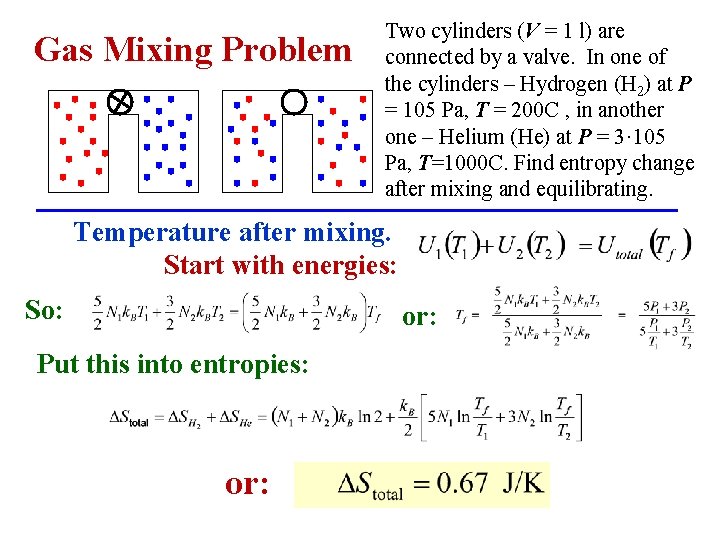
Gas Mixing Problem Two cylinders (V = 1 l) are connected by a valve. In one of the cylinders – Hydrogen (H 2) at P = 105 Pa, T = 200 C , in another one – Helium (He) at P = 3· 105 Pa, T=1000 C. Find entropy change after mixing and equilibrating. Temperature after mixing. Start with energies: So: or: Put this into entropies: or:

Gas Mixing Problem Two cylinders (V = 1 l) are connected by a valve. In one of the cylinders – Hydrogen (H 2) at P = 105 Pa, T = 200 C , in another one – Helium (He) at P = 3· 105 Pa, T=1000 C. Find entropy change after mixing and equilibrating. if N 1=N 2=1/2 N V 1=V 2=1/2 V The total entropy of the system is greater after mixing – thus, mixing is irreversible.

Gibbs Paradox - applies only if two gases are different ! If two mixing gases are of the same kind (indistinguishable molecules): Stotal = 0 because U/N and V/N available for each molecule remain the same after mixing. Quantum-mechanical indistinguishability is important! (even though this equation applies only in the low density limit, which is “classical” in the sense that the distinction between fermions and bosons disappear.

Gibbs Paradox Two identical perfect gases with the same pressure P and the same number of particles N, but with different temperatures T 1 and T 2, are confined in two vessels, of volume V 1 and V 2 , which are then connected. find the change in entropy after the system has reached equilibrium. - prove it! at T 1=T 2, S=0, as it should be (Gibbs paradox)

Ideal Gas: from S(N, V, U) - to U(N, V, T) Ideal gas: (f. N degrees of freedom) - the “energy” equation of state in agreement with the equipartition theorem, the total energy should be ½k. BT times the number of degrees of freedom. - The heat capacity for a monatomic ideal gas:

“Pressure” Equation of State for an Ideal Gas The “energy” equation of state (U T): Ideal gas: (f. N degrees of freedom) The “pressure” equation of state (P T): - we have finally derived the equation of state of an ideal gas from first principles!

A Perhaps Simpler Explanation of Gibbs’ Paradox? • If N molecules of an ideal monatomic gas make a free expansion from V to 2 V, ΔE = 0, so that ΔS = Sf – Si = Nk. B ln(2 V/V) = Nk. B ln 2 (1) • If the container of volume 2 V is divided into equal parts, so that (N/2) molecules are in each half, then ΔS' = Sf' – Si' = 2(N/2)k. Bln(V/2 V) = – Nk. Bln 2 (2) This is Gibbs’ Paradox 19

Gibbs’ Paradox • Gibbs’ Paradox, is removed by assuming that the molecules are indistinguishable; i. e. that the number of accessible states is (E, V, N) = B U 3 N/2 VN/N! • This means that term Nk. Bln. V in the expression for S is replaced by Nk. B ln(V/N!), • In the latter expression, use Stirling’s Formula: Nk. B ln(V/N!) ≈ Nk. B [ln(V/N) + 1] 20
 Classical ideal gas
Classical ideal gas Ideal gas vs perfect gas
Ideal gas vs perfect gas An ideal gas is an imaginary gas
An ideal gas is an imaginary gas Differences between ideal gas and real gas
Differences between ideal gas and real gas Ideal gas vs perfect gas
Ideal gas vs perfect gas Difference between ideal gas and real gas
Difference between ideal gas and real gas Cluster expansion for a classical gas
Cluster expansion for a classical gas Cluster expansion for a classical gas
Cluster expansion for a classical gas Ideal solution and non ideal solution
Ideal solution and non ideal solution Real self description
Real self description Thinking affects our language, which then affects our:
Thinking affects our language, which then affects our: Our census our future
Our census our future Words to christ be our light
Words to christ be our light Our life is what our thoughts make it
Our life is what our thoughts make it We bow our hearts
We bow our hearts Our census our future
Our census our future Our life is what our thoughts make it
Our life is what our thoughts make it Money is our madness our vast
Money is our madness our vast Awareness of ourselves and our environment is:
Awareness of ourselves and our environment is: Is our awareness of ourselves and our environment.
Is our awareness of ourselves and our environment. God our father christ our brother
God our father christ our brother