10 The Method of Cluster Expansions 1 Cluster










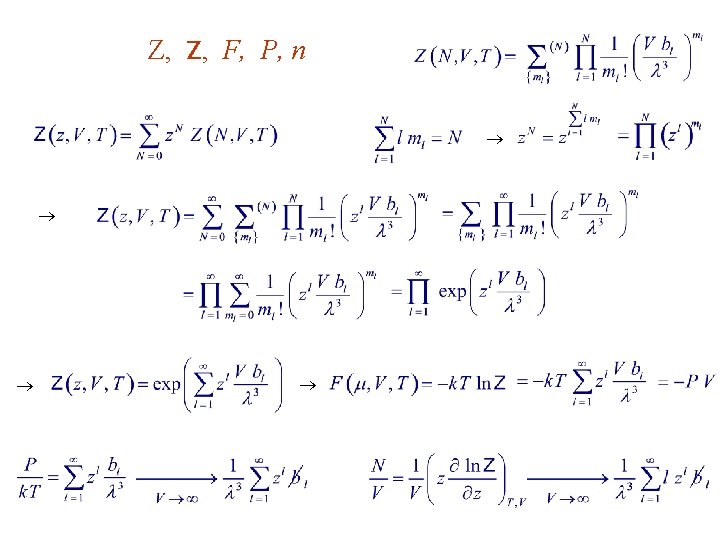




















- Slides: 35

10. The Method of Cluster Expansions 1. Cluster Expansion for a Classical Gas 2. Virial Expansion of the Equation of State 3. Evaluation of the Virial Coefficients 4. General Remarks on Cluster Expansions 5. Exact Treatment of the Second Virial Coefficient 6. Cluster Expansion for a Quantum Mechanical System 7. Correlations & Scattering

Cluster expansions = Series expansion to handle inter-particle interactions Applicability : Low density gases Poineers : Mayer : Classical statistics. Kahn-Uhlenbeck, Lee-Yang : Quantum statistics

10. 1. Cluster Expansion for a Classical Gas Central forces : Partition function :

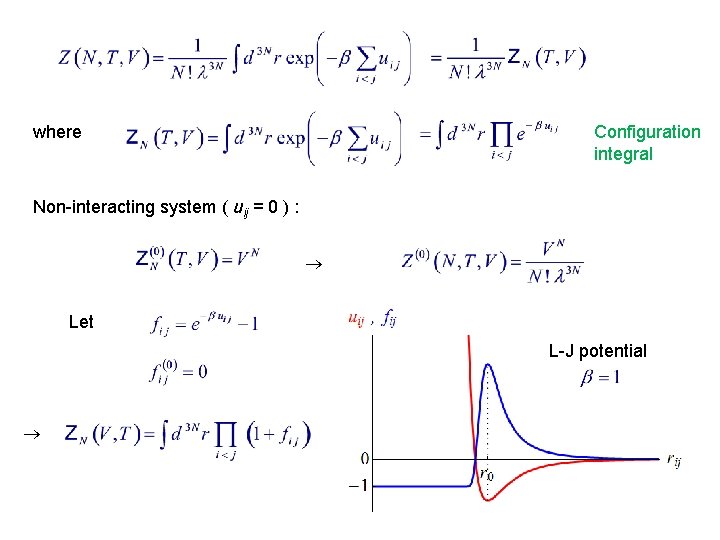
where Configuration integral Non-interacting system ( uij = 0 ) : Let L-J potential

Graphic Expansion All possible pairings 8 -particle graphs : = = factorized = =

l - Cluster Each N-particle integral is represented by an N-particle graph. Graphs of the same topology but different labellings are counted as distinct. An l-cluster graph is a connected l-particle graph. ( Integral cannot be factorized. ) E. g. , 5 -cluster : = Integrals represented by l-clusters of the same topology has the same value. All possible 3 -clusters : = =

Cluster Integrals Cluster integral : Let = dimension of X. X is dimensionless ru = range of u For a fixed r 1 , is indep of V. is indep of size & shape of system

Examples V(r 1) = volume of gas using r 1 as origin.


ZN Let ml = # of l-cluster graphs Let for each N-particle graph be the sum of all graphs that satisfy # of distinct ways to assign particles into is Let there be pl distinct ways to form an l-cluster, with each giving an integral Il j. Then the sum of all distinct products of ml of these l-clusters is The factor ml ! arises because the order of Il j within each product is immaterial.

where
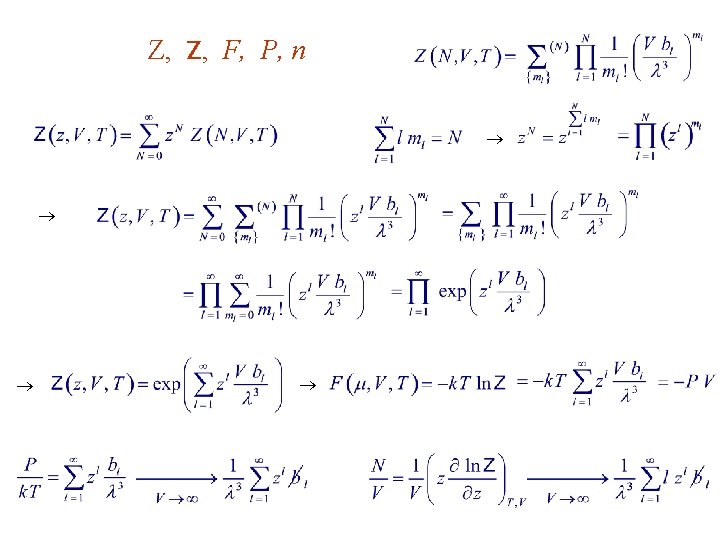
Z, Z, F, P, n

10. 2. Virial Expansion of the Equation of State Virial expansion for gases : Invert gives Mathematica

In general : (see § 10. 4 for proof ) irreducible cluster integral ( dimensionless ) Irreducible means multiply-connected, i. e. , more than one path connecting any two vertices. c. f.

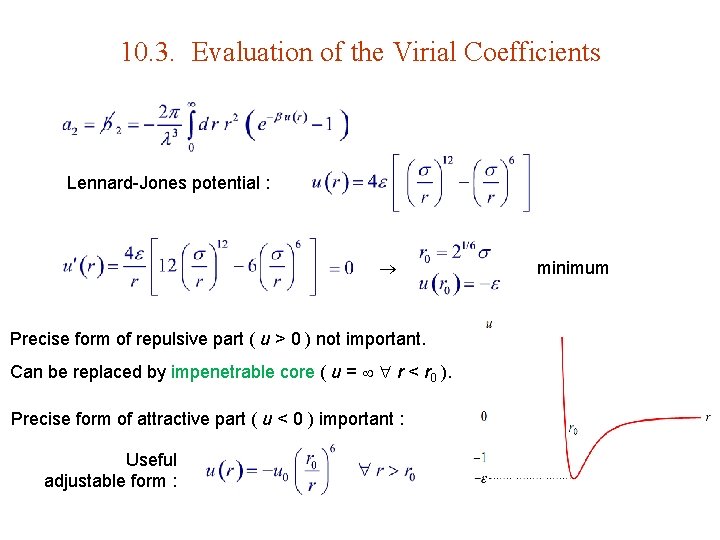
10. 3. Evaluation of the Virial Coefficients Lennard-Jones potential : Precise form of repulsive part ( u > 0 ) not important. Can be replaced by impenetrable core ( u = r < r 0 ). Precise form of attractive part ( u < 0 ) important : Useful adjustable form : minimum

a 2 For : Bl are also called the virial coefficients

van der Waals Equation for c. f. van der Waals eq. v 0 = molecular volume see Prob 1. 4 Condition r 0 = molecular diameter ( dilute gas )

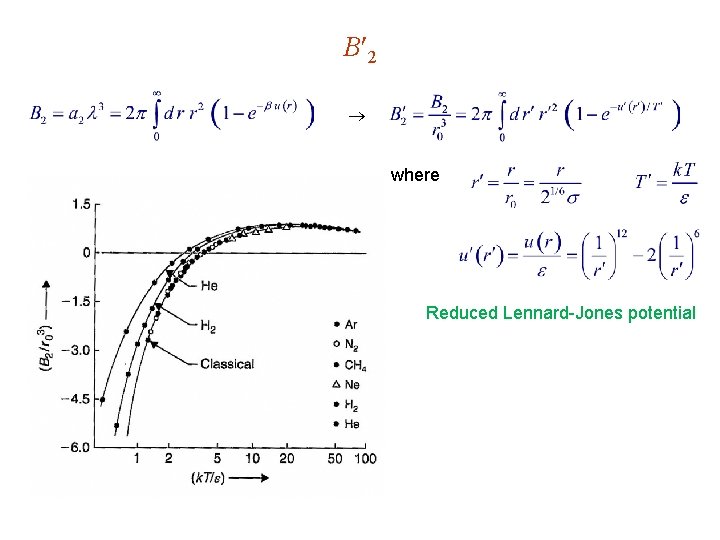
B 2 where Reduced Lennard-Jones potential

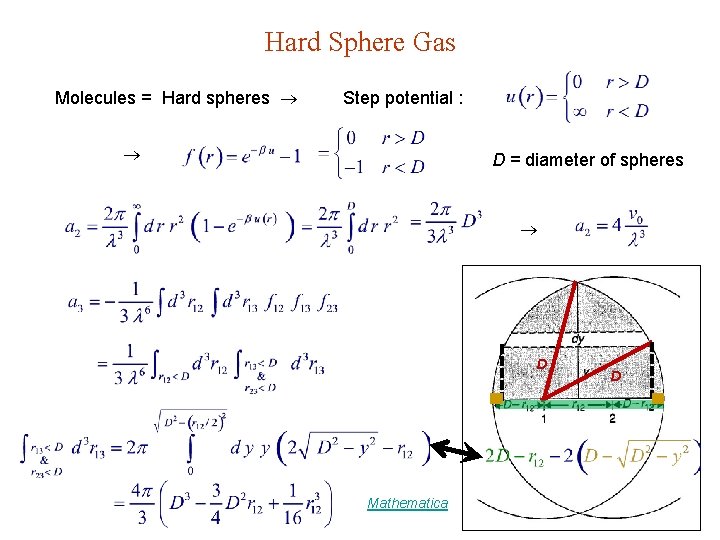
Hard Sphere Gas Molecules = Hard spheres Step potential : D = diameter of spheres D Mathematica D

Mathematica See Pathria, p. 314 for values of a 4 , a 5 , a 6 & P. Approximate analytic form of the equation of state for fluids ( : )

10. 4. General Remarks on Cluster Expansions Cluster Expansion :

Coefficients of Zjk in (. . . )l sum to 0. Classical ideal gas : (. . . )l ~ sum of all possible l-clusters are independent of V (. . . )l V Rushbrooke :

Semi-Invariants Constraint (l ) : Semi-Invariants Inversion :

Proof of inversion QED

A theorem due to Lagrange : Solution x(z) to eq. where is

constraint (j 1) : Inversion due to Mayer : constraint (l 1) :

10. 5. Exact Treatment of the Second Virial Coefficient u(r) = 0 where Total Let Reduced


Let spectrum of interacting system consist of a discrete (bounded states) part & a continuum (travelling states) part with DOS g( ).

Unbounded states ( n > 0 ) where l = phase shift

For the purpose of counting states ( to get g( ) ), we discretize the spectrum by setting for some . k l m is 2 l+1 fold degenerate For a given l , e/o means l in sum is even/odd for boson/fermion For u = 0 :

From § 7. 1 & § 8. 1 : Boson Fermion

b 2(0) From § 5. 5 : Alternatively, using the statistical potential from § 5. 5 same as before

Hard Sphere Gas In region where u = 0, Mathematica

1. No bound states for hard sphere gas. 2. Mathematica
 Lesson 9 decimal expansions of fractions
Lesson 9 decimal expansions of fractions Half-range expansions
Half-range expansions Method method method
Method method method Hình ảnh bộ gõ cơ thể búng tay
Hình ảnh bộ gõ cơ thể búng tay Lp html
Lp html Bổ thể
Bổ thể Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Voi kéo gỗ như thế nào
Voi kéo gỗ như thế nào Thang điểm glasgow
Thang điểm glasgow Hát lên người ơi alleluia
Hát lên người ơi alleluia Các môn thể thao bắt đầu bằng tiếng chạy
Các môn thể thao bắt đầu bằng tiếng chạy Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Công thức tính độ biến thiên đông lượng
Công thức tính độ biến thiên đông lượng Trời xanh đây là của chúng ta thể thơ
Trời xanh đây là của chúng ta thể thơ Mật thư anh em như thể tay chân
Mật thư anh em như thể tay chân 101012 bằng
101012 bằng độ dài liên kết
độ dài liên kết Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Thể thơ truyền thống
Thể thơ truyền thống Quá trình desamine hóa có thể tạo ra
Quá trình desamine hóa có thể tạo ra Một số thể thơ truyền thống
Một số thể thơ truyền thống Cái miệng nó xinh thế chỉ nói điều hay thôi
Cái miệng nó xinh thế chỉ nói điều hay thôi Vẽ hình chiếu vuông góc của vật thể sau
Vẽ hình chiếu vuông góc của vật thể sau Nguyên nhân của sự mỏi cơ sinh 8
Nguyên nhân của sự mỏi cơ sinh 8 đặc điểm cơ thể của người tối cổ
đặc điểm cơ thể của người tối cổ Ví dụ giọng cùng tên
Ví dụ giọng cùng tên Vẽ hình chiếu đứng bằng cạnh của vật thể
Vẽ hình chiếu đứng bằng cạnh của vật thể Tia chieu sa te
Tia chieu sa te Thẻ vin
Thẻ vin đại từ thay thế
đại từ thay thế điện thế nghỉ
điện thế nghỉ Tư thế ngồi viết
Tư thế ngồi viết Diễn thế sinh thái là
Diễn thế sinh thái là Dạng đột biến một nhiễm là
Dạng đột biến một nhiễm là Các số nguyên tố là gì
Các số nguyên tố là gì



























































