Cluster Analysis Cluster Analysis p What is Cluster

Cluster Analysis

Cluster Analysis p What is Cluster Analysis? p Types of Data in Cluster Analysis p A Categorization of Major Clustering Methods p Partitioning Methods p Hierarchical Methods p Density-Based Methods p Grid-Based Methods p Subspace Clustering/Bi-clustering p Model-Based Clustering

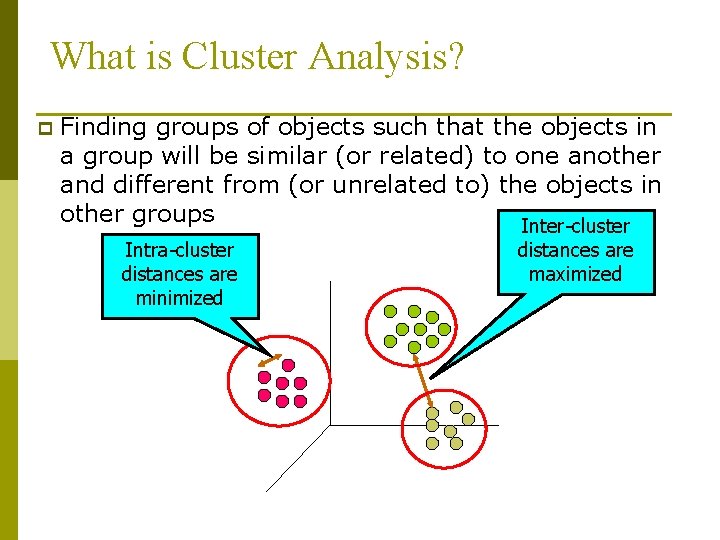
What is Cluster Analysis? p Finding groups of objects such that the objects in a group will be similar (or related) to one another and different from (or unrelated to) the objects in other groups Inter-cluster Intra-cluster distances are minimized distances are maximized

What is Cluster Analysis? p Cluster: a collection of data objects n n p Cluster analysis n p p Similar to one another within the same cluster Dissimilar to the objects in other clusters Grouping a set of data objects into clusters Clustering is unsupervised classification: no predefined classes Clustering is used: n As a stand-alone tool to get insight into data distribution p n Visualization of clusters may unveil important information As a preprocessing step for other algorithms p Efficient indexing or compression often relies on clustering

Some Applications of Clustering p p Pattern Recognition Image Processing n p p cluster images based on their visual content Bio-informatics WWW and IR n n document classification cluster Weblog data to discover groups of similar access patterns

What Is Good Clustering? p A good clustering method will produce high quality clusters with n high intra-class similarity n low inter-class similarity p The quality of a clustering result depends on both the similarity measure used by the method and its implementation. p The quality of a clustering method is also measured by its ability to discover some or all of the hidden patterns.

Requirements of Clustering in Data Mining p Scalability p Ability to deal with different types of attributes p Discovery of clusters with arbitrary shape p Minimal requirements for domain knowledge to determine input parameters p Able to deal with noise and outliers p Insensitive to order of input records p High dimensionality p Incorporation of user-specified constraints p Interpretability and usability

Outliers p Outliers are objects that do not belong to any cluster or form clusters of very small cardinality cluster outliers p In some applications we are interested in discovering outliers, not clusters (outlier analysis)

Data Structures n (two modes) the “classic” data input p tuples/objects data matrix dissimilarity or distance matrix n (one mode) Assuming simmetric distance d(i, j) = d(j, i) objects p attributes/dimensions objects

Measuring Similarity in Clustering p Dissimilarity/Similarity metric: n n n The dissimilarity d(i, j) between two objects i and j is expressed in terms of a distance function, which is typically a metric: metric d(i, j) 0 (non-negativity) d(i, i)=0 (isolation) d(i, j)= d(j, i) (symmetry) d(i, j) ≤ d(i, h)+d(h, j) (triangular inequality) p The definitions of distance functions are usually different for interval-scaled, boolean, categorical, ordinal and ratio-scaled variables. p Weights may be associated with different variables based on applications and data semantics.

Type of data in cluster analysis p Interval-scaled variables n p Binary variables n p e. g. , military rank (soldier, sergeant, lutenant, captain, etc. ) Ratio-scaled variables n p e. g. , religion (Christian, Muslim, Buddhist, Hindu, etc. ) Ordinal variables n p e. g. , gender (M/F), has_cancer(T/F) Nominal (categorical) variables n p e. g. , salary, height population growth (1, 100, 1000, . . . ) Variables of mixed types n multiple attributes with various types

Similarity and Dissimilarity Between Objects p Distance metrics are normally used to measure the similarity or dissimilarity between two data objects p The most popular conform to Minkowski distance: where i = (xi 1, xi 2, …, xin) and j = (xj 1, xj 2, …, xjn) are two n-dimensional data objects, and p is a positive integer p If p = 1, L 1 is the Manhattan (or city block) distance:

Similarity and Dissimilarity Between Objects (Cont. ) p If p = 2, L 2 is the Euclidean distance: n p Properties p d(i, j) 0 p d(i, i) =0 p d(i, j) = d(j, i) p d(i, j) d(i, k) + d(k, j) Also one can use weighted distance:

Binary Variables p A binary variable has two states: 0 absent, 1 present p A contingency table for binary data object j i= (0011101001) J=(100110) p object i Simple matching coefficient distance (invariant, if the binary variable is symmetric): p Jaccard coefficient distance (noninvariant if the binary variable is asymmetric):

Binary Variables p Another approach is to define the similarity of two objects and not their distance. p In that case we have the following: n Simple matching coefficient similarity: n Jaccard coefficient similarity: Note that: s(i, j) = 1 – d(i, j)

Dissimilarity between Binary Variables p Example (Jaccard coefficient) n n n all attributes are asymmetric binary 1 denotes presence or positive test 0 denotes absence or negative test

A simpler definition p Each variable is mapped to a bitmap (binary vector) n n n Jack: Mary: Jim: 101000 101010 110000 p Simple match distance: p Jaccard coefficient:

Variables of Mixed Types p A database may contain all the six types of variables n p symmetric binary, asymmetric binary, nominal, ordinal, interval and ratio-scaled. One may use a weighted formula to combine their effects.

Major Clustering Approaches p Partitioning algorithms: Construct random partitions and then iteratively refine them by some criterion p Hierarchical algorithms: Create a hierarchical decomposition of the set of data (or objects) using some criterion p Density-based: based on connectivity and density functions p Grid-based: based on a multiple-level granularity structure p Model-based: A model is hypothesized for each of the clusters and the idea is to find the best fit of that model to each other

Partitioning Algorithms: Basic Concept p Partitioning method: Construct a partition of a database D of n objects into a set of k clusters n k-means (Mac. Queen’ 67): Each cluster is represented by the center of the cluster n k-medoids or PAM (Partition around medoids) (Kaufman & Rousseeuw’ 87): Each cluster is represented by one of the objects in the cluster

K-means Clustering p p p Partitional clustering approach Each cluster is associated with a centroid (center point) Each point is assigned to the cluster with the closest centroid Number of clusters, K, must be specified The basic algorithm is very simple

K-means Clustering – Details p Initial centroids are often chosen randomly. n p p p The centroid is (typically) the mean of the points in the cluster. ‘Closeness’ is measured by Euclidean distance, cosine similarity, correlation, etc. Most of the convergence happens in the first few iterations. n p Clusters produced vary from one run to another. Often the stopping condition is changed to ‘Until relatively few points change clusters’ Complexity is O( n * K * I * d ) n n = number of points, K = number of clusters, I = number of iterations, d = number of attributes

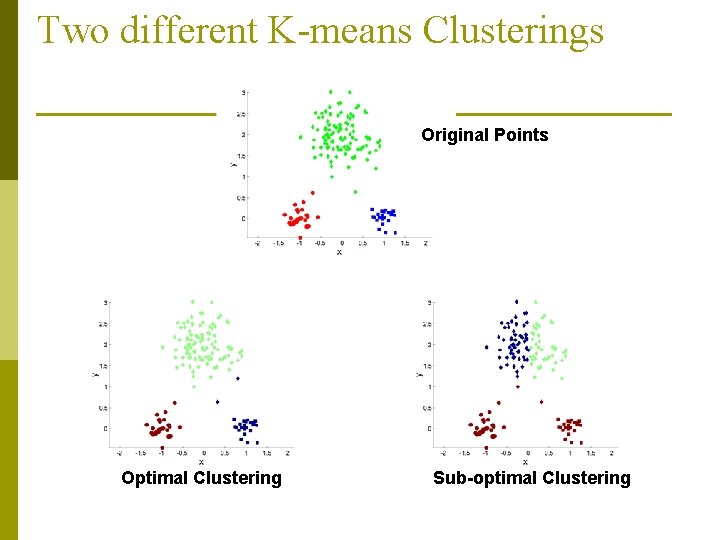
Two different K-means Clusterings Original Points Optimal Clustering Sub-optimal Clustering

Evaluating K-means Clusters n n n For each point, the error is the distance to the nearest cluster To get SSE, we square these errors and sum them. x is a data point in cluster Ci and mi is the representative point for cluster Ci can show that mi corresponds to the center (mean) of the cluster p n Given two clusters, we can choose the one with the smallest error

Solutions to Initial Centroids Problem p Multiple n runs Helps, but probability is not on your side p Sample and use hierarchical clustering to determine initial centroids p Select more than k initial centroids and then select among these initial centroids n Select most widely separated p Postprocessing p Bisecting n K-means Not as susceptible to initialization issues

Limitations of K-means p K-means has problems when clusters are of differing n n n Sizes Densities Non-spherical shapes p K-means has problems when the data contains outliers. Why?

The K-Medoids Clustering Method p Find representative objects, called medoids, in clusters p PAM (Partitioning Around Medoids, 1987) n starts from an initial set of medoids and iteratively replaces one of the medoids by one of the non-medoids if it improves the total distance of the resulting clustering n PAM works effectively for small data sets, but does not scale well for large data sets p CLARA (Kaufmann & Rousseeuw, 1990) p CLARANS (Ng & Han, 1994): Randomized sampling

PAM (Partitioning Around Medoids) (1987) p PAM (Kaufman and Rousseeuw, 1987), built in statistical package S+ p Use a real object to represent the a cluster 1. Select k representative objects arbitrarily 2. For each pair of a non-selected object h and a selected object i, calculate the total swapping cost TCih 3. For each pair of i and h, p p 4. If TCih < 0, i is replaced by h Then assign each non-selected object to the most similar representative object repeat steps 2 -3 until there is no change

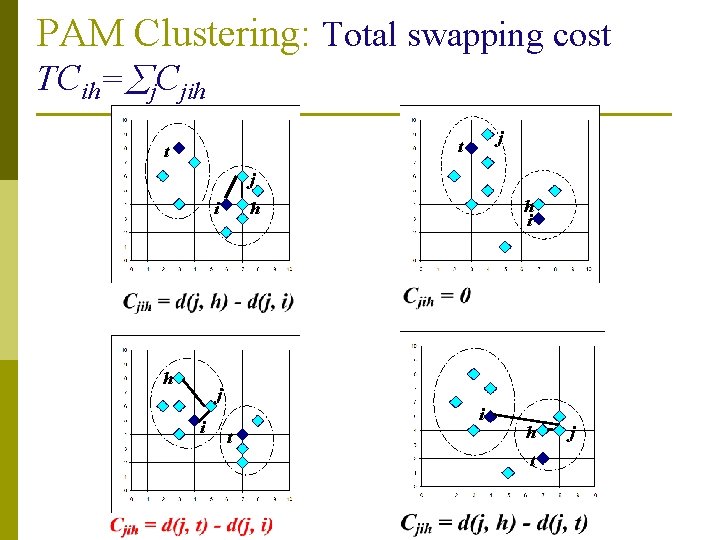
PAM Clustering: Total swapping cost TCih= j. Cjih pi is a current medoid, h is a nonselected object p Assume that i is replaced by h in the set of medoids p TCih = 0; p For each non-selected object j ≠ h: n TCih += d(j, new_medj)-d(j, prev_medj): p new_medj = the closest medoid to j after i is replaced by h p prev_medj = the closest medoid to j before i is replaced by h

PAM Clustering: Total swapping cost TCih= j. Cjih j t t j i h i h i t h t j

CLARA (Clustering Large Applications) p CLARA (Kaufmann and Rousseeuw in 1990) n Built in statistical analysis packages, such as S+ p It draws multiple samples of the data set, applies PAM on each sample, and gives the best clustering as the output p Strength: deals with larger data sets than PAM p Weakness: n Efficiency depends on the sample size n A good clustering based on samples will not necessarily represent a good clustering of the whole data set if the sample is biased

CLARANS (“Randomized” CLARA) p CLARANS (A Clustering Algorithm based on Randomized Search) (Ng and Han’ 94) p CLARANS draws sample of neighbors dynamically p The clustering process can be presented as searching a graph where every node is a potential solution, that is, a set of k medoids p If the local optimum is found, CLARANS starts with new randomly selected node in search for a new local optimum p It is more efficient and scalable than both PAM and CLARA p Focusing techniques and spatial access structures may further improve its performance (Ester et al. ’ 95)

Cluster Analysis p What is Cluster Analysis? p Types of Data in Cluster Analysis p A Categorization of Major Clustering Methods p Partitioning Methods p Hierarchical Methods p Density-Based Methods p Grid-Based Methods p Model-Based Clustering Methods p Outlier Analysis p Summary

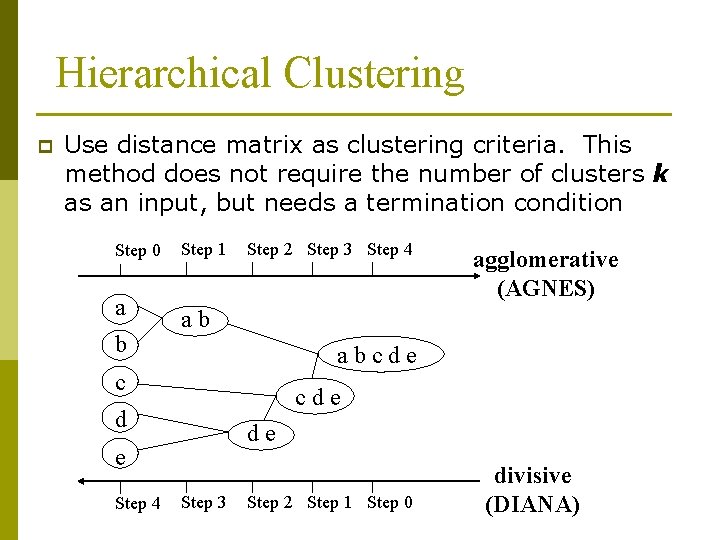
Hierarchical Clustering p Use distance matrix as clustering criteria. This method does not require the number of clusters k as an input, but needs a termination condition Step 0 a b Step 1 Step 2 Step 3 Step 4 ab abcde c cde d de e Step 4 agglomerative (AGNES) Step 3 Step 2 Step 1 Step 0 divisive (DIANA)

AGNES (Agglomerative Nesting) p Implemented in statistical analysis packages, e. g. , Splus p Use the Single-Link method and the dissimilarity matrix. p Merge objects that have the least dissimilarity p Go on in a non-descending fashion p Eventually all objects belong to the same cluster p Single-Link: each time merge the clusters (C 1, C 2) which are connected by the shortest single link of objects, i. e. , minp C 1, q C 2 dist(p, q)

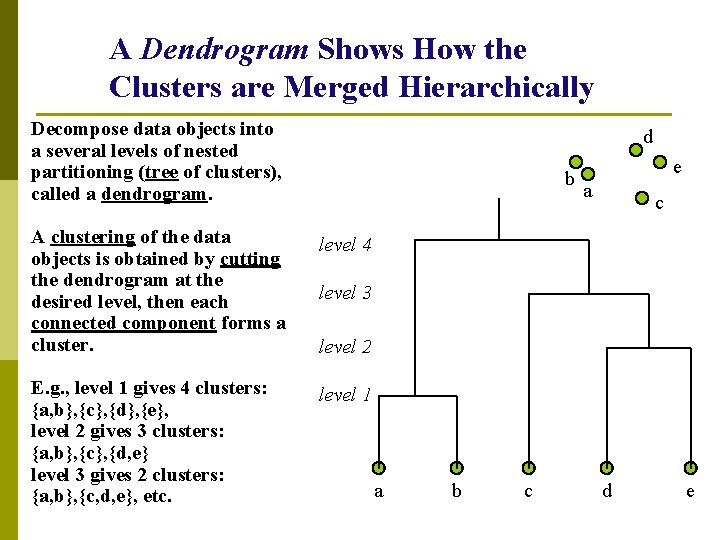
A Dendrogram Shows How the Clusters are Merged Hierarchically Decompose data objects into a several levels of nested partitioning (tree of clusters), called a dendrogram. d b A clustering of the data objects is obtained by cutting the dendrogram at the desired level, then each connected component forms a cluster. level 4 E. g. , level 1 gives 4 clusters: {a, b}, {c}, {d}, {e}, level 2 gives 3 clusters: {a, b}, {c}, {d, e} level 3 gives 2 clusters: {a, b}, {c, d, e}, etc. level 1 e a c level 3 level 2 a b c d e

DIANA (Divisive Analysis) p Implemented in statistical analysis packages, e. g. , Splus p Inverse order of AGNES p Eventually each node forms a cluster on its own

More on Hierarchical Clustering Methods p Major weakness of agglomerative clustering methods n n p do not scale well: time complexity of at least O(n 2), where n is the number of total objects can never undo what was done previously Integration of hierarchical with distance-based clustering n n n BIRCH (1996): uses CF-tree and incrementally adjusts the quality of sub-clusters CURE (1998): selects well-scattered points from the cluster and then shrinks them towards the center of the cluster by a specified fraction CHAMELEON (1999): hierarchical clustering using dynamic modeling

BIRCH (1996) p Birch: Balanced Iterative Reducing and Clustering using Hierarchies, by Zhang, Ramakrishnan, Livny (SIGMOD’ 96) p Incrementally construct a CF (Clustering Feature) tree, a hierarchical data structure for multiphase clustering p n Phase 1: scan DB to build an initial in-memory CF tree (a multi-level compression of the data that tries to preserve the inherent clustering structure of the data) n Phase 2: use an arbitrary clustering algorithm to cluster the leaf nodes of the CF-tree Scales linearly: finds a good clustering with a single scan and improves the quality with a few additional scans

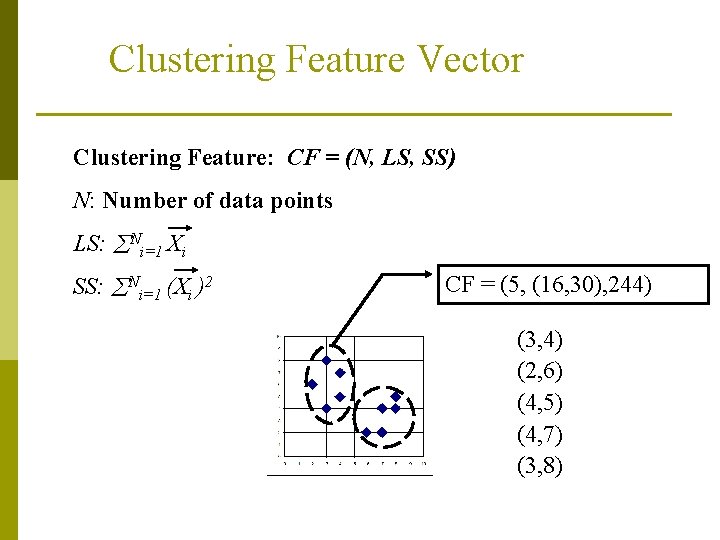
Clustering Feature Vector Clustering Feature: CF = (N, LS, SS) N: Number of data points LS: Ni=1 Xi SS: Ni=1 (Xi )2 CF = (5, (16, 30), 244) (3, 4) (2, 6) (4, 5) (4, 7) (3, 8)

Some Characteristics of CFVs p p Two CFVs can be aggregated. n Given CF 1=(N 1, LS 1, SS 1), CF 2 = (N 2, LS 2, SS 2), n If combined into one cluster, CF=(N 1+N 2, LS 1+LS 2, SS 1+SS 2). The centroid and radius can both be computed from CF. n centroid is the center of the cluster n radius is the average distance between an object and the centroid. Other statistical features as well. . .

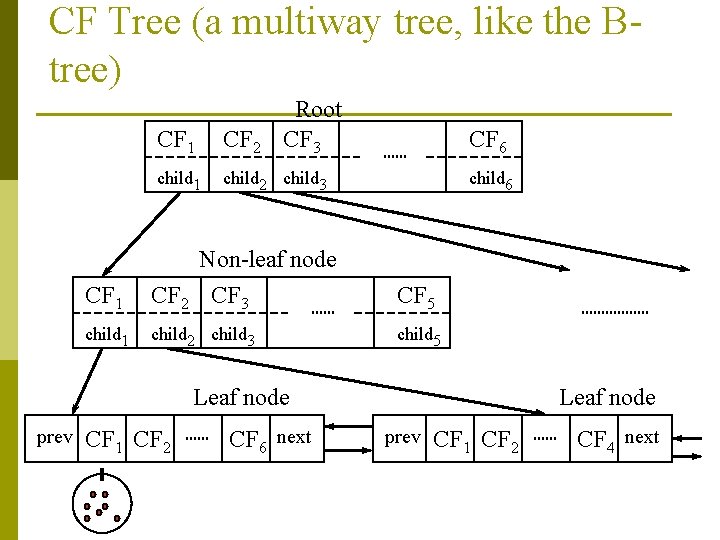
CF-Tree in BIRCH A CF tree is a height-balanced tree that stores the clustering features for a hierarchical clustering p n A nonleaf node in a tree has (at most) B descendants or “children” n The nonleaf nodes store sums of the CFs of their children n A leaf node contains up to L CF entries A CF tree has two parameters n Branching factor B: specify the maximum number of children. n threshold T: max radius of a sub-cluster stored in a leaf node

CF Tree (a multiway tree, like the Btree) Root CF 3 CF 1 CF 2 child 1 child 2 child 3 CF 6 child 6 CF 1 Non-leaf node CF 2 CF 3 CF 5 child 1 child 2 child 3 child 5 Leaf node prev CF 1 CF 2 CF 6 next Leaf node prev CF 1 CF 2 CF 4 next

CF-Tree Construction p Scan through the database once. p For each object, insert into the CF-tree as follows: n At each level, choose the sub-tree whose centroid is closest. n In a leaf page, choose a cluster that can absort it (new radius < T). If no cluster can absorb it, create a new cluster. n Update upper levels.